Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:20:23.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Random affine code tree fractals and Falconer–Sloan condition

Published online by Cambridge University Press:  15 December 2014

ESA JÄRVENPÄÄ ,
MAARIT JÄRVENPÄÄ ,
BING LI  and
ÖRJAN STENFLO
ESA JÄRVENPÄÄ
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected], [email protected]
MAARIT JÄRVENPÄÄ
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected], [email protected]
BING LI
Affiliation:
Department of Mathematical Sciences, PO Box 3000, 90014 University of Oulu, Finland email [email protected], [email protected] Department of Mathematics, South China University of Technology, Guangzhou 510641, PR China email [email protected]
ÖRJAN STENFLO
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, 75106 Uppsala, Sweden email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We calculate the almost sure dimension for a general class of random affine code tree fractals in 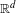$\mathbb{R}^{d}$. The result is based on a probabilistic version of the Falconer–Sloan condition 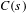$C(s)$ introduced in Falconer and Sloan [Continuity of subadditive pressure for self-affine sets. Real Anal. Exchange 34 (2009), 413–427]. We verify that, in general, systems having a small number of maps do not satisfy condition 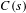$C(s)$. However, there exists a natural number $n$ such that for typical systems the family of all iterates up to level $n$ satisfies condition 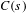$C(s)$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 5 , August 2016 , pp. 1516 - 1533
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. A fractal valued random iteration algorithm and fractal hierarchy. Fractals 13 (2005), 111–146.CrossRefGoogle Scholar
Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. V-variable fractals: fractals with partial self similarity. Adv. Math. 218 (2008), 2051–2088.Google Scholar
Barnsley, M., Hutchinson, J. E. and Stenflo, Ö.. V-variable fractals: dimension results. Forum Math. 24 (2012), 445–470.Google Scholar
Barral, J. and Feng, D.-J.. Multifractal formalism for almost all self-affine measures. Comm. Math. Phys. 318 (2013), 473–504.Google Scholar
Falconer, K. J.. The Hausdorff dimension of self-affine fractals. Math. Proc. Cambridge Philos. Soc. 103 (1988), 339–350.Google Scholar
Falconer, K. J.. Sub-self-similar sets. Trans. Amer. Math. Soc. 347 (1995), 3121–3129.Google Scholar
Falconer, K. J.. Fractal Geometry, 2nd edn. John Wiley, Chichester, 2003.Google Scholar
Falconer, K. J. and Miao, J.. Dimensions of self-affine fractals and multifractals generated by upper triangular matrices. Fractals 15 (2007), 289–299.Google Scholar
Falconer, K. J. and Miao, J.. Random subsets of self-affine fractals. Mathematika 56 (2010), 61–76.Google Scholar
Falconer, K. J. and Sloan, A.. Continuity of subadditive pressure for self-affine sets. Real Anal. Exchange 34 (2009), 413–427.Google Scholar
Feng, D.-J.. Lyapunov exponents for products of matrices and multifractal analysis. Part II: General matrices. Israel J. Math. 170 (2009), 355–394.Google Scholar
Feng, D.-J. and Shmerkin, P.. Non-conformal repellers and the continuity of pressure for matrix cocycles. Geom. Funct. Anal. 24 (2014), 1101–1128.Google Scholar
Järvenpää, E., Järvenpää, M., Käenmäki, A., Koivusalo, H., Stenflo, Ö. and Suomala, V.. Dimensions of random affine code tree fractals. Ergod. Th. & Dynam. Sys. 34 (2014), 854–875.Google Scholar
Jordan, T., Pollicott, M. and Simon, K.. Hausdorff dimension for randomly perturbed self affine attractors. Comm. Math. Phys. 270 (2007), 519–544.CrossRefGoogle Scholar
Käenmäki, A. and Shmerkin, P.. Overlapping self-affine sets of Kakeya type. Ergod. Th. & Dynam. Sys. 29 (2009), 941–965.Google Scholar
Kechris, A.. Classical Descriptive Set Theory. Springer, New York, 1995.CrossRefGoogle Scholar
Mauldin, R. D. and Urbański, M.. Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets (Cambridge Tracts in Mathematics, 148) . Cambridge University Press, Cambridge, 2003.Google Scholar
Przytycki, F. and Urbański, M.. On the Hausdorff dimension of some fractal sets. Studia Math. 93 (1989), 155–186.Google Scholar
Roy, M. and Urbański, M.. Random graph directed Markov systems. Discrete Contin. Dyn. Syst. 30 (2011), 261–298.Google Scholar
Solomyak, B.. Measure and dimensions for some fractal families. Math. Proc. Cambridge Philos. Soc. 124 (1998), 531–546.Google Scholar