Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T04:31:37.246Z Has data issue: false hasContentIssue false
  • English
  • Français

On the entropy of linear factors

Published online by Cambridge University Press:  01 April 2008

BENJAMIN WEISS
BENJAMIN WEISS*
Affiliation:
Hebrew University of Jerusalem, Jerusalem 91904, Israel (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In general, the entropy 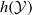of a stationary process 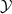, which is a factor of the process 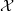, can take any value in the interval 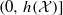. For linear factors the situation is completely different. In fact it even matters how the class of linear factors is defined. We will investigate both moving averages of bounded sequences by coefficients in l1 and the natural notion in L2.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 2: William Parry Memorial Volume , April 2008 , pp. 697 - 705
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Furstenberg, H.. Disjointness in ergodic theory, minimal sets, and a problem in Diophantine approximation. Math. Systems Theory 1 (1967), 1–49.CrossRefGoogle Scholar
[2]Katznelson, Y.. An Introduction to Harmonic Analysis, 3rd edn. Cambridge University Press, Cambridge, 2004.CrossRefGoogle Scholar
[3]Newman, D. J.. Translates are always dense on the half line. Proc. Amer. Math. Soc. 27 (1969), 511–512.Google Scholar
[4]Parry, W.. Entropy and Generators in Ergodic Theory. W. A. Benjamin, Inc., New York, 1969.Google Scholar
[5]Parry, W.. Topics in Ergodic Theory (Cambridge Tracts in Mathematics, 75). Cambridge University Press, Cambridge, 1981.Google Scholar
[6]Wiener, N.. The Fourier Integral and Certain of its Applications. Cambridge University Press, Cambridge, 1933.Google Scholar