Published online by Cambridge University Press: 06 September 2018
In this paper, we define the notion of monic representation for the 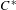 $C^{\ast }$-algebras of finite higher-rank graphs with no sources, and we undertake a comprehensive study of them. Monic representations are the representations that, when restricted to the commutative
$C^{\ast }$-algebras of finite higher-rank graphs with no sources, and we undertake a comprehensive study of them. Monic representations are the representations that, when restricted to the commutative 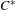 $C^{\ast }$-algebra of the continuous functions on the infinite path space, admit a cyclic vector. We link monic representations to the
$C^{\ast }$-algebra of the continuous functions on the infinite path space, admit a cyclic vector. We link monic representations to the 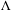 $\unicode[STIX]{x1D6EC}$-semibranching representations previously studied by Farsi, Gillaspy, Kang and Packer (Separable representations, KMS states, and wavelets for higher-rank graphs. J. Math. Anal. Appl. 434 (2015), 241–270) and also provide a universal representation model for non-negative monic representations.
$\unicode[STIX]{x1D6EC}$-semibranching representations previously studied by Farsi, Gillaspy, Kang and Packer (Separable representations, KMS states, and wavelets for higher-rank graphs. J. Math. Anal. Appl. 434 (2015), 241–270) and also provide a universal representation model for non-negative monic representations.