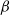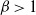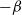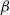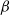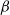Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Masáková, Z.
and
Vávra, T.
2014.
Integers in number systems with positive and negative quadratic Pisot base.
RAIRO - Theoretical Informatics and Applications,
Vol. 48,
Issue. 3,
p.
341.
Akiyama, Shigeki
and
Caalim, Jonathan
2017.
Invariant Measure of Rotational Beta Expansion and Tarski’s Plank Problem.
Discrete & Computational Geometry,
Vol. 57,
Issue. 2,
p.
357.
AKIYAMA, Shigeki
and
CAALIM, Jonathan
2017.
Rotational beta expansion: ergodicity and soficness.
Journal of the Mathematical Society of Japan,
Vol. 69,
Issue. 1,
SUZUKI, Shintaro
2017.
ARTIN-MAZUR ZETA FUNCTIONS OF GENERALIZED BETA-TRANSFORMATIONS.
Kyushu Journal of Mathematics,
Vol. 71,
Issue. 1,
p.
85.