Article contents
Hausdorff dimension of invariant measure of circle diffeomorphisms with a break point
Published online by Cambridge University Press: 07 September 2017
Abstract
We prove that, for almost all irrational 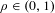 $\unicode[STIX]{x1D70C}\in (0,1)$, the Hausdorff dimension of the invariant measure of a
$\unicode[STIX]{x1D70C}\in (0,1)$, the Hausdorff dimension of the invariant measure of a 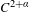 $C^{2+\unicode[STIX]{x1D6FC}}$-smooth
$C^{2+\unicode[STIX]{x1D6FC}}$-smooth 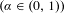 $(\unicode[STIX]{x1D6FC}\in (0,1))$ circle diffeomorphism with a break of size
$(\unicode[STIX]{x1D6FC}\in (0,1))$ circle diffeomorphism with a break of size 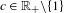 $c\in \mathbb{R}_{+}\backslash \{1\}$, with rotation number
$c\in \mathbb{R}_{+}\backslash \{1\}$, with rotation number  $\unicode[STIX]{x1D70C}$, is zero. This result cannot be extended to all irrational rotation numbers.
$\unicode[STIX]{x1D70C}$, is zero. This result cannot be extended to all irrational rotation numbers.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2017
References
- 7
- Cited by


