Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T04:34:54.028Z Has data issue: false hasContentIssue false
  • English
  • Français

Fundamental domain of invariant sets and applications

Published online by Cambridge University Press:  02 November 2012

PENGFEI ZHANG
PENGFEI ZHANG*
Affiliation:
School of Mathematical Sciences, Peking University, Beijing 100871, China (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 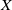$X$ be a compact metric space, 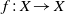$f:X\to X$ a homeomorphism and 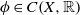$\phi \in C(X,\mathbb {R})$. We construct a fundamental domain for the set of points with finite peaks with respect to the induced cocycle 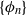$\{\phi _n\}$. As applications, we give sufficient conditions for the transitive set of a non-conservative partially hyperbolic diffeomorphism to have positive Lebesgue measure, i.e., for an accessible partially hyperbolic diffeomorphism, if the set of points with finite peaks for the Jacobian cocycle is not of full volume, then the set of transitive points is of positive volume.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 341 - 352
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Aaronson, J.. An Introduction to Infinite Ergodic Theory (Mathematical Surveys and Monographs, 50). American Mathematical Society, Providence, RI, 1997.Google Scholar
[2]Abdenur, F. and Viana, M.. Flavors of partial hyperbolicity. Preprint, 2008.Google Scholar
[3]Avila, A. and Bochi, J.. Nonuniform hyperbolicity, global dominated splittings and generic properties of volume-preserving diffeomorphisms. Trans. Amer. Math. Soc. 364 (2012), 2883–2907.Google Scholar
[4]Bowen, R.. Topological entropy for noncompact sets. Trans. Amer. Math. Soc. 184 (1973), 125–136.Google Scholar
[5]Burns, K. and Wilkinson, A.. On the ergodicity of partially hyperbolic systems. Ann. of Math. (2) 171 (2010), 451–489.Google Scholar
[6]Burns, K., Dolgopyat, D. and Pesin, Ya.. Partial hyperbolicity, Lyapunov exponents and stable ergodicity. J. Stat. Phys. 108 (2002), 927–942.Google Scholar
[7]Dolgopyat, D. and Wilkinson, A. Stable accessibility is $C^1$ dense. Geometric Methods in Dynamics. II. Astérisque 287 (2003), xvii, 33–60.Google Scholar
[8]Fayad, B. and Katok, A.. Constructions in elliptic dynamics. Ergod. Th. & Dynam. Sys. 24 (2004), 1477–1520.Google Scholar
[9]Gurevic, B. M. and Oseledec, V. I.. Gibbs distributions, and the dissipativity of C-diffeomorphisms. Dokl. Akad. Nauk SSSR 209 (1973), 1021–1023 (Russian); Engl. transl. Soviet Math. Dokl. 14 (1973), 570–573.Google Scholar
[10]Halmos, P.. Invariant measures. Ann. of Math. (2) 48 (1947), 735–754.Google Scholar
[11]Halmos, P.. Lectures on Ergodic Theory. The Mathematical Society of Japan, Tokyo, 1956.Google Scholar
[12]Kaimanovich, V. A.. Hopf decomposition and horospheric limit sets. Ann. Acad. Sci. Fenn. Math. 35 (2010), 335–350.Google Scholar
[13]Pfister, C. E. and Sullivan, W. G.. On the topological entropy of saturated sets. Ergod. Th. & Dynam. Sys. 27 (2007), 929–956.Google Scholar
[14]Rodriguez Hertz, F., Rodriguez Hertz, M. and Ures, R.. A survey of partially hyperbolic dynamics. Partially Hyperbolic Dynamics, Laminations, and Teichmüller Flow, 35–87 (Fields Institute Communications, 51). American Mathematical Society, Providence, RI, 2007.Google Scholar
[15]Sinaǐ, Y.. Markov partitions and $C$-diffeomorphisms. Funct. Anal. Appl. 2 (1968), 61–82.Google Scholar
[16]Xia, Z.. Hyperbolic invariant sets with positive measures. Discrete Contin. Dyn. Syst. 15(3) (2006), 811–818.Google Scholar
[17]Zhang, P.. Partially hyperbolic sets with positive measure and $ACIP$ for partially hyperbolic systems. Discrete Contin. Dyn. Syst. 32 (2012), 1435–1447.Google Scholar