Published online by Cambridge University Press: 10 March 2021
Let G be a finite group, let A be an infinite-dimensional stably finite simple unital C*-algebra, and let
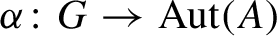 $\alpha \colon G \to {\operatorname {Aut}} (A)$
be an action of G on A which has the weak tracial Rokhlin property. Let
$\alpha \colon G \to {\operatorname {Aut}} (A)$
be an action of G on A which has the weak tracial Rokhlin property. Let
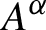 $A^{\alpha }$
be the fixed point algebra. Then the radius of comparison satisfies
$A^{\alpha }$
be the fixed point algebra. Then the radius of comparison satisfies
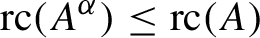 ${\operatorname {rc}} (A^{\alpha }) \leq {\operatorname {rc}} (A)$
and
${\operatorname {rc}} (A^{\alpha }) \leq {\operatorname {rc}} (A)$
and
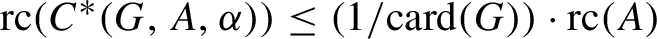 ${\operatorname {rc}} ( C^* (G, A, \alpha ) ) \leq ({1}/{{{\operatorname{card}}} (G))} \cdot {\operatorname {rc}} (A)$
. The inclusion of
${\operatorname {rc}} ( C^* (G, A, \alpha ) ) \leq ({1}/{{{\operatorname{card}}} (G))} \cdot {\operatorname {rc}} (A)$
. The inclusion of
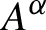 $A^{\alpha }$
in A induces an isomorphism from the purely positive part of the Cuntz semigroup
$A^{\alpha }$
in A induces an isomorphism from the purely positive part of the Cuntz semigroup
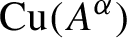 ${\operatorname {Cu}} (A^{\alpha })$
to the fixed points of the purely positive part of
${\operatorname {Cu}} (A^{\alpha })$
to the fixed points of the purely positive part of
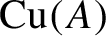 ${\operatorname {Cu}} (A)$
, and the purely positive part of
${\operatorname {Cu}} (A)$
, and the purely positive part of
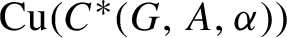 ${\operatorname {Cu}} ( C^* (G, A, \alpha ) )$
is isomorphic to this semigroup. We construct an example in which
${\operatorname {Cu}} ( C^* (G, A, \alpha ) )$
is isomorphic to this semigroup. We construct an example in which
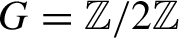 $G \,{=}\, {\mathbb {Z}} / 2 {\mathbb {Z}}$
, A is a simple unital AH algebra,
$G \,{=}\, {\mathbb {Z}} / 2 {\mathbb {Z}}$
, A is a simple unital AH algebra,
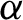 $\alpha $
has the Rokhlin property,
$\alpha $
has the Rokhlin property,
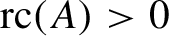 ${\operatorname {rc}} (A)> 0$
,
${\operatorname {rc}} (A)> 0$
,
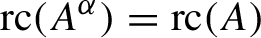 ${\operatorname {rc}} (A^{\alpha }) = {\operatorname {rc}} (A)$
, and
${\operatorname {rc}} (A^{\alpha }) = {\operatorname {rc}} (A)$
, and
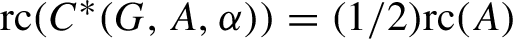 ${\operatorname {rc}} ({C^* (G, A, \alpha)} ) = ({1}/{2}) {\operatorname {rc}} (A)$
.
${\operatorname {rc}} ({C^* (G, A, \alpha)} ) = ({1}/{2}) {\operatorname {rc}} (A)$
.