Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T04:44:36.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Construction of foliations with prescribed separatrix

Published online by Cambridge University Press:  01 June 2008

YOHANN GENZMER
YOHANN GENZMER*
Affiliation:
I.M.T., Université Paul Sabatier 118 Route de Narbonne 31062, Toulouse Cedex, France (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

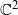A germ of a singular foliation in is built, with its analytical class of separatrix and holonomy representations prescribed. Thanks to this construction, we study the link between the moduli space of a foliation and the moduli space of its separatrix.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 28 , Issue 3 , June 2008 , pp. 817 - 842
Copyright
Copyright © Cambridge University Press 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Berthier, M., Cerveau, D. and Meziani, R.. Transformations isotropes des germes de feuilletages holomorphes. J. Math. Pures Appl. (9) 78(7) (1999), 701–722.CrossRefGoogle Scholar
[2]Camacho, C.. Singularities of holomorphic differential equations. Singularities and Dynamical Systems (Iráklion, 1983) (North-Holland Mathematical Studies, 103). North-Holland, Amsterdam, 1985, pp. 137–159.Google Scholar
[3]Camacho, C. and Movasati, H.. Neighborhoods of Analytic Varieties (Monografías del Instituto de Matemática y Ciencias Afines [Monographs of the Institute of Mathematics and Related Sciences], 35). Instituto de Matemática y Ciencias Afines, IMCA, Lima, 2003.Google Scholar
[4]Camacho, C. and Sad, P.. Invariant varieties through singularities of holomorphic vector fields. Ann. of Math. (2) 115(3) (1982), 579–595.CrossRefGoogle Scholar
[5]Dulac, H.. Recherches sur les point singuliers des équations différentielles. J. Ecole Polytechnique 2 (1904), 1–125.Google Scholar
[6]Godement, R.. Théorie des faisçeaux. Hermann, Paris, 1973.Google Scholar
[7]Lins Neto, A.. Construction of singular holomorphic vector fields and foliations in dimension two. J. Differential Geom. 26(1) (1987), 1–31.Google Scholar
[8]Mattei, J.-F.. Modules de feuilletages holomorphes singuliers. I. Équisingularité. Invent. Math. 103(2) (1991), 297–325.CrossRefGoogle Scholar
[9]Mattei, J. F.. Quasi-homogénéité et équiréductibilité de feuilletages holomorphes en dimension deux. Géométrie complexe et systèmes dynamiques (Orsay, 1995). Astérisque 261(xix) (2000), 253–276.Google Scholar
[10]Mattei, J.-F. and Moussu, R.. Holonomie et intégrales premières. Ann. Sci. École Norm. Sup. (4) 13(4) (1980), 469–523.CrossRefGoogle Scholar
[11]Mattei, J.-F. and Salem, E.. Modules formels locaux de feuilletages holomorphes. Preprint, 2004. arXiv:math/0402256.Google Scholar
[12]Seguy, M.. Cobordismes et reliabilités équisinbulières de singularités marquées de feuilletages holomorphes en dimension deux. PhD Thesis, Toulouse, 2003.Google Scholar
[13]Seidenberg, A.. Reduction of singularities of the differential equation A dy=B dx. Amer. J. Math. 90 (1968), 248–269.CrossRefGoogle Scholar
[14]Spivak, M.. A Comprehensive Introduction to Differential Geometry. Publish or Perish Inc., Boston, MA, 1975.Google Scholar
[15]Zariski, O.. Le problème des modules pour les branches planes, 2nd edn. Hermann, Paris, 1986 (Course given at the Centre de Mathématiques de l’École Polytechnique, Paris, October–November 1973).Google Scholar