Regression approaches in the test-negative study design for assessment of influenza vaccine effectiveness

Summary

Influenza vaccination is the most practical means available for preventing influenza virus infection and is widely used in many countries. Because vaccine components and circulating strains frequently change, it is important to continually monitor vaccine effectiveness (VE). The test-negative design is frequently used to estimate VE. In this design, patients meeting the same clinical case definition are recruited and tested for influenza; those who test positive are the cases and those who test negative form the comparison group. When determining VE in these studies, the typical approach has been to use logistic regression, adjusting for potential confounders. Because vaccine coverage and influenza incidence change throughout the season, time is included among these confounders. While most studies use unconditional logistic regression, adjusting for time, an alternative approach is to use conditional logistic regression, matching on time. Here, we used simulation data to examine the potential for both regression approaches to permit accurate and robust estimates of VE. In situations where vaccine coverage changed during the influenza season, the conditional model and unconditional models adjusting for categorical week and using a spline function for week provided more accurate estimates. We illustrated the two approaches on data from a test-negative study of influenza VE against hospitalization in children in Hong Kong which resulted in the conditional logistic regression model providing the best fit to the data.

INTRODUCTION

Influenza vaccines are unique in requiring annual vaccination for continued protection. The reasons for this are twofold. First, their composition is frequently updated to keep pace with antigenic drift; and second, vaccine-induced immunity rapidly wanes [1]. Moreover, the dominant strain, timing and severity of seasons vary. As a result, the influenza vaccine's effectiveness (VE) may not be constant across seasons and therefore there may be a need for re-estimation each season.

While randomized controlled trials provide the most robust estimates of the efficacy of influenza vaccines, they are not feasible on an annual basis. In contrast, observational studies can easily provide ongoing estimates of influenza VE. Commonly, this is done using data collected through routine surveillance and analysed as a test-negative design study [2]. Using this design, the odds of influenza positivity among the vaccinated are compared to the odds of positivity among the unvaccinated to estimate VE [3].

Although vaccination campaigns are typically timed to precede the start of the influenza season, in some instances the timing of vaccine receipt has overlapped with enrolment; e.g. during the 2009 influenza A(H1N1) pandemic [4]. Thus, both vaccination coverage and influenza incidence can change throughout a season, so time acts as a confounder and should be adjusted for in VE estimation. This is typically achieved by including it as a covariate in a multivariable logistic regression model fitted using unconditional maximum likelihood. The specification of time can vary and it has been included as a continuous variable, a categorical variable or spline function, and the unit of time has also varied [2]. An alternative approach is to use time as a matching variable, which is equivalent to stratification over time, and fit the model using conditional maximum likelihood.

The objective of this paper was to evaluate the validity of the unconditional and conditional maximum-likelihood estimates when applied to data from test-negative studies under different scenarios of influenza vaccination coverage within a season. In the following sections, we provide a detailed description of the test-negative design and the regression approaches considered, and we then present a comparison of approaches using a simulation study and empirical data from a test-negative study conducted in Hong Kong.

Test-negative design

The test-negative design was first used for the estimation of influenza VE in 2005 [5] and has since been used in over 100 papers reporting VE estimates [2]. It is popular because it can take advantage of routine surveillance systems that are already in place in many settings. In these studies, participants meeting a clinical case definition for influenza-like illness or acute respiratory illness are enrolled in a clinical setting, such as an outpatient clinic or a hospital. For example, such a study might recruit patients presenting to their general practitioner (GP) with fever and cough. A respiratory specimen is collected from each participant and tested for influenza virus. Participants meeting the clinical case definition and testing positive for influenza are the cases, while those meeting the clinical case definition and testing negative for influenza are the comparison group. Information on the vaccination status and important confounders is recorded. VE is estimated by comparing the odds of positivity between the vaccinated and unvaccinated; i.e. VE = (1 – OR_adj) × 100, where OR_adj is the odds ratio with correction for potential bias caused by confounding [2, 3, 6].

In contrast to traditional case-control studies, the participant's status (test-positive vs. test-negative) is not known at enrolment, so no sampling frame is used to select participants. Furthermore, all patients are seeking care for the same complaint. This approach is said to avoid the validity issues identified in more traditional case-control studies of influenza VE, which are threatened by bias associated with underlying differences in health status [7] and healthcare-seeking behaviour [3] between vaccinated and unvaccinated patients. By enrolling all patients from the same population, presenting with the same complaint and therefore believed to have similar health status and healthcare-seeking behaviours, this type of bias should be reduced.

A number of assumptions are required for the test-negative design to provide accurate estimates of influenza VE. First, the occurrence of influenza-like illnesses due to non-influenza causes cannot be affected by receipt of influenza vaccine. Second, the test used to determine influenza status must be highly specific, although this is true for any study where the exposure is uncommon [8]. Recruitment should also be restricted to the period during which influenza is circulating.

Motivating example

In a test-negative study of influenza VE, our effect of interest is vaccination on influenza infection. This effect may be confounded by age because both vaccination coverage and risk of infection commonly vary by age. Calendar time might also confound the effect because of its association with the timing of vaccination and the varying probability of infection due to influenza circulation following the seasonal pattern of increase, peak and decline. To account for the potential confounding caused by calendar time, most influenza VE studies include it as a covariate (e.g. week of presentation) in their logistic regression models [2]. However, it is unclear whether simply including a variable in a maximum-likelihood model can sufficiently account for the bias that arises if the vaccination coverage changes over the season. Control for the effects of time may be better handled by using time as a matching variable and estimating VE by conditional maximum likelihood. In such a study, patients are selected for the study by matching cases and controls on time (risk-set sampling). In case-control studies, matching alone does not remove the confounding bias and induces selection bias [9, 10]. To overcome this bias, adjustment for the matching variable is required, which can be achieved by sparse data methods, such as conditional logistic regression [9, 10].

METHODS

Maximum-likelihood estimation of VE in the test-negative design

Adjusted odds ratios to estimate VE are typically calculated using a logistic regression model, which is generally defined by:

(1) $${\rm logit}\;{\rm Pr}(Y = 1 \vert x) = \alpha + \beta ^{\prime}x,$$

where Y is the outcome status of the patients, α is the parameter for the intercept, β is a vector of parameters (β ₁, β ₂, …, β _p ) for the covariates, and x is a vector of covariates. In a study of influenza VE, Y would be the patients' influenza status and the covariates might include vaccination status, age and time.

The parameters in the logistic regression model are estimated by maximum-likelihood estimation, which involves finding the set of parameters for which the probability of the observed data is greatest. Formal likelihood theory is explained in detail in Breslow & Day [11]. Briefly, there are two options: unconditional and conditional.

The unconditional maximum likelihood is described by:

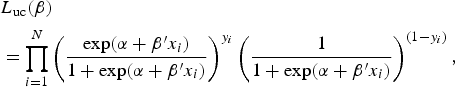(2) $$\eqalign{&{L_{{\rm uc}} (\beta ) }\cr& = \prod\limits_{i = 1}^N \left( {\displaystyle{{\exp (\alpha + \beta ^{\prime}x_i )} \over {1 + \exp (\alpha + \beta ^{\prime}x_i )}}} \right)^{y_i} \left( {\displaystyle{1 \over {1 + \exp (\alpha + \beta ^{\prime}x_i )}}} \right)^{(1 - y_i )},} $$

where N is the total number of individuals.

The conditional maximum likelihood is described by:

(3) $$L_{{\rm con}} (\beta ) = \displaystyle{{\prod\nolimits_{i = 1}^{n_1} {\exp (\beta ^{\prime}x_i )}} \over {\sum\nolimits_k {\prod\nolimits_{i = 1}^{n_1} {\exp (\beta ^{\prime}x_{k_i} )}}}}, $$

where subjects 1 to n ₁ correspond to the cases and n ₀ is the number of controls. The sum in the denominator ranges over the $\left( {\matrix{ n \cr {n_1} \cr}} \right)$ choices of n ₁ integers from the set {1, 2, …, n} [11] for each of k strata.

The conditional likelihood for each stratum is obtained as the probability of the observed data conditional on the stratum total and the number of cases observed:

(4) $$\pi _k (x) = \displaystyle{{\exp (\alpha _k + \beta ^{\prime}x_i )} \over {1 + \exp (\alpha _k + \beta ^{\prime}x)}},$$

where α _k represents the contribution of all constant terms, including the matching variables, within the kth stratum [12].

The two maximum-likelihood estimates differ in some important ways. The conditional estimate does not equal the unconditional estimate and has no explicit formula [12]. Nevertheless, the interpretation of the regression coefficients is the same. Moreover, the conditional estimate is always closer to the null and tends to be less biased than the unconditional estimate [11, 10]. However, when samples are large, the two likelihood estimates and their standard errors will be asymptotically identical [13].

For the test-negative design study, where time is a covariate, the logistic regression model corresponds to:

(5) $${\rm logit}\;{\rm P}(I = 1 \vert v,a,c) = \alpha + \beta _1 v + \beta _2 a + \beta _3 c,$$

where v represents vaccination, a age and c calendar time. Conversely, when patients are matched on time, the model is:

(6) $${\rm logit}\;{\rm P}(I = 1 \vert v,a)_k = \alpha _k + \beta _1 v + \beta _2 a,$$

where there are k = 1, 2, …, n strata of calendar time.

Simulation study

To begin the investigation a simple discrete time simulation using three vaccination scenarios was performed: (1) all vaccinations administered before the epidemic; (2) vaccinations administered before and during the epidemic; (3) vaccinations administered throughout the peak period of the epidemic at a constant rate. (The period of 13 weeks was chosen as the peak period based on sentinel surveillance data from Australia, which indicated that the epidemic period was approximately 13 weeks) [14, 15]. The three scenarios are illustrated in Figure 1.

Fig. 1. Plots showing the epidemic curve and the number of vaccinated patients using the three different vaccination scenarios. Solid black lines show the infected susceptibles, dashed black lines show the infections among vaccinated persons and the grey lines show the total vaccine coverage. We assume vaccines become effective 2 weeks after vaccination.

The simulated population size was 1 million people. VE was set at 60%, based on a recent meta-analysis [16]. The proportion vaccinated π was set to 0·3 based on the prevalence of vaccination among test-negative subjects in some recent outpatient studies [17–20]. The proportion infected with influenza ψ was set to 0·05 [21]. The rate of infection for other respiratory viruses γ was set to 0·3 [22]. Additionally, the proportions of those infected with influenza which were selected to be in the test-negative dataset ψ _S and other viruses selected to be in the test-negative dataset γ _S were arbitrarily set to 0·005. These parameters are summarized in Table 1. The simulation model assumes restricted age to avoid incorporating a statistical adjustment for age.

Table 1. Parameters used in the simulation

Epidemic curves were produced using a binomial (25, 0·5) infection pattern (P) to populate the numbers of infected susceptibles (S _I=1), infected vaccinees (V _I=1), susceptibles infected with other, non-influenza viruses (S _O=1) and vaccinees infected with non-influenza viruses (V _O=1) using the following equations:

(7) $$\eqalign{& S_{I = 1} = S \times \psi \times {\rm P}, \cr & V_{I = 1} = V \times \psi \times {\rm P} \times (1 - {\rm VE}), \cr & S_{O = 1} = S \times \gamma \times ({\rm P} \pm {\rm lag}), \cr & V_{O = 1} = V \times \gamma \times ({\rm P} \pm {\rm lag}).} \Bigg \} $$

Susceptibles and vaccinees infected with non-influenza viruses followed the same epidemic curve as those with influenza. However, the peak of the epidemic curve was varied to occur 2 or 6 weeks before and 2 or 6 weeks after the peak of the influenza epidemic. The main analysis here shows the case in which the non-influenza viruses occur 2 weeks before. The model was restricted to run only during the epidemic period, defined as the weeks in which there were ⩾1 patients testing positive for influenza, as this is a commonly used criterion [2]. Sensitivity analyses were carried out to assess: the sensitivity of parameter inputs to the simulation results by varying the expected VE, proportion vaccinated and proportion testing positive; the effect of running the model outside of the epidemic period (i.e. not restricting to the data to weeks with cases); and the effect of differing the onset time of the non-influenza viruses epidemic.

Each simulation was run 1000 times. Five regression models were assessed: (1) crude logistic regression (L); (2) logistic regression with week as a continuous variable (LW); (3) logistic regression with week as a categorical variable (LC); (4) logistic regression with week as a restricted cubic spline function with four knots (LS); (5) conditional logistic regression, stratified by week (CL).

Application to test-negative data from Hong Kong

The use of conditional logistic regression was compared with ordinary logistic regression using data from a test-negative study conducted in Hong Kong [23]. Children were enrolled on a specified day each week from the paediatric inpatient wards of two large public hospitals on Hong Kong island – Queen Mary Hospital and Pamela Youde Nethersole Eastern Hospital. Inclusion criteria were: (1) resident of Hong Kong island; (2) aged 2–5 years; (3) meeting the case definition of a febrile acute respiratory infection, defined as fever ⩾38 °C with any respiratory symptom such as cough, runny nose, or sore throat. Respiratory specimens were collected from all enrolled children and tested for influenza by immunofluorescence, culture, and/or reverse transcription–polymerase chain reaction. Influenza vaccination history within 6 months of hospitalization was elicited from the parents or legal guardians of enrolled patients using a standardized questionnaire administered by research staff. The methods have been described in detail previously [6]. VE was estimated using the same regression models described for the simulation study, excluding the crude logistic regression model as we a priori believe that time should be adjusted. Age was restricted to avoid including it in the regression models.

RESULTS

Simulation study

For the simulation study, results for VE using the previously mentioned models are shown in Table 2. These results suggest that when all vaccinations are administered before the epidemic, adjusting a regression model for time is not necessary as the crude model gives a VE estimate close to our set parameter value of 60%. The results show slight bias in the crude model for scenario 2 where all vaccinations are given before and during the epidemic. Larger biases were observed in the crude model for scenario 3 where vaccinations are given at a constant rate during the epidemic. These simulation results therefore suggest that if modelling a situation in which vaccinations are being administered during an epidemic adjusting for time in a regression model is necessary. How this adjustment is made, however, seems to have little effect on the results.

Table 2. Vaccine effectiveness (VE) and 95% sampling intervals obtained from simulated results using conditional and unconditional maximum-likelihood models under three vaccination scenarios

SI, Sampling interval; L, crude model; LW, adjusting for week as a continuous variable; LC, adjusting for week as a categorical variable; LS, adjusting for week with a spline term; CL, conditional logistic model matching on week.

Sensitivity analysis was also carried out to inspect the sensitivity of the simulation towards parameter values. Figure 2 shows the differences when we restrict the model to only run during the influenza season (⩾1 positive case each week) and when we allow the model to run on all data. We expected there to be bias when using the entire surveillance period vs. just the weeks with cases because this is what has been seen in practice [24]. However, the two panels in Figure 2 show minimal differences. Such variability is probably a product of sample size, such that in a study with a small overall sample, changing the definition of the study period can have a severe impact on VE estimates. In contrast, our simulated datasets included between 1000 and 2000 patients, which may have been sufficient to overcome sampling problems.

Fig. 2. Plots showing results of the sensitivity analysis comparing calculated vaccine effectiveness estimates when data are restricted to the influenza epidemic period vs. using entire surveillance period. Data shown are point estimates and sampling intervals for each model.

The effect of varying parameter values is shown in Figure 3. These adjustments have little effect on the calculated VE estimate, except when the probability of infection (PI) is increased in which case the sampling intervals for the estimate narrow. Again, there is evidence of bias towards the null in the crude estimate obtained from scenarios 2 and 3.

Fig. 3. Plots showing the sensitivity analysis performed using different combinations of parameter values. VE, Vaccine effectiveness; PV, proportion vaccinated; PI, proportion infected. Data shown are point estimates and sampling intervals for each model.

We also conducted a sensitivity analysis, examining the effect of varying the onset of the epidemic curves for non-influenza viruses. This was done by implementing the non-influenza viruses' curves with a 2- and 6-week lag and a 2- and 6-week lead/advance. The infection pattern for both influenza and non-influenza viruses were the same throughout the analysis [binomial (25, 0·5)]. The results are shown in Table 3. We can see that when the two epidemic curves are significantly separated, i.e. 6 weeks lag and 6 weeks lead, the bias shown for the crude model in scenarios 2 and 3 is large. This analysis also shows that when the non-influenza epidemic occurs before the influenza epidemic the crude model underestimates VE and, conversely, when this occurs after the influenza epidemic the crude model overestimates VE. This highlights the need for time adjustment in a model where the vaccination is given during the influenza epidemic especially when the non-influenza virus activity occurs before or after the influenza epidemic. We can also see slight bias in all models when the difference between the influenza and other virus' epidemics are greatest.

Table 3. Sensitivity analysis showing the effects of differing the epidemic period for non-influenza viruses. Values shown in table are VE (%) with 95% sampling intervals

L, crude model; LW, adjusting for week as a continuous variable; LC, adjusting for week as a categorical variable; LS, adjusting for week with a spline term; CL, conditional logistic model matching on week.

Overall, considering all simulation results, including the sensitivity analyses, it is shown that when vaccinations are distributed during an epidemic the models producing the most accurate results are the logistic model adjusting for time as a categorical variable or using a spline function, and the conditional logistic regression model matching on time.

Application to test-negative data from Hong Kong

Between 1 October 2009 and 30 September 2013, 2467 children were recruited from the inpatient departments of two hospitals, of whom 241 (9·8%) tested positive for influenza A virus and 82 (3·3%) tested positive for influenza B virus. The timeline of recruitment of patients is shown in Figure 4. The upper panel shows that influenza virus infections in Hong Kong occurred throughout the year, with occasional peaks and troughs in incidence. Elsewhere we have shown that peaks in influenza virus activity tend to occur in winter (February–March) and summer (June–July) in subtropical Hong Kong although the seasonal pattern can vary from year to year [6, 25].

Fig. 4. Enrolment of patients and vaccination coverage over calendar time in Hong Kong. (a) Number of enrolled children each week, by laboratory test result. The dark grey bars show the test-negative patients and the light grey bars show the test-positive patients. (b) Vaccine coverage among cases testing negative for influenza virus, smoothed using the Daniel 1 kernel [26].

The lower panel of Figure 4 shows the influenza vaccination coverage among the test-negative patients, which reflects vaccination coverage in the population, varied throughout each year, with highest coverage between January and March each year. Hong Kong uses the Northern Hemisphere influenza vaccine and vaccination campaigns typically run from October to January prior to the winter influenza season, although vaccines are also administered at other times of the year and are available throughout the year.

From analysis of the hospital data we found among the test-negative patients, 245/(1899 + 245) (11·4%) reported receipt of influenza vaccination in the preceding 6 months, compared to 18/(305 + 18) (5·6%) of patients that tested positive for influenza A or B virus. Estimates of the VE adjusted for different time indicators were estimated from fitting conditional and unconditional maximum-likelihood models (Table 4).

Table 4. Estimated vaccine effectiveness (VE) under alternative regression models

CI, Confidence interval; AIC, Akaike's Information Criterion; LW, adjusting for week as a continuous variable; LC, adjusting for week as a categorical variable; LS, adjusting for week with a spline term; CL, conditional logistic model matching on week.

* Weeks without a case and a non-case were dropped from models 2 and 4.

Table 4 shows the results from the unconditional logistic regression models adjusting for time in the previously described ways and the conditional logistic model using matched time variables. Among the unconditional models, Akaike's Information Criterion (AIC) values indicated that the model including a categorical variable for week was the preferred model; however, the model including a spline function for week provided similar estimates and AIC values. However, the AIC value for the conditional model was lower, suggesting this approach fit the data best. The models were run using differing units of time (i.e. week, month, 12-week period). When the unit of time was 12 weeks no weeks were dropped in the conditional regression or the model with categorical time, and therefore the sample size included in the conditional regression was the same as the sample included in all the unconditional models allowing for a fair comparison of AIC values. This comparison still shows the AIC to be the lowest in the conditional model. Regardless of the unit of time, the conditional model shows the lowest AIC, concluding that this model fitted the data the best. Each model, with the exception of the continuous unconditional model (which stayed consistent across all time indicators), provided a better fit with the smaller unit of time (week).

DISCUSSION

Based on the analysis presented here, the need to adjust for time depends on which scenario best fits the data under study. Scenario 1 may best represent a typical, temperate season, where the majority have been vaccinated prior to the start of the epidemic. On the other hand, scenario 2 may be more realistic in seasons where the epidemic starts early, or where seasons closely follow or even coincide with vaccine availability, which may occur in some regions [27–30] or during pandemics [4]. However, we conservatively recommend that either the conditional logistic model, or an unconditional model in which week is included either as a categorical variable or using a spline function may be the most appropriate models to use for a test-negative data set. As well as producing accurate estimates for the simulation data under a range of scenarios, these models also permitted reliable estimation of VE in the Hong Kong hospital data. Although not seen in the simulation or Hong Kong application here, the conditional logistic model has been shown to produce slightly larger standard errors than the logistic model due to a higher number of parameters needed for the conditional logistic regression model resulting in greater uncertainty [11]. However, the reduced bias may be preferable to reduced precision.

One limitation of our approach is that we did not consider the impact of potential confounding variables on the estimation of VE. An important confounder of this relationship is age, which we attempted to control the effects of by restricting the analysis to children aged 2–5 years. However, we did not explore how adjustment for this variable might influence estimates. This would be one area for further work, perhaps with an agent-based simulation model. Further to this, we did not explore effect modification across levels of this confounder. However, we note that in practice most published datasets may have insufficient sample to adequately explore effect modification. Gains in understanding how an effect varies across levels of covariates must be weighed against other potential biases. For example, inclusion of product terms can overparameterize the model and lead to sparse data bias, the severity of which may be greater than confounding bias [31–33]. Second, for the application to clinical data, the true VE is unknown and we cannot be sure that the regression models we used were able to account sufficiently for confounding. In practice, matching on calendar time may be more useful in tropical regions, like Hong Kong, where there may be multiple influenza seasons within a year; conversely in temperate climates where the influenza season typically follows a neat epidemic curve and where most patients will have been vaccinated prior to the epidemic, the need to control for time may be reduced.