INTRODUCTION
Tick-borne encephalitis (TBE) is the most serious flavivirus infection in temperate Eurasia [Reference Mansfield1]. It is a classic obligatorily transmissible zoonosis where the causative virus (TBEV) circulates among vector ticks and their vertebrate hosts in natural ecosystems independently of humans, who can acquire the disease only if accidentally exposed to infected ticks (or, more rarely, consume milk of viraemic animals). Several pathways of virus circulation in nature have been identified including transovarial transmission from an infected female tick to her offspring, reciprocal transmission from an infectious host to non-infected ticks and vice versa via a blood route (systemic or viraemic transmission), and direct exchange of the virus between infectious and non-infected ticks feeding close together on a non-infectious host (co-feeding or non-viraemic transmission). According to a current paradigm, it is the latter mechanism that actually perpetuates the virus in nature [Reference Labuda2]. Between 1990 and 2012, over 65 500 cases of TBE were reported in 18 European countries [Reference Kunze3]. Permanent sequelae occur in 2–10% patients, and the case-fatality rate in Europe is 0·5–2·0% [Reference Dumpis, Crook and Oksi4]. No curative treatment is available, and good understanding of the disease epidemiology is of great importance for organizing the disease's prophylaxis [Reference Heinz5].
A typical feature of TBE epidemiology is the profound fluctuation in annual case numbers. Causes are sought within long-term variation in factors within the zoonotic system, as well as in variable human exposure to the disease foci. Remarkably, although ticks (mainly Ixodes ricinus and I. persulcatus) are the principal vectors of TBEV and are even regarded as its main reservoir [Reference Labuda and Randolph6], only a weak correlation was detected between fluctuations in TBE incidence and tick population density or virus prevalence in ticks in longitudinal studies [Reference Korenberg and Kovalevskii7, Reference Süss8].
However, the factor that was shown to be correlated with human disease is the population density of animal hosts and/or their tick load. A crucial role – both as a source of nourishment for immature ticks and as ‘bridge hosts’ for the virus – is attributed to small rodents (mainly Apodemus spp. and Myodes spp.). The morbidity and/or mortality of TBE was repeatedly demonstrated to be correlated with their 1-year lagged population density [Reference Okulova9, Reference Zeman and Benes10]. A long-term monitoring of small mammals showed that TBE outbursts in the human population were preceded by periods of increased TBE seroprevalence and heightened tick load in the micromammal population 1–2 years earlier; it is hypothesized that the increases in morbidity in particular years were due to higher virulence of TBEV strains which the vector ticks had acquired via viraemic transmission from rodents [Reference Moshkin11].
Population dynamics of some medium-sized and large mammals was also occasionally reported to be correlated with TBE. Deer are another vital bloodmeal source for tick populations; however, ruminants are considered non-competent hosts for TBEV transmission, and inconsistent findings regarding the relationship between TBE incidence and deer population estimates can be found in the literature [Reference Palo12–Reference Knap and Avsic-Zupanc14]. A paradoxical inverse relationship was observed between TBE and hare or grouse population density [Reference Palo12]. Several published models include carnivore (red fox, mink) population data as a predictor for TBE incidence: obviously, these species are closely linked to populations of the host species through their predator–prey relationships [Reference Palo12, Reference Kiffner13, Reference Haemig15].
There is a general consensus that climate is the primary driver of TBE fluctuations. However, attempts to find a clear-cut correlation were mostly without notable success [12, 13; as opposed to 9, 15]. Some authors find environmental factors insufficient to explain all TBE fluctuations: for example, human behavioural responses to weather – rather than weather-induced variation in the zoonotic system itself – were proposed as an explanation of an abnormal morbidity peak which occurred synchronously in various parts of Europe in 2006 [Reference Randolph16].
An analysis of TBE incidence in Austria, Slovenia, and the Czech Republic revealed marked similarities in consecutive rises and falls in case numbers in these countries of central Europe (CE) [Reference Heinz5]. In this study, historical data on TBE morbidity in CE are re-analysed. The aim was to characterize in a rigorous way mutual coherencies in incidence series within this highly endemic region, and to improve the predictive understanding of TBE fluctuations.
METHODS
Area and data
Altogether six incidence series, spanning from 1971 to 1974 to 2013, and representative of the CE endemic zone (European TBEV subtype transmitted by I. ricinus), were included in this study.
Austria, Slovenia, and the Czech Republic. The incidence series originated in consistent passive surveillance systems as explained in [Reference Heinz5]. For Austria, where the vaccination coverage is well documented, TBE incidence was calculated relative to the non-vaccinated sub-population; in the other countries, vaccination was disregarded.
Bavaria and Baden-Württemberg. In Germany, TBE cases have been compulsorily notifiable since 2001 [17], earlier data originated from active surveillance launched in 1974 [Reference Roggendorf and Süss18, Reference Süss19].
Switzerland. TBE incidence series was compiled from several sources combining active and passive (from 1984 on) surveillance data [Reference De Marval20–22].
Data on the populations of the different countries were obtained from the national offices of statistics.
Study design
Fluctuations in TBE data could equally likely reflect variations in zoonotic risk, in the rate of human contact with it, as well as in the efficacy of the surveillance and reporting of the disease; there are three main types of time-related patterns potentially present in such data: time clustering, periodic patterns, and longitudinal trends [Reference Rothman, Greenland and Lash23]. The main objective of this analysis was to reveal the hidden periodicities. These could be attributed to cyclic or recurring processes in the zoonotic system, whereas long-term changes in human exposure or disease reporting are, as a rule, non-periodic in nature.
To this end, any trend – i.e. a long-term change in the mean incidence – was first removed from the data. This eliminated most of the effects of human exposure, vaccination, disease reporting, etc. which are region/country-specific. Second, for each of the de-trended incidence series, a power spectrum was estimated. The spectrum decomposed the total time-series variance into contributions from individual frequencies, thus cycles of differing length could be identified. Third, oscillatory dynamics – i.e. how the phase and amplitude of each cycle changes over time – was analysed and compared across CE.
Methods employed
The incidence series were ‘stationarized’ (i.e. modified to remove the trend and stabilize variance) utilizing the empirical mode decomposition (EMD) method [Reference Huang24]. To detect oscillations in the series, power spectra were estimated using a modification of Welch's overlapped segment averaging method [Reference Schulz and Mudelsee25]. Continuous wavelet (CW) transformation was applied to convert the one-dimensional incidence series into their two-dimensional time-frequency representations which made it possible to trace how the detected oscillations varied in time [Reference Torrence and Compo26]. Finally, a multivariate synchrosqueezing method (MSS) was used to identify oscillations common to the six series [Reference Ahrabian27].
Statistical significance
It was argued that the ‘coloured-noise’ null hypothesis is ill-fitted for testing the significance of periodicities in epidemiological time series – therefore, the so-called ‘beta-surrogate’ null model (H0) was utilized throughout this study as a more appropriate alternative [Reference Cazelles, Cazelles and Chavez28].
Software
EMD calculations were made using the module EMD v. 1.5.7 under R (https:// www.r-project.org/). Power spectra were computed using the program REDFIT v. 3.5 (http://www.geo.uni-bremen.de/geomod/staff/mschulz/software/redfit35.zip). CW transformation was performed using the package WAVEPACK (http://paos.colorado.edu/research/wavelets/). MSS analysis was done utilizing the package MULTIVARIATE_SST (http://www.commsp.ee.ic.ac.uk/~mandic/research/Multivariate_SST_code.zip). The programs were modified to implement the ‘beta-surrogate’ model.
RESULTS
Correlation analysis
Raw incidence series exhibit marked variation across CE [panel (a) in Figs 1–6]. After de-trending [panel (b) in Figs 1–6] , the data revealed a meaningful pattern of distance-decaying correlations: generally, the series in adjacent areas tend to be correlated more closely with each other than those in geographically more distant areas. In addition, the transformed series also show a similar autocorrelation pattern which indicates that TBE maxima and minima in CE alternate approximately every 5 years on average (Fig. 7).

Fig. 1. Tick-borne encephalitis dynamics in the Czech Republic: (a) raw incidence series with the trend superimposed; (b) de-trended and standardized series; (c) continuous wavelet (CW) spectrum showing the time evolution of different periodicities whose amplitude is grey-tone coded [see the top right scale bar; note that the amplitudes within a year ‘sum’ to (b)], the white dashed line delimits the ‘cone of influence’ – a sector within which the spectrogram is free of edge effects; (d) power spectrum of the de-trended series with the respective (left to right) 80%, 90%, and 95% confidence limits (based on 1000 Monte Carlo simulations of H0). Note that the diagram shows four dominant periodicities – of ~2·5, 3, 5, and 10 years – with at least 80% confidence levels; to focus the eye, they are traced across the CW spectrum by horizontal lines.

Fig. 2. Tick-borne encephalitis dynamics in Austria. Details as in Figure 1 legend.

Fig. 3. Tick-borne encephalitis dynamics in Slovenia. Details as in Figure 1 legend.

Fig. 4. Tick-borne encephalitis dynamics in Bavaria. Details as in Figure 1 legend.

Fig. 5. Tick-borne encephalitis dynamics in Baden-Württemberg. Details as in Figure 1 legend.

Fig. 6. Tick-borne encephalitis dynamics in Switzerland. Details as in Figure 1 legend.
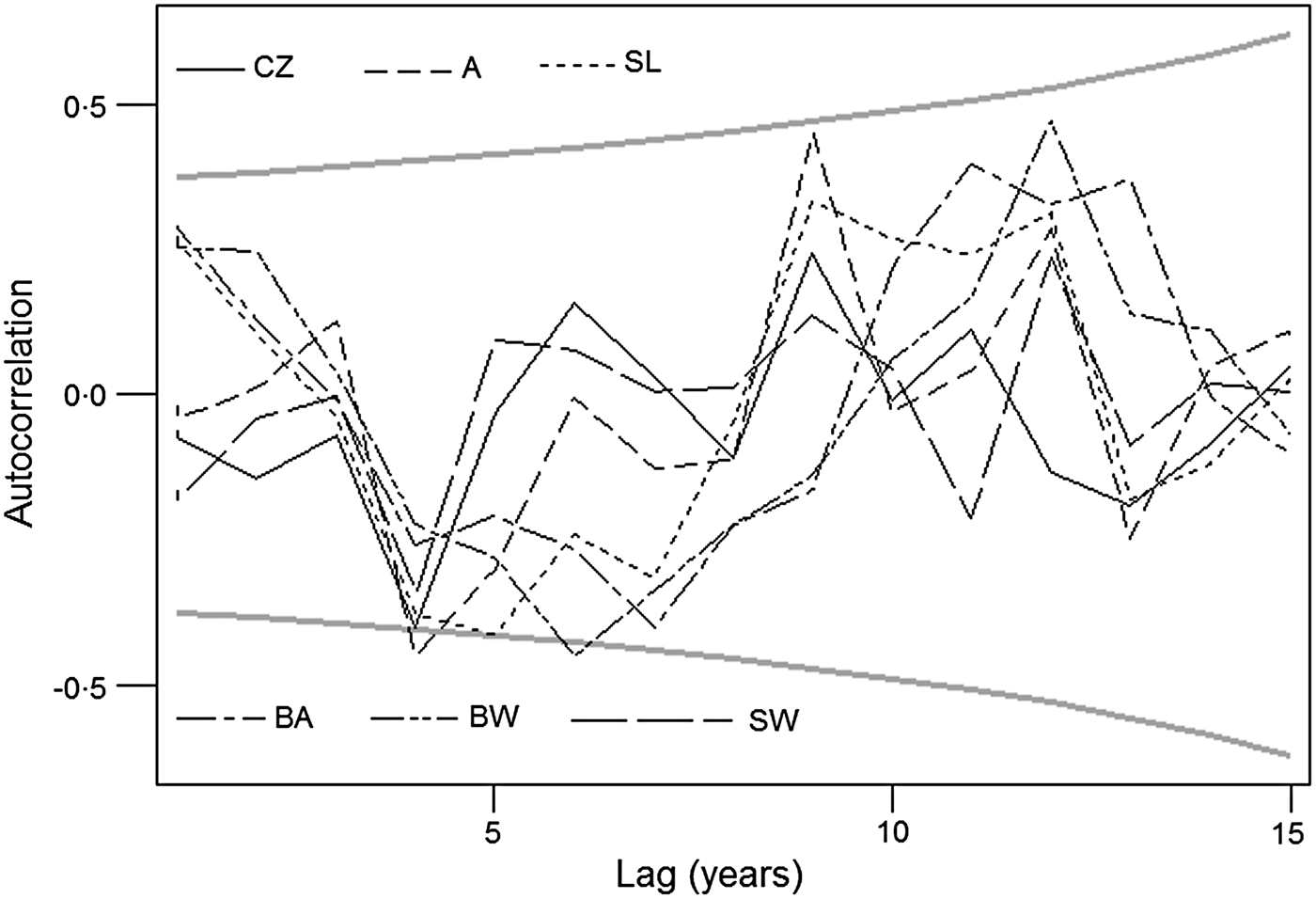
Fig. 7. Autocorrelation of the six de-trended tick-borne encephalitis incidence series; 95% confidence limits of randomness are shown in grey. Note that maxima and minima of the disease incidence alternate about every 5 years (range ~4–7 years). CZ, Czech Republic; A, Austria; SL, Slovenia; BA, Bavaria: BW, Baden-Württemberg; SW, Switzerland.
Spectral analysis
Power spectra are shown in panel (d) of Figures 1–6; four distinct cycles – about 2·5, 3, 5, and 10 years long, respectively – can be identified. The cycles are disproportionately pronounced in different areas: the most prominent one is the quasi-10-year cycle which dominates (P > 0·95) the oscillations in all areas except Switzerland (P < 0·8). It apparently corresponds with the above alternations of long-term TBE maxima and minima detected by autocorrelation analysis. Estimates of the cycle's length vary between 9–12 years (mean 10·75 years). The second most prominent cycle is the ~3-year cycle (2·8–3, mean 2·9 years), it is dominant in Switzerland (P > 0·95), well pronounced in Austria, Slovenia, and the Czech Republic (P ⩾ 0·95), but insignificant in Bavaria and Baden-Württemberg (P≈0·8). The shortest, ~2·5-yr cycle (2·3–2·5, mean 2·4 years) is most strongly pronounced in Switzerland (P > 0·95), manifest in Austria and the Czech Republic (P ⩽ 0·9), but weak in the other areas (P < 0·8). The quasi-5-year cycle (5·2–5·7, mean 5·5 years) is clearly detectable in the Czech Republic (P = 0·95) and Bavaria (P < 0·9), visible but insignificant in Slovenia and Switzerland (P ⩽ 0·8), and difficult to identify in Austria and Baden-Württemberg.
CW spectra of the de-trended series are shown in panel (c) of Figures 1–6; they document that the observed TBE fluctuations can be adequately explained in terms of superposition of the four basic oscillations. The differential admixture proportions as well as amplitude and slight phase variations of these (quasi-periodic) oscillations could clearly account for regional differences in the incidence series. For example, most countries/lands in CE experienced a more-or-less distinct period of elevated incidence in the early 1990s which can be associated with a culmination of the quasi-10-year cycle in around 1994. No such elevation was registered in Switzerland where this particular oscillation was low in intensity. Nevertheless, the oscillation's intensity in this country gradually increased afterwards so that it gained significance in the early 2000s (Fig. 6c , Supplementary Fig. S1). An opposite trend, i.e. a decline in the quasi-10-year oscillation after the 1994 maximum, is seen in the Czech Republic (Fig. 1c . Supplementary Fig. S1). The analysis gives an uninvolved explanation of abrupt TBE outbursts such as that observed in 2006; they obviously correspond with coinciding maxima of multiple oscillations, especially of the 2·5- and 3-year cycles. For example, the prominent 2006 peak in the Czech Republic is apparently a result of the culmination of the 2·5-, 3- and 5-year cycles coinciding (Fig. 1). Eventually, a slight phase shift in the oscillations can explain the fact that, in Austria and Bavaria, the disease peaked a year before, in 2005, and that the 1979 peak was delayed until 1982 (Figs 2 and 4).
Synchronization analysis
The output of the MSS analysis is shown in Fig. 8; it distinguishes four common oscillations of the respective cycle lengths of about 2·5, 3·2, 5·3, and 10·5 years, clearly matching the four cycle constituents of TBE fluctuations identified by spectral analysis. Although a certain phase variance is apparent, the common oscillations exhibit a relatively high degree of synchrony across CE. For example, within the period of observation, 10 out of the total of 14 ~3-yr cycles had the same timing both in the Czech Republic and Switzerland (Figs 1c and 6c ). The most prominent ~10-year cycle culminated almost uniformly in all countries/lands between 1994 and 1995, and the ~5-year cycle exhibited a period of complete synchrony in about 2003 in all areas where recorded. Additionally, MSS analysis as well as CW spectra document periodic changes in the degree of synchrony in the regional oscillations (an alignment of the CW spectra is provided in Supplementary Fig. S2). It can be best illustrated with the 2·5- and ~3-year cycles: marked in-phase periods (around 1981, 1994, and 2006) alternate with rather off-phase periods, which is suggestive of some ‘synchronizing impulses’ with a period of ~14 years (10–16, mean 13·5 years) in the background.
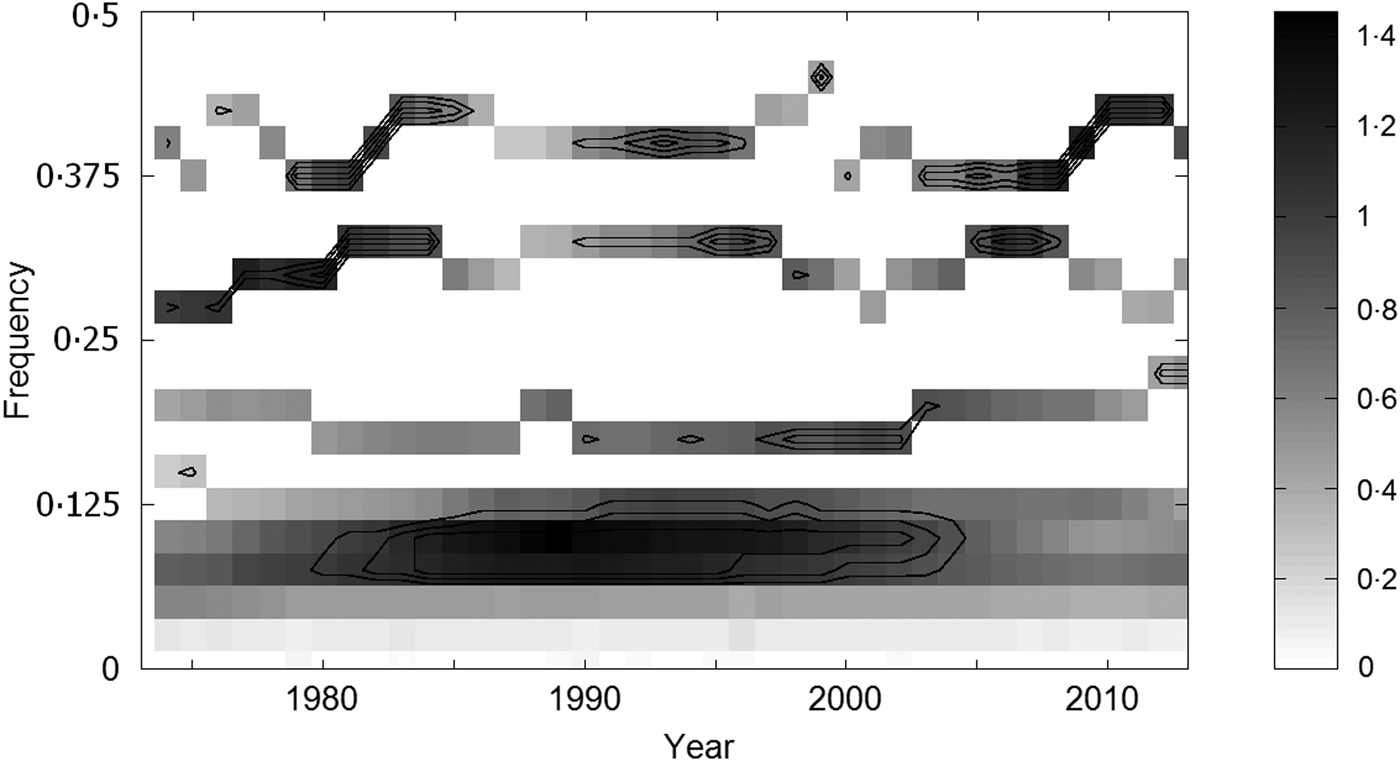
Fig. 8. Time-frequency (multivariate synchrosqueezing method) localization of the oscillations which the six regional tick-borne encephalitis incidence series exhibit in common; grey tones correspond to the degree to which the oscillations are synchronized, and the concentric lines indicate the respective (from outer to inner) 80%, 90%, and 95% levels at which randomness can be excluded (based on 100 (×6) Monte Carlo simulations of the series under H0). Note four bands – common oscillations of the wavelengths varying around 2·5, 3·2, 5·3, and 10·5 years, respectively.
DISCUSSION
The question as to whether the unstable dynamics of transmissible disease is determined by external (e.g. climatic) factors, self-oscillations of the disease system itself, or is a result of the joint action of external and internal mechanisms, is an unsolved issue [Reference Martcheva, Prosper, Rao and Durvasula29]. The patterns of TBE detected in CE seem to correspond best with the third alternative, although external forcing appears to dominate. The moments of phase synchrony, interlaced among relatively asynchronous periods, can be explained by the varying preponderance of one driving mechanism over the other, and the ‘synchronizing impulses’ identified with power maxima in the external signal. The self-oscillations may arise in (delayed) feedback loops within the disease system (e.g. immunity level in a host population responds to the amount of circulating virus which, in turn, responds to the immunity level; abundance of predators influences that of the hosts, which, in turn, influences the predators, etc.). They may be synchronized by some external periodic perturbation (e.g. global climatic oscillations) through the system's spontaneous self-organization [Reference Janson30].
The manifold of oscillations composing TBE dynamics clearly reflects the complexity of the disease system. While it cannot be resolved with certainty to what extent individual determinants of the zoonotic risk (i.e. tick population density, virus prevalence and/or amount in ticks, virulence of circulating strains, etc.) contribute to each particular oscillation, the frequency of these oscillations notably correspond to periodicity (rhythmicity) of the population dynamics of key hosts and the vector tick itself. I. ricinus – subject to climatic conditions and host availability – adapts its developmental cycle so that it can include one or more diapauses potentially prolonging its length up to ~6 years [Reference Gray31, Reference Randolph, Bowman and Nuttall32]. Under central European conditions, ontogeny of each developmental stage typically lasts 1 year; in a minor part of the population, it is prolonged to 1·5–2 years, and occasionally it is completed within <1 year. Given the ⩾1-year mean interval between successive feedings, the 2·5-year cycle corresponds with twice this interval, and could be explained in terms of a process encompassing two successive feedings, for example, as resulting from the feedback loop between quantity of the virus transmitted by the ith tick generation and host immunity induced by feeding of the i – 1th generation. Possible synchronization impulses could be produced by the quasi-biennial (~28-month) climate cycle (QBO), or the quasi-biennial components of the El Niño Southern Oscillation and/or North Atlantic Oscillation, which influence weather over the Northern Hemisphere.
The main hosts of pre-imaginal stages of I. ricinus – essential to sustaining TBEV circulation in nature – are murid rodents (in CE, primarily Myodes glareolus and Apodemus flavicollis). Adult individuals of these species (males in particular) bear the highest tick burden in the host population, and are estimated to support ⩾75% of all TBEV transmissions [Reference Moshkin11, Reference Kiffner13]. The average lifespan of these animals – estimated to be 1 year – circumscribes the immune memory of the host population, and harmonizes with the ~1-year mean interval between tick feedings; both in conjunction clearly account for a feedback loop with quasi-biennial periodicity. Another characteristic feature of the population dynamics of small rodents is a tendency to fluctuate between scarcity and abundance in more-or-less regular multi-annual cycles [Reference Finerty33]. In CE, rodent populations typically peak every 3 years (range 2–5 years). The cycles are synchronous over large areas; possible inducing factors include plant/seed production, predation, and meteorological conditions, e.g. snow cover. The detailed mechanisms are, however, not fully understood as yet. Interestingly, a collation of 71 time-series of vole population density across the Czech Republic (time window 1968–1988) showed a period of enhanced synchrony between 1976 and 1983, preceded and followed by relative asynchrony [Reference Tkadlec34] – a pattern exactly matching that in the TBE series (cf. Fig. 8, Supplementary Fig. S2). Thus, cycling of background rodent population levels seem to underlie the quasi-triennial TBE oscillation.
The most prominent ~10-year TBE oscillation can be readily associated with the conspicuous quasi-decadal population cycle of various large and medium-sized herbivores (e.g. deer, hares) and also some insectivores, carnivores and birds (e.g. hedgehog, lynx, grouse) over the Northern Hemisphere [Reference Keith35]. Most of these species are important tick food sources, and their abundance directly regulates tick population density. The quasi-decadal ‘wildlife’ cycle is notably regular and synchronous over wide geographical areas. The underlying mechanisms are under dispute; nevertheless, the extensive spatial synchrony is suggestive of exogenous forcing (‘Moran effect’); implicated factors include climatic and even some extraterrestrial (lunar, solar) cycles [Reference Selas36].
The ~5-year TBE oscillation is the most enigmatic. Its explanation may lie in a mechanism halving the dominant ~10-year cycle. Another explanation is that some host species, relevant in some areas, follow a quasi-pentennial population cycle which propagates into the TBE incidence. Finally, it should be noted that – while weak in CE – the ~5-year TBE oscillation may be dominant elsewhere: distinctly 5- to 6-year-spaced TBE outbursts were reported from some regions in the Far East [Reference Leonova37]. A clear-cut 5-year cycle (along with a 10-year cycle) was also distinguished in the population dynamics of I. persulcatus in East Siberia [Reference Korotkov38]. Inducing factors of the quasi-pentennial fluctuations could thus be multiple and various.
In summary, this analysis showed that the ostensibly chaotic fluctuations in TBE risk in CE can be explained in terms of several superposed (quasi-)periodical oscillations which themselves exhibit recurrent rises and falls in synchrony. It is proposed that the cyclic TBE patterns arise as basically diverging self-oscillations of local disease systems. At intervals, they receive synchronizing impulses, such as periodic variations in food availability for key hosts driven by some external factors [Reference Ostfeld39]. This leads to synchronization of the disease dynamics over a large area at peaks of the synchronization signal, and shifting to asynchrony during the time in between. The degree of synchrony is thus contingent on both the intensity and duration of the synchronizing impulses, as well as on the locally specific composition of host synusia and corresponding pathogen–vector–host interactions. This insight into the cyclic patterns of TBE may permit forecasting of the risk several years ahead even if details of the underlying enzootic processes remain concealed at present. Further research and a better comprehension of the underlying natural as well as human-driven factors, could make TBE fluctuations reasonably predictable.
SUPPLEMENTARY MATERIAL
For supplementary material accompanying this paper visit http://dx.doi.org/10.1017/S0950268816002223.
DECLARATION OF INTEREST
None.










