1. Introduction
The United Nations Conference on Climate Change in Cancún in 2010 (COP16) and in Durban in 2011 (COP17) adopted a new approach to designing international environmental agreements (IEAs) compared to the previous Kyoto framework. This new emerging post-Kyoto framework combines the efforts of emissions abatement with adaptation. While most climate experts agree that abatement and adaptation are the two main options available to tackle climate change, unfortunately, the role of adaptation is largely ignored in the study of IEAs.Footnote 1 In this paper, we focus on the role of adaptation in the incentives to join a coalition. In particular, we study how cross-country differences in adaptation costs affect the incentives to join an IEA.
Adaptation refers to any activity with a potential to reduce the damages from climate change. For example, the construction of dams, levees or dikes, changing the types of crops used in agriculture or improving storm predictions and their warnings (Parry, Reference Parry2007). The World Bank (2011) estimates that an approximate 2°C increase in world temperatures by 2050 may require between US $ 70 and US $ 100 bn a year in adaptation costs from 2010 to 2050.Footnote 2 These adaptation costs differ widely across countries. For instance, studies find evidence of cost differences between developed and developing countries (World Bank, 2010). In addition, adaptation efforts also affect country-level mitigation.Footnote 3 For example, in many developing countries, agroforestry helps farmers adapt to climate change while also helping country-level mitigation through carbon sequestration (Verchot et al., Reference Verchot, Van Noordwijk and Kandji2007; Kristjanson et al., Reference Kristjanson, Neufeldt and Gassner2012; Mbow et al., Reference Mbow, Smith, Skole, Duguma and Bustamante2014).Footnote 4 Thus, these cross-country differences in adaptation costs and the relationships between emissions and adaptation yield new challenges in understanding countries' incentives to join climate coalitions.
Our main goal is to study how the possibility to adapt to climate change affects countries' incentives to emit and to join an IEA. To do so, we first study how a country's emissions respond to their own higher adaptation effort and how a country's emissions respond to lower emissions by other countries. Next, we analyze how cross-country differences in adaptation costs can affect these strategic relationships and the incentives to join a coalition. We address these issues within the framework of IEA membership games first introduced by Carraro and Siniscalco (Reference Carraro and Siniscalco1993) and Barrett (Reference Barrett1994). In contrast to the previous literature, we explicitly model the possibility of adaptation, in addition to emissions abatement, to reduce environmental damages.
We introduce three modeling features that differentiate our paper from previous work. First, countries can simultaneously choose emissions and adaptation levels. In our context, the most important feature that distinguishes emissions and adaptation decisions relates to their public and private good nature. While each country's emissions generate a private benefit, their damages have the nature of a global public bad. However, this is distinct from adaptation. While adaptation also generates a private benefit, its costs only affect the individual country. Therefore, in our setting, a key feature is that emissions abatement has an international public good nature, while adaptation has a national private good nature.
Next, we account for cross-country differences in adaptation costs. This feature addresses some of the concerns raised in the recent climatic negotiations since Cancún in 2010 (COP16) and Durban in 2011 (COP17), where the importance of adaptation differences between developed and developing countries for environmental agreements was first highlighted. For example, the Cancún Adaptation Fund, established in 2010, aims at reducing the technological gap that exists between developed and developing countries. Thus, in our model, we assume the existence of two types of countries: countries with low adaptation costs and countries with high adaptation costs.
The third modeling feature that distinguishes our work from others is that we consider a general damage function that can be both linear and non-linear. By doing so, we are able to show that the existence of carbon leakage, a country's response to lower emissions by other countries, is determined by adaptation costs.Footnote 5
We define a country's payoff as the difference between benefits from emissions and the sum of environmental damages and adaptation costs. Each country's production activities generate a global pollutant that benefits each country privately while simultaneously damaging all countries. A country can offset these damages by choosing individual adaptation levels. We capture the expenditure in adaptation with an increasing cost function. Then countries simultaneously choose emission and adaptation levels that maximize their own payoff given others' strategies.
Within this context we derive several results. First, we find that reducing the adaptation cost disparity between countries leads to higher global emissions. Secondly, the strategic relationship between emissions and adaptation effort depends on adaptation costs. Moreover, an exogenous reduction in adaptation costs can switch a substitutable relationship between emissions and adaptation to a complementary relationship. We also find that the existence of carbon leakage is determined by adaptation costs and that only some countries have carbon leakage when cost heterogeneity is large. Furthermore, an exogenous reduction in cost disparity between countries can eliminate carbon leakage.
In the membership game, we find that the presence of adaptation is not necessarily a destabilizing factor in coalition formation. This is in contrast to the view that putting efforts towards adaptation will discourage participation in IEAs. Finally, we find that a country's incentives to join a coalition depend on how a country responds to its own adaptation and how a country responds to others' higher emissions. Since these two effects depend on adaptation costs, an exogenous reduction in adaptation costs can change the incentives to emit and join a coalition. These findings imply that policies directed at reducing the gap in adaptation costs, such as the Cancún adaptation fund, or policies directed at reducing carbon leakage, such as the Clean Development Mechanism, can help reduce the adaptation burden for less developed countries, but they might also strengthen or weaken the incentives for large environmental agreements.
Our paper closely relates to two main strands of the literature: the literature studying the strategic relationship between emissions abatement and adaptation to climate change, and the literature studying the incentives to form IEAs. A main goal of the first strand of the literature is to understand how a country's incentives to emit respond to a higher adaptation effort by the same country. Kane and Shogren (Reference Kane and Shogren2000) examine the optimal mix of the two measures in a one-country model, while Onuma and Arino (Reference Onuma and Arino2011) investigate how innovation in adaptation technology by a developed country may affect a developing country through changes in abatement efforts by both countries. Some studies analyze the n-country case. Buob and Stephan (Reference Buob and Stephan2008, Reference Buob and Stephan2011) develop a multi-region model where countries choose abatement and adaptation non-cooperatively.Footnote 6 Zehaie (Reference Zehaie2009) studies the importance of the timing between adaptation and emissions, and Ebert and Welsch (Reference Ebert and Welsch2012) study the interactions between emissions and adaptation in a two-country model. Our work differs from these papers because we study the incentives to join IEAs and the role of cost heterogeneity in addition to the strategic relationship between emissions abatement and adaptation effort.
The second strand of the literature is extensive and studies the incentives to join IEAs and the stability of those agreements. Finus (Reference Finus2003) provides a detailed review of this literature.Footnote 7 However, a common feature of these studies is that they ignore the possibility to adapt to climate change. Our paper contributes to this broader literature as it is among the first to study adaptation possibilities within the context of IEAs. By doing so, we identify that the incentives to join IEAs directly depend on adaptation costs which present new challenges to the success and failure of IEAs. We are only aware of a few studies directly analyzing adaptation possibilities in the context of IEAs. Benchekroun et al. (Reference Benchekroun, Marrouch and Ray Chaudhuri2011) study the effect of an improvement in adaptation technologies on free-riding incentives, while Marrouch and Ray Chaudhuri (Reference Marrouch and Ray Chaudhuri2011) focus on the impact of adaptation possibilities on the stable size of IEAs. Our paper differs from these two papers in that we analyse cross-country differences in adaptation costs. This enables us to identify how these differences in adaptation costs can encourage or discourage incentives to emit and join IEAs.
The remainder of the paper unfolds as follows. In section 2 we present a model with heterogeneous adaptation costs. In section 3 we present the non-cooperative and cooperative cases, while section 4 analyzes the strategic relationships between emission and adaptation levels and the existence of carbon leakage. In section 5 we examine coalition formation and the stability of IEAs. Finally, section 6 concludes.
2. Model: emissions game with adaptation
We consider an n-country model where each country emits a global pollutant as a result of its consumption and production activities. We let e
i
denote the emission level of country i where i ∈ N = {1,2, …,n}, and
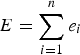 $E=\sum_{i=1}^{n}e_{i}$
are total emissions. While total emissions damage all countries, each country can offset the negative effects of pollution by abating and/or investing in adaptation. Let a
i
denote the adaptation level of country i, which we think of as the flow of effective adaptation that reflects both the level of the adaptation effort and the efficiency of the adaptation technology. The key difference between emissions and adaptation lies in the international nature of pollution and the national nature of adaptation.Footnote
8
While each country's emissions are a private decision, pollution is a global public bad that creates free-riding incentives on emissions abatement. Instead, adaptation is a private decision with country-specific benefits and costs. This distinction between the public and the private nature of emissions and adaptation is key to understanding each country's incentives to choose emissions abatement.
$E=\sum_{i=1}^{n}e_{i}$
are total emissions. While total emissions damage all countries, each country can offset the negative effects of pollution by abating and/or investing in adaptation. Let a
i
denote the adaptation level of country i, which we think of as the flow of effective adaptation that reflects both the level of the adaptation effort and the efficiency of the adaptation technology. The key difference between emissions and adaptation lies in the international nature of pollution and the national nature of adaptation.Footnote
8
While each country's emissions are a private decision, pollution is a global public bad that creates free-riding incentives on emissions abatement. Instead, adaptation is a private decision with country-specific benefits and costs. This distinction between the public and the private nature of emissions and adaptation is key to understanding each country's incentives to choose emissions abatement.
Each country's welfare (i.e., payoff) consists of benefits from polluting activities, emission damages and adaptation costs. Global pollution damages all countries equally, while each has the option to reduce damages through adaptation. In our model, the only source of heterogeneity between countries is the difference in adaptation costs.Footnote 9
We first consider a benefit function that is identical across countries. Country i's benefit from polluting is:
where α and β are positive parameters.Footnote 10 The concave functional form of this benefit function is convenient to restrict the maximum level of benefits from emissions. All countries benefit equally from emissions, which implies the same production technology across countries.Footnote 11
Next, the damage function for country i is:
where ω > 0 is a damage parameter from total pollution.Footnote
12
We do not allow for over-adaptation by assuming that ω is larger than effective adaptation, i.e., ω > a
i
.Footnote
13
Parameter η ≥ 1 captures the curvature of the damage function including the commonly used linear and quadratic damage functions. We highlight three characteristics of equation (2). First, the marginal damage from emissions,
![]() $\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial e_{i}}}=\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial E}}=\lpar \omega -a_{i}\rpar E^{\eta -1}\geq 0\comma \; $
is decreasing in adaptation a
i
. Secondly, a country's damage decreases in its level of adaptation,
$\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial e_{i}}}=\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial E}}=\lpar \omega -a_{i}\rpar E^{\eta -1}\geq 0\comma \; $
is decreasing in adaptation a
i
. Secondly, a country's damage decreases in its level of adaptation,
![]() $\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial a_{i}}}=\displaystyle{{-E^{\eta}}\over{\eta}}\leq 0$
. Thirdly, the marginal benefit from adaptation is increasing in total emissions,
$\displaystyle{{\partial D\lpar E\comma \; a_{i}\rpar }\over{\partial a_{i}}}=\displaystyle{{-E^{\eta}}\over{\eta}}\leq 0$
. Thirdly, the marginal benefit from adaptation is increasing in total emissions,
![]() $\displaystyle{{\partial ^{2}D\lpar E\comma \; a_{i}\rpar }\over{\partial a_{i}\partial E}}=-E^{\eta -1}\leq 0$
.
$\displaystyle{{\partial ^{2}D\lpar E\comma \; a_{i}\rpar }\over{\partial a_{i}\partial E}}=-E^{\eta -1}\leq 0$
.
The final component of a country's payoff is the adaptation cost:
where c j is the cost parameter for high (H) and low (L) adaptation cost countries. A novel feature of our model is that we consider cross-country differences in adaptation costs by allowing countries to be identical within each group but to differ across groups. Let n H and n L denote the number of each type such that they add up to the total number of countries, n = n L + n H . Equation (3) features diminishing returns to scale in the level of adaptation.
We combine these three elements in (1)–(3) to define country i's payoff as:
Having defined the payoff function, we analyse the polar cases in the next section.
3. Non-cooperation and full cooperation
In this section we analyse the non-cooperative and cooperative emission strategies where each country chooses emission and adaptation levels simultaneously.Footnote 14 These polar cases are used as a benchmark and to identify the strategic relationships between variables in section 4. They also clarify the stability analysis in section 5 because non-signatory and signatory countries behave like non-cooperative and cooperative countries, respectively. In the following, we derive the non-cooperative outcome.
3.1. Non-cooperation
Country i simultaneously chooses emission and adaptation levels that maximize its own payoff, taking as given all other countries' choices.Footnote 15 Formally, country i solves:
where W (a i , e i , E) is given by (4). In the subsequent sections, nc and c represent the non-cooperative and cooperative cases. The first-order conditions for emissions (e i ) and adaptation effort (a i ) are:
Equation (6) indicates that the marginal benefits of emissions must equal the adaptation-adjusted marginal damage from polluting in equilibrium. It also shows how a country's adaptation reduces the marginal damage from global emissions. Meanwhile, condition (7) states the equality between the marginal benefit and the marginal cost of adaptation. As shown in (7), a country's choice of adaptation depends on global emissions and its own costs.Footnote 16 In addition, condition (7) suggests that countries with a low cost of adaptation choose to adapt more than countries with a high cost of adaptation. The possibility to adapt to climate change differentiates these conditions from the well-known optimality conditions in a pure IEA membership game. Finally, condition βc j + (η-1) (ω-a j ) c j E η-2 - E 2 (η - 1) <0 satisfies the second-order condition which helps identify the direction of the strategic relationships between variables in section 4.
From (6) and (7), we derive the implicit best-response functions that depend on global emissions. Then, substituting the implicit adaptation function into the implicit best-response function yields individual emissions as a function of global emissions:
 $$e_{nc}^{j} = \displaystyle{{1}\over{\beta}}\left(\alpha +\displaystyle{{E_{nc}^{2\eta-1}}\over{\eta c^j}}- \omega E_{nc}^{\eta-1}\right)\comma \; \quad j=L\comma \; H. $$
$$e_{nc}^{j} = \displaystyle{{1}\over{\beta}}\left(\alpha +\displaystyle{{E_{nc}^{2\eta-1}}\over{\eta c^j}}- \omega E_{nc}^{\eta-1}\right)\comma \; \quad j=L\comma \; H. $$
Finally, using (8), and the fact that E nc = n L e nc L + n H e nc H when group symmetry is applied, yields:
 $$\eta\lpar \beta E_{nc}-n\alpha\rpar = E_{nc}^{\eta-1}\left[-n \eta \omega+\left(\displaystyle{{n^L}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^H}}\right)E_{nc}^{\eta}\right].$$
$$\eta\lpar \beta E_{nc}-n\alpha\rpar = E_{nc}^{\eta-1}\left[-n \eta \omega+\left(\displaystyle{{n^L}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^H}}\right)E_{nc}^{\eta}\right].$$
From this equation we can solve for the non-cooperative level of total emissions E nc and therefore, given (6) and (7), we can also solve for the emission and adaptation levels of the non-cooperative equilibrium.
3.2. Full cooperation
All countries choose emission and adaptation levels that maximize the joint payoff. Formally:
 $$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in N}}\sum_{i=1}^{n}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar \comma \; $$
$$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in N}}\sum_{i=1}^{n}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar \comma \; $$
where W(a i ,e i ,E) is given by (4). The first-order conditions for emissions and adaptation effort are:
Equation (11) indicates that the marginal benefit from individual emissions equals the sum of all marginal damages from pollution minus the adaptation level.Footnote 17 Since adaptation is a private decision, equation (12) states that the private marginal benefit and the private marginal cost from adaptation must be equal, as is the case in the non-cooperative case. The second-order conditions for a maximum are given by c L (n H )2 + c H (n L )2 < c H c L β. From equations (11) and (12) we derive the implicit best-response function. Then, by substituting adaptation into this equation, we obtain:
 $$e_{c}^{j}=\displaystyle{{1}\over{\beta}}\left[\alpha -\left(n\omega -\displaystyle{{E_{c}^{\eta}}\over{\eta}}\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)\right)E_{c}^{\eta -1}\right]\comma \; \quad j=L\comma \; H. $$
$$e_{c}^{j}=\displaystyle{{1}\over{\beta}}\left[\alpha -\left(n\omega -\displaystyle{{E_{c}^{\eta}}\over{\eta}}\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)\right)E_{c}^{\eta -1}\right]\comma \; \quad j=L\comma \; H. $$
Note that equation (13) is identical for low and high adaptation cost countries. This shows that all countries emit the same amount in equilibrium even though they differ in adaptation costs. This is so because countries jointly maximize their payoffs and they fully internalize the negative global externality. Thus, in the full cooperative case, the only difference between low and high adaptation cost countries is given by their adaptation level in (12). As expected, low-cost countries always adapt more than high-cost countries.
Using equation (13) and E c = n L e c L + n H e c H , we derive:
 $$\eta \lpar \beta E_c-n\alpha \rpar = n E_c^{\eta-1} \left[-n \eta \omega+\left(\displaystyle{{n^L}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^H}}\right)E{_c}^{\eta} \right]. $$
$$\eta \lpar \beta E_c-n\alpha \rpar = n E_c^{\eta-1} \left[-n \eta \omega+\left(\displaystyle{{n^L}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^H}}\right)E{_c}^{\eta} \right]. $$
At the aggregate level, total emissions are the positive root of (14). These calculations allow us to fully characterize the emission and adaptation levels of the cooperative case.
In appendix A, we present the formal comparison between total emissions under non- and full cooperation.Footnote 18 Recall that, in the absence of adaptation, full cooperation always leads to lower total emissions than no agreement because countries internalize the negative externality of polluting. As shown in appendix A, this result also holds when we account for adaptation. Specifically, this result is driven by our non over-adaptation assumption. Since each country is unable to over-adapt to climate change, their adaptation-adjusted marginal damage from polluting is higher under full cooperation than non-cooperation (see equations (6) and (11)). This is so because countries under cooperation do not only take into account the marginal damage from pollution in their countries, but also in other countries. Therefore, full cooperative countries internalize the pollution externality, which leads to lower total emissions in equilibrium, even when they are able to adapt to climate change.
Before we turn to analysing the strategic relationships between variables, we look at how the disparity in adaptation costs affects global emissions. We summarize our finding for the linear case in result 1. In the non-linear case, this relationship is more complicated and depends on the magnitudes of variables.
Result 1.
An exogenous reduction in the adaptation cost gap between countries leads to higher global emissions when damages are linear.
To see this, from equations (9) and (14), we obtain total emissions for non and full cooperation in the linear damage case:
 $$E_{nc} = \displaystyle{{n\lpar \alpha -\omega \rpar }\over{\beta -\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}\comma \; $$
$$E_{nc} = \displaystyle{{n\lpar \alpha -\omega \rpar }\over{\beta -\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}\comma \; $$
 $$E_{c} = \displaystyle{{n\lpar \alpha -n\omega \rpar }\over{\beta -n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}\comma \; $$
$$E_{c} = \displaystyle{{n\lpar \alpha -n\omega \rpar }\over{\beta -n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}\comma \; $$
which depend on adaptation costs. Moreover, the optimality conditions (7) and (12) show that a country's adaptation effort increases as adaptation costs get smaller. Higher adaptation efforts in turn lead to higher individual and global emissions in the linear case.Footnote 19 With this in mind, we consider an exogenous change in the cost of adaptation (c). The first example considers a reduction in adaptation costs for high-cost countries, say as a response to a global policy to reduce the cost gap between countries. In the second example, we consider a reduction in adaptation costs for low-cost countries, say as a response to exogenous technological improvements in adaptation. We derive the effect of these two examples in global emissions from equations (15) and (16). In both examples, as adaptation costs get cheaper for some countries, they respond by increasing their adaptation effort. This in turn leads to higher individual emissions and also to higher global pollution. These effects imply that a policy directed at reducing the cost gap between countries or technological advancements in adaptation technologies lead to higher global emissions under non and full cooperation in the linear damage case.
Having established the benchmark cases, next we turn to the strategic relationships between emissions and adaptation.
4. Strategic relationships between emissions and adaptation
From our optimality conditions above, we characterize two strategic relationships: how a country's emissions respond to its own higher adaptation effort, and how a country's emissions respond to lower emissions by other countries.Footnote 20 This section is devoted to the study of these relationships which are key to understanding the incentives for emissions abatement analyzed in section 5. Our results generalize the two-country case by Ebert and Welsch (Reference Ebert and Welsch2011, Reference Ebert and Welsch2012) to the n-country case with two-group heterogeneity. Our results differ from theirs because we also study the effect of cost heterogeneity on these strategic relationships. In particular, we analyse how reducing the adaptation cost gap between high- and low-cost countries affects a country's incentives to emit, in addition to analysing the existence of carbon leakage.Footnote 21 We start with the strategic relationship between a country's emissions and its adaptation effort.
We obtain the response of a country's emissions to its own higher adaptation effort by totally differentiating the first-order conditions and solving for this relationship. We show in proposition 1 that this strategic relationship depends on the curvature of the damage function and on the cost of adaptation.
Proposition 1.
Emissions and adaptation are strategic complements when damages are linear while they can be either complements or substitutes when damages are non-linear.
Proof: The response of emissions to higher adaptation effort has the same sign for both the non-cooperative and the full cooperative outcome. Let us consider the non-cooperative case first. We substitute E nc = (e i + e −i ) into the first-order conditions (6) and (7) before we totally differentiate these two equations with respect to adaptation. We then solve for:
 $$\displaystyle{{\hbox{d}e_{nc}^j}\over{\hbox{d}a_{nc}^j}}=\displaystyle{{c^j \lpar \eta-1\rpar }\over{\beta E_{nc}}}\lpar a^j - \omega\rpar + \displaystyle{{E_{nc}^{\eta - 1}}\over{\beta}}. $$
$$\displaystyle{{\hbox{d}e_{nc}^j}\over{\hbox{d}a_{nc}^j}}=\displaystyle{{c^j \lpar \eta-1\rpar }\over{\beta E_{nc}}}\lpar a^j - \omega\rpar + \displaystyle{{E_{nc}^{\eta - 1}}\over{\beta}}. $$
Emissions and adaptation effort are complements when
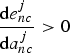 $\displaystyle{{\hbox{d}e_{nc}^{j}}\over{\hbox{d}a_{nc}^{j}}} \gt 0$
and substitutes when
$\displaystyle{{\hbox{d}e_{nc}^{j}}\over{\hbox{d}a_{nc}^{j}}} \gt 0$
and substitutes when
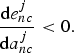 $\displaystyle{{\hbox{d}e_{nc}^{j}}\over {\hbox{d}a_{nc}^{j}}} \lt 0.$
When damages are linear (η = 1), equation (17) reduces to
$\displaystyle{{\hbox{d}e_{nc}^{j}}\over {\hbox{d}a_{nc}^{j}}} \lt 0.$
When damages are linear (η = 1), equation (17) reduces to
![]() $\displaystyle{{1}\over{\beta}} \gt 0 $
for all cost types, which describes a complementarity between emissions and adaptation effort. However, when damages are non-linear (η > 1), the sign of (17) in equilibrium depends on adaptation costs; i.e., emissions and adaptation efforts are strategic complements when c
j
< c̄, where
$\displaystyle{{1}\over{\beta}} \gt 0 $
for all cost types, which describes a complementarity between emissions and adaptation effort. However, when damages are non-linear (η > 1), the sign of (17) in equilibrium depends on adaptation costs; i.e., emissions and adaptation efforts are strategic complements when c
j
< c̄, where
where E
nc
* is the equilibrium level of total emissions.Footnote
22
Alternatively, they are strategic substitutes when c
j
> c̄. Using equations (12) and (13), we find that this strategic relationship also has the same sign in the cooperative case. In this latter case, when damages are linear, the relationship reduces to
 $\displaystyle{{\hbox{d} e_{c}^{j}}\over{\hbox{d} a_{c}^{j}}} = \displaystyle{{n^{j}}\over{\beta}} \gt 0$
, which describes a strategic complementarity between one's private adaptation effort and the emissions of the cooperative group. When damages are non-linear, the coalition's emissions and a country's private adaptation can be complements or substitutes. □
$\displaystyle{{\hbox{d} e_{c}^{j}}\over{\hbox{d} a_{c}^{j}}} = \displaystyle{{n^{j}}\over{\beta}} \gt 0$
, which describes a strategic complementarity between one's private adaptation effort and the emissions of the cooperative group. When damages are non-linear, the coalition's emissions and a country's private adaptation can be complements or substitutes. □
We start our discussion with the linear damage case. Emission and adaptation levels are always strategic complements. This means that a country's private emissions increase as a response to higher adaptation effort in the non-cooperation case. In the cooperative case, this means that, as a country increases its adaptation effort, the emissions a coalition agrees upon also increase. Note also that a perfect complementarity between emissions and adaptation effort implies perfect substitutability between mitigation and adaptation effort.Footnote 23
However, when the damages are non-linear, the response of emissions to higher adaptation effort depends on the parameter values.Footnote
24
We proceed with the well-known quadratic case (η = 2). Using (7) and (17), we obtain the equation that describes the strategic relationship between emissions and adaptation:
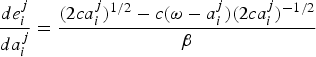 $\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}} = \displaystyle{{\lpar 2ca_{i}^{j}\rpar ^{1/2}-c\lpar {\omega-a}_{i}^{j}\rpar \lpar 2ca_{i}^{j}\rpar ^{-1/2}}\over{\beta}}$
. From this equation, emissions and adaptation effort are strategic substitutes
$\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}} = \displaystyle{{\lpar 2ca_{i}^{j}\rpar ^{1/2}-c\lpar {\omega-a}_{i}^{j}\rpar \lpar 2ca_{i}^{j}\rpar ^{-1/2}}\over{\beta}}$
. From this equation, emissions and adaptation effort are strategic substitutes
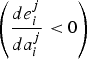 $\left({\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}} \lt 0}\right)$
when ω > 3a
i
j
and complements
$\left({\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}} \lt 0}\right)$
when ω > 3a
i
j
and complements
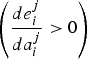 $\left({\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}}\gt 0}\right)$
when ω < 3a
i
j
. We rewrite these conditions in terms of adaptation cost since this strategic relationship is instrumental to understanding the incentives to emit and join a coalition in section 5, as well as to understanding the role of cost heterogeneity in a country's incentives to emit.
$\left({\displaystyle{{de_{i}^{j}}\over{da_{i}^{j}}}\gt 0}\right)$
when ω < 3a
i
j
. We rewrite these conditions in terms of adaptation cost since this strategic relationship is instrumental to understanding the incentives to emit and join a coalition in section 5, as well as to understanding the role of cost heterogeneity in a country's incentives to emit.
Thus, emissions and adaptation effort are strategic substitutes when the cost of adaptation satisfies
![]() $c^{j} \gt {\bar c}=\displaystyle{{3\lpar E_{nc}^{\ast}\rpar ^{2}} \over {2\omega}}$
. For example, this is the case when the cost of adaptation and{/}or the impact of global emissions (ω ) are large. On the contrary, when adaptation cost and/or the impact of global emissions are low, c
j
< c̄, emissions and adaptation effort are complements. In this case, and as seen in equation (7), countries adapt more with low adaptation costs which makes the overall cost of polluting cheaper.Footnote
25
Note also that these relationships hold for all countries, independent of their cost type.
$c^{j} \gt {\bar c}=\displaystyle{{3\lpar E_{nc}^{\ast}\rpar ^{2}} \over {2\omega}}$
. For example, this is the case when the cost of adaptation and{/}or the impact of global emissions (ω ) are large. On the contrary, when adaptation cost and/or the impact of global emissions are low, c
j
< c̄, emissions and adaptation effort are complements. In this case, and as seen in equation (7), countries adapt more with low adaptation costs which makes the overall cost of polluting cheaper.Footnote
25
Note also that these relationships hold for all countries, independent of their cost type.
Now that we have established the relationship between emissions and adaptation effort, we analyze how a change in the cost disparity between countries affects this relationship. We summarize our results in the following.
Result 2.
An exogenous reduction in adaptation costs can change the strategic relationship between emissions and adaptation from substitutability to complementarity.
To see this, we consider three possible scenarios: all countries have effective adaptation technology (c L < c H < c̄), all countries have ineffective adaptation technology (c̄ < c L <c H ), and only some countries have effective adaptation technology (c L < c̄ < c H ). We concentrate on the last scenario which describes a large cost heterogeneity. We analyse again an exogenous change in adaptation costs as we did in section 3. In appendix C, we show that an exogenous reduction in adaptation costs increases c̄. Using this, we can see that, as adaptation costs decrease for high-cost countries (c H ), they can switch from exhibiting strategic substitutability between emission and adaptation levels to having a complementarity relationship. This in turn increases the incentives to adapt and emit more. Finally, note the effect of an exogenous increase in the pure effect of global emissions (ω ). As the impact of global emissions increases, c̄ gets smaller and the likelihood of a complementary relationship between emissions and adaptation effort decreases.
The second strategic relationship we study in this section shows how a country's emissions respond to another country's emission reductions. This is referred to as carbon leakage or emissions being strategic substitutes. In the following, we refer to this relationship as carbon leakage to avoid confusion with the strategic relationship between emissions and adaptation effort discussed above.
Recall that when the possibility to adapt to climate change is ignored, the curvature of the damage function solely determines the existence of carbon leakage (Finus, Reference Finus2003). However, when we account for the possibility to adapt, we show in proposition 2 that the existence of carbon leakage not only depends on the curvature of the damage function, but also on adaptation costs. Technically, adaptation possibilities change the nature of the game by changing the slopes of the best-response functions. This means that cheap adaptation provides a new channel to counter the damages incurred by higher emissions, while expensive adaptation creates barriers to pollution. We summarize the effect of adaptation cost in proposition 2 and the effect of cost heterogeneity in result 3.
Proposition 2.
When damages are linear, there is always carbon leakage in emissions, while when damages are non-linear, the existence of carbon leakage depends on adaptation costs; i.e., for an equilibrium level of total emissions there is no carbon leakage when adaptation costs satisfy
![]() $c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
, while there is carbon leakage otherwise.
$c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
, while there is carbon leakage otherwise.
Proof: We derive the explicit best-response function from equations (6) and (7). We start by substituting (7) into (6), which yields:
 $$e_i^j-\displaystyle{{1}\over{\beta}}\left(\alpha -\omega \lpar e_i^j+e_{-i}\rpar^{\eta -1}+\displaystyle{{\lpar e_i^j+e_{-i}\rpar^{2\eta -1}}\over{c^j \eta }}\right)=0\comma \; $$
$$e_i^j-\displaystyle{{1}\over{\beta}}\left(\alpha -\omega \lpar e_i^j+e_{-i}\rpar^{\eta -1}+\displaystyle{{\lpar e_i^j+e_{-i}\rpar^{2\eta -1}}\over{c^j \eta }}\right)=0\comma \; $$
where e
−i
denotes emissions from all other countries, independently of cost type. We first consider linear damages. We totally differentiate (19) to find
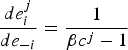 $\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}} = \displaystyle{{1}\over{\beta c^{j} - 1}}$
. The sign determines the existence of leakage; there is carbon leakage when
$\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}} = \displaystyle{{1}\over{\beta c^{j} - 1}}$
. The sign determines the existence of leakage; there is carbon leakage when
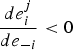 $\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}} \lt 0$
while no carbon leakage when
$\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}} \lt 0$
while no carbon leakage when
 $\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}}\geq 0$
. From the second-order conditions in section 3, β c
j
< 1 always holds and, therefore, carbon leakage always exists when damages are linear. When damages are non-linear, the total differentiation of (19) yields:
$\displaystyle{{d e_{i}^{j}}\over{d e_{-i}}}\geq 0$
. From the second-order conditions in section 3, β c
j
< 1 always holds and, therefore, carbon leakage always exists when damages are linear. When damages are non-linear, the total differentiation of (19) yields:
 $$\displaystyle{{d e_i^j} \over{d e_{-i}}} = \displaystyle{{\lpar 2 \eta - 1\rpar E_{nc}^{2\eta -2} - \lpar \eta - 1 \rpar \eta c^j \omega E_{nc}^{\eta -2}}\over{\beta c^j \eta - \lpar 2 \eta - 1\rpar E_{nc}^{2\eta -2} + \lpar \eta - 1 \rpar \eta c^j \omega E_{nc}^{\eta -2}}}. $$
$$\displaystyle{{d e_i^j} \over{d e_{-i}}} = \displaystyle{{\lpar 2 \eta - 1\rpar E_{nc}^{2\eta -2} - \lpar \eta - 1 \rpar \eta c^j \omega E_{nc}^{\eta -2}}\over{\beta c^j \eta - \lpar 2 \eta - 1\rpar E_{nc}^{2\eta -2} + \lpar \eta - 1 \rpar \eta c^j \omega E_{nc}^{\eta -2}}}. $$
We present the existence of carbon leakage for an equilibrium level of total emissions in terms of adaptation costs. Equation (20) is positive (no carbon leakage) when adaptation costs satisfy
![]() $ c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
where:
$ c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
where:
where E
nc
* denotes the equilibrium level of total emissions. Note also that c̄ in (22) equals c̄ in (18). Thus, for the equilibrium level of total emissions (E
nc
*), carbon leakage exists when
![]() $c^{j} \lt {\underline c}$
or c
j
> c̄.□
$c^{j} \lt {\underline c}$
or c
j
> c̄.□
In both the non-cooperative and cooperative cases with no adaptation possibilities, carbon leakage is never possible when damages are linear (Finus, Reference Finus2003). However, when adaptation is possible, we find that there is always carbon leakage between countries. As other countries emit more, a country responds to higher total pollution by adapting more. As shown before, adaptation and emissions are always complements with linear damages and, therefore, a country responds to others' emissions by emitting more. This implies that the possibility to adapt leads to the existence of carbon leakage with linear damages.
In the non-linear case, however, carbon leakage depends on adaptation costs and we find that its existence is more complex than previously explained in the literature. In addition, cost heterogeneity plays a role in the incentives to emit. For example, if adaptation is highly effective (
![]() $c^{j} \lt {\underline c} $
) or ineffective (
$c^{j} \lt {\underline c} $
) or ineffective (
![]() $c^{j} \gt {\underline c}$
), there is carbon leakage and a country increases emissions as a response to another country's emissions reduction. Let us first consider the case with cheap or effective adaptation. In this case, as others increase their emissions, a country will respond to higher total emissions by adapting more. Since adaptation and emissions are complements with cheap adaptation, countries also respond by increasing their emissions. Next, think of the case with expensive or ineffective adaptation. In this case, this country responds to higher total emissions by reducing adaptation. Since adaptation and emissions are substitutes, a country responds to others by increasing emissions. Finally, when
$c^{j} \gt {\underline c}$
), there is carbon leakage and a country increases emissions as a response to another country's emissions reduction. Let us first consider the case with cheap or effective adaptation. In this case, as others increase their emissions, a country will respond to higher total emissions by adapting more. Since adaptation and emissions are complements with cheap adaptation, countries also respond by increasing their emissions. Next, think of the case with expensive or ineffective adaptation. In this case, this country responds to higher total emissions by reducing adaptation. Since adaptation and emissions are substitutes, a country responds to others by increasing emissions. Finally, when
![]() $c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
, there is no carbon leakage and a country reduces emissions as a response to emissions reduction by others.
$c^{j} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
, there is no carbon leakage and a country reduces emissions as a response to emissions reduction by others.
Proposition 2 also implies that when the gap in adaptation cost is large between countries, some countries exhibit carbon leakage while others do not. We summarize in result 3 the effect of lowering the adaptation cost gap on the existence of carbon leakage.
Result 3.
An exogenous reduction in the adaptation cost gap between countries can change the existence of carbon leakage when damages are quadratic.
In appendix C, we explicitly prove that an exogenous cost reduction leads to an increase in both c and c̄. Not only that, but we show that the increase in c̄ is higher than that of c, which implies that the interval without carbon leakage gets larger. Given this, consider the case of a low adaptation cost country with
![]() $c^{L} \lt {\underline c}$
and a high adaptation cost country with
$c^{L} \lt {\underline c}$
and a high adaptation cost country with
![]() $c^{H} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
. Then, there is carbon leakage in the low adaptation cost countries while there is no carbon leakage in the high adaptation cost countries. An exogenous reduction in adaptation costs leaves low-cost countries' incentives unchanged since c becomes higher. However, for some high adaptation cost countries, this reduction could imply a change in polluting strategy that leads to carbon leakage. Next, let us consider that low adaptation cost countries that satisfy
$c^{H} \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
. Then, there is carbon leakage in the low adaptation cost countries while there is no carbon leakage in the high adaptation cost countries. An exogenous reduction in adaptation costs leaves low-cost countries' incentives unchanged since c becomes higher. However, for some high adaptation cost countries, this reduction could imply a change in polluting strategy that leads to carbon leakage. Next, let us consider that low adaptation cost countries that satisfy
![]() $c^{L}\in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
and high adaptation cost countries satisfy c
H
> c̄. This implies no carbon leakage for low-cost countries and carbon leakage for high-cost countries. In this scenario, a reduction in adaptation costs leads to higher c and c̄, which can shift the existence of carbon leakage.
$c^{L}\in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
and high adaptation cost countries satisfy c
H
> c̄. This implies no carbon leakage for low-cost countries and carbon leakage for high-cost countries. In this scenario, a reduction in adaptation costs leads to higher c and c̄, which can shift the existence of carbon leakage.
Overall, these results imply that heterogeneity in adaptation costs is a key factor that influences the incentives to emit and therefore to join international agreements. We turn to studying these incentives in the next section.
5. Coalition formation and stability
Now that we have established the incentives to emit, we turn to examining the incentives to voluntarily join a coalition and the stability of such self-enforcing agreements. To do so, we analyse a two-stage open membership game. We present the coalition formation game in section 5.1, while 5.2 and 5.3 analyse coalition formation. Section 5.2 presents analytical solutions for the linear damage case while in section 5.3, where we consider non-linear damages, we are unable to derive an analytical solution. In line with Pavlova and De Zeeuw (Reference Pavlova and de Zeeuw2013), numerical examples show that large stable coalitions could potentially exist. However, since such examples are sensitive to changes in parameter values, we discuss instead how the strategic relationships between emissions and adaptation effort and carbon leakage affect the willingness to join a coalition.
5.1. Membership game
We consider a two-stage open-membership Cournot game where countries decide unilaterally whether to ratify the treaty in the first stage. The total number of low and high adaptation cost countries that join the IEA in the first stage is k L and k H respectively, while n − k countries choose to stay out of the coalition, where k = k L + k H . In the following, the subscripts ns and s stand for non-signatory and signatory countries. In the second stage, non-signatory countries choose the individual emissions that maximize their own payoff, while signatory countries decide jointly the emission level that maximizes their aggregate payoff. Thus, non-signatory and signatory countries behave like countries in the non and full cooperation cases in section 3. In this second stage, countries also choose their own private adaptation levels. We solve this game by backward induction starting from the second stage.
In the second stage, non-signatory countries choose emissions and adaptation levels by solving:
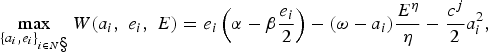 $$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in N\S}}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar =e_{i}\left(\alpha -\beta \displaystyle{{e_{i}}\over{2}}\right)-\lpar \omega -a_{i}\rpar \displaystyle{{E^{\eta }}\over{\eta}}-\displaystyle{{c^{j}}\over{2}}a_{i}^{2}\comma \; $$
$$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in N\S}}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar =e_{i}\left(\alpha -\beta \displaystyle{{e_{i}}\over{2}}\right)-\lpar \omega -a_{i}\rpar \displaystyle{{E^{\eta }}\over{\eta}}-\displaystyle{{c^{j}}\over{2}}a_{i}^{2}\comma \; $$
where N\S is the set of non-signatory countries. This problem is identical to the non-cooperative case in section 3 where the optimality conditions are given by equations (6) and (7). Next, we derive emission and adaptation strategies of signatory countries by solving:
 $$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in S}}\sum_{i\in S}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar =\sum_{i\in S}\left(e_{i}\left(\alpha -\beta \displaystyle{{e_{i}}\over{2}}\right)-\lpar \omega -a_{i}\rpar \displaystyle{{E^{\eta }} \over {\eta}}- \displaystyle{{c^{j}}\over {2}}a_{i}^{2}\right)\comma \; $$
$$\max_{\lcub a_{i}\comma e_{i}\rcub _{i\in S}}\sum_{i\in S}W\lpar a_{i}\comma \; e_{i}\comma \; E\rpar =\sum_{i\in S}\left(e_{i}\left(\alpha -\beta \displaystyle{{e_{i}}\over{2}}\right)-\lpar \omega -a_{i}\rpar \displaystyle{{E^{\eta }} \over {\eta}}- \displaystyle{{c^{j}}\over {2}}a_{i}^{2}\right)\comma \; $$
where S represents the set of signatory countries. The first-order conditions for emissions and adaptation are:
Note that if all countries join the coalition (k = n), the first-order conditions coincide with equations (12) and (13) in the full cooperative case. From these equations, we calculate total emissions generated by non-signatories (E
ns
) and signatories (E
s
). Equation (6), combined with
![]() $E_{ns}=\lpar n^{L}-k^{L}\rpar e_{ns}^{L}+\lpar n^{H}-k^{H}\rpar e_{ns}^{H}$
, yields:
$E_{ns}=\lpar n^{L}-k^{L}\rpar e_{ns}^{L}+\lpar n^{H}-k^{H}\rpar e_{ns}^{H}$
, yields:
 $$E_{ns} = \displaystyle{{1}\over{\beta}}\left[\lpar n-k\rpar \alpha -\left(\! \lpar n-k\rpar \omega -\displaystyle{{n^{L}-k^{L}}\over{\eta c^{L}}}E^{\eta }-\displaystyle{{n^{H}-k^{H}}\over{\eta c^{H}}}E^{\eta }\!\right)E^{\eta -1}\right]. $$
$$E_{ns} = \displaystyle{{1}\over{\beta}}\left[\lpar n-k\rpar \alpha -\left(\! \lpar n-k\rpar \omega -\displaystyle{{n^{L}-k^{L}}\over{\eta c^{L}}}E^{\eta }-\displaystyle{{n^{H}-k^{H}}\over{\eta c^{H}}}E^{\eta }\!\right)E^{\eta -1}\right]. $$
Likewise, equation (25) and
![]() $E_{s}=k^{L}e_{s}^{L}+k^{H}e_{s}^{H}$
yield:
$E_{s}=k^{L}e_{s}^{L}+k^{H}e_{s}^{H}$
yield:
 $$E_{s}=\displaystyle{{1}\over{\beta}}\left[k\alpha -\left(k^{2}\omega -\displaystyle{{kk^{L}}\over{\eta c^{L}}}E^{\eta}-\displaystyle{{kk^{H}}\over{\eta c^{H}}}E^{\eta }\right)E^{\eta -1}\right]. $$
$$E_{s}=\displaystyle{{1}\over{\beta}}\left[k\alpha -\left(k^{2}\omega -\displaystyle{{kk^{L}}\over{\eta c^{L}}}E^{\eta}-\displaystyle{{kk^{H}}\over{\eta c^{H}}}E^{\eta }\right)E^{\eta -1}\right]. $$
Thus, global emissions are the sum of emissions from non-signatories and signatories in (27) and (28), which is the positive root of the equation:
 $$\eqalign{\eta \lpar \beta E-n\alpha \rpar & = E^{\eta -1}\left[-\lpar n-k+k^{2}\rpar \eta \omega +\left(\displaystyle{{n^{L}+k^{L}\lpar k-1\rpar }\over{c^{L}}}\right.\right.\cr & \quad +\left.\left.\displaystyle{{n^{H}+k^{H}\lpar k-1\rpar }\over{c^{H}}} \right)E^{\eta }\right].} $$
$$\eqalign{\eta \lpar \beta E-n\alpha \rpar & = E^{\eta -1}\left[-\lpar n-k+k^{2}\rpar \eta \omega +\left(\displaystyle{{n^{L}+k^{L}\lpar k-1\rpar }\over{c^{L}}}\right.\right.\cr & \quad +\left.\left.\displaystyle{{n^{H}+k^{H}\lpar k-1\rpar }\over{c^{H}}} \right)E^{\eta }\right].} $$
These partial cooperation relationships describe the incentives to emit for a given coalition size. Thus, all countries within the agreement emit equally as in the full cooperative case, while countries outside the coalition behave as singletons. This means that they act in their own self-interest and emit according to their adaptation cost as in the pure non-cooperative case. Furthermore, since global emissions affect all countries equally, these countries' adaptation levels in equilibrium are given by their cost types; every high- (or low-) cost country chooses the same adaptation level independent of whether it signed the agreement. Next, we analyse how the presence of adaptation affects behavior in equilibrium.
Result 4.
The presence of adaptation does not nullify the emissions-abating role of IEAs.
We can see this result by using (6) and (25), along with
![]() $\omega \geq a_{s}^{j}$
and
$\omega \geq a_{s}^{j}$
and
![]() $\omega \geq a_{ns}^{j}$
, which yield
$\omega \geq a_{ns}^{j}$
, which yield
![]() $e_{ns}^{j}-e_{s}^{j}\geq \omega \lpar 2k-1\rpar +a_{ns}^{j} \gt 0.$
Therefore, a non-signatory country always emits more than a signatory country for any coalition size k. Thus, we find adaptation possibilities are not a limiting factor in a climatic coalition. Some argue against putting efforts into adaptation, fearing diminished willingness to abate within environmental agreements (e.g., Faiola and Eilperin, Reference Faiola and Eilperin2009). Contrary to this belief, our result shows that the presence of adaptation does not obstruct the abilities of IEAs to reduce emissions within a coalition.
$e_{ns}^{j}-e_{s}^{j}\geq \omega \lpar 2k-1\rpar +a_{ns}^{j} \gt 0.$
Therefore, a non-signatory country always emits more than a signatory country for any coalition size k. Thus, we find adaptation possibilities are not a limiting factor in a climatic coalition. Some argue against putting efforts into adaptation, fearing diminished willingness to abate within environmental agreements (e.g., Faiola and Eilperin, Reference Faiola and Eilperin2009). Contrary to this belief, our result shows that the presence of adaptation does not obstruct the abilities of IEAs to reduce emissions within a coalition.
Now that we have established the equilibrium behavior of signatories and non-signatories in the second stage, we turn to the first stage and the stability of these coalitions. From the second stage, the equilibrium levels of a
j
, e
i
and E are the solution of (25)–(29) in terms of the stable size k = k
L
+ k
H
. Using these equilibrium results, we write the payoff function in (4) in terms of the coalition size. We follow the stability concept first introduced by d'Aspremont et al. (Reference d'Aspremont, Jacquemin, Gabszewicz and Weymark1983). A coalition is stable when both the internal and external stability conditions hold. Internal stability holds when no country inside the coalition has incentives to leave,
![]() $W_{s}^{j}\lpar k^{j}\comma \; k^{-j}\rpar \geq W_{ns}^{j}\lpar k^{j}-1\comma \; k^{-j}\rpar $
for j = L, H, while external stability holds when no country outside the coalition has incentives to join,
$W_{s}^{j}\lpar k^{j}\comma \; k^{-j}\rpar \geq W_{ns}^{j}\lpar k^{j}-1\comma \; k^{-j}\rpar $
for j = L, H, while external stability holds when no country outside the coalition has incentives to join,
![]() $W_{ns}^{j}\lpar k^{j}\comma \; k^{-j}\rpar \geq W_{s}^{j}\lpar k^{j}+1\comma \; k^{-j}\rpar $
for j = L, H. The stability conditions are computed using the equilibrium welfare levels in the second stage. Following Hoel and Schneider, (Reference Hoel and Schneider1997) and Nkuiya et al., (Reference Nkuiya, Marrouch and Bahel2015), we summarize these conditions using a stability function:
$W_{ns}^{j}\lpar k^{j}\comma \; k^{-j}\rpar \geq W_{s}^{j}\lpar k^{j}+1\comma \; k^{-j}\rpar $
for j = L, H. The stability conditions are computed using the equilibrium welfare levels in the second stage. Following Hoel and Schneider, (Reference Hoel and Schneider1997) and Nkuiya et al., (Reference Nkuiya, Marrouch and Bahel2015), we summarize these conditions using a stability function:
![]() $\phi ^{j}\lpar k^{j}\comma \; k^{-j}\rpar =W_{s}^{j}\lpar k^{j}\comma \; k^{-j}\rpar -W_{ns}^{j}\lpar k^{j}-1\comma \; k^{-j}\rpar \comma \; $
for j = L, H. The coalition
$\phi ^{j}\lpar k^{j}\comma \; k^{-j}\rpar =W_{s}^{j}\lpar k^{j}\comma \; k^{-j}\rpar -W_{ns}^{j}\lpar k^{j}-1\comma \; k^{-j}\rpar \comma \; $
for j = L, H. The coalition
![]() $\lpar k^{L}\comma \; k^{H}\rpar $
is internally stable when
$\lpar k^{L}\comma \; k^{H}\rpar $
is internally stable when
![]() $\phi ^{j}\lpar k^{L}\comma \; k^{H}\rpar \geq 0$
for j = L, H hold, and externally stable when
$\phi ^{j}\lpar k^{L}\comma \; k^{H}\rpar \geq 0$
for j = L, H hold, and externally stable when
![]() $\phi ^{L}\lpar k^{L}+1\comma \; k^{H}\rpar \leq 0$
and
$\phi ^{L}\lpar k^{L}+1\comma \; k^{H}\rpar \leq 0$
and
![]() $\phi ^{H}\lpar k^{L}\comma \; k^{H}+1\rpar \leq 0$
hold. The stable coalition size k = k
L
+ k
H
holds these two conditions simultaneously.
$\phi ^{H}\lpar k^{L}\comma \; k^{H}+1\rpar \leq 0$
hold. The stable coalition size k = k
L
+ k
H
holds these two conditions simultaneously.
Having established the stability conditions, we analyze how adaptation and cost heterogeneity in adaptation change the incentives to join an IEA. We start with the linear damage case.
5.2. Linear damages, η = 1
In the baseline case where adaptation possibilities are ignored, a maximum of three countries join a stable agreement when signatories and non-signatories choose emissions simultaneously (Finus, Reference Finus2003). We first examine the cost symmetry case before turning to cost asymmetry. In both cases, we find that a maximum of three countries form a stable coalition.
Result 5.
The possibilities to adapt do not reduce the incentives to join a coalition when damages are linear, even with heterogeneous adaptation costs.
We prove result 5 analytically in appendix B, where we show that a maximum of three countries join a stable coalition. Since the maximum number of countries that join a coalition is also three in the IEA literature that ignores adaptation possibilities, result 5 implies that adaptation possibilities do not diminish the incentives to join a coalition. Note, however, that when damages are linear, there exists carbon leakage (proposition 1). While carbon leakage often reduces the incentives to join a coalition, in our setting we find that carbon leakage is not a destabilizing factor and that the maximum number of countries that join a coalition is unchanged.
Next, we explore the role of heterogeneity in adaptation costs. Propositions 1 and 2 show that the strategic relationship between emissions and adaptation and the existence of carbon leakage remain unchanged with cost heterogeneity and linear damages. Thus, since the incentives to emit are unchanged, by contradiction, the maximum stable coalition size must be equal to three. Thus, an exogenous reduction in the gap between adaptations costs between countries does not strengthen nor weaken the free-riding incentives. Remember, however, that as shown in section 3, a reduction in cost heterogeneity could increase global emissions. Thus, while we cannot observe changes in participation incentives, policies directed at reducing the adaptation cost gap should consider such an adverse effects on global emissions.
Our result sheds some light on the role of adaptation in changing country incentives to join IEAs. As mentioned before, some argue against putting efforts into adaptation, fearing diminished willingness to join international agreements to reduce emissions. (e.g., Faiola and Eilperin, Reference Faiola and Eilperin2009). Contrary to this belief, our results show that, when damages are linear, the incentives to join an agreement are unchanged. This is so because the complementarity between emissions and adaptation leads to carbon leakages between countries. Thus, the possibility to adapt to climate change creates a new channel to respond to changes in emissions instead of creating barriers for coalition formation.
5.3. Quadratic damages, η = 2
Next, we turn to non-linear damages where we focus on the widely used quadratic damage specification (η = 2). Recall that, when adaptation possibilities are ignored, a maximum of two countries choose to join a stable agreement when signatories and non-signatories choose emissions simultaneously (Finus, Reference Finus2003). Accounting for adaptation possibilities, we identified in section 4 how the incentives to emit depend on each country's adaptation level (equation 17) and on other countries' emission strategies (equation 20). In the following, we discuss how these relationships affect the willingness to join a coalition. Figure 1 presents the incentives to emit for an equilibrium level of total emissions given different adaptation costs with c and c̄ given by equations (21) and (22), respectively.

Figure 1. Strategic relationships between variables in terms of adaptation cost when damages are quadratic
We start with the symmetric case where adaptation costs are identical for all countries. Our results are summarized in result 6.
Result 6.
When damages are quadratic and adaptation costs are homogenous, a large coalition is unlikely with cheap and effective adaptation cost. The willingness to join a coalition may increase adaptation costs.
We first consider the case with effective adaptation (c < c), where there is carbon leakage and emissions and adaptation are complements (figure 1). Carbon leakage enhances free-riding incentives as other countries abate their emissions. Furthermore, the strategic complementarity between emissions and adaptation effort provides a country with incentives to increase individual emissions in response to effective adaptation. As such, these two effects reinforce the incentives to emit and a large coalition size is unlikely to form. This scenario is perhaps the most pessimistic one from the perspective of a global agreement since each country takes care of its own pollution problem.
However, for higher adaptation cost (
![]() $c \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
), there is no carbon leakage although emissions and adaptation are still complements. This complementarity indicates that, as a country adapts more, individual emissions also increase, which weakens the incentives to collaborate on abatement. However, the lack of carbon leakage enhances the incentives to join a coalition. Thus, these two contradictory effects are at play when a country decides to join an agreement. This implies that, when the first effect is smaller than the second one, a country's willingness to join a coalition is enhanced. In reality, specific parameter values determine the magnitude of these effects.
$c \in \lsqb {\underline c}\comma \; {\bar c}\rsqb $
), there is no carbon leakage although emissions and adaptation are still complements. This complementarity indicates that, as a country adapts more, individual emissions also increase, which weakens the incentives to collaborate on abatement. However, the lack of carbon leakage enhances the incentives to join a coalition. Thus, these two contradictory effects are at play when a country decides to join an agreement. This implies that, when the first effect is smaller than the second one, a country's willingness to join a coalition is enhanced. In reality, specific parameter values determine the magnitude of these effects.
Finally, we turn to the case with ineffective adaptation (c > c̄); emissions and adaptation effort are strategic substitutes and carbon leakage exists. This implies that, on the one hand, the strategic substitutability between emissions and adaptation provides a country with incentives to lower individual emissions. On the other hand, carbon leakage leads to free-riding incentives. Again, these two contradictory effects are at play when a country chooses to join a coalition.
Next, we turn to cost asymmetry. When low and high adaptation cost countries are in the same cost range (figure 1), we find the same effects as those described in the symmetric case. Next, we turn to the case with large cost asymmetry where we find two relevant scenarios that we summarize in result 7.
Result 7.
When damages are quadratic and adaptation costs are heterogeneous, the willingness to join a coalition changes as the cost gap narrows. When cost heterogeneity is large, a cost reduction may strengthen participation incentives, while when cost heterogeneity is smaller, such reduction weakens participation incentives.
First, we consider the case where high adaptation cost countries have an ineffective adaptation technology;
![]() $c^{L} \lt{\underline c}$
and
$c^{L} \lt{\underline c}$
and
![]() $c^{H}\gt {\bar c}$
. This, for example, could be the case of developed countries with effective adaptive capacity and the case of emerging economies with a costlier adaptation option. As described above, low-cost countries in this case are unlikely to join a coalition whereas high-cost countries may have incentives to join a coalition. Thus, it seems unlikely that a large stable agreement would arise when half the countries have cheap and effective adaptation costs (
$c^{H}\gt {\bar c}$
. This, for example, could be the case of developed countries with effective adaptive capacity and the case of emerging economies with a costlier adaptation option. As described above, low-cost countries in this case are unlikely to join a coalition whereas high-cost countries may have incentives to join a coalition. Thus, it seems unlikely that a large stable agreement would arise when half the countries have cheap and effective adaptation costs (
![]() $c^{L} \lt {\underline c}$
).Footnote
26
$c^{L} \lt {\underline c}$
).Footnote
26
In this scenario, the cost gap between the developed and developing countries increases further when, for example, low-cost countries develop even more efficient adaptation technologies (lowering c L ). We show in appendix C that such reduction shifts both c and c̄ to the right in figure 1. While the incentives of high-cost countries may change, low-cost countries' incentives to emit are reinforced, which makes them less likely to participate in an agreement. On the other hand, if the cost asymmetry is reduced by, for example, a policy directed at increasing adaptation technology transfers from developed to developing countries, then high-cost countries are able to lower their adaptation costs. This cost reduction also shifts both c and c̄ to the right in figure 1. However, a substantial cost reduction can make adaptation effective for developing countries, thus reversing the relationship between emissions and adaptation from being substitutes to complements. Note also that since such a policy has the potential of eliminating leakages for high-cost countries, it can be used as a device to promote their emissions abatement. This, however, comes at the cost of adaptation reinforcing individual emissions. Therefore, a policy aimed at reducing cost heterogeneity among countries might not improve participation incentives.
Secondly, we consider the case where both types of countries have an effective adaptation technology;
![]() $c^{L} \lt {\underline c}$
and
$c^{L} \lt {\underline c}$
and
![]() ${\underline c} \lt c^{H} \lt {\bar c}$
. High-cost countries may have incentives to form a coalition whereas low-cost countries are unlikely to form a coalition. In this case, a policy directed at reducing the cost gap may potentially eliminate any prospects for a successful agreement. This is so because a policy that reduces costs can shift c to the right such that it creates carbon leakage for high-cost countries. In these case, all countries end up in a scenario without incentives to form a coalition.
${\underline c} \lt c^{H} \lt {\bar c}$
. High-cost countries may have incentives to form a coalition whereas low-cost countries are unlikely to form a coalition. In this case, a policy directed at reducing the cost gap may potentially eliminate any prospects for a successful agreement. This is so because a policy that reduces costs can shift c to the right such that it creates carbon leakage for high-cost countries. In these case, all countries end up in a scenario without incentives to form a coalition.
6. Conclusion and policy implications
In this paper we study the incentives to join IEAs when countries have the option to adapt to climate change, in addition to emissions abatement. We are particularly interested in the impact of cross-country differences in adaptation costs on the incentives to emit. We find that a country's incentives to join a coalition depends on two effects: the strategic relationship between emissions and adaptation, and carbon leakage. Our results suggest that the possibility to adapt to climate change does not necessarily reduce participation incentives. Furthermore, depending on the effectiveness of adaptation, a policy aimed at reducing the adaptation cost gap can either strengthen or weaken participation incentives.
Our results have implications for policies directed at reducing the gap in adaptation costs between developed and developing countries. For example, the Cancún Adaptation Fund,Footnote 27 established in 2010 to reduce the technological gap that exists between developed (low-cost) and developing (high-cost) countries. We find that a policy directed at reducing the cost gap in adaptation may increase global emissions without necessarily improving incentives to form a coalition. Nonetheless, such a policy must consider that the incentive to join a coalition might be altered when heterogeneity decreases or ceases to exist.
Our results also have implications for policies directed at regulating leakages. When adaptation costs are high, a policy aimed at reducing leakages may change the sign of the strategic relationship between emissions and adaptation. In our setting, such a policy could weaken the incentives to join a coalition. Policy makers then ought to be mindful of such a perverse outcome (see, for example, Kallbekken, Reference Kallbekken2007).
Our discussion draws attention to existing international climate policies, such as the Cancún Adaptation Fund or the Clean Development Mechanism, as we show that such policies change the incentives to form large coalitions. Our results indicate that heterogeneity among countries can change participation incentives and, hence, policies directed at reducing these heterogeneities could create barriers and opportunities for coalition formation.
Finally, we summarize some of the limitations of our study and we make suggestions for further research. First, in this study we have assumed that the effect of pollution, (ω), is identical for all countries. While it is likely that global emissions affect each country differently, we chose to abstract from this heterogeneity and concentrate on the role of cross-country differences in adaptation possibilities. An extension could be to account for heterogeneity in both individual damages and adaptation possibilities. Another possible extension is to analyze transfer programs that reduce adaptation costs between developed and developing countries.Footnote 28 Despite these limitations, our paper provides a complementary explanation to better understand the incentives to abate and join IEAs.
Appendix A: Comparison of total emissions in the two polar cases
Linear case, η = 1
From equations (9) and (14), we obtain total emissions for the no and full cooperation given by (15) and (16).
An interior solution where countries generate positive emission levels requires the following two conditionsFootnote 29 :
 $$\beta \gt n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right).$$
$$\beta \gt n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right).$$
From total emissions in the polar cases in equations (15) and (16), we derive:
 $$E_{nc}-E_{c}= n\lpar n-1\rpar \displaystyle{{\beta \omega -\alpha \left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}\over{\left(\beta -\left(\displaystyle{{n^{H}}\over{c^{H}} }+\displaystyle{{n^{L}}\over {c^{L}}}\right)\right)\left(\beta -n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)\right)}}. $$
$$E_{nc}-E_{c}= n\lpar n-1\rpar \displaystyle{{\beta \omega -\alpha \left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}\over{\left(\beta -\left(\displaystyle{{n^{H}}\over{c^{H}} }+\displaystyle{{n^{L}}\over {c^{L}}}\right)\right)\left(\beta -n\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)\right)}}. $$
Assume by contradiction that E nc ≤ E c . In this case, given the existence assumptions A.1 and A.2, equation (A.3) implies that:
 $$\omega\leq \displaystyle{{\alpha}\over{\beta}} \left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}} \over{c^{L}}}\right). $$
$$\omega\leq \displaystyle{{\alpha}\over{\beta}} \left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}} \over{c^{L}}}\right). $$
Rearranging (A.4) leads us to
 $$a_{nc}^L \gt \displaystyle{{1} \over {c^L}} \displaystyle{{n \omega}\over {\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}.$$
$$a_{nc}^L \gt \displaystyle{{1} \over {c^L}} \displaystyle{{n \omega}\over {\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}.$$
Combining this relation with the assumption that no over-adaptation is possible (i.e.,
![]() $a_{nc}^{L} \lt \omega$
), we get
$a_{nc}^{L} \lt \omega$
), we get
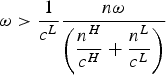 $\omega \gt \displaystyle{{1}\over{c^{L}}} \displaystyle{{n \omega}\over {\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}$
. This implies that E
nc
≤ E
c
holds if and only if c
L
> c
H
. Since this condition is a contradiction with c
H
> c
L
, we necessarily have
$\omega \gt \displaystyle{{1}\over{c^{L}}} \displaystyle{{n \omega}\over {\left(\displaystyle{{n^{H}}\over{c^{H}}}+\displaystyle{{n^{L}}\over{c^{L}}}\right)}}$
. This implies that E
nc
≤ E
c
holds if and only if c
L
> c
H
. Since this condition is a contradiction with c
H
> c
L
, we necessarily have
Non-linear case, η > 1
We define
![]() $l\lpar E\rpar \equiv \eta \lpar \beta E - n\alpha \rpar $
as a function given by the left-hand sides of both equations (9) and (14). We also denote
$l\lpar E\rpar \equiv \eta \lpar \beta E - n\alpha \rpar $
as a function given by the left-hand sides of both equations (9) and (14). We also denote
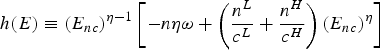 $h\lpar E\rpar \equiv \lpar E_{nc}\rpar ^{\eta-1} \left[-n \eta \omega+\left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E_{nc}\rpar^{\eta}\right]$
as the right-hand side of (9) and
$h\lpar E\rpar \equiv \lpar E_{nc}\rpar ^{\eta-1} \left[-n \eta \omega+\left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E_{nc}\rpar^{\eta}\right]$
as the right-hand side of (9) and
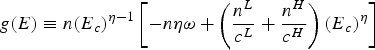 $g\lpar E\rpar \equiv n \lpar E_{c} \rpar ^{\eta-1} \left[-n \eta \omega+ \left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E{_{c}}\rpar^{\eta} \right]$
as the right-hand side of (14). We represent these functions in figure 2, with η > 1, where E
nc
is defined by the intersection between l(E) and h(E), while E
c
is given by the intersection between l(E) and g(E). From the benefit function in (1), total emissions must be smaller than
$g\lpar E\rpar \equiv n \lpar E_{c} \rpar ^{\eta-1} \left[-n \eta \omega+ \left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E{_{c}}\rpar^{\eta} \right]$
as the right-hand side of (14). We represent these functions in figure 2, with η > 1, where E
nc
is defined by the intersection between l(E) and h(E), while E
c
is given by the intersection between l(E) and g(E). From the benefit function in (1), total emissions must be smaller than
![]() $B \equiv n \alpha/\beta$
, which is true for both
$B \equiv n \alpha/\beta$
, which is true for both
![]() $E_{c}^{\ast}$
and
$E_{c}^{\ast}$
and
![]() $E_{nc}^{\ast}$
as illustrated in figure 2. Then, we necessarily have
$E_{nc}^{\ast}$
as illustrated in figure 2. Then, we necessarily have
![]() $E_{c}^{\ast}<E_{nc}^{\ast}$
. For adaptation, since
$E_{c}^{\ast}<E_{nc}^{\ast}$
. For adaptation, since
![]() $E_{nc}^{\ast}>E_{c}^{\ast}$
, by conditions (7) and (12), the result follows.
$E_{nc}^{\ast}>E_{c}^{\ast}$
, by conditions (7) and (12), the result follows.

Figure 2. The comparison between non-cooperative (E nc *) and cooperative (E c *) total emissions
Appendix B: Proof of result 5
As defined in the membership game in section 5.1, the stability function depends on the stable size k. We rewrite the stability condition
![]() $\phi \lpar k\rpar =W_{s}\lpar k\rpar -W_{ns}\lpar k-1\rpar $
as:
$\phi \lpar k\rpar =W_{s}\lpar k\rpar -W_{ns}\lpar k-1\rpar $
as:
where
![]() $\Omega \lpar k\comma \; n\rpar =\lpar 3-k\rpar \lpar c\beta \rpar ^{2}+2\lpar k^{3}-4k^{2}+\lpar n+3\rpar k-n-2\rpar \lpar c\beta \rpar -k^{5}+5k^{4}-\lpar 2n+7\rpar k^{3}+\lpar 4n+3\rpar k^{2}+\lpar 2n-n^{2}\rpar k-n^{2}$
. Ω (k, n) is a second-degree polynomial (in c β) with the following roots:
$\Omega \lpar k\comma \; n\rpar =\lpar 3-k\rpar \lpar c\beta \rpar ^{2}+2\lpar k^{3}-4k^{2}+\lpar n+3\rpar k-n-2\rpar \lpar c\beta \rpar -k^{5}+5k^{4}-\lpar 2n+7\rpar k^{3}+\lpar 4n+3\rpar k^{2}+\lpar 2n-n^{2}\rpar k-n^{2}$
. Ω (k, n) is a second-degree polynomial (in c β) with the following roots:
where
![]() $\Delta=-12k+7n+kn^{2}+4k^{2}n-17kn+16k^{2}-4k^{3}+n^{2}+4.$
$\Delta=-12k+7n+kn^{2}+4k^{2}n-17kn+16k^{2}-4k^{3}+n^{2}+4.$
Any coalition of size k ≥ 4 is internally stable if and only if
![]() $\phi \lpar k\rpar \geq0$
. Since all terms multiplying Ω (k, n) are positive, this condition holds when
$\phi \lpar k\rpar \geq0$
. Since all terms multiplying Ω (k, n) are positive, this condition holds when
![]() $\Omega \lpar k\comma \; n\rpar \geq0$
. This inequality holds if and only if
$\Omega \lpar k\comma \; n\rpar \geq0$
. This inequality holds if and only if
![]() $c\beta\in\lsqb \beta_{2s}\comma \; \beta_{1s}\rsqb $
. In addition, we find that
$c\beta\in\lsqb \beta_{2s}\comma \; \beta_{1s}\rsqb $
. In addition, we find that
![]() $\beta_{2s}<\beta_{1s}<n^{2}$
. These results combined with the existence assumption (A.2) suggest that any coalition of size k ≥ 4 cannot be internally stable.
$\beta_{2s}<\beta_{1s}<n^{2}$
. These results combined with the existence assumption (A.2) suggest that any coalition of size k ≥ 4 cannot be internally stable.
It remains to show that a coalition of size k = 3 may be stable. By setting k = 3, we get
![]() $\Omega \lpar 3\comma \; n\rpar =4c\beta\lpar n-1\rpar -\lpar 3n^{2}+13n\rpar $
. Since Ω (3, n) is positive when
$\Omega \lpar 3\comma \; n\rpar =4c\beta\lpar n-1\rpar -\lpar 3n^{2}+13n\rpar $
. Since Ω (3, n) is positive when
![]() $c\beta\geq \lpar 3n^{2}+13n\rpar /4\lpar n-1\rpar $
, we find that the maximum number of countries that can join a coalition is equal to three when this condition holds.
$c\beta\geq \lpar 3n^{2}+13n\rpar /4\lpar n-1\rpar $
, we find that the maximum number of countries that can join a coalition is equal to three when this condition holds.
Appendix C: The effect of changes in adaptation cost on c and c̄
In this section we show that an exogenous reduction of adaptation cost increases both c and
![]() ${\bar c}$
with quadratic damages (η = 2). We develop this proof in two steps. We first show how changes in adaptation cost affect total emissions and, next, we show how total emissions affect the range of adaptation cost [c, c̄]. We formulate this proof for the non-cooperative case but it is easy to see that it also applies to the cooperative case. In this proof, we denote E equal to E
nc
.
${\bar c}$
with quadratic damages (η = 2). We develop this proof in two steps. We first show how changes in adaptation cost affect total emissions and, next, we show how total emissions affect the range of adaptation cost [c, c̄]. We formulate this proof for the non-cooperative case but it is easy to see that it also applies to the cooperative case. In this proof, we denote E equal to E
nc
.
To see how changes in adaptation cost affect emissions, we turn to figure 3 which shows the equilibrium level of total emissions for the quadratic case in equation (9). We define the left-hand side and the right-hand side of (9) as
![]() $l\lpar E\rpar \equiv \eta \lpar \beta E - n\alpha \rpar $
and
$l\lpar E\rpar \equiv \eta \lpar \beta E - n\alpha \rpar $
and
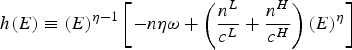 $h\lpar E\rpar \equiv \lpar E\rpar ^{\eta-1}\left[-n \eta \omega + \left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E \rpar^{\eta}\right]$
, respectively. In figure 3, the intersection between the two curves illustrates total emissions in the quadratic case. Next, by taking the first-order derivatives of l(E) and h(E) with respect to adaptation cost, we can see that changes in adaptation costs leave l(E) unchanged
$h\lpar E\rpar \equiv \lpar E\rpar ^{\eta-1}\left[-n \eta \omega + \left(\displaystyle{{n^{L}}\over{c^{L}}}+\displaystyle{{n^{H}}\over{c^{H}}}\right)\lpar E \rpar^{\eta}\right]$
, respectively. In figure 3, the intersection between the two curves illustrates total emissions in the quadratic case. Next, by taking the first-order derivatives of l(E) and h(E) with respect to adaptation cost, we can see that changes in adaptation costs leave l(E) unchanged
![]() $\left(\displaystyle{{\partial l\lpar E\rpar }\over{\partial c}} = 0 \right)$
while h(E) becomes smaller
$\left(\displaystyle{{\partial l\lpar E\rpar }\over{\partial c}} = 0 \right)$
while h(E) becomes smaller
![]() $\left(\displaystyle{{\partial h\lpar E\rpar }\over{\partial c}} \lt 0 \right)$
. This implies that an exogenous cost reduction in adaptation costs will shift h(E) upwards, which yields higher total emissions at the intersection between l(E) and h′(E). This new intersection in figure 3 illustrates that an exogenous reduction in adaption costs leads to an increase in total emissions ((E*)′).
$\left(\displaystyle{{\partial h\lpar E\rpar }\over{\partial c}} \lt 0 \right)$
. This implies that an exogenous cost reduction in adaptation costs will shift h(E) upwards, which yields higher total emissions at the intersection between l(E) and h′(E). This new intersection in figure 3 illustrates that an exogenous reduction in adaption costs leads to an increase in total emissions ((E*)′).

Figure 3. The effect of changes in adaptation cost on total emissions in the quadratic case
Next, we analyze the effect of higher total emissions in equilibrium on the range of adaptation cost
![]() $\lsqb \underline{c}\comma \; \bar{c}\rsqb $
in equations (21) and (22):
$\lsqb \underline{c}\comma \; \bar{c}\rsqb $
in equations (21) and (22):
Thus, higher equilibrium levels of total emissions leads to an increase in the interval [c, c̄]. Note that (C.2) is larger than (C.1), which implies that the [c, c̄] interval becomes larger in response to an exogenous reduction in adaptation costs. While our main results hold, this finding is interesting on its own as it shows that, as we develop cheaper adaptation technologies, the interval with no leakage becomes larger.
Therefore, we can conclude that an exogenous reduction in adaptation costs leads to higher total emissions in equilibrium, which in turn increases both c and c̄.





