Article contents
SPECIFICATION TESTS FOR LATTICE PROCESSES
Published online by Cambridge University Press: 19 August 2014
Abstract
We consider an omnibus test for the correct specification of the dynamics of a sequence 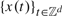 $\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ in a lattice. As it happens with causal models and d = 1, its asymptotic distribution is not pivotal and depends on the estimator of the unknown parameters of the model under the null hypothesis. One first main goal of the paper is to provide a transformation to obtain an asymptotic distribution that is free of nuisance parameters. Secondly, we propose a bootstrap analog of the transformation and show its validity. Thirdly, we discuss the results when
$\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ in a lattice. As it happens with causal models and d = 1, its asymptotic distribution is not pivotal and depends on the estimator of the unknown parameters of the model under the null hypothesis. One first main goal of the paper is to provide a transformation to obtain an asymptotic distribution that is free of nuisance parameters. Secondly, we propose a bootstrap analog of the transformation and show its validity. Thirdly, we discuss the results when 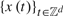 $\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ are the errors of a parametric regression model. As a by product, we also discuss the asymptotic normality of the least squares estimator of the parameters of the regression model under very mild conditions. Finally, we present a small Monte Carlo experiment to shed some light on the finite sample behavior of our test.
$\left\{ {x\left( t \right)} \right\}_{t \in Z^d } $ are the errors of a parametric regression model. As a by product, we also discuss the asymptotic normality of the least squares estimator of the parameters of the regression model under very mild conditions. Finally, we present a small Monte Carlo experiment to shed some light on the finite sample behavior of our test.
- Type
- ARTICLES
- Information
- Econometric Theory , Volume 31 , Issue 2: Haavelmo Memorial Issue: Part Two , April 2015 , pp. 294 - 336
- Copyright
- Copyright © Cambridge University Press 2014
References
REFERENCES
- 2
- Cited by


