Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-12T04:06:14.083Z Has data issue: false hasContentIssue false
  • English
  • Français

IDENTIFYING THE BROWNIAN COVARIATION FROM THE CO-JUMPS GIVEN DISCRETE OBSERVATIONS

Published online by Cambridge University Press:  19 January 2012

Cecilia Mancini  and
Fabio Gobbi
Cecilia Mancini*
Affiliation:
University of Florence
Fabio Gobbi
Affiliation:
University of Bologna
*
*Address correspondence to Cecilia Mancini, Dipartimento di Matematica per le Decisioni, Università di Firenze, via delle Pandette 9, 50127 Firenze; e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

When the covariance between the risk factors of asset prices is due to both Brownian and jump components, the realized covariation (RC) approaches the sum of the integrated covariation (IC) with the sum of the co-jumps, as the observation frequency increases to infinity, in a finite and fixed time horizon. In this paper the two components are consistently separately estimated within a semimartingale framework with possibly infinite activity jumps. 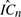The threshold (or truncated) estimator is used, which substantially excludes from RC all terms containing jumps. Unlike in Jacod (2007, Universite de Paris-6) and Jacod (2008, Stochastic Processes and Their Applications 118, 517–559), no assumptions on the volatilities’ dynamics are required. In the presence of only finite activity jumps: 1) central limit theorems (CLTs) for 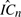and for further measures of dependence between the two Brownian parts are obtained; the estimation error asymptotic variance is shown to be smaller than for the alternative estimators of IC in the literature; 2) by also selecting the observations as in Hayashi and Yoshida (2005, Bernoulli 11, 359–379), robustness to nonsynchronous data is obtained. The proposed estimators are shown to have good finite sample performances in Monte Carlo simulations even with an observation frequency low enough to make microstructure noises’ impact on data negligible.

Type
ARTICLES
Information
Econometric Theory , Volume 28 , Issue 2 , April 2012 , pp. 249 - 273
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aït-Sahalia, Y. & Jacod, J. (2009a) Estimating the degree of activity of jumps in high frequency data. Annals of Statistics 37, 2202–2244.CrossRefGoogle Scholar
Aït-Sahalia, Y. & Jacod, J. (2009b) Testing for jumps in a discretely observed process. Annals of Statistics 37, 184–222.CrossRefGoogle Scholar
Barndorff-Nielsen, O.E., Gravensen, S., Jacod, J., Podolskij, M., & Shephard, N. (2006) A central limit theorem for realised power and bipower variation of continuous semimartingales. In Kabanov, Y., Liptser, R., & Stojanov, J. (eds.), From Stochastic Calculus to Mathematical Finance, Festschrift for Albert Shiryaev. Springer-Verlag.Google Scholar
Barndorff-Nielsen, O.E. & Shephard, N. (2004a) Econometric analysis of realized covariation: High frequency based covariance, regression and correlation in financial economics. Econometrica 72, 885–925.CrossRefGoogle Scholar
Barndorff-Nielsen, O.E. & Shephard, N. (2004b) Measuring the Impact of Jumps in Multivariate Price Processes Using Bipower Covariation. Working paper, Oxford University.Google Scholar
Barndorff-Nielsen, O.E. & Shephard, N. (2007) Variation, jumps and high frequency data in financial econometrics. In Blundell, R., Persson, T., & Newey, W.K. (eds.), Advances in Economics and Econometrics. Theory and Applications, Ninth World Congress, pp. 328–372. Cambridge University Press.CrossRefGoogle Scholar
Bjork, T., Kabanov, Y., & Runggaldier, W. (1997) Bond market structure in the presence of marked point processes. Mathematical Finance 7(2), 211–223.CrossRefGoogle Scholar
Bollerslev, T., Law, T., & Tauchen, G. (2008) Risk, jumps and diversification. Journal of Econometrics 144(1), 234–256.CrossRefGoogle Scholar
Boudt, K., Croux, C., & Laurent, S. (in press) Outlyingness weighted quadratic covariation. Journal of Financial Econometrics, forthcoming.Google Scholar
Carr, P., Geman, H., Madan, D., & Yor, M. (2002) The fine structure of asset returns: An empirical investigation. Journal of Business 75(2), 305–332.CrossRefGoogle Scholar
Cont, R. & Kan, Y.H. (2009) Dynamic Hedging of Portfolio Credit Derivatives. Working paper, available onwww.ssrn.com.CrossRefGoogle Scholar
Cont, R. & Mancini, C. (2011) Nonparametric tests for pathwise properties of semimartingales. Bernoulli 17, 781–813.CrossRefGoogle Scholar
Cont, R. & Tankov, P. (2004) Financial Modelling with jump processes. Chapman and Hall-CRC.Google Scholar
Corsi, F., Pirino, D., & Renò, R. (2010) Threshold bipower variation and the impact of jumps on volatility forecasting. Journal of Econometrics 159, 276–288.CrossRefGoogle Scholar
Das, S. & Uppal, R. (2004) Systemic risk and international portfolio choice. Journal of Finance 59(6), 2809–2834.CrossRefGoogle Scholar
Hayashi, T. & Kusuoka, S. (2008) Consistent estimation of covariation under nonsynchronicity. Statistical Inference for Stochastic Processes 11, 93–106.CrossRefGoogle Scholar
Hayashi, T. & Yoshida, N. (2005) On covariance estimation of non-synchronously observed diffusion processes. Bernoulli 11(2), 359–379.CrossRefGoogle Scholar
Huang, X. & Tauchen, G. (2005) The relative contribution of jumps to total price variance. Journal of Financial Econometrics 3(4), 456–499.CrossRefGoogle Scholar
Jacod, J. (2007) Statistics and High-Frequency Data. SEMSTAT seminar, Technical report, Universite. de Paris-6.Google Scholar
Jacod, J. (2008) Asymptotic properties of realized power variations and related functionals of semimartingales. Stochastic Processes and Their Applications 118, 517–559.CrossRefGoogle Scholar
Jacod, J. & Protter, P. (1998) Asymptotic error distributions for the Euler method for stochastic differential equations. Annals of Probability 26, 267–307.CrossRefGoogle Scholar
Jacod, J. & Shiryaev, A.N. (2003) Limit Theorems for Stochastic Processes, 2nd ed.Springer-Verlag.CrossRefGoogle Scholar
Jacod, J. & Todorov, V. (2009) Testing for common arrivals of jumps for discretely observed multidimensional processes. Annals of Statistics 37(4), 1792–1838.CrossRefGoogle Scholar
Longin, F. & Solnik, B. (2001) Extreme correlation of international equity markets. Journal of Finance 56(2), 649–676.CrossRefGoogle Scholar
Mancini, C. (2001) Disentangling the jumps of the diffusion in a geometric jumping Brownian motion, Giornale dell’Istituto Italiano degli Attuari 64, 19–47.Google Scholar
Mancini, C. (2009) Non-parametric threshold estimation for models with stochastic diffusion coefficient and jumps. Scandinavian Journal of Statistics 36, 270–296.CrossRefGoogle Scholar
Mancini, C. (2010) Central Limit Theorem for Integrated Covariation Estimate in Bidimensional Asset Prices with Stochastic Volatility and Infinite Activity Lévy Jumps. Working paper, University of Florence.Google Scholar
Renò, R. (2003) A closer look at the Epps effect. International Journal of Theoretical and Applied Finance 6, 87–102.CrossRefGoogle Scholar
Revuz, D. & Yor, M. (2001) Continuous Martingales and Brownian Motion. Springer-Verlag.Google Scholar
Todorov, V. & Bollerslev, T. (2010) Jumps and betas: A new framework for disentangling and estimating systematic risks. Journal of Econometrics 157, 220–235.CrossRefGoogle Scholar
Vetter, M. (2010) Limit theorems for bipower variation of semimartingales. Stochastic Processes and Their Applications 120(1), 22–38.CrossRefGoogle Scholar
Woerner, J. (2006) Power and multipower variation: Inference for high frequency data. In Shiryaev, A.N., do Rosário Grossinho, M., Oliviera, P., & Esquivel, M. (eds.), Stochastic Finance, pp. 343–364. Springer-Verlag.CrossRefGoogle Scholar