Hostname: page-component-6bf8c574d5-xtvcr Total loading time: 0 Render date: 2025-02-23T02:04:17.292Z Has data issue: false hasContentIssue false
  • English
  • Français

A NONPARAMETRIC TEST FOR INSTANTANEOUS CAUSALITY WITH TIME-VARYING VARIANCES

Published online by Cambridge University Press:  21 February 2025

Jilin Wu ,
Ruike Wu  and
Zhijie Xiao
Jilin Wu*
Affiliation:
Xiamen University
Ruike Wu
Affiliation:
Shanghai University of Finance and Economics
Zhijie Xiao
Affiliation:
Boston College
*
Address correspondence to Jilin Wu, Department of Finance, School of Economics, Gregory and Paula Chow Institute for studies in Economics, and MOE Key Laboratory of Econometrics, Xiamen University, Xiamen, China, e-mail: [email protected].
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper proposes a consistent nonparametric test with good sampling properties to detect instantaneous causality between vector autoregressive (VAR) variables with time-varying variances. The new test takes the form of the U-statistic, and has a limiting standard normal distribution under the null. We further show that the test is consistent against any fixed alternatives, and has nontrivial asymptotic power against a class of local alternatives with a rate slower than 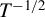$T^{-1/2}$. We also propose a wild bootstrap procedure to better approximate the finite sample null distribution of the test statistic. Monte Carlo experiments are conducted to highlight the merits of the proposed test relative to other popular tests in finite samples. Finally, we apply the new test to investigate the instantaneous causality relationship between money supply and inflation rates in the USA.

Type
ARTICLES
Information
Econometric Theory , First View , pp. 1 - 29
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Jilin Wu acknowledges the supports from the National Natural Science Foundation of China (Grant No. 72371213) and from the NSFC Basic Science Center Project for Econometric Modeling and Economic Policy Studies (Grant No. 71988101). We are most grateful to the Editor, Peter Phillips, for carefully going through an earlier version of the paper and providing many pertinent comments and constructive suggestions that markedly improved the paper. We also would like to thank the Co-Editor (Xu Cheng), and three referees for their constructive comments and suggestions. The authors contributed equally to this paper and are credited in alphabetical order.

References

REFERENCES

Andreou, E., & Ghysels, E. (2002). Detecting multiple breaks in financial market volatility dynamics. Journal of Applied Econometrics , 17, 579–600.CrossRefGoogle Scholar
Bai, J., & Perron, P. (1998). Estimating and testing linear models with multiple structural changes. Econometrica , 66, 47–78.CrossRefGoogle Scholar
Benderly, J., & Zwick, B. (1985). Inflation, real balances, output, and real stock returns. American Economic Review , 75, 1115–1123.Google Scholar
Boubacar, M. Y. (2012). Selection of weak VARMA models by Akaike’s information criteria. Journal of Time Series Analysis , 33, 121–130.CrossRefGoogle Scholar
Breitung, J., & Swanson, N. R. (2002). Temporal aggregation and spurious instantaneous causality in multiple time series models. Journal of Time Series Analysis , 23, 651–665.CrossRefGoogle Scholar
Brown, B. M. (1971). Martingale central limit theorems. Annals of Mathematical Statistics , 42, 59–66.CrossRefGoogle Scholar
Cavanaugh, J. E. (1997). Unifying the derivations for the Akaike and corrected Akaike information criteria. Statistical and Probability Letters , 33, 201–208.CrossRefGoogle Scholar
Cai, Z. W., Wang, Y. F., & Wang, Y. G. (2015). Testing instability in a predictive regression model with nonstationary regressors. Econometric Theory , 31, 953–980.CrossRefGoogle Scholar
Cavaliere, G. (2005). Unit root tests under time-varying variances. Econometric Reviews , 23, 259–292.CrossRefGoogle Scholar
Chen, B., & Hong, Y. (2012). Testing for smooth structural changes in time series models via nonparametric regression. Econometrica , 80, 1157–1183.Google Scholar
Chitturi, R. V. (1974). Distribution of residual autocorrelations in multiple autoregressive schemes. Journal of the American Statistical Association , 69, 928–934.CrossRefGoogle Scholar
Clark, T. (2011). Real-time density forecasts from BVARs with stochastic volatility. Journal of Business and Economic Statistics , 29, 327–341.CrossRefGoogle Scholar
Dufour, J. M., & Taamouti, A. (2010). Short and long run causality measures: Theory and inference. Journal of Econometrics , 154, 42–58.CrossRefGoogle Scholar
Faes, L., & Nollo, G. (2010). Extended causal modelling to assess partial directed coherence in multiple time series with significant instantaneous interactions. Biological Cybernetics , 103, 387–400.CrossRefGoogle ScholarPubMed
Faes, L., Erla, S., Porta, A., & Nollo, G. (2013). A framework for assessing frequency domain causality in physiological time series with instantaneous effects. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences , 371(1997), 20110618.CrossRefGoogle ScholarPubMed
Fu, Z. H., Hong, Y. M., & Wang, X. (2023). On multiple structural breaks in distribution: An empirical characteristic function approach. Econometric Theory , 39, 534–581.CrossRefGoogle Scholar
Gao, J. T., Peng, B., & Yan, Y. Y. (2024). Estimation, inference, and empirical analysis for time-varying VAR models. Journal of Business and Economic Statistics . 42, 310–321 CrossRefGoogle Scholar
Geweke, J. (1982). Measurement of linear dependence and feedback between multiple time series. Journal of the American Statistical Association , 77, 304–313.CrossRefGoogle Scholar
Geweke, J. (1984). Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association , 79, 907–915.CrossRefGoogle Scholar
Gianetto, Q. G., & Raïssi, H. (2015). Testing instantaneous causality in presence of nonconstant unconditional covariance. Journal of Business and Economic Statistics , 33, 46–53.CrossRefGoogle Scholar
Granger, C. W. J. (1969). Investigating causal relations by econometric models and cross-spectral methods. Econometrica , 37, 424–438.CrossRefGoogle Scholar
Granger, C. W. J. (1988). Some recent developments in a concept of causality. Journal of Econometrics , 39, 199–211.CrossRefGoogle Scholar
Granger, C. W. J., & Hyung, N. (2004). Occasional structural breaks and long memory with an application to the SP 500 absolute stock returns. Journal of Empirical Finance , 11, 399–421.CrossRefGoogle Scholar
Groen, J., Paap, R., & Ravazzolo, F. (2013). Real-time inflation forecasting in a changing world. Journal of Business and Economic Statistics , 31, 29–44.CrossRefGoogle Scholar
Hafner, C. (2009). Causality and forecasting in temporally aggregated multivariate GARCH processes. The Econometrics Journal , 12, 127–146.CrossRefGoogle Scholar
Hafner, C., & Linton, O. (2010). Efficient estimation of a multivariate multiplicative volatility model. Journal of Econometrics , 159, 55–73.CrossRefGoogle Scholar
Hammoudeh, S., & Li, H. (2008). sSudden changes in volatility in emerging markets: The case of Gulf Arab stock markets. International Review of Financial Analysis , 17, 47–63.CrossRefGoogle Scholar
Hamori, S., & Tokihisa, A. (1997). Testing for a unit root in the presence of a variance shift. Economics Letters , 57, 245–253.CrossRefGoogle Scholar
Hannan, E. J., & Quinn, B. G. (1979). The determination of the order of an autoregression. Journal of the Royal Statistical Society, Series B , 41, 190–195.CrossRefGoogle Scholar
Hansen, B. E. (1995). Regression with nonstationary volatility. Econometrica , 63, 1113–1132.CrossRefGoogle Scholar
Hansen, B. E. (2001). The new econometrics of structural change: Dating breaks in US labor productivity. Journal of Economic Perspectives 15, 117–128.CrossRefGoogle Scholar
Härdle, W., Mammen, E. (1993). Comparing nonparametric versus parametric regression fits efficiency. The Annals of Statistics , 41, 1926–1947.Google Scholar
Hyvärinen, A., Zhang, K., Shimizu, S., & Hoyer, P. O. (2010). Estimation of a structural vector autoregression model using non-Gaussianity. Journal of Machine Learning Research , 11, 1709–1731.Google Scholar
Hosking, J. R. M. (1980). The multivariate portmanteau statistic. Journal of the American Statistical Association 75, 343–386.CrossRefGoogle Scholar
Hsiao, Z., & Li, Q. (2001). A consistent test for conditional heteroskedasticity in time series regression models. Econometric Theory , 17, 188–221.CrossRefGoogle Scholar
Hu, M., & Liang, H. (2014). A Copula approach to assessing Granger causality. NeuroImage , 100, 125–134.CrossRefGoogle ScholarPubMed
Imhof, J. P. (1961). Computing the distribution of quadratic forms in normal variables. Biometrika , 48, 419–426.CrossRefGoogle Scholar
Juhl, T., & Xiao, Z. J. (2005). A nonparametric test for changing trends. Journal of Econometrics , 127, 179–199.CrossRefGoogle Scholar
Justiniano, A., & Primiceri, G. E. (2008). The time-varying volatility of macroeconomic fluctuations. American Economic Review , 98, 604–641.CrossRefGoogle Scholar
Kim, C. J., & Nelson, C. R. (1999). Has the US economy become more stable? A Bayesian approach based on a Markov-switching model of the business cycle. The Review of Economics and Statistics , 81, 608–616.CrossRefGoogle Scholar
Kim, T., Leybourne, H. S., & Newbold, P. (2002). Unit root tests with a break in innovation variance. Journal of Econometrics , 109, 365–387.CrossRefGoogle Scholar
Lamoureux, C. G., & Lastrapes, W. D. (1990). Persistence in variance, structural change, and the GARCH model. Journal of Business and Economic Statistics , 8, 225–234.CrossRefGoogle Scholar
Lee, T. H., & Ullah, A. (2007). Nonparametric bootstrap tests for neglected nonlinearity in time series regression models. Journal of Nonparametric Statistics , 13, 425–451.CrossRefGoogle Scholar
Li, D., & Li, Q. (2010). Nonparametric semiparametric estimation and testing of econometric models with data dependent smoothing parameters. Journal of Econometrics , 157, 179–190.CrossRefGoogle Scholar
Li, Q., & Racine, J. (2004). Cross validated local linear nonparametric regression. Statistica Sinica , 14, 485–512.Google Scholar
Li, Y., Wei, H. L., Billings, S. A., & Liao, X. F. (2012). Time-varying linear and nonlinear parametric model for Granger causality analysis. Physical Review E , 85, 41906.CrossRefGoogle ScholarPubMed
Li, Q., & Wang, S. (1998). A simple consistent bootstrap test for a parametric regression function. Journal of Econometrics , 87, 145–165.CrossRefGoogle Scholar
Linton, O., & Xiao, Z. J. (2019). Efficient estimation of nonparametric regression in the presence of dynamic heteroskedasticity. Journal of Econometrics , 213, 608–631.CrossRefGoogle Scholar
Liu, C., & Maheu, J. M. (2008). Are there structural breaks in realized volatility?. Journal of Financial Econometrics , 6, 326–360.CrossRefGoogle Scholar
Lütkepohl, H. (2005). New introduction to multiple time series analysis . Springer.CrossRefGoogle Scholar
Mikosch, T., & St $\check{\rm a}$ ric $\check{\rm a}$ , C. (2004). Nonstationarities in financial time series, the long-range dependence, and the IGARCH effects. The Review of Economics and Statistics , 86, 378–390.CrossRefGoogle Scholar
Patilea, V., & Raïssi, H. (2012). Adaptive estimation of vector autoregressive models with time-varying variance: Application to testing linear causality in mean. Journal of Statistical Planning and Inference , 142, 2891–2912.CrossRefGoogle Scholar
Patilea, V., & Raïssi, H. (2013). Corrected Portmanteau tests for VAR models with time varying variance. Journal of Multivariate Analysis , 116, 190–207.CrossRefGoogle Scholar
Pierce, D. A., & Haugh, L. D. (1977). Causality in temporal systems: Characterizations and a survey. Journal of Econometrics , 5, 265–293.CrossRefGoogle Scholar
Raïssi, H. (2011). Testing instantaneous linear Granger causality in presence of nonlinear dynamics. Comptes Rendus Mathematique , 349, 1203–1206.CrossRefGoogle Scholar
Robinson, P. M. (1989). Nonparametric estimation of time-varying parameters. In Hackl, P. (Ed.), Statistical analysis and forecasting of economic structural change (pp. 253–264). Springer.CrossRefGoogle Scholar
Sensier, M., & Van Dijk, D. (2004). Testing for volatility changes in U.S. macroeconomic time series. The Review of Economics and Statistics , 86, 833–839.CrossRefGoogle Scholar
Sims, C. (1972). Money, income, and causality. American Economic Review , 62, 540–552.Google Scholar
Song, X., & Taamouti, A. (2018). Measuring nonlinear Granger causality in mean. Journal of Business and Economics Statistics , 36, 321–333.CrossRefGoogle Scholar
Song, X., & Taamouti, A. (2021). Measuring Granger causality in quantiles. Journal of Business and Economic Statistics , 39, 937–952.CrossRefGoogle Scholar
Taamouti, A., Bouezmarni, T., & El Ghouch, A. (2014). Nonparametric estimation and inference for Granger causality measures. Journal of Econometrics , 180, 251–264.CrossRefGoogle Scholar
Turnovsky, S. J., & Wohar, M. E. (1984). Monetarism and the aggregate economy: Some longer-run evidence. The Review of Economics and Statistics , 66, 619–629.CrossRefGoogle Scholar
Van Dijk, D., Osborn, D. R, & Sensier, M. (2005). Testing for causality in variance in the presence of breaks. Economics Letters , 89, 193–199.CrossRefGoogle Scholar
Vilasuso, J. (2001). Causality tests and conditional heteroskedasticity: Monte Carlo evidence. Journal of Econometrics , 101, 25–35.CrossRefGoogle Scholar
Wu, J. L., Wu, R. K. & Xiao, Z. J. (2022). A nonparametric test for instantaneous causality with time-varying variances. Working paper.Google Scholar
Wu, J. L., Xiao, Z. J. (2018a). A powerful test for changing trends in time series models. Journal of Time Series Analysis , 39, 488–501.CrossRefGoogle Scholar
Wu, J. L., & Xiao, Z. J. (2018b). Testing for changing volatility. The Econometrics Journal , 21, 192–217.CrossRefGoogle Scholar
Xia, Y., & Li, W. K. (2002). Asymptotic behavior of bandwidth selected by cross validation method for local polynomial fitting. Journal of Multivariate Analysis , 83, 265–287.CrossRefGoogle Scholar
Xu, K. L., & Phillips, P. C. B. (2008). Adaptive estimation of autoregressive models with time-varying variances. Journal of Econometrics , 142, 265–280.CrossRefGoogle Scholar
Xu, K. L. (2012). Robustifying multivariate trend tests to nonstationary volatility. Journal of Econometrics , 169, 147–154.CrossRefGoogle Scholar
Zheng, J. X. (1996). A consistent test of functional form via nonparametric estimation techniques. Journal of Econometrics , 75, 263–290.CrossRefGoogle Scholar
Supplementary material: File

Wu et al. supplementary material

Wu et al. supplementary material
Download Wu et al. supplementary material(File)
File 389.8 KB