Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Smith, Murray D.
1988.
CONVERGENT SERIES EXPRESSIONS FOR INVERSE MOMENTS OF QUADRATIC FORMS IN NORMAL VARIABLES.
Australian Journal of Statistics,
Vol. 30,
Issue. 2,
p.
235.
Hayakawa, T.
1989.
Invariant Polynomials and Related Tests.
American Journal of Mathematical and Management Sciences,
Vol. 9,
Issue. 1-2,
p.
69.
Smith, Murray D.
1989.
On the expectation of a ratio of quadratic forms in normal variables.
Journal of Multivariate Analysis,
Vol. 31,
Issue. 2,
p.
244.
Smith, Murray D.
1993.
EXPECTATIONS OF RATIOS OF QUADRATIC FORMS IN NORMAL VARIABLES: EVALUATING SOME TOP‐ORDER INVARIANT POLYNOMIALS.
Australian Journal of Statistics,
Vol. 35,
Issue. 3,
p.
271.
Skeels, Christopher L.
1995.
Some Exact Results for Estimators of the Coefficients on the Exogenous Variables in a Single Equation.
Econometric Theory,
Vol. 11,
Issue. 3,
p.
484.
Li, Runze
1997.
The expected values of invariant polynomials with matrix argument of elliptical distributions.
Acta Mathematicae Applicatae Sinica,
Vol. 13,
Issue. 1,
p.
64.
Forchini, G.
2000.
The density of the sufficient statistics for a Gaussian AR(1) model in terms of generalized functions.
Statistics & Probability Letters,
Vol. 50,
Issue. 3,
p.
237.
Forchini, G.
2005.
The Distribution of a Ratio of Quadratic Forms in Noncentral Normal Variables.
Communications in Statistics - Theory and Methods,
Vol. 34,
Issue. 5,
p.
999.
Bao, Yong
and
Ullah, Aman
2007.
Finite sample properties of maximum likelihood estimator in spatial models.
Journal of Econometrics,
Vol. 137,
Issue. 2,
p.
396.
Kan, Raymond
Wang, Xiaolu
and
Hillier, Grant
2007.
Computationally Efficient Recursions for Top-Order Invariant Polynomials with Applications.
SSRN Electronic Journal,
Hillier, Grant
Kan, Raymond
and
Wang, Xiaolu
2009.
Generating Functions and Short Recursions, with Applications to the Moments of Quadratic Forms in Noncentral Normal Vectors.
SSRN Electronic Journal,
Hillier, Grant
Kan, Raymond
and
Wang, Xiaolu
2009.
COMPUTATIONALLY EFFICIENT RECURSIONS FOR TOP-ORDER INVARIANT POLYNOMIALS WITH APPLICATIONS.
Econometric Theory,
Vol. 25,
Issue. 1,
p.
211.
Bao, Yong
and
Kan, Raymond
2013.
On the moments of ratios of quadratic forms in normal random variables.
Journal of Multivariate Analysis,
Vol. 117,
Issue. ,
p.
229.
Hillier, Grant
Kan, Raymond
and
Wang, Xiaolu
2014.
GENERATING FUNCTIONS AND SHORT RECURSIONS, WITH APPLICATIONS TO THE MOMENTS OF QUADRATIC FORMS IN NONCENTRAL NORMAL VECTORS.
Econometric Theory,
Vol. 30,
Issue. 2,
p.
436.
Caro-Lopera, Francisco J.
González Farías, Graciela
and
Balakrishnan, N.
2022.
Matrix Variate Distribution Theory under Elliptical Models—V: The Non-Central Wishart and Inverted Wishart Distributions.
Mathematical Methods of Statistics,
Vol. 31,
Issue. 1,
p.
18.
Watanabe, Junya
2023.
Exact expressions and numerical evaluation of average evolvability measures for characterizing and comparing $$\textbf{G}$$ matrices.
Journal of Mathematical Biology,
Vol. 86,
Issue. 6,
Watanabe, Junya
2023.
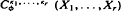 (Davis [8] and Chikuse [2] with r(r ≥ 2) symmetric matrix arguments have been defined, extending the zonal polynomials, and applied in multivariate distribution theory. The usefulness of the polynomials has attracted the attention of econometricians, and some recent papers have applied the methods to distribution theory in econometrics (e.g., Hillier [14] and Phillips [22]).
(Davis [8] and Chikuse [2] with r(r ≥ 2) symmetric matrix arguments have been defined, extending the zonal polynomials, and applied in multivariate distribution theory. The usefulness of the polynomials has attracted the attention of econometricians, and some recent papers have applied the methods to distribution theory in econometrics (e.g., Hillier [14] and Phillips [22]).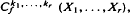 , in which each of the partitions of ki 1 = 1,…,r, and
, in which each of the partitions of ki 1 = 1,…,r, and 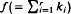 has only one part, occur frequently in multivariate distribution theory (e.g., Hillier and Satchell [17] and Phillips [27]). In this paper we give three methods of constructing these polynomials, extending those of Ruben [28] for the top order zonal polynomials. The first two methods yield explicit formulae for the polynomials and then we give a recurrence procedure. It is shown that some of the expansions presented in Chikuse and Davis [4] are simplified for the top order invariant polynomials. A brief discussion is given on the ‘lowest order’ invariant polynomials.
has only one part, occur frequently in multivariate distribution theory (e.g., Hillier and Satchell [17] and Phillips [27]). In this paper we give three methods of constructing these polynomials, extending those of Ruben [28] for the top order zonal polynomials. The first two methods yield explicit formulae for the polynomials and then we give a recurrence procedure. It is shown that some of the expansions presented in Chikuse and Davis [4] are simplified for the top order invariant polynomials. A brief discussion is given on the ‘lowest order’ invariant polynomials.