Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Granger, Clive W.J.
and
Haldrup, Niels
1996.
Separation in Cointegrated Systems, Long Memory Components and Common Stochastic Trends.
SSRN Electronic Journal ,
Granger, C. W. J.
and
Swanson, Norman
1996.
FUTURE DEVELOPMENTS IN THE STUDY OF COINTEGRATED VARIABLES*.
Oxford Bulletin of Economics and Statistics,
Vol. 58,
Issue. 3,
p.
537.
Ribba, Antonio
1997.
A note on the equivalence of long-run and short-run identifying restrictions in cointegration systems.
Economics Letters,
Vol. 56,
Issue. 3,
p.
273.
Swanson, Norman R.
1998.
Money and output viewed through a rolling window.
Journal of Monetary Economics,
Vol. 41,
Issue. 3,
p.
455.
Scorcu, Antonello E
and
Cellini, Roberto
1998.
Economic activity and crime in the long run: an empirical investigation on aggregate data from Italy, 1951–1994.
International Review of Law and Economics,
Vol. 18,
Issue. 3,
p.
279.
Caporale, G.M
and
Pittis, N
1998.
Cointegration and predictability of asset prices.
Journal of International Money and Finance,
Vol. 17,
Issue. 3,
p.
441.
Caporale, Guglielmo Maria
Hassapis, Christis
and
Pittis, Nikitas
1998.
Unit roots and long-run causality: investigating the relationship between output, money and interest rates.
Economic Modelling,
Vol. 15,
Issue. 1,
p.
91.
CROWDER, WILLIAM J.
1998.
THE LONG‐RUN LINK BETWEEN MONEY GROWTH AND INFLATION.
Economic Inquiry,
Vol. 36,
Issue. 2,
p.
229.
Freiwald, Winrich A.
Valdes, Pedro
Bosch, Jorge
Biscay, Rolando
Jimenez, Juan Carlos
Rodriguez, Luis Manuel
Rodriguez, Valia
Kreiter, Andreas K.
and
Singer, Wolf
1999.
Testing non-linearity and directedness of interactions between neural groups in the macaque inferotemporal cortex.
Journal of Neuroscience Methods,
Vol. 94,
Issue. 1,
p.
105.
Cheung, Yin-Wong
and
Westermann, Frank
1999.
An analysis of German effects on the Austrian business cycle.
Weltwirtschaftliches Archiv,
Vol. 135,
Issue. 3,
p.
522.
Gisser, Mica
1999.
DYNAMIC GAINS AND STATIC LOSSES IN OLIGOPOLY: EVIDENCE FROM THE BEER INDUSTRY.
Economic Inquiry,
Vol. 37,
Issue. 3,
p.
554.
Kuiper, W. Erno
Lutz, Clemens
and
van Tilburg, Aad
2000.
Agricultural Markets Beyond Liberalization.
p.
159.
Yao, Feng
and
Hosoya, Yuzo
2000.
Inference on one-way effect and evidence in Japanese macroeconomic data.
Journal of Econometrics,
Vol. 98,
Issue. 2,
p.
225.
Pesaran, M.Hashem
Shin, Yongcheol
and
Smith, Richard J.
2000.
Structural analysis of vector error correction models with exogenous I(1) variables.
Journal of Econometrics,
Vol. 97,
Issue. 2,
p.
293.
Hecq, Alain
Palm, Franz C.
and
Urbain, Jean-Pierre
2000.
Nonstationary Panels, Panel Cointegration, and Dynamic Panels.
Vol. 15,
Issue. ,
p.
131.
Heimonen, Kari
2001.
Substituting a Substitute Currency: The Case of Estonia.
SSRN Electronic Journal,
Pesaran, M. Hashem
Shin, Yongcheol
and
Smith, Richard J.
2001.
Bounds testing approaches to the analysis of level relationships.
Journal of Applied Econometrics,
Vol. 16,
Issue. 3,
p.
289.
Dekle, Robert
Hsiao, Cheng
and
Wang, Siyan
2001.
The Real Effects of Capital Inflows on Emerging Markets.
Review of Pacific Basin Financial Markets and Policies,
Vol. 04,
Issue. 02,
p.
165.
Darrat, Ali F.
2002.
BUDGET BALANCE THROUGH SPENDING CUTS OR TAX ADJUSTMENTS?.
Contemporary Economic Policy,
Vol. 20,
Issue. 3,
p.
221.
Cheung, Yin‐Wong
2002.
Hong Kong Output Dynamics: An Empirical Analysis.
Pacific Economic Review,
Vol. 7,
Issue. 3,
p.
465.
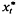 generated by
generated by 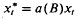 , where xt, and
, where xt, and 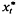 are both stationary, with finite variances and a(B) is a backward filter
are both stationary, with finite variances and a(B) is a backward filter


