Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T05:17:44.520Z Has data issue: false hasContentIssue false
  • English
  • Français

XX.—On General Differentiation. Part III

Published online by Cambridge University Press:  17 January 2013

P. Kelland
P. Kelland
Affiliation:
Late Fellow of Queen's College, Cambridge; Professor of Mathematics, &c., in the University of Edinburgh
Get access Rights & Permissions [Opens in a new window]

Extract

Nearly six years ago, I presented to the Society two Memoirs on the subject of Differentiation, with fractional indices. The method which I adopted to extend the signification of a differential coefficient consisted in assuming that the function 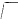, which enters into the value of the coefficient deduced from a particular hypothesis, is limited only by the definition 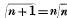. This generalization appears to be perfectly satisfactory, and promises to offer, if not the only, certainly the best extension of the Differential Calculus. Considering the length of the interval which has elapsed since the publication of my former Memoirs, it is remarkable that so little addition has been made to our knowledge of this branch of analysis. With the exception of one or two papers in Liouville's Journal, and a few remarks by Professor De Morgan, in his Treatise on the Differential Calculus (pp. 598–600), I am not aware that anything has been written on this subject since that time. Seeing, therefore, that others are not willing to enter on this very promising field, I consider it not improper that I should make known a number of extensions of this science to which I have been subsequently led, many of which have been in my possession a considerable time.

Type
Research Article
Information
Earth and Environmental Science Transactions of The Royal Society of Edinburgh , Volume 16 , Issue 3 , 1847 , pp. 241 - 303
Copyright
Copyright © Royal Society of Edinburgh 1847

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

page 242 note * See Part I., and the excellent Memoir of M. Liouville, referred to in that Treatise. Another formula has been proposed, viz.

I have lately received from Mr W. Center, of Langside, some judicious remarks on these formulæ, contrasting the results arrived at by them respectively. He shews that (without continual introduction of an infinite arbitrary constant) the latter formula is inapplicable in many of the most simple cases: for example, in dμ of expanded positively, it gives, when applied, infinity on one side and not on the other, and when expanded negatively, infinity on both sides; and again, it gives for or the value , which is a function of x when μ is a positive proper fraction.