Symplectomorphism groups and embeddings of balls into rational ruled 4-manifolds

Abstract

Let M_μ⁰ denote S²×S² endowed with a split symplectic form 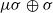normalized so that μ≥1 and σ(S²)=1. Given a symplectic embedding 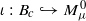of the standard ball of capacity c∈(0,1) into M_μ⁰, consider the corresponding symplectic blow-up 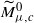. In this paper, we study the homotopy type of the symplectomorphism group 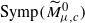and that of the space 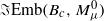of unparametrized symplectic embeddings of B_c into M_μ⁰. Writing ℓ for the largest integer strictly smaller than μ, and λ∈(0,1] for the difference μ−ℓ, we show that the symplectomorphism group of a blow-up of ‘small’ capacity c<λ is homotopically equivalent to the stabilizer of a point in Symp(M_μ⁰), while that of a blow-up of ‘large’ capacity c≥λ is homotopically equivalent to the stabilizer of a point in the symplectomorphism group of a non-trivial bundle 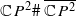obtained by blowing down 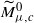. It follows that, for c<λ, the space 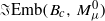is homotopy equivalent to S² ×S², while, for c≥λ, it is not homotopy equivalent to any finite CW-complex. A similar result holds for symplectic ruled manifolds diffeomorphic to 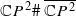. By contrast, we show that the embedding spaces 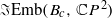and 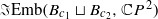, if non-empty, are always homotopy equivalent to the spaces of ordered configurations 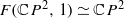and 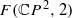. Our method relies on the theory of pseudo-holomorphic curves in 4 -manifolds, on the computation of Gromov invariants in rational 4 -manifolds, and on the inflation technique of Lalonde and McDuff.