Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-23T21:35:22.269Z Has data issue: false hasContentIssue false
  • English
  • Français

Stratifications with respect to actions of real reductive groups

Part of: Automorphic functions Complex spaces with a group of automorphisms

Published online by Cambridge University Press:  01 January 2008

Peter Heinzner ,
Gerald W. Schwarz  and
Henrik Stötzel
Peter Heinzner
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstrasse 150, D-44780 Bochum, Germany (email: [email protected], [email protected])
Gerald W. Schwarz
Affiliation:
Department of Mathematics, Brandeis University, PO Box 549110, Waltham, MA 02454-9110, USA (email: [email protected])
Henrik Stötzel
Affiliation:
Fakultät für Mathematik, Ruhr-Universität Bochum, Universitätsstrasse 150, D-44780 Bochum, Germany (email: [email protected], [email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

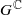We study the action of a real reductive group G on a real submanifold X of a Kähler manifold Z. We suppose that the action of G extends holomorphically to an action of the complexified group and that with respect to a compatible maximal compact subgroup U of 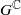the action on Z is Hamiltonian. There is a corresponding gradient map 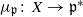where 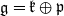is a Cartan decomposition of 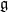. We obtain a Morse-like function 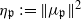on X. Associated with critical points of 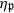are various sets of semistable points which we study in great detail. In particular, we have G-stable submanifolds Sβ of X which are called pre-strata. In cases where 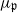is proper, the pre-strata form a decomposition of X and in cases where X is compact they are the strata of a Morse-type stratification of X. Our results are generalizations of results of Kirwan obtained in the case where 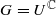and X=Z is compact.

Keywords

Cartan decompositionHamiltonian actionmoment mapstratification

MSC classification

Secondary: 32M05: Complex Lie groups, automorphism groups acting on complex spaces
Type
Research Article
Information
Compositio Mathematica , Volume 144 , Issue 1 , January 2008 , pp. 163 - 185
Copyright
Copyright © Foundation Compositio Mathematica 2008

References

The first author is partially supported by the Sonderforschungsbereich SFB/TR12 of the Deutsche Forschungsgemeinschaft. The second author is partially supported by NSA Grant H98230-06-1-0023. The third author is supported by the Sonderforschungsbereich SFB/TR12 of the Deutsche Forschungsgemeinschaft.