Stark–Heegner points and the Shimura correspondence

Abstract

Let 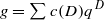and 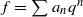be modular forms of half-integral weight k+1/2 and integral weight 2k respectively that are associated to each other under the Shimura–Kohnen correspondence. For suitable fundamental discriminants D, a theorem of Waldspurger relates the coefficient c(D) to the central critical value L(f,D,k) of the Hecke L-series of f twisted by the quadratic Dirichlet character of conductor D. This paper establishes a similar kind of relationship for central critical derivatives in the special case k=1, where f is of weight 2. The role of c(D) in our main theorem is played by the first derivative in the weight direction of the Dth Fourier coefficient of a p-adic family of half-integral weight modular forms. This family arises naturally, and is related under the Shimura correspondence to the Hida family interpolating f in weight 2. The proof of our main theorem rests on a variant of the Gross–Kohnen–Zagier formula for Stark–Heegner points attached to real quadratic fields, which may be of some independent interest. We also formulate a more general conjectural formula of Gross–Kohnen–Zagier type for Stark–Heegner points, and present numerical evidence for it in settings that seem inaccessible to our methods of proof based on p-adic deformations of modular forms.