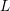Hostname: page-component-745bb68f8f-d8cs5 Total loading time: 0 Render date: 2025-02-08T20:57:22.776Z Has data issue: false hasContentIssue false
  • English
  • Français

The spin $L$-function on 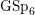$\text{GSp}_{6}$ for Siegel modular forms

Part of: Lie groups Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  10 May 2017

Aaron Pollack
Aaron Pollack*
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give a Rankin–Selberg integral representation for the Spin (degree eight) 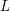$L$-function on 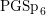$\operatorname{PGSp}_{6}$ that applies to the cuspidal automorphic representations associated to Siegel modular forms. If $\unicode[STIX]{x1D70B}$ corresponds to a level-one Siegel modular form 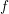$f$ of even weight, and if 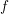$f$ has a nonvanishing maximal Fourier coefficient (defined below), then we deduce the functional equation and finiteness of poles of the completed Spin 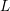$L$-function 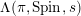$\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D70B},\text{Spin},s)$ of $\unicode[STIX]{x1D70B}$.

MSC classification

Primary: 11F66: Langlands $L$-functions; one variable Dirichlet series and functional equations 11F46: Siegel modular groups; Siegel and Hilbert-Siegel modular and automorphic forms
Secondary: 11F03: Modular and automorphic functions 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 7 , July 2017 , pp. 1391 - 1432
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andrianov, A. N., Dirichlet series with Euler product in the theory of Siegel modular forms of genus two , Trudy Mat. Inst. Steklov. 112 (1971), 73–94, 386.Google Scholar
Andrianov, A. N., Euler products that correspond to Siegel’s modular forms of genus 2 , Uspekhi Mat. Nauk 29 (1974), 43–110.Google Scholar
Asgari, M. and Schmidt, R., Siegel modular forms and representations , Manuscripta Math. 104 (2001), 173–200.Google Scholar
Bhargava, M. and Ho, W., Coregular spaces and genus one curves , Camb. J. Math. 4 (2016), 1–119.Google Scholar
Brandt, H., Idealtheorie in Quaternionenalgebren , Math. Ann. 99 (1928), 1–29.Google Scholar
Brown, R. B., Groups of type E 7 , J. Reine Angew. Math. 236 (1969), 79–102.Google Scholar
Brzeziński, J., A characterization of Gorenstein orders in quaternion algebras , Math. Scand. 50 (1982), 19–24.Google Scholar
Brzeziński, J., On orders in quaternion algebras , Comm. Algebra 11 (1983), 501–522.CrossRefGoogle Scholar
Bump, D., The Rankin–Selberg method: an introduction and survey , in Automorphic representations, L-functions and applications: progress and prospects, Ohio State University Mathematical Research Institute Publications, vol. 11 (de Gruyter, Berlin, 2005), 41–73.Google Scholar
Bump, D. and Ginzburg, D., Spin L-functions on symplectic groups , Int. Math. Res. Not. IMRN 1992 (1992), 153–160.CrossRefGoogle Scholar
Deligne, P., La série exceptionnelle de groupes de Lie , C. R. Acad. Sci. Paris Sér. I Math. 322 (1996), 321–326.Google Scholar
Deligne, P. and Gross, B. H., On the exceptional series, and its descendants , C. R. Math. Acad. Sci. Paris 335 (2002), 877–881.Google Scholar
Deligne, P. and de Man, R., La série exceptionnelle de groupes de Lie. II , C. R. Acad. Sci. Paris Sér. I Math. 323 (1996), 577–582.Google Scholar
Eichler, M., Quadratische Formen und orthogonale Gruppen, Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen mit besonderer Berücksichtigung der Anwendungsgebiete, vol. 63 (Springer, Berlin, 1952).Google Scholar
Evdokimov, S. A., Dirichlet series, multiple Andrianov zeta-functions in the theory of Euler modular forms of genus 3 , Dokl. Akad. Nauk SSSR 277 (1984), 25–29.Google Scholar
Faraut, J. and Korányi, A., Analysis on symmetric cones, Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 1994).Google Scholar
Freudenthal, H., Beziehungen der E 7 und E 8 zur Oktavenebene. I , Indag. Math. (N.S.) 16 (1954), 218–230; Nederl. Akad. Wetensch. Proc. Ser. A, vol. 57.Google Scholar
Furusawa, M., On L-functions for GSp(4) × GL(2) and their special values , J. Reine Angew. Math. 438 (1993), 187–218.Google Scholar
Gan, W. T. and Savin, G., On minimal representations definitions and properties , Represent. Theory 9 (2005), 46–93 (electronic).CrossRefGoogle Scholar
Garrett, P. B., Decomposition of Eisenstein series: Rankin triple products , Ann. of Math. (2) 125 (1987), 209–235.CrossRefGoogle Scholar
Gelbart, S., Piatetski-Shapiro, I. and Rallis, S., Explicit constructions of automorphic L-functions, Lecture Notes in Mathematics, vol. 1254 (Springer, Berlin, 1987).Google Scholar
Ginzburg, D. and Rallis, S., A tower of Rankin–Selberg integrals , Int. Math. Res. Not. IMRN 1994 (1994), 201–208 (electronic).Google Scholar
Gross, B. H. and Lucianovic, M. W., On cubic rings and quaternion rings , J. Number Theory 129 (2009), 1468–1478.Google Scholar
Langlands, R. P., Euler products, James K. Whittemore lectures in mathematics given at Yale University, Yale Mathematical Monographs, vol. 1 (Yale University Press, New Haven, CT, 1971).Google Scholar
Langlands, R. P., On the functional equations satisfied by Eisenstein series, Lecture Notes in Mathematics, vol. 544 (Springer, Berlin, 1976).Google Scholar
Lucianovic, M. W., Quaternion rings, ternary quadratic forms, and Fourier coefficients of modular forms on PGSp(6), PhD Thesis, Harvard University (2003).Google Scholar
Maass, H., Siegel’s modular forms and Dirichlet series, Lecture Notes in Mathematics, vol. 216 (Springer, Berlin, 1971).Google Scholar
Piatetski-Shapiro, I. and Rallis, S., Rankin triple L functions , Compos. Math. 64 (1987), 31–115.Google Scholar
Pollack, A. and Shah, S., The spin $L$ -function on $\text{GSp}_{6}$ via a non-unique model, Preprint (2015), arXiv:1503.08197.Google Scholar
Rumelhart, K. E., Minimal representations of exceptional p-adic groups , Represent. Theory 1 (1997), 133–181 (electronic).CrossRefGoogle Scholar
Saha, A., Siegel cusp forms of degree 2 are determined by their fundamental Fourier coefficients , Math. Ann. 355 (2013), 363–380.CrossRefGoogle Scholar
Shahidi, F., On the Ramanujan conjecture and finiteness of poles for certain L-functions , Ann. of Math. (2) 127 (1988), 547–584.Google Scholar
Shimura, G., Arithmetic of differential operators on symmetric domains , Duke Math. J. 48 (1981), 813–843.Google Scholar
Springer, T. A., Some groups of type E 7 , Nagoya Math. J. 182 (2006), 259–284.Google Scholar
Voight, J., Quaternion algebras, https://math.dartmouth.edu/∼jvoight/quat-book.pdf.Google Scholar
Voight, J., Characterizing quaternion rings over an arbitrary base , J. Reine Angew. Math. 657 (2011), 113–134.Google Scholar
Yamana, S., Determination of holomorphic modular forms by primitive Fourier coefficients , Math. Ann. 344 (2009), 853–862.Google Scholar
Yamana, S., On the Siegel–Weil formula for quaternionic unitary groups , Amer. J. Math. 135 (2013), 1383–1432.Google Scholar