Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-20T16:18:01.086Z Has data issue: false hasContentIssue false
  • English
  • Français

The real Chevalley involution

Part of: Algebraic number theory: global fields Lie groups

Published online by Cambridge University Press:  27 August 2014

Jeffrey Adams
Jeffrey Adams*
Affiliation:
University of Maryland, College Park, MD 20742-4015, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

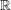The Chevalley involution of a connected, reductive algebraic group over an algebraically closed field takes every semisimple element to a conjugate of its inverse, and this involution is unique up to conjugacy. In the case of the reals we prove the existence of a real Chevalley involution, which is defined over $\mathbb{R}$, takes every semisimple element of 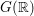$G(\mathbb{R})$ to a 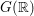$G(\mathbb{R})$-conjugate of its inverse, and is unique up to conjugacy by 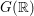$G(\mathbb{R})$. We derive some consequences, including an analysis of groups for which every irreducible representation is self-dual, and a calculation of the Frobenius Schur indicator for such groups.

Keywords

Chevalley involutionFrobenius Schur indicator

MSC classification

Primary: 22E50: Representations of Lie and linear algebraic groups over local fields 11R39: Langlands-Weil conjectures, nonabelian class field theory
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 12 , December 2014 , pp. 2127 - 2142
Copyright
© The Author 2014 

References

Adams, J. and du Cloux, F., Algorithms for representation theory of real reductive groups, J. Inst. Math. Jussieu 8 (2009), 209–259.Google Scholar
Adams, J. and Vogan, D. A. Jr, The contragredient, Preprint (2012), arXiv:1201.0496.Google Scholar
Borel, A. and Wallach, N., Continuous cohomology, discrete subgroups, and representations of reductive groups, Mathematical Surveys and Monographs, vol. 67, second edition (American Mathematical Society, Providence, RI, 2000).Google Scholar
Borel, A., Linear algebraic groups, Graduate Texts in Mathematics, vol. 126, second edition (Springer, New York, 1991).CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras. Chapters 7–9, Elements of Mathematics (Springer, Berlin, 2005), translated from the 1975 and 1982 French originals by Andrew Pressley.Google Scholar
Helgason, S., Differential geometry, Lie groups, and symmetric spaces, Graduate Studies in Mathematics, vol. 34 (American Mathematical Society, Providence, RI, 2001), corrected reprint of the 1978 original.Google Scholar
Helminck, A. G., Algebraic groups with a commuting pair of involutions and semisimple symmetric spaces, Adv. Math. 71 (1988), 21–91.Google Scholar
Helminck, A. G., On the classification of k-involutions, Adv. Math 153 (2000), 1–117.Google Scholar
Humphreys, J. E., Linear algebraic groups, Graduate Texts in Mathematics, vol. 21 (Springer, New York, 1975).Google Scholar
Knapp, A. W., Lie groups beyond an introduction, Progress in Mathematics, vol. 140, second edition (Birkhäuser, Boston, MA, 2002).Google Scholar
Knapp, A. W. and Vogan, D. A. Jr, Cohomological induction and unitary representations, Princeton Mathematical Series, vol. 45 (Princeton University Press, Princeton, NJ, 1995).CrossRefGoogle Scholar
Lusztig, G., Remarks on Springer’s representations, Represent. Theory 13 (2009), 391–400.Google Scholar
Mœglin, C., Vignéras, M.-F. and Waldspurger, J.-L., Correspondances de Howe sur un corps p-adique, Lecture Notes in Mathematics, vol. 1291 (Springer, Berlin, 1987).Google Scholar
Onishchik, A. L. and Vinberg, È. B., Lie groups and algebraic groups, Springer Series in Soviet Mathematics (Springer, Berlin, 1990), translated from the Russian and with a preface by D. A. Leites.Google Scholar
Prasad, D., A ‘relative’ local Langlands correspondence, Preprint.Google Scholar
Prasad, D., On the self-dual representations of a p-adic group, Internat. Math. Res. Notices 8 (1999), 443–452.CrossRefGoogle Scholar
Prasad, D. and Ramakrishnan, D., Self-dual representations of division algebras and Weil groups: a contrast, Amer. J. Math. 134 (2012), 749–767.Google Scholar
Springer, T. A., Linear algebraic groups, Progress in Mathematics, vol. 9, second edition (Birkhäuser, Boston, MA, 1998).CrossRefGoogle Scholar
Steinberg, R., Générateurs, relations et revêtements de groupes algébriques, in Colloq. Théorie des Groupes Algébriques (Bruxelles, 1962) (Librairie Universitaire, Louvain, 1962), 113–127.Google Scholar
Steinberg, R., Robert Steinberg collected works, Vol. 7 (American Mathematical Society, Providence, RI, 1997), edited and with a foreword by J.-P. Serre.Google Scholar
Vogan, D. A. Jr, Representations of real reductive Lie groups, Progress in Mathematics, vol. 15 (Birkhäuser, Boston, MA, 1981).Google Scholar
Vogan, D. A. Jr, Irreducible characters of semisimple Lie groups. IV. Character-multiplicity duality, Duke Math. J. 49 (1982), 943–1073.Google Scholar
Vogan, D. A. Jr, Unitary representations of reductive Lie groups, Annals of Mathematics Studies, vol. 118 (Princeton University Press, Princeton, NJ, 1987).Google Scholar
Vogan, D. A. Jr, Branching to a maximal compact subgroup, in Harmonic analysis, group representations, automorphic forms and invariant theory, Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 12 (World Scientific Publisher, Hackensack, NJ, 2007), 321–401.CrossRefGoogle Scholar