Published online by Cambridge University Press: 18 October 2018
Let 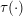 $\unicode[STIX]{x1D70F}(\cdot )$ be the classical Ramanujan
$\unicode[STIX]{x1D70F}(\cdot )$ be the classical Ramanujan  $\unicode[STIX]{x1D70F}$-function and let
$\unicode[STIX]{x1D70F}$-function and let 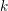 $k$ be a positive integer such that
$k$ be a positive integer such that 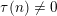 $\unicode[STIX]{x1D70F}(n)\neq 0$ for
$\unicode[STIX]{x1D70F}(n)\neq 0$ for 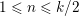 $1\leqslant n\leqslant k/2$. (This is known to be true for
$1\leqslant n\leqslant k/2$. (This is known to be true for 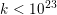 $k<10^{23}$, and, conjecturally, for all
$k<10^{23}$, and, conjecturally, for all 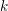 $k$.) Further, let
$k$.) Further, let  $\unicode[STIX]{x1D70E}$ be a permutation of the set
$\unicode[STIX]{x1D70E}$ be a permutation of the set 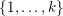 $\{1,\ldots ,k\}$. We show that there exist infinitely many positive integers
$\{1,\ldots ,k\}$. We show that there exist infinitely many positive integers 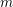 $m$ such that
$m$ such that 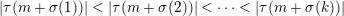 $|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(1))|<|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(2))|<\cdots <|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(k))|$. We also obtain a similar result for Hecke eigenvalues of primitive forms of square-free level.
$|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(1))|<|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(2))|<\cdots <|\unicode[STIX]{x1D70F}(m+\unicode[STIX]{x1D70E}(k))|$. We also obtain a similar result for Hecke eigenvalues of primitive forms of square-free level.