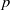Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T04:35:22.871Z Has data issue: false hasContentIssue false
  • English
  • Français

On the symbol length of $p$-algebras

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  22 May 2013

Mathieu Florence
Mathieu Florence*
Affiliation:
Equipe de Topologie et Géométrie Algébriques, Institut de Mathématiques de Jussieu, 4 place Jussieu, 75005 Paris, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The main result of this paper states that if 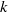$k$ is a field of characteristic 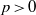$p\gt 0$ and 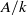$A/ k$ is a central simple algebra of index 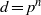$d= {p}^{n} $ and exponent 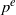${p}^{e} $, then 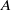$A$ is split by a purely inseparable extension of 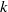$k$ of the form 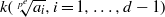$k( \sqrt[{p}^{e} ]{{a}_{i} }, i= 1, \ldots , d- 1)$. Combining this result with a theorem of Albert (for which we include a new proof), we get that any such algebra is Brauer equivalent to the tensor product of at most 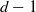$d- 1$ cyclic algebras of degree 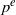${p}^{e} $. This gives a drastic improvement upon previously known upper bounds.

Keywords

central simple algebrasSeveri–Brauer varieties

MSC classification

Secondary: 20G15: Linear algebraic groups over arbitrary fields
Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1353 - 1363
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Albert, A. A., Structure of algebras, American Mathematical Society Colloquium Publications, vol. XXIV (American Mathematical Society, Providence, RI, 1939).Google Scholar
Auel, A., Brussel, E., Garibaldi, S. and Vishne, U., Open problems on central simple algebras, Transform. Groups 16 (2011), 219–264.Google Scholar
Florence, M., On the essential dimension of cyclic $p$-groups, Invent. Math. 171 (2008), 175–189.Google Scholar
Gabber, O., Some theorems on Azumaya algebras, in Groupe de Brauer, Lecture Notes in Mathematics, vol. 844 (Springer, Berlin, 1981), 129–209.CrossRefGoogle Scholar
Gille, P. and Szamuely, T., Central simple algebras and Galois cohomology (Cambridge University Press, Cambridge, 2006).Google Scholar
Jacobson, N., Finite-dimensional division algebras over fields (Springer, Berlin, 2010).Google Scholar
Knus, M.-A., Ojanguren, M. and Saltman, D., Brauer groups in characteristic $p$, in Brauer groups (Evanston, October 11–15, 1975), Lecture Notes in Mathematics, vol. 549 (Springer, Berlin, 1976).Google Scholar
Mammone, P., Sur la corestriction des $p$-symboles, Comm. Algebra 14 (1986), 517–529.CrossRefGoogle Scholar
Mammone, P. and Merkurjev, A., On the corestriction of ${p}^{n} $-symbol, Israel J. Math. 76 (1991), 73–79.CrossRefGoogle Scholar
Oesterlé, J., Nombres de Tamagawa et groupes unipotents en caractéristique $p$, Invent. Math. 78 (1984), 13–88.Google Scholar
Teichmüller, O., $p$-Algebren, Deutsche Mathematik 1 (1936), 362–388.Google Scholar