Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tang, Shun
2014.
Canonical key formula for projective abelian schemes.
Manuscripta Mathematica,
Vol. 145,
Issue. 3-4,
p.
255.
Moriwaki, Atsushi
2015.
Toward a geometric analogue of Dirichlet’s unit theorem.
Kyoto Journal of Mathematics,
Vol. 55,
Issue. 4,


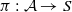 be an abelian scheme over a scheme
be an abelian scheme over a scheme 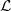 be a symmetric, rigidified, relatively ample line bundle on
be a symmetric, rigidified, relatively ample line bundle on 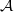 . We show that there is an isomorphism
. We show that there is an isomorphism 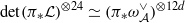
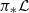 . We also show that the numbers 24 and 12
. We also show that the numbers 24 and 12