Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T05:07:57.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Large families of elliptic curves ordered by conductor

Part of: Algebraic number theory: global fields Arithmetic algebraic geometry Forms and linear algebraic groups

Published online by Cambridge University Press:  22 June 2021

Ananth N. Shankar ,
Arul Shankar  and
Xiaoheng Wang
Ananth N. Shankar
Affiliation:
Department of Mathematics, University of Wisconsin-Madison, Madison, WI53706, [email protected]
Arul Shankar
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ONM5S 2E4, [email protected]
Xiaoheng Wang
Affiliation:
Department of Pure Mathematics, University of Waterloo, Waterloo, ONN2L 3G1, [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study the family of elliptic curves 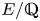$E/{{\mathbb {Q}}}$, having good reduction at 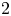$2$ and 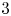$3$, and whose 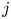$j$-invariants are small. Within this set of elliptic curves, we consider the following two subfamilies: first, the set of elliptic curves 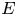$E$ such that the quotient 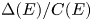$\Delta (E)/C(E)$ of the discriminant divided by the conductor is squarefree; and second, the set of elliptic curves 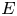$E$ such that the Szpiro quotient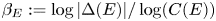$\beta _E:=\log |\Delta (E)|/\log (C(E))$ is less than 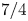$7/4$. Both these families are conjectured to contain a positive proportion of elliptic curves, when ordered by conductor. Our main results determine asymptotics for both these families, when ordered by conductor. Moreover, we prove that the average size of the 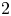$2$-Selmer groups of elliptic curves in the first family, again when these curves are ordered by their conductors, is 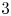$3$. The key new ingredients necessary for the proofs are ‘uniformity estimates’, namely upper bounds on the number of elliptic curves with bounded height, whose discriminants are divisible by high powers of primes.

Keywords

elliptic curvesconductordiscriminant

MSC classification

Primary: 11G05: Elliptic curves over global fields
Secondary: 11R29: Class numbers, class groups, discriminants 11R45: Density theorems 11E76: Forms of degree higher than two
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 7 , July 2021 , pp. 1538 - 1583
Check for updates
Copyright
© The Author(s) 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ash, A., Brakenhoff, J. and Zarrabi, T., Equality of polynomial and field discriminants, Exp. Math. 16 (2007), 367–374; MR 2367325.CrossRefGoogle Scholar
Barroero, F. and Widmer, M., Counting lattice points and O-minimal structures, Int. Math. Res. Not. IMRN 18 (2014), 4932–4957; MR 3264671.CrossRefGoogle Scholar
Bhargava, M., Higher composition laws. II. On cubic analogues of Gauss composition, Ann. of Math. (2) 159 (2004), 865–886.CrossRefGoogle Scholar
Bhargava, M., The density of discriminants of quartic rings and fields, Ann. of Math. (2) 162 (2005), 1031–1063.CrossRefGoogle Scholar
Bhargava, M., The geometric squarefree sieve and unramified nonabelian extensions of quadratic fields, Preprint (2014), arXiv:1402.0031.Google Scholar
Bhargava, M. and Harron, P., The equidistribution of lattice shapes of rings of integers in cubic, quartic, and quintic number fields, Compos. Math. 152 (2016), 1111–1120; MR 3518306.CrossRefGoogle Scholar
Bhargava, M. and Shankar, A., Binary quartic forms having bounded invariants, and the boundedness of the average rank of elliptic curves, Ann. of Math. (2) 181 (2015), 191–242; MR 3272925.CrossRefGoogle Scholar
Bhargava, M., Shankar, A., Taniguchi, T., Thorne, F., Tsimerman, J. and Zhao, Y., Bounds on 2-torsion in class groups of number fields and integral points on elliptic curves, Preprint (2017), arXiv:1701.02458.Google Scholar
Bhargava, M., Shankar, A. and Tsimerman, J., On the Davenport-Heilbronn theorems and second order terms, Invent. Math. 193 (2013), 439–499; MR 3090184.CrossRefGoogle Scholar
Bhargava, M., Shankar, A. and Wang, X., Geometry-of-numbers methods over global fields I: Prehomogeneous vector spaces, Preprint (2015), arXiv:1512.03035.Google Scholar
Bhargava, M., Shankar, A. and Wang, X., Squarefree values of polynomial discriminants I, Preprint (2016), arXiv:1611.09806.Google Scholar
Brumer, A., The average rank of elliptic curves. I, Invent. Math. 109 (1992), 445–472.CrossRefGoogle Scholar
Brumer, A. and Kramer, K., The rank of elliptic curves, Duke Math. J. 44 (1977), 715–743; MR 0457453.CrossRefGoogle Scholar
Brumer, A. and McGuinness, O., The behavior of the Mordell-Weil group of elliptic curves, Bull. Amer. Math. Soc. (N.S.) 23 (1990), 375–382.CrossRefGoogle Scholar
Chiche-Lapierre, V., Length of elements in a Minkowski basis for an order in a number field, PhD thesis, University of Toronto (2019).Google Scholar
Davenport, H., On a principle of Lipschitz, J. Lond. Math. Soc. 26 (1951), 179–183.CrossRefGoogle Scholar
Delone, B. N. and Faddeev, D. K., Theory of irrationalities of third degree, Acad. Sci. URSS. Trav. Inst. Math. Stekloff 11 (1940), 340; MR 0004269.Google Scholar
Duke, W. and Kowalski, E., A problem of Linnik for elliptic curves and mean-value estimates for automorphic representations, Invent. Math. 139 (2000), 1–39, with an appendix by Dinakar Ramakrishnan; MR 1728875.CrossRefGoogle Scholar
Eskin, A. and Katznelson, R. Y., Singular symmetric matrices, Duke Math. J. 79 (1995), 515–547.CrossRefGoogle Scholar
Fouvry, É., Nair, M. and Tenenbaum, G., L'ensemble exceptionnel dans la conjecture de Szpiro, Bull. Soc. Math. France 120 (1992), 485–506; MR 1194273.CrossRefGoogle Scholar
Fujiwara, M., Über die obere Schranke des absoluten Betrages der Wurzeln einer algebraischen Gleichung, Tohoku Math. J., First Series 10 (1916), 167–171.Google Scholar
Gan, W. T., Gross, B. and Savin, G., Fourier coefficients of modular forms on $G_2$, Duke Math. J. 115 (2002), 105–169; MR 1932327.CrossRefGoogle Scholar
Goldfeld, D., Conjectures on elliptic curves over quadratic fields, in Number theory, Carbondale 1979 Proceedings of the Southern Illinois Number Theory Conference Carbondale, Southern Illinois University, Carbondale, IL, 1979, Lecture Notes in Mathematics, vol. 751 (Springer, Berlin, 1979), 108–118.CrossRefGoogle Scholar
Heath-Brown, D. R., The average analytic rank of elliptic curves, Duke Math. J. 122 (2004), 591–623.CrossRefGoogle Scholar
Hortsch, R., Counting elliptic curves of bounded Faltings height, Acta Arith. 173 (2016), 239–253; MR 3512854.Google Scholar
Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy, American Mathematical Society Colloquium Publications, vol. 45 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Levi, F., Kubische Zahlkörper und binare kubische Formenklassen, Ber. Sächs. Akad. Wiss. Leipz., Mat.-Nat. Kl. 66 (1914), 26–37.Google Scholar
Oesterlé, J., in Nouvelles approches du théorème de fermat, in Séminaire Bourbaki: volume 1987/88, exposés 686-699, Astérisque, vol. 161–162 (Société Mathématique de France, 1988), 165–186; MR 992208.Google Scholar
Silverman, J. H., Advanced topics in the arithmetic of elliptic curves, Graduate Texts in Mathematics, vol. 151 (Springer, New York, 1994); MR 1312368.CrossRefGoogle Scholar
Taniguchi, T. and Thorne, F., Levels of distribution for sieve problems in prehomogeneous vector spaces, Math. Ann. 376 (2020), 1537–1559.CrossRefGoogle Scholar
Watkins, M., Some heuristics about elliptic curves, Exp. Math. 17 (2008), 105–125.CrossRefGoogle Scholar
Wilkie, A. J., Model completeness results for expansions of the ordered field of real numbers by restricted Pfaffian functions and the exponential function, J. Amer. Math. Soc. 9 (1996), 1051–1094.CrossRefGoogle Scholar
Young, M. P., Low-lying zeros of families of elliptic curves, J. Amer. Math. Soc. 19 (2006), 205–250.CrossRefGoogle Scholar