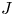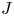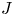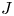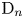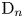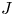1. Introduction
Chow motives were introduced by Grothendieck, and since then they have become a fundamental tool for investigating the structure of algebraic varieties. The study of Chow motives and motivic decompositions has several outstanding applications to other topics. For example, Voevodsky's proof of the Milnor conjecture relied on Rost's computation of the motivic decomposition of a Pfister quadric. In [Reference KarpenkoKar10] Karpenko established the relation between the motivic decomposition and the canonical dimension of a projective homogeneous variety, which allowed the canonical dimension to be computed in many cases.
In [Reference Petrov, Semenov and ZainoullinePSZ08] Petrov, Semenov, and Zainoulline investigated the structure of the motives of generically split projective homogeneous varieties and introduced a new invariant of an algebraic group ![]() $G$, called the
$G$, called the ![]() $J$-invariant. In the case of quadratic forms the
$J$-invariant. In the case of quadratic forms the ![]() $J$-invariant was introduced previously by Vishik in [Reference VishikVis05]. For a fixed prime number
$J$-invariant was introduced previously by Vishik in [Reference VishikVis05]. For a fixed prime number ![]() $p$ the
$p$ the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ modulo
$G$ modulo ![]() $p$ is a discrete invariant consisting of several non-negative integer components
$p$ is a discrete invariant consisting of several non-negative integer components ![]() $(j_1,\ldots, j_r)$ with degrees
$(j_1,\ldots, j_r)$ with degrees ![]() $1\leq d_1\leq \cdots \leq d_r$. The integers
$1\leq d_1\leq \cdots \leq d_r$. The integers ![]() $r$ and
$r$ and ![]() $d_1, \ldots d_r$ depend only on the type of
$d_1, \ldots d_r$ depend only on the type of ![]() $G$ and are known for all types (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). The
$G$ and are known for all types (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). The ![]() $J$-invariant encodes the motivic decomposition of the variety
$J$-invariant encodes the motivic decomposition of the variety ![]() $X$ of Borel subgroups in
$X$ of Borel subgroups in ![]() $G$. More precisely, it turns out that the Chow motive of
$G$. More precisely, it turns out that the Chow motive of ![]() $X$ with coefficients in
$X$ with coefficients in ![]() $\mathbb {F}_p$ decomposes into a direct sum of Tate twists of an indecomposable motive
$\mathbb {F}_p$ decomposes into a direct sum of Tate twists of an indecomposable motive ![]() $\mathcal {R}_p(G)$ and the Poincaré polynomial of
$\mathcal {R}_p(G)$ and the Poincaré polynomial of ![]() $\mathcal {R}_p(G)$ over a splitting field of
$\mathcal {R}_p(G)$ over a splitting field of ![]() $G$ equals
$G$ equals
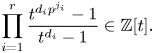 \begin{equation} \prod_{i=1}^r\frac{t^{d_ip^{j_i}}-1}{t^{d_i}-1}\in\mathbb{Z}[t]. \end{equation}
\begin{equation} \prod_{i=1}^r\frac{t^{d_ip^{j_i}}-1}{t^{d_i}-1}\in\mathbb{Z}[t]. \end{equation} The ![]() $J$-invariant proved to be an important tool for solving several long-standing problems. For example, it plays an important role in the progress on the Kaplansky problem about possible values of the
$J$-invariant proved to be an important tool for solving several long-standing problems. For example, it plays an important role in the progress on the Kaplansky problem about possible values of the ![]() $u$-invariant, see [Reference VishikVis09]. Another example is the proof of a conjecture of Serre about groups of type
$u$-invariant, see [Reference VishikVis09]. Another example is the proof of a conjecture of Serre about groups of type ![]() $\mathrm {E}_8$ and its finite subgroups, where the
$\mathrm {E}_8$ and its finite subgroups, where the ![]() $J$-invariant plays a crucial role (see [Reference Garibaldi and SemenovGS10, Reference SemenovSem16]). More recently, Petrov and Semenov generalized the
$J$-invariant plays a crucial role (see [Reference Garibaldi and SemenovGS10, Reference SemenovSem16]). More recently, Petrov and Semenov generalized the ![]() $J$-invariant for groups of inner type to arbitrary oriented cohomology theories in the sense of Levine and Morel [Reference Levine and MorelLM07] satisfying some axioms (see [Reference Petrov and SemenovPS21]).
$J$-invariant for groups of inner type to arbitrary oriented cohomology theories in the sense of Levine and Morel [Reference Levine and MorelLM07] satisfying some axioms (see [Reference Petrov and SemenovPS21]).
Let ![]() $(A,\sigma )$ be a central simple algebra of even degree
$(A,\sigma )$ be a central simple algebra of even degree ![]() $2n$, endowed with an involution of orthogonal type and trivial discriminant. Let
$2n$, endowed with an involution of orthogonal type and trivial discriminant. Let ![]() $G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$ be the connected component of the automorphism group of
$G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$ be the connected component of the automorphism group of ![]() $(A, \sigma )$. The group
$(A, \sigma )$. The group ![]() $G$ is adjoint of type
$G$ is adjoint of type ![]() $\mathrm {D}_n$. Denote by
$\mathrm {D}_n$. Denote by ![]() $J(G) = (j_1,\ldots, j_r)$ the
$J(G) = (j_1,\ldots, j_r)$ the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ modulo
$G$ modulo ![]() $p=2$. It is known that the first component
$p=2$. It is known that the first component ![]() $j_1$ is zero if the algebra
$j_1$ is zero if the algebra ![]() $A$ is split. In particular,
$A$ is split. In particular, ![]() $j_1$ becomes zero over the function field
$j_1$ becomes zero over the function field ![]() $F_A$ of the Severi–Brauer variety of
$F_A$ of the Severi–Brauer variety of ![]() $A$, which is a generic splitting field of
$A$, which is a generic splitting field of ![]() $A$.
$A$.
In [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12] Quéguiner-Mathieu, Semenov, and Zainoulline stated a conjecture that the remaining components do not change after generic splitting of ![]() $A$.
$A$.
Conjecture 1.2 [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Remark 7.3]
If ![]() $J(G)=(j_1,\ldots, j_r)$, then
$J(G)=(j_1,\ldots, j_r)$, then ![]() $j_i=(j_i)_{F_A}$ for
$j_i=(j_i)_{F_A}$ for ![]() $i=2,\ldots,r$.
$i=2,\ldots,r$.
Note that, in the settings of Conjecture 1.2 the central simple algebra ![]() $A$ is a Tits algebra of the algebraic group
$A$ is a Tits algebra of the algebraic group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$. In the present paper we prove Conjecture 1.2 and, moreover, generalize it to the case of an arbitrary semisimple algebraic group
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$. In the present paper we prove Conjecture 1.2 and, moreover, generalize it to the case of an arbitrary semisimple algebraic group ![]() $G$ of inner type. Let
$G$ of inner type. Let ![]() $A$ be a Tits algebra of
$A$ be a Tits algebra of ![]() $G$. The main result of the paper (Theorem 4.1) describes the connection between the
$G$. The main result of the paper (Theorem 4.1) describes the connection between the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ over a generic splitting field of
$G$ over a generic splitting field of ![]() $A$ and the
$A$ and the ![]() $J$-invariant over a base field. In particular, we prove that all components of the
$J$-invariant over a base field. In particular, we prove that all components of the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ of degree greater than
$G$ of degree greater than ![]() $1$ do not change after extending to a generic splitting field
$1$ do not change after extending to a generic splitting field ![]() $F_A$ of
$F_A$ of ![]() $A$. Moreover, the main theorem provides some control on how the components of degree
$A$. Moreover, the main theorem provides some control on how the components of degree ![]() $1$ can change over the field
$1$ can change over the field ![]() $F_A$. In the case
$F_A$. In the case ![]() $G=\operatorname {\mathrm {PGO}}^+(A,\sigma )$ we improve this control in Proposition 5.1, which together with the main theorem allows us to prove Conjecture 1.2 (see Corollary 5.3).
$G=\operatorname {\mathrm {PGO}}^+(A,\sigma )$ we improve this control in Proposition 5.1, which together with the main theorem allows us to prove Conjecture 1.2 (see Corollary 5.3).
The main result of the paper allows us to split a Tits algebra of an algebraic group without losing much information on the ![]() $J$-invariant of the group (only components of degree one may be affected). This may be a useful tool to compute the
$J$-invariant of the group (only components of degree one may be affected). This may be a useful tool to compute the ![]() $J$-invariant, since the algebraic groups with trivial Tits algebras are considered as ‘less complex objects’ compared with those groups with non-trivial Tits algebras. For example, in the settings of Conjecture 1.2 the group
$J$-invariant, since the algebraic groups with trivial Tits algebras are considered as ‘less complex objects’ compared with those groups with non-trivial Tits algebras. For example, in the settings of Conjecture 1.2 the group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$ over the field
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$ over the field ![]() $F_A$ becomes isomorphic to
$F_A$ becomes isomorphic to ![]() $\operatorname {\mathrm {PGO}}^+(q_{\sigma })$, where
$\operatorname {\mathrm {PGO}}^+(q_{\sigma })$, where ![]() $q_{\sigma }$ is the respective quadratic form adjoint to the split algebra with involution
$q_{\sigma }$ is the respective quadratic form adjoint to the split algebra with involution ![]() $(A, \sigma )_{F_A}$. Hence, Conjecture 1.2 allows the computation of the
$(A, \sigma )_{F_A}$. Hence, Conjecture 1.2 allows the computation of the ![]() $J$-invariant (except the first component) of algebras with orthogonal involution to be reduced to the case of quadratic forms. Note that recently a similar approach was used to investigate the motivic equivalence of algebras with involutions, see [Reference De Clercq, Quéguiner-Mathieu and ZhykhovichDQZ22].
$J$-invariant (except the first component) of algebras with orthogonal involution to be reduced to the case of quadratic forms. Note that recently a similar approach was used to investigate the motivic equivalence of algebras with involutions, see [Reference De Clercq, Quéguiner-Mathieu and ZhykhovichDQZ22].
Section 5 of the paper is devoted to the computation of the first two components ![]() $j_1$ and
$j_1$ and ![]() $j_2$ of the
$j_2$ of the ![]() $J$-invariant of the group
$J$-invariant of the group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$ of type
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$ of type ![]() $\mathrm {D}_n$, where
$\mathrm {D}_n$, where ![]() $(A, \sigma )$ is a central simple algebra with orthogonal involution. This question was already investigated in [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12]. Namely, in [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] the upper bounds for
$(A, \sigma )$ is a central simple algebra with orthogonal involution. This question was already investigated in [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12]. Namely, in [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] the upper bounds for ![]() $j_1$ and
$j_1$ and ![]() $j_2$ were provided in terms of
$j_2$ were provided in terms of ![]() $2$-adic valuations
$2$-adic valuations ![]() $i_A$,
$i_A$, ![]() $i_+$, and
$i_+$, and ![]() $i_-$ of indices of algebras
$i_-$ of indices of algebras ![]() $A$,
$A$, ![]() $C_+$, and
$C_+$, and ![]() $C_-$, respectively, where
$C_-$, respectively, where ![]() $C_+$ and
$C_+$ and ![]() $C_-$ are the components of the Clifford algebra of
$C_-$ are the components of the Clifford algebra of ![]() $(A, \sigma )$. We improve the upper bound for
$(A, \sigma )$. We improve the upper bound for ![]() $j_1$ and then show that it is, in fact, the exact value of
$j_1$ and then show that it is, in fact, the exact value of ![]() $j_1$ (see Theorem 5.9). More precisely, we obtain the following formula
$j_1$ (see Theorem 5.9). More precisely, we obtain the following formula
where ![]() $k_1$ denotes the
$k_1$ denotes the ![]() $2$-adic valuation of
$2$-adic valuation of ![]() $n$.
$n$.
Note that the formula for ![]() $j_1$ and Conjecture 1.2 (Corollary 5.3) allow us to completely reduce the computation of the
$j_1$ and Conjecture 1.2 (Corollary 5.3) allow us to completely reduce the computation of the ![]() $J$-invariant of the group
$J$-invariant of the group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$ to the case of quadratic forms. Moreover, in Proposition 5.14 we also provide an explicit formula for the second component
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$ to the case of quadratic forms. Moreover, in Proposition 5.14 we also provide an explicit formula for the second component ![]() $j_2$ in some cases.
$j_2$ in some cases.
Note that recently Henke in his PhD thesis [Reference HenkeHen22] applied the main result of this paper to investigate motivic decompositions of projective homogeneous varieties for groups of type ![]() $\mathrm {E}_7$.
$\mathrm {E}_7$.
The proofs in this paper rely on the computations of rational cycles, the properties of generically split varieties, the theory of upper motives and the index reduction formula.
2. Preliminaries and notation
2.1 Chow motives
Let ![]() $F$ be a field. In the present paper we work in the category of the Grothendieck–Chow motives over
$F$ be a field. In the present paper we work in the category of the Grothendieck–Chow motives over ![]() $F$ with coefficients in
$F$ with coefficients in ![]() $\mathbb {F}_p$ for a fixed prime number
$\mathbb {F}_p$ for a fixed prime number ![]() $p$ (see [Reference Elman, Karpenko and MerkurjevEKM08]).
$p$ (see [Reference Elman, Karpenko and MerkurjevEKM08]).
For a smooth projective variety ![]() $X$ over
$X$ over ![]() $F$ we denote by
$F$ we denote by ![]() $M(X)$ the motive of
$M(X)$ the motive of ![]() $X$ in this category. We consider the Chow ring
$X$ in this category. We consider the Chow ring ![]() $\mathop {\mathrm {CH}}\nolimits (X)$ of
$\mathop {\mathrm {CH}}\nolimits (X)$ of ![]() $X$ modulo rational equivalence and we write
$X$ modulo rational equivalence and we write ![]() $\mathop {\mathrm {Ch}}\nolimits (X)$ for the Chow ring with coefficients in
$\mathop {\mathrm {Ch}}\nolimits (X)$ for the Chow ring with coefficients in ![]() $\mathbb {F}_p$.
$\mathbb {F}_p$.
For a motive ![]() $M$ over
$M$ over ![]() $F$ and a field extension
$F$ and a field extension ![]() $E/F$ we denote by
$E/F$ we denote by ![]() $M_E$ the extension of scalars. A motive
$M_E$ the extension of scalars. A motive ![]() $M$ is called split (respectively, geometrically split), if it is isomorphic to a finite direct sum of Tate motives (respectively, if
$M$ is called split (respectively, geometrically split), if it is isomorphic to a finite direct sum of Tate motives (respectively, if ![]() $M_E$ is split over some field extension
$M_E$ is split over some field extension ![]() $E/F$).
$E/F$).
Let ![]() $G$ be a semisimple algebraic group of inner type. Let
$G$ be a semisimple algebraic group of inner type. Let ![]() $X$ be a projective homogeneous variety under the action of
$X$ be a projective homogeneous variety under the action of ![]() $G$. Note that the motive of
$G$. Note that the motive of ![]() $X$ splits over any field extension, over which the group
$X$ splits over any field extension, over which the group ![]() $G$ splits (in the sense of algebraic groups). By
$G$ splits (in the sense of algebraic groups). By ![]() $\overline {X}$ we denote the variety
$\overline {X}$ we denote the variety ![]() $X_E$ over a splitting field
$X_E$ over a splitting field ![]() $E$ of the group
$E$ of the group ![]() $G$. The Chow ring
$G$. The Chow ring ![]() $\mathop {\mathrm {CH}}\nolimits (\overline {X})$ does not depend on the choice of
$\mathop {\mathrm {CH}}\nolimits (\overline {X})$ does not depend on the choice of ![]() $E$ and, therefore, we do not specify the splitting fields in the formulas below. By
$E$ and, therefore, we do not specify the splitting fields in the formulas below. By ![]() $\overline {\mathop {\mathrm {CH}}\nolimits }(X)$ we denote the image of the restriction homomorphism
$\overline {\mathop {\mathrm {CH}}\nolimits }(X)$ we denote the image of the restriction homomorphism ![]() $\mathop {\mathrm {CH}}\nolimits (X) \rightarrow \mathop {\mathrm {CH}}\nolimits (\overline {X})$. We say that a cycle from
$\mathop {\mathrm {CH}}\nolimits (X) \rightarrow \mathop {\mathrm {CH}}\nolimits (\overline {X})$. We say that a cycle from ![]() $\mathop {\mathrm {CH}}\nolimits (\overline {X})$ is
$\mathop {\mathrm {CH}}\nolimits (\overline {X})$ is ![]() $F$-rational if it belongs to
$F$-rational if it belongs to ![]() $\overline {\mathop {\mathrm {CH}}\nolimits }(X)$.
$\overline {\mathop {\mathrm {CH}}\nolimits }(X)$.
The Poincaré polynomial ![]() $P(X,t)$ of
$P(X,t)$ of ![]() $X$ is defined as
$X$ is defined as ![]() $\sum _{i\geq 0} \dim \mathop {\mathrm {Ch}}\nolimits ^i(\overline {X}) t^i$. Similarly, for direct motivic summand
$\sum _{i\geq 0} \dim \mathop {\mathrm {Ch}}\nolimits ^i(\overline {X}) t^i$. Similarly, for direct motivic summand ![]() $M$ of
$M$ of ![]() $X$ we define the Poincaré polynomial
$X$ we define the Poincaré polynomial ![]() $P(M,t)$ by replacing
$P(M,t)$ by replacing ![]() $\overline {X}$ by
$\overline {X}$ by ![]() $\overline {M}$ in the formula, where
$\overline {M}$ in the formula, where ![]() $\overline {M}$ denotes the motive
$\overline {M}$ denotes the motive ![]() $M$ over a splitting field of
$M$ over a splitting field of ![]() $G$.
$G$.
Recall that the Krull–Schmidt principle holds for any motivic direct summand ![]() $M$ of a projective homogeneous variety
$M$ of a projective homogeneous variety ![]() $X$. Namely,
$X$. Namely, ![]() $M$ decomposes in a unique way in a finite direct sum of indecomposable motives, see [Reference Chernousov and MerkurjevCM06]. The upper motive
$M$ decomposes in a unique way in a finite direct sum of indecomposable motives, see [Reference Chernousov and MerkurjevCM06]. The upper motive ![]() $U(X)$ of
$U(X)$ of ![]() $X$ is defined as an indecomposable summand of
$X$ is defined as an indecomposable summand of ![]() $M(X)$ with the property that the Chow group
$M(X)$ with the property that the Chow group ![]() $\mathop {\mathrm {Ch}}\nolimits ^0(U(X))$ is non-zero. It follows by the Krull–Schmidt principle that the isomorphism class of
$\mathop {\mathrm {Ch}}\nolimits ^0(U(X))$ is non-zero. It follows by the Krull–Schmidt principle that the isomorphism class of ![]() $U(X)$ is uniquely determined by
$U(X)$ is uniquely determined by ![]() $X$.
$X$.
Given two projective homogeneous varieties ![]() $X_1$ and
$X_1$ and ![]() $X_2$ (under possibly different algebraic groups) over
$X_2$ (under possibly different algebraic groups) over ![]() $F$, the upper motives of the varieties
$F$, the upper motives of the varieties ![]() $X_1$ and
$X_1$ and ![]() $X_2$ satisfy the following isomorphism criterion.
$X_2$ satisfy the following isomorphism criterion.
Proposition 2.1 [Reference KarpenkoKar13, Corollary 2.15]
The upper motives ![]() $U(X_1)$ and
$U(X_1)$ and ![]() $U(X_2)$ are isomorphic if and only of the varieties
$U(X_2)$ are isomorphic if and only of the varieties ![]() $X_1$ and
$X_1$ and ![]() $X_2$ possesses
$X_2$ possesses ![]() $0$-cycles of degree
$0$-cycles of degree ![]() $1$ modulo
$1$ modulo ![]() $p$ over
$p$ over ![]() $F(X_2)$ and
$F(X_2)$ and ![]() $F(X_1)$, respectively.
$F(X_1)$, respectively.
2.2 Tits algebras and the Picard group
Let ![]() $G_0$ be a split semisimple algebraic group of inner type of rank
$G_0$ be a split semisimple algebraic group of inner type of rank ![]() $n$ over
$n$ over ![]() $F$. We fix a split maximum torus
$F$. We fix a split maximum torus ![]() $T$ in
$T$ in ![]() $G_0$ and a Borel subgroup
$G_0$ and a Borel subgroup ![]() $B$ of
$B$ of ![]() $G_0$ containing
$G_0$ containing ![]() $T$. Let
$T$. Let ![]() $\Pi =\{\alpha _1,\ldots, \alpha _n\}$ be a set of simple roots with respect to
$\Pi =\{\alpha _1,\ldots, \alpha _n\}$ be a set of simple roots with respect to ![]() $B$ and let
$B$ and let ![]() $\{\omega _1,\ldots,\omega _n\}$ be the respective set of fundamental weights. Enumeration of roots and weight follows Bourbaki.
$\{\omega _1,\ldots,\omega _n\}$ be the respective set of fundamental weights. Enumeration of roots and weight follows Bourbaki.
Denote by ![]() $\Lambda _{\omega }$ the respective weight lattice and by
$\Lambda _{\omega }$ the respective weight lattice and by ![]() $\Lambda _{\omega }^+$ the cone of dominant weights. There is a natural one-to-one correspondence between the isomorphism classes of the irreducible finite-dimensional representations of
$\Lambda _{\omega }^+$ the cone of dominant weights. There is a natural one-to-one correspondence between the isomorphism classes of the irreducible finite-dimensional representations of ![]() $G_0$ and the elements of
$G_0$ and the elements of ![]() $\Lambda _{\omega }^+$. This correspondence associates with an irreducible representation of
$\Lambda _{\omega }^+$. This correspondence associates with an irreducible representation of ![]() $G_0$ its highest weight.
$G_0$ its highest weight.
Now let ![]() $G$ be an arbitrary (not necessarily split) semisimple algebraic group over
$G$ be an arbitrary (not necessarily split) semisimple algebraic group over ![]() $F$ of inner type which is a twisted form of
$F$ of inner type which is a twisted form of ![]() $G_0$. With each element
$G_0$. With each element ![]() $\omega \in \Lambda _{\omega }^+$ one can associate a unique central simple algebra
$\omega \in \Lambda _{\omega }^+$ one can associate a unique central simple algebra ![]() $A_{\omega }$ such that there exists a group homomorphism
$A_{\omega }$ such that there exists a group homomorphism ![]() $\rho : G \rightarrow \operatorname {\mathrm {GL}}_1(A)$ having the property that the representation
$\rho : G \rightarrow \operatorname {\mathrm {GL}}_1(A)$ having the property that the representation ![]() $\rho \otimes F_{\text {sep}}$ of the split group
$\rho \otimes F_{\text {sep}}$ of the split group ![]() $G\otimes F_{\text {sep}}$ is the representation with the highest weight
$G\otimes F_{\text {sep}}$ is the representation with the highest weight ![]() $\omega$. The algebra
$\omega$. The algebra ![]() $A_{\omega }$ is called the Tits algebra of
$A_{\omega }$ is called the Tits algebra of ![]() $G$ corresponding to
$G$ corresponding to ![]() $\omega$. In particular, to any fundamental weight
$\omega$. In particular, to any fundamental weight ![]() $\omega _i$ corresponds a Tits algebra
$\omega _i$ corresponds a Tits algebra ![]() $A_{\omega _i}$.
$A_{\omega _i}$.
Any projective homogeneous ![]() $G$-variety
$G$-variety ![]() $X$ is the variety of parabolic subgroups in
$X$ is the variety of parabolic subgroups in ![]() $G$ of some fixed type, where the type corresponds to a subset
$G$ of some fixed type, where the type corresponds to a subset ![]() $\Theta$ of the set of simple roots
$\Theta$ of the set of simple roots ![]() $\Pi$. The Picard group
$\Pi$. The Picard group ![]() $\mathop {\mathrm {Pic}}(\overline {X})$ can be identified with a free
$\mathop {\mathrm {Pic}}(\overline {X})$ can be identified with a free ![]() $\mathbb {Z}$-module generated by
$\mathbb {Z}$-module generated by ![]() $\omega _i$,
$\omega _i$, ![]() $i \in \Pi \backslash \Theta$. Consider the group homomorphism
$i \in \Pi \backslash \Theta$. Consider the group homomorphism ![]() $\alpha _X: \mathop {\mathrm {Pic}}(\overline {X}) \rightarrow \mathop {\mathrm {Br}}(F)$ sending
$\alpha _X: \mathop {\mathrm {Pic}}(\overline {X}) \rightarrow \mathop {\mathrm {Br}}(F)$ sending ![]() $\omega _i$ to the Brauer class of the Tits algebra
$\omega _i$ to the Brauer class of the Tits algebra ![]() $A_{\omega _i}$ corresponding to the fundamental representation with the highest weight
$A_{\omega _i}$ corresponding to the fundamental representation with the highest weight ![]() $\omega _i$.
$\omega _i$.
By [Reference Merkurjev and TignolMT95, § 2] the following sequence of groups is exact
where ![]() $\mathop {\mathrm {res}}\nolimits$ is the scalar extension to a splitting field of
$\mathop {\mathrm {res}}\nolimits$ is the scalar extension to a splitting field of ![]() $G$.
$G$.
This sequence allows us to express the group ![]() $\mathop {\mathrm {Pic}}(X)$ in terms of the Tits algebras of
$\mathop {\mathrm {Pic}}(X)$ in terms of the Tits algebras of ![]() $G$.
$G$.
3.  $J$-invariant
$J$-invariant
The ![]() $J$-invariant of a semisimple algebraic group was introduced in [Reference Petrov, Semenov and ZainoullinePSZ08] by Petrov, Semenov, and Zainoulline. In this section we briefly recall the definition and the main properties of the
$J$-invariant of a semisimple algebraic group was introduced in [Reference Petrov, Semenov and ZainoullinePSZ08] by Petrov, Semenov, and Zainoulline. In this section we briefly recall the definition and the main properties of the ![]() $J$-invariant following [Reference Petrov, Semenov and ZainoullinePSZ08].
$J$-invariant following [Reference Petrov, Semenov and ZainoullinePSZ08].
Let ![]() $G_0$ be a split semisimple algebraic group over a field
$G_0$ be a split semisimple algebraic group over a field ![]() $F$ and
$F$ and ![]() $B$ a Borel subgroup of
$B$ a Borel subgroup of ![]() $G_0$. An explicit presentation of
$G_0$. An explicit presentation of ![]() $\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$ in terms of generators and relations is known for all groups and all primes
$\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$ in terms of generators and relations is known for all groups and all primes ![]() $p$. Namely, by [Reference KacKac85, Theorem 3]
$p$. Namely, by [Reference KacKac85, Theorem 3]
for some non-negative integers ![]() $r$,
$r$, ![]() $k_i$ and some homogeneous generators
$k_i$ and some homogeneous generators ![]() $e_1,\ldots, e_r$ with degrees
$e_1,\ldots, e_r$ with degrees ![]() $1\leq d_1\leq \cdots \leq d_r$ coprime to
$1\leq d_1\leq \cdots \leq d_r$ coprime to ![]() $p$. A complete list of numbers
$p$. A complete list of numbers ![]() $r$,
$r$, ![]() $k_i$, and
$k_i$, and ![]() $d_i$ is provided in [Reference Petrov, Semenov and ZainoullinePSZ08, p. 21] for any split group
$d_i$ is provided in [Reference Petrov, Semenov and ZainoullinePSZ08, p. 21] for any split group ![]() $G_0$.
$G_0$.
We introduce an order on the set of additive generators of ![]() $\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$, i.e. on the monomials
$\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$, i.e. on the monomials ![]() $e_1^{m_1}\ldots e_r^{m_r}$. To simplify the notation, we denote the monomial
$e_1^{m_1}\ldots e_r^{m_r}$. To simplify the notation, we denote the monomial ![]() $e_1^{m_1}\ldots e_r^{m_r}$ by
$e_1^{m_1}\ldots e_r^{m_r}$ by ![]() $e^M$, where
$e^M$, where ![]() $M$ is an
$M$ is an ![]() $r$-tuple of integers
$r$-tuple of integers ![]() $(m_1, \ldots, m_r)$. The codimension (in the Chow ring) of
$(m_1, \ldots, m_r)$. The codimension (in the Chow ring) of ![]() $e^M$ is denoted by
$e^M$ is denoted by ![]() $|M|$. Note that
$|M|$. Note that ![]() $|M|= \sum _{i=1}^r d_im_i$.
$|M|= \sum _{i=1}^r d_im_i$.
Given two ![]() $r$-tuples
$r$-tuples ![]() $M= (m_1, \ldots, m_r)$ and
$M= (m_1, \ldots, m_r)$ and ![]() $N= (n_1, \ldots, n_r)$ we say
$N= (n_1, \ldots, n_r)$ we say ![]() $e^M \leq e^N$ (or, equivalently,
$e^M \leq e^N$ (or, equivalently, ![]() $M \leq N$) if either
$M \leq N$) if either ![]() $|M|<|N|$ or
$|M|<|N|$ or ![]() $|M|=|N|$ and
$|M|=|N|$ and ![]() $m_i\leq n_i$ for the greatest
$m_i\leq n_i$ for the greatest ![]() $i$ such that
$i$ such that ![]() $m_i \neq n_i$. This gives a well-ordering on the set of all monomials (
$m_i \neq n_i$. This gives a well-ordering on the set of all monomials (![]() $r$-tuples).
$r$-tuples).
Now let ![]() $G = {}_{\xi }G_0$ be an inner twisted form of
$G = {}_{\xi }G_0$ be an inner twisted form of ![]() $G_0$ given by a cocycle
$G_0$ given by a cocycle ![]() $\xi \in Z^1(F, G_0)$ and let
$\xi \in Z^1(F, G_0)$ and let ![]() $X={}_{\xi }(G/B)$ be the variety of Borel subgroups in
$X={}_{\xi }(G/B)$ be the variety of Borel subgroups in ![]() $G$. Since
$G$. Since ![]() $X$ and
$X$ and ![]() $G_0/B$ are isomorphic over any splitting field of
$G_0/B$ are isomorphic over any splitting field of ![]() $G$, we identify the Chow groups
$G$, we identify the Chow groups ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X})$ and
$\mathop {\mathrm {Ch}}\nolimits (\overline {X})$ and ![]() $\mathop {\mathrm {Ch}}\nolimits (G_0/B)$.
$\mathop {\mathrm {Ch}}\nolimits (G_0/B)$.
We consider the following composite map:
where ![]() $\pi$ is the surjective pullback of the canonical projection
$\pi$ is the surjective pullback of the canonical projection ![]() $G_0\to G_0/B$ and
$G_0\to G_0/B$ and ![]() $\mathop {\mathrm {res}}\nolimits$ is the scalar extension to a splitting field of
$\mathop {\mathrm {res}}\nolimits$ is the scalar extension to a splitting field of ![]() $G$.
$G$.
Definition 3.3 [Reference Petrov, Semenov and ZainoullinePSZ08, Definition 4.6]
For each ![]() $i$,
$i$, ![]() $1 \leq i \leq r$, set
$1 \leq i \leq r$, set ![]() $j_i$ to be the smallest non-negative integer such that the image of the composite map
$j_i$ to be the smallest non-negative integer such that the image of the composite map ![]() $\pi \circ \mathop {\mathrm {res}}\nolimits$ contains an element
$\pi \circ \mathop {\mathrm {res}}\nolimits$ contains an element ![]() $a$ with the greatest monomial
$a$ with the greatest monomial ![]() $e_i^{p^{j_i}}$ with respect to the order on
$e_i^{p^{j_i}}$ with respect to the order on ![]() $\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$ as above, i.e., of the form
$\mathop {\mathrm {Ch}}\nolimits ^*(G_0)$ as above, i.e., of the form
 \[ a= e_i^{p^{j_i}} + \sum_{e^M < e_i^{p^{j_i}}} c_M e^M ,\quad c_M \in \mathbb{F}_p . \]
\[ a= e_i^{p^{j_i}} + \sum_{e^M < e_i^{p^{j_i}}} c_M e^M ,\quad c_M \in \mathbb{F}_p . \]
The ![]() $r$-tuple of integers
$r$-tuple of integers ![]() $(j_1, \ldots, j_r)$ is called the
$(j_1, \ldots, j_r)$ is called the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ modulo
$G$ modulo ![]() $p$ and is denoted by
$p$ and is denoted by ![]() $J_p(G)$.
$J_p(G)$.
Remark 3.4 Note that the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ up to a permutation of some components may depend on the choice of the cocycle
$G$ up to a permutation of some components may depend on the choice of the cocycle ![]() $\xi$ (see [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3]). By considering the
$\xi$ (see [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3]). By considering the ![]() $J$-invariant of a group
$J$-invariant of a group ![]() $G$ in the following we also fix a cocycle
$G$ in the following we also fix a cocycle ![]() $\xi$.
$\xi$.
Remark 3.5 According to [Reference Gille and ZainoullineGZ12, Proposition 5.1] and [Reference Karpenko and MerkurjevKM06, Theorem 6.4] the sequence (3.2) of graded rings is exact in the middle term if and only if the cocycle ![]() $\xi$ is generic.
$\xi$ is generic.
In [Reference Petrov, Semenov and ZainoullinePSZ08] the following motivic interpretation of the ![]() $J$-invariant was provided.
$J$-invariant was provided.
Proposition 3.6 [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 5.13]
Let ![]() $X$ be the variety of Borel subgroups in
$X$ be the variety of Borel subgroups in ![]() $G$. Then the Chow motive of
$G$. Then the Chow motive of ![]() $X$ with coefficients in
$X$ with coefficients in ![]() $\mathbb {F}_p$ decomposes into a direct sum
$\mathbb {F}_p$ decomposes into a direct sum
of twisted copies of an indecomposable motive ![]() $\mathcal {R}_p(G)$ for some finite multiset
$\mathcal {R}_p(G)$ for some finite multiset ![]() $I$ of non-negative integers. Moreover, the Poincaré polynomial of
$I$ of non-negative integers. Moreover, the Poincaré polynomial of ![]() $\mathcal {R}_p(G)$ is given by
$\mathcal {R}_p(G)$ is given by
 \begin{equation} P(\mathcal{R}_p(G), t) = \prod_{i=1}^{r} \frac{1-t^{d_ip^{j_i}}}{1-t^{d_i}}. \end{equation}
\begin{equation} P(\mathcal{R}_p(G), t) = \prod_{i=1}^{r} \frac{1-t^{d_ip^{j_i}}}{1-t^{d_i}}. \end{equation}Remark 3.9 Note that the ![]() $J$-invariant allows us to compute not only the Poincaré polynomial of
$J$-invariant allows us to compute not only the Poincaré polynomial of ![]() $\mathcal {R}_p(G)$ by formula (3.8) but also all twisting numbers in the motivic decomposition (3.7) of
$\mathcal {R}_p(G)$ by formula (3.8) but also all twisting numbers in the motivic decomposition (3.7) of ![]() $X\!$. Namely, we have
$X\!$. Namely, we have
 \[ \frac{P(X,t)}{P(\mathcal{R}_p(G), t)} = \sum_{i \geq 0} a_it^i , \]
\[ \frac{P(X,t)}{P(\mathcal{R}_p(G), t)} = \sum_{i \geq 0} a_it^i , \]
where ![]() $a_i$ is the number of the copies of
$a_i$ is the number of the copies of ![]() $\mathcal {R}_p(G)$ with the twisting number
$\mathcal {R}_p(G)$ with the twisting number ![]() $i$ in the motivic decomposition (3.7). Note that the Poincaré polynomial
$i$ in the motivic decomposition (3.7). Note that the Poincaré polynomial ![]() $P(X,t)$ can be explicitly computed by the Solomon formula (see [Reference CarterCar72, 9.4 A]).
$P(X,t)$ can be explicitly computed by the Solomon formula (see [Reference CarterCar72, 9.4 A]).
The motivic decomposition from Proposition 3.6 holds for a more general class of varieties. Namely, a projective homogeneous ![]() $G$-variety
$G$-variety ![]() $X$ is called generically split if the group
$X$ is called generically split if the group ![]() $G$ splits over the generic point of
$G$ splits over the generic point of ![]() $X$. In particular, the variety of Borel subgroups in
$X$. In particular, the variety of Borel subgroups in ![]() $G$ is generically split. Other examples include Pfister quadrics and Severi–Brauer varieties. By [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 5.17] the Chow motive of any generically split
$G$ is generically split. Other examples include Pfister quadrics and Severi–Brauer varieties. By [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 5.17] the Chow motive of any generically split ![]() $G$-variety with coefficients in
$G$-variety with coefficients in ![]() $\mathbb {F}_p$ decomposes into a direct sum of twisted copies of the motive
$\mathbb {F}_p$ decomposes into a direct sum of twisted copies of the motive ![]() $\mathcal {R}_p(G)$.
$\mathcal {R}_p(G)$.
Proposition 3.10 [Reference Petrov and SemenovPS10, Theorem 5.5]
Let ![]() $X$ be a generically split
$X$ be a generically split ![]() $G$-variety and recall that
$G$-variety and recall that ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X)$ denotes the subring of
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X)$ denotes the subring of ![]() $F$-rational cycles in
$F$-rational cycles in ![]() $\mathop {\mathrm {Ch}}\nolimits (X)$. Then
$\mathop {\mathrm {Ch}}\nolimits (X)$. Then
In particular, the number of copies of the motive ![]() $\mathcal {R}_p(G)\{i\}$ in the complete motivic decomposition of
$\mathcal {R}_p(G)\{i\}$ in the complete motivic decomposition of ![]() $X$ is equal to
$X$ is equal to ![]() $\dim _{\, \mathbb {F}_p} \overline {\mathop {\mathrm {Ch}}\nolimits }^i(X)$.
$\dim _{\, \mathbb {F}_p} \overline {\mathop {\mathrm {Ch}}\nolimits }^i(X)$.
Remark 3.11 The above proposition shows that the subring ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X) \subset \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ of
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X) \subset \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ of ![]() $F$-rational cycles encodes the complete motivic decomposition of a generically split variety
$F$-rational cycles encodes the complete motivic decomposition of a generically split variety ![]() $X$ over
$X$ over ![]() $F$. In contrast, in order to find the complete motivic decomposition of a projective homogeneous
$F$. In contrast, in order to find the complete motivic decomposition of a projective homogeneous ![]() $G$-variety
$G$-variety ![]() $X$ in general, one usually needs to describe
$X$ in general, one usually needs to describe ![]() $F$-rational projectors in the Chow group of the product
$F$-rational projectors in the Chow group of the product ![]() $\overline {X \times X}$.
$\overline {X \times X}$.
Remark 3.12 Let ![]() $X$ be a generically split
$X$ be a generically split ![]() $G$-variety. Let
$G$-variety. Let ![]() $\{b_1, \ldots, b_r \}$ and
$\{b_1, \ldots, b_r \}$ and ![]() $\{a_1, \ldots, a_n \}$ be homogeneous bases for
$\{a_1, \ldots, a_n \}$ be homogeneous bases for ![]() $\mathbb {F}_p$-vector spaces
$\mathbb {F}_p$-vector spaces ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X)$ and
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X)$ and ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X})$, respectively. For every
$\mathop {\mathrm {Ch}}\nolimits (\overline {X})$, respectively. For every ![]() $k= 1, \ldots, n$ let
$k= 1, \ldots, n$ let ![]() $\alpha _k \in \mathop {\mathrm {Ch}}\nolimits (X\times X)$ be a preimage of
$\alpha _k \in \mathop {\mathrm {Ch}}\nolimits (X\times X)$ be a preimage of ![]() $a_k$ under the surjective flat pull-back
$a_k$ under the surjective flat pull-back
along the morphism induced by the generic point of the first factor ![]() $X$. Note that
$X$. Note that ![]() $\bar {\alpha }_k = 1 \times a_k + \sum _{i\in I }c_i\times d_i$, where
$\bar {\alpha }_k = 1 \times a_k + \sum _{i\in I }c_i\times d_i$, where ![]() $\operatorname {codim} c_i>0$ for all
$\operatorname {codim} c_i>0$ for all ![]() $i \in I$. Then the set
$i \in I$. Then the set ![]() $\mathcal {B} = \{ (b_i \times 1) \cdot \bar {\alpha }_k \mid i \in [1,r], k \in [1,n] \}$ forms a basis of the
$\mathcal {B} = \{ (b_i \times 1) \cdot \bar {\alpha }_k \mid i \in [1,r], k \in [1,n] \}$ forms a basis of the ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times X)$.
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times X)$.
Indeed, by [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 3.7], the motive ![]() $M(X\times X)$ is isomorphic to a direct sum of twisted copies of the motive
$M(X\times X)$ is isomorphic to a direct sum of twisted copies of the motive ![]() $M(X)$. It follows that
$M(X)$. It follows that
It remains to observe that there are exactly ![]() $rn$ elements in
$rn$ elements in ![]() $\mathcal {B}$ and they are linearly independent.
$\mathcal {B}$ and they are linearly independent.
We finish this section with several observations, which will be useful later in this paper.
Lemma 3.13 Let ![]() $\mathfrak {X}, \mathcal {Y}$ be two projective homogeneous varieties over a field
$\mathfrak {X}, \mathcal {Y}$ be two projective homogeneous varieties over a field ![]() $F$. Assume that
$F$. Assume that ![]() $\mathcal {Y}$ possesses a zero-cycle of degree
$\mathcal {Y}$ possesses a zero-cycle of degree ![]() $1$ over the function field
$1$ over the function field ![]() $F(\mathfrak {X})$. Then the cycle
$F(\mathfrak {X})$. Then the cycle ![]() $a\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X}})$ is
$a\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X}})$ is ![]() $F$-rational if and only if the cycle
$F$-rational if and only if the cycle ![]() $a\times 1\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X} \times \mathcal {Y}} )$ is
$a\times 1\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X} \times \mathcal {Y}} )$ is ![]() $F$-rational.
$F$-rational.
Proof. The direct implication is clear. To show the inverse implication we assume that ![]() $a\times 1\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X} \times \mathcal {Y}} )$ is
$a\times 1\in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathfrak {X} \times \mathcal {Y}} )$ is ![]() $F$-rational.
$F$-rational.
Let ![]() $\alpha \in \mathop {\mathrm {Ch}}\nolimits (\mathfrak {X} \times \mathcal {Y})$ be a cycle, such that
$\alpha \in \mathop {\mathrm {Ch}}\nolimits (\mathfrak {X} \times \mathcal {Y})$ be a cycle, such that ![]() $\overline {\alpha } = a\times 1$. Let
$\overline {\alpha } = a\times 1$. Let ![]() $x \in \mathop {\mathrm {Ch}}\nolimits _0(\mathcal {Y}_{F(\mathfrak {X})})$ be a zero-cycle of degree
$x \in \mathop {\mathrm {Ch}}\nolimits _0(\mathcal {Y}_{F(\mathfrak {X})})$ be a zero-cycle of degree ![]() $1$. Let
$1$. Let ![]() $\beta \in \mathop {\mathrm {CH}}\nolimits (X \times \mathcal {Y})$ be a preimage of
$\beta \in \mathop {\mathrm {CH}}\nolimits (X \times \mathcal {Y})$ be a preimage of ![]() $x$ under the flat pull-back
$x$ under the flat pull-back
along the morphism induced by the generic point of ![]() $\mathfrak {X}$. Since
$\mathfrak {X}$. Since ![]() $\overline {\beta }= 1 \times [\mathbf {pt}] + \sum _{i\in I}a_i\times b_i$, where
$\overline {\beta }= 1 \times [\mathbf {pt}] + \sum _{i\in I}a_i\times b_i$, where ![]() $\dim b_i>0$ for all
$\dim b_i>0$ for all ![]() $i \in I$, we have
$i \in I$, we have
where ![]() $pr_\mathfrak {X}$ is the projection
$pr_\mathfrak {X}$ is the projection ![]() $\mathfrak {X}\times \mathcal {Y} \rightarrow \mathfrak {X}$ on the first factor.
$\mathfrak {X}\times \mathcal {Y} \rightarrow \mathfrak {X}$ on the first factor.
It follows from the above equality that the cycle ![]() $a$ is
$a$ is ![]() $F$-rational.
$F$-rational.
Definition 3.14 Let ![]() $G$ be a semisimple algebraic group of inner type,
$G$ be a semisimple algebraic group of inner type, ![]() $A$ a Tits algebra of
$A$ a Tits algebra of ![]() $G$, and
$G$, and ![]() $X$ a projective homogeneous variety such that
$X$ a projective homogeneous variety such that ![]() $U(X) \simeq R_p(G)$. Let
$U(X) \simeq R_p(G)$. Let ![]() $w \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ be a cycle such that for some lifting
$w \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ be a cycle such that for some lifting ![]() $\tilde {w} \in \mathop {\mathrm {CH}}\nolimits ^1(\overline {X})$ of
$\tilde {w} \in \mathop {\mathrm {CH}}\nolimits ^1(\overline {X})$ of ![]() $w$ holds
$w$ holds ![]() $\alpha _X(\tilde {w})=l [A] \in \mathop {\mathrm {Br}}(F)$, where
$\alpha _X(\tilde {w})=l [A] \in \mathop {\mathrm {Br}}(F)$, where ![]() $l$ is an integer coprime to
$l$ is an integer coprime to ![]() $p$. We define
$p$. We define ![]() $j_{G,A}$ to be the smallest integer
$j_{G,A}$ to be the smallest integer ![]() $j\geq 0$ such that the cycle
$j\geq 0$ such that the cycle ![]() $w^{p^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ is
$w^{p^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ is ![]() $F$-rational.
$F$-rational.
Remark 3.15 Note that the definition of ![]() $j_{G,A}$ does not depend on the choice of the variety
$j_{G,A}$ does not depend on the choice of the variety ![]() $X$ and the cycle
$X$ and the cycle ![]() $w$. Indeed, if
$w$. Indeed, if ![]() $Y$ and
$Y$ and ![]() $v$ is another choice of a variety and a cycle satisfying the above conditions, then using the exact sequence (2.2) for the variety
$v$ is another choice of a variety and a cycle satisfying the above conditions, then using the exact sequence (2.2) for the variety ![]() $X\!\times Y$ we obtain an
$X\!\times Y$ we obtain an ![]() $F$-rational cycle
$F$-rational cycle ![]() $w\times 1 -\lambda (1\times v) \in \mathop {\mathrm {Ch}}\nolimits (\overline {X\!\times Y})$ for some
$w\times 1 -\lambda (1\times v) \in \mathop {\mathrm {Ch}}\nolimits (\overline {X\!\times Y})$ for some ![]() $\lambda \in \mathbb {F}_p^*$. Then for every
$\lambda \in \mathbb {F}_p^*$. Then for every ![]() $j \geq 0$ we have
$j \geq 0$ we have
Hence, we get the following equivalences
where the first and the last equivalences hold by Lemma 3.13.
4. Main result
Let ![]() $F$ be a field and
$F$ be a field and ![]() $p$ a prime number. Let
$p$ a prime number. Let ![]() $G$ be a semisimple algebraic group over a field
$G$ be a semisimple algebraic group over a field ![]() $F$ of inner type. Let
$F$ of inner type. Let ![]() $J(G)=(j_1,\ldots, j_r)$ be the
$J(G)=(j_1,\ldots, j_r)$ be the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ modulo
$G$ modulo ![]() $p$ and let
$p$ and let ![]() $d_1\leq \cdots \leq d_r$ be the respective degrees of the components. Denote by
$d_1\leq \cdots \leq d_r$ be the respective degrees of the components. Denote by ![]() $J^1(G) = (j_1,\ldots,j_l)$,
$J^1(G) = (j_1,\ldots,j_l)$, ![]() $l \leq r$, the family of all components of degree
$l \leq r$, the family of all components of degree ![]() $1$, that is
$1$, that is ![]() $d_l=1$ and
$d_l=1$ and ![]() $d_{l+1}>1$.
$d_{l+1}>1$.
Let ![]() $A$ be a Tits algebra of
$A$ be a Tits algebra of ![]() $G$. Denote by
$G$. Denote by ![]() $F_A$ the function field of the Severi–Brauer variety
$F_A$ the function field of the Severi–Brauer variety ![]() $\mathop {\mathrm {SB}}(A)$. The main theorem of this paper describes the
$\mathop {\mathrm {SB}}(A)$. The main theorem of this paper describes the ![]() $J$-invariant of
$J$-invariant of ![]() $G_{F_A}$ in terms of the
$G_{F_A}$ in terms of the ![]() $J$-invariant of
$J$-invariant of ![]() $G$ over a base field
$G$ over a base field ![]() $F$.
$F$.
Theorem 4.1 Let ![]() $J(G_{F_A})=(j'_1,\ldots, j'_r)$. Then the following hold:
$J(G_{F_A})=(j'_1,\ldots, j'_r)$. Then the following hold:
(i)
 $j_i=j'_i$ for every component of degree
$j_i=j'_i$ for every component of degree  $>1$;
$>1$;(ii)
 $J^1(G) \cup \{0\} = J^1(G_{F_A}) \cup \{j_{G,A}\}$ as multisets;
$J^1(G) \cup \{0\} = J^1(G_{F_A}) \cup \{j_{G,A}\}$ as multisets;(iii) in particular, if
 $J(G) \neq J(G_{F_A})$, then
$J(G) \neq J(G_{F_A})$, then  $j_k \neq j'_k=0$ for some component
$j_k \neq j'_k=0$ for some component  $j_k$ of degree
$j_k$ of degree  $1$.
$1$.
Let ![]() $X$ be a generically split
$X$ be a generically split ![]() $G$-variety and let
$G$-variety and let ![]() $A$ be an algebra which splits over a function field of
$A$ be an algebra which splits over a function field of ![]() $X$ (in particular, this is the case for a Tits algebra of
$X$ (in particular, this is the case for a Tits algebra of ![]() $G$). Before proving the main theorem we need to investigate the relation between
$G$). Before proving the main theorem we need to investigate the relation between ![]() $F$-rational cycles on the variety
$F$-rational cycles on the variety ![]() $\overline {X\times \mathop {\mathrm {SB}}(A)}$ and
$\overline {X\times \mathop {\mathrm {SB}}(A)}$ and ![]() $F_A$-rational cycles on the variety
$F_A$-rational cycles on the variety ![]() $\overline {X}$. Note that
$\overline {X}$. Note that ![]() $\overline {\mathop {\mathrm {SB}}(A)} \simeq \mathbb {P}^{\deg (A) -1}$ and denote by
$\overline {\mathop {\mathrm {SB}}(A)} \simeq \mathbb {P}^{\deg (A) -1}$ and denote by ![]() $h$ the hyperplane class in
$h$ the hyperplane class in ![]() $\mathop {\mathrm {Ch}}\nolimits ^1(\overline {\mathop {\mathrm {SB}}(A)})$.
$\mathop {\mathrm {Ch}}\nolimits ^1(\overline {\mathop {\mathrm {SB}}(A)})$.
Lemma 4.2 Let ![]() $y= a_k \times h^k + \sum _{i>k} a_i\times h^i$ be a homogeneous element in
$y= a_k \times h^k + \sum _{i>k} a_i\times h^i$ be a homogeneous element in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X\times \mathop {\mathrm {SB}}(A)})$, where
$\mathop {\mathrm {Ch}}\nolimits (\overline {X\times \mathop {\mathrm {SB}}(A)})$, where ![]() $a_i \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$. If
$a_i \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$. If ![]() $y$ is rational over
$y$ is rational over ![]() $F$, then:
$F$, then:
(i)
 $1 \times h^k$ is rational over
$1 \times h^k$ is rational over  $F$;
$F$;(ii)
 $a_k$ is rational over
$a_k$ is rational over  $F_A$.
$F_A$.
Proof. We first prove the second statement. We have
where ![]() $i= \deg (A) -1- k$,
$i= \deg (A) -1- k$, ![]() $[pt]$ is the class of a rational point in
$[pt]$ is the class of a rational point in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {\mathop {\mathrm {SB}}(A)})$ and
$\mathop {\mathrm {Ch}}\nolimits (\overline {\mathop {\mathrm {SB}}(A)})$ and ![]() $pr_1: \overline {X\times \mathop {\mathrm {SB}}(A)} \rightarrow \overline {X}$ is the projection on the first factor. Since
$pr_1: \overline {X\times \mathop {\mathrm {SB}}(A)} \rightarrow \overline {X}$ is the projection on the first factor. Since ![]() $y$ and
$y$ and ![]() $1\times h^i$ are both rational over
$1\times h^i$ are both rational over ![]() $F_A$, it follows that
$F_A$, it follows that ![]() $a_k$ is also rational over
$a_k$ is also rational over ![]() $F_A$.
$F_A$.
We now prove the first statement. Consider the surjective pullback
Since ![]() $X$ is split over
$X$ is split over ![]() $F(X \times \mathop {\mathrm {SB}}(A))$, there exists a cycle
$F(X \times \mathop {\mathrm {SB}}(A))$, there exists a cycle ![]() $a_k^*$ in
$a_k^*$ in ![]() $\mathop {\mathrm {Ch}}\nolimits (X_{F(X\times \mathop {\mathrm {SB}}(A))})$, such that
$\mathop {\mathrm {Ch}}\nolimits (X_{F(X\times \mathop {\mathrm {SB}}(A))})$, such that ![]() $\deg (a_k\cdot a_k^*) =1$. Let
$\deg (a_k\cdot a_k^*) =1$. Let ![]() $\alpha$ be the image in
$\alpha$ be the image in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X\times (X\times \mathop {\mathrm {SB}}(A))})$ of some lifting of
$\mathop {\mathrm {Ch}}\nolimits (\overline {X\times (X\times \mathop {\mathrm {SB}}(A))})$ of some lifting of ![]() $a_k^*$ via
$a_k^*$ via ![]() $f$. Let
$f$. Let ![]() $\beta = (pr_{1,3})^*(y)$, where
$\beta = (pr_{1,3})^*(y)$, where ![]() $pr_{1,3}: \overline {X\times X \times \mathop {\mathrm {SB}}(A)} \rightarrow \overline {X\times \mathop {\mathrm {SB}}(A)}$ is the projection on the product of the first and third factors. We have
$pr_{1,3}: \overline {X\times X \times \mathop {\mathrm {SB}}(A)} \rightarrow \overline {X\times \mathop {\mathrm {SB}}(A)}$ is the projection on the product of the first and third factors. We have
and
where ![]() $\operatorname {codim} c_j> 0$ and
$\operatorname {codim} c_j> 0$ and ![]() $\operatorname {codim} b_j < \operatorname {codim} a_k^*$ for all
$\operatorname {codim} b_j < \operatorname {codim} a_k^*$ for all ![]() $j \in I$. Then
$j \in I$. Then
where ![]() $b'_j \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ and
$b'_j \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ and ![]() $\dim b'_j >0$ for all
$\dim b'_j >0$ for all ![]() $j \in I$. Hence,
$j \in I$. Hence, ![]() $(pr_{2,3})_*( \alpha \cdot \beta ) = 1 \times h^k$, where
$(pr_{2,3})_*( \alpha \cdot \beta ) = 1 \times h^k$, where ![]() $pr_{2,3}: \overline {X\times (X\times \mathop {\mathrm {SB}}(A))} \rightarrow \overline {X\times \mathop {\mathrm {SB}}(A)}$ is the projection on the product of second and third factors. Since both cycles
$pr_{2,3}: \overline {X\times (X\times \mathop {\mathrm {SB}}(A))} \rightarrow \overline {X\times \mathop {\mathrm {SB}}(A)}$ is the projection on the product of second and third factors. Since both cycles ![]() $\alpha$ and
$\alpha$ and ![]() $\beta$ are
$\beta$ are ![]() $F$-rational, the cycle
$F$-rational, the cycle ![]() $1 \times h^k$ is also
$1 \times h^k$ is also ![]() $F$-rational.
$F$-rational.
Let ![]() $\mathcal {A}=\{a_1,\ldots, a_s\}$ be a basis of
$\mathcal {A}=\{a_1,\ldots, a_s\}$ be a basis of ![]() $\mathbb {F}_p$-vector subspace of
$\mathbb {F}_p$-vector subspace of ![]() $F_A$-rational cycles in
$F_A$-rational cycles in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X})$. For every
$\mathop {\mathrm {Ch}}\nolimits (\overline {X})$. For every ![]() $i=1,\ldots, s$ we fix an
$i=1,\ldots, s$ we fix an ![]() $F$-rational lifting
$F$-rational lifting ![]() $y_i$ of
$y_i$ of ![]() $a_i$ via the surjective pullback:
$a_i$ via the surjective pullback:
Consider the set
Recall that we denote by ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times \mathop {\mathrm {SB}}(A))$ the subring of
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times \mathop {\mathrm {SB}}(A))$ the subring of ![]() $F$-rational cycles in
$F$-rational cycles in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X\times \mathop {\mathrm {SB}}(A)})$. We can now describe a basis of the
$\mathop {\mathrm {Ch}}\nolimits (\overline {X\times \mathop {\mathrm {SB}}(A)})$. We can now describe a basis of the ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times \mathop {\mathrm {SB}}(A))$ in terms of
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X\times \mathop {\mathrm {SB}}(A))$ in terms of ![]() $\mathcal {A}$ and
$\mathcal {A}$ and ![]() $J$.
$J$.
Proposition 4.4 The set ![]() $\mathcal {B}=\{ y_i \cdot (1\times h^j) \mid i \in [1,s], j \in J\}$ forms a basis of the
$\mathcal {B}=\{ y_i \cdot (1\times h^j) \mid i \in [1,s], j \in J\}$ forms a basis of the ![]() $\mathbb {F}_p$-vector space
$\mathbb {F}_p$-vector space ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(X\!\times \mathop {\mathrm {SB}}(A))$.
$\overline {\mathop {\mathrm {Ch}}\nolimits }(X\!\times \mathop {\mathrm {SB}}(A))$.
Proof. Since ![]() $a_i$,
$a_i$, ![]() $i \in [1,s]$ are linearly independent, the same holds for the elements from
$i \in [1,s]$ are linearly independent, the same holds for the elements from ![]() $\mathcal {B}$. Denote by
$\mathcal {B}$. Denote by ![]() $\langle \mathcal {B} \rangle$ the
$\langle \mathcal {B} \rangle$ the ![]() $\mathbb {F}_p$-vector subspace in
$\mathbb {F}_p$-vector subspace in ![]() ${\mathop {\mathrm {Ch}}\nolimits }(\overline {X\!\times \mathop {\mathrm {SB}}(A)})$ generated by the elements from
${\mathop {\mathrm {Ch}}\nolimits }(\overline {X\!\times \mathop {\mathrm {SB}}(A)})$ generated by the elements from ![]() $\mathcal {B}$. Our goal is to show that
$\mathcal {B}$. Our goal is to show that ![]() $\langle \mathcal {B} \rangle = \overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)})$.
$\langle \mathcal {B} \rangle = \overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)})$.
Clearly ![]() $\langle \mathcal {B} \rangle \subset \overline {\mathop {\mathrm {Ch}}\nolimits }({X\times \mathop {\mathrm {SB}}(A)})$. Assume that the subspaces are not equal and among the homogeneous elements in
$\langle \mathcal {B} \rangle \subset \overline {\mathop {\mathrm {Ch}}\nolimits }({X\times \mathop {\mathrm {SB}}(A)})$. Assume that the subspaces are not equal and among the homogeneous elements in ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }({X\times \mathop {\mathrm {SB}}(A)}) \setminus \langle \mathcal {B} \rangle$ choose an element
$\overline {\mathop {\mathrm {Ch}}\nolimits }({X\times \mathop {\mathrm {SB}}(A)}) \setminus \langle \mathcal {B} \rangle$ choose an element
with the maximal ![]() $k \geq 0$. By Lemma 4.2 the cycle
$k \geq 0$. By Lemma 4.2 the cycle ![]() $a$ is rational over
$a$ is rational over ![]() $F_A$ and
$F_A$ and ![]() $k \in J$. Hence, we can write
$k \in J$. Hence, we can write ![]() $a= \lambda _1 a_1 + \cdots + \lambda _sa_s$ for some
$a= \lambda _1 a_1 + \cdots + \lambda _sa_s$ for some ![]() $\lambda _i \in \mathbb {F}_p$. Consider the cycle
$\lambda _i \in \mathbb {F}_p$. Consider the cycle
By our assumption on ![]() $y$ we see that
$y$ we see that ![]() $y'=0$ and we get a contradiction. It follows that
$y'=0$ and we get a contradiction. It follows that ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)}) = \langle \mathcal {B} \rangle$ and, therefore,
$\overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)}) = \langle \mathcal {B} \rangle$ and, therefore, ![]() $\mathcal {B}$ is indeed a basis of
$\mathcal {B}$ is indeed a basis of ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)})$.
$\overline {\mathop {\mathrm {Ch}}\nolimits }({X\!\times \mathop {\mathrm {SB}}(A)})$.
We are now ready to prove the main theorem.
Proof Proof of Theorem 4.1
Recall that we work with Chow groups and motives modulo ![]() $p$. Without loss of generality we can pass to a field extension of degree coprime to
$p$. Without loss of generality we can pass to a field extension of degree coprime to ![]() $p$ and assume that the index of
$p$ and assume that the index of ![]() $A$ is a power of
$A$ is a power of ![]() $p$. Since in this case the algebra
$p$. Since in this case the algebra ![]() $A$ and its
$A$ and its ![]() $p$-primary component have same splitting fields, we can also assume that the degree
$p$-primary component have same splitting fields, we can also assume that the degree ![]() $n$ of
$n$ of ![]() $A$ is a power of
$A$ is a power of ![]() $p$.
$p$.
Let ![]() $X$ be a generically split
$X$ be a generically split ![]() $G$-variety. Then the variety
$G$-variety. Then the variety ![]() $X\!\times \mathop {\mathrm {SB}}(A)$ is also generically split for the group
$X\!\times \mathop {\mathrm {SB}}(A)$ is also generically split for the group ![]() $G' =G\times \operatorname {\mathrm {PGL}}_1(A)$. Moreover, by Proposition 2.1 and our assumption on algebra
$G' =G\times \operatorname {\mathrm {PGL}}_1(A)$. Moreover, by Proposition 2.1 and our assumption on algebra ![]() $A$, we have
$A$, we have ![]() $\mathcal {R}_p(G) \simeq \mathcal {R}_p(G')$. Applying Proposition 3.10 for the generically split varieties
$\mathcal {R}_p(G) \simeq \mathcal {R}_p(G')$. Applying Proposition 3.10 for the generically split varieties ![]() $X\!\times \mathop {\mathrm {SB}}(A)$ and
$X\!\times \mathop {\mathrm {SB}}(A)$ and ![]() $X_{F_A}$ we obtain
$X_{F_A}$ we obtain
and
Now let us compare the left- and right-hand sides of these polynomial equalities. We have ![]() $P(X\!\times \mathop {\mathrm {SB}}(A), t) = P(X,t) \cdot P(\mathop {\mathrm {SB}}(A), t) =P(X,t) \cdot P(\mathbb {P} ^{n-1}, t) =P(X,t)(({t^n\!-\!1})/({t-1}))$. Note also that
$P(X\!\times \mathop {\mathrm {SB}}(A), t) = P(X,t) \cdot P(\mathop {\mathrm {SB}}(A), t) =P(X,t) \cdot P(\mathbb {P} ^{n-1}, t) =P(X,t)(({t^n\!-\!1})/({t-1}))$. Note also that ![]() $P(X,t) =P(X_{F_A},t)$. The first factor on the right-hand sides of the equalities can be expressed in terms of the corresponding
$P(X,t) =P(X_{F_A},t)$. The first factor on the right-hand sides of the equalities can be expressed in terms of the corresponding ![]() $J$-invariant using formula (3.8). Note that the last factor in the second equality divides the last factor in the first equality by Proposition 4.4 and the quotient is given by the polynomial
$J$-invariant using formula (3.8). Note that the last factor in the second equality divides the last factor in the first equality by Proposition 4.4 and the quotient is given by the polynomial
where the set ![]() $J$ is defined in (4.3).
$J$ is defined in (4.3).
Now dividing the first polynomial equality by the second equality we get
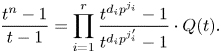 \begin{equation} \frac{t^n-1}{t-1}= \prod_{i=1}^{r} \frac{t^{d_ip^{j_i}}-1}{t^{d_ip^{j'_i}}-1} \cdot Q(t) . \end{equation}
\begin{equation} \frac{t^n-1}{t-1}= \prod_{i=1}^{r} \frac{t^{d_ip^{j_i}}-1}{t^{d_ip^{j'_i}}-1} \cdot Q(t) . \end{equation} The first statement of the theorem follows directly from the above polynomial equality. Indeed, if ![]() $j_i>j'_i$ for some component
$j_i>j'_i$ for some component ![]() $i \in \{1,\ldots,r\}$ with
$i \in \{1,\ldots,r\}$ with ![]() $d_i>1$, then the primitive
$d_i>1$, then the primitive ![]() $d_ip^{j_i}$-root of unity
$d_ip^{j_i}$-root of unity ![]() $\zeta \in \mathbb {C}$ is a complex root of the right-hand-side polynomial from equality (4.5). However,
$\zeta \in \mathbb {C}$ is a complex root of the right-hand-side polynomial from equality (4.5). However, ![]() $\zeta$ is not a complex root of the left-hand-side polynomial in (4.5), since
$\zeta$ is not a complex root of the left-hand-side polynomial in (4.5), since ![]() $n$ is a power of
$n$ is a power of ![]() $p$,
$p$, ![]() $d_i>1$ and
$d_i>1$ and ![]() $p$ does not divide
$p$ does not divide ![]() $d_i$.
$d_i$.
Before proving statements (ii) and (iii) of the theorem we will first find the explicit form of the polynomial ![]() $Q(t)=\sum _{i \in J} t^i$, which is defined by the set
$Q(t)=\sum _{i \in J} t^i$, which is defined by the set ![]() $J$. It follows from polynomial equality (4.5), that
$J$. It follows from polynomial equality (4.5), that ![]() $Q(t)= t^{\deg Q}Q(1/t)$. Hence, the set
$Q(t)= t^{\deg Q}Q(1/t)$. Hence, the set ![]() $J$ is symmetric with respect to its midpoint.
$J$ is symmetric with respect to its midpoint.
Another property
follows from the definition of the set ![]() $J$, since the product of two
$J$, since the product of two ![]() $F$-rational cycles is
$F$-rational cycles is ![]() $F$-rational.
$F$-rational.
Let ![]() $m = \min J\setminus \{0\}$ (we set
$m = \min J\setminus \{0\}$ (we set ![]() $m=n$, if
$m=n$, if ![]() $J=\{0\}$). Using the two above-mentioned properties of the set
$J=\{0\}$). Using the two above-mentioned properties of the set ![]() $J$ it is easy to check that
$J$ it is easy to check that
for some integer ![]() $k \geq 1$, such that
$k \geq 1$, such that ![]() $(k-1)m< n \leq km$.
$(k-1)m< n \leq km$.
Finally, it follows from (4.5), that ![]() $km$ is a power of
$km$ is a power of ![]() $p$ and, thus, is equal to
$p$ and, thus, is equal to ![]() $n$. Moreover,
$n$. Moreover, ![]() $m$ is also a power of
$m$ is also a power of ![]() $p$ and we write
$p$ and we write ![]() $m= p^j$. Therefore, the polynomial
$m= p^j$. Therefore, the polynomial ![]() $Q(t)$ has the following form
$Q(t)$ has the following form ![]() $({t^{n}-1})/({t^{p^j}-1})$.
$({t^{n}-1})/({t^{p^j}-1})$.
Using the description of ![]() $Q(t)$ and the statement (i) of the theorem and formula (4.5) we get
$Q(t)$ and the statement (i) of the theorem and formula (4.5) we get
 \[ (t^{p^j}-1)\prod_{i=1}^{l}{(t^{p^{j'_i}}-1)} = (t-1) \prod_{i=1}^{l}(t^{p^{j_i}}-1) . \]
\[ (t^{p^j}-1)\prod_{i=1}^{l}{(t^{p^{j'_i}}-1)} = (t-1) \prod_{i=1}^{l}(t^{p^{j_i}}-1) . \]
It follows from the above polynomial equality that ![]() $J^1(G_{F_A}) \cup \{j\} = J^1(G) \cup \{0\}$ as multisets. Moreover, by the definition of
$J^1(G_{F_A}) \cup \{j\} = J^1(G) \cup \{0\}$ as multisets. Moreover, by the definition of ![]() $j$ we have
$j$ we have ![]() $j=j_{G,A}$ and we obtain the statement (ii) of the theorem.
$j=j_{G,A}$ and we obtain the statement (ii) of the theorem.
In the case ![]() $J(G_{F_A}) \neq J(G)$, by statement (ii), we have
$J(G_{F_A}) \neq J(G)$, by statement (ii), we have ![]() $j \neq 0$. Hence,
$j \neq 0$. Hence, ![]() $j_k \neq j'_k=0$ for some
$j_k \neq j'_k=0$ for some ![]() $k \in \{1,\ldots,r\}$, which proves the statement (iii) of the theorem.
$k \in \{1,\ldots,r\}$, which proves the statement (iii) of the theorem.
With the same notation as in the above theorem, we get the following corollary.
Corollary 4.6 Assume that there exists a component ![]() $j_i$ of degree one of
$j_i$ of degree one of ![]() $J(G)$, such that all other components of degree one are zero (in particular, this is the case when there is only one component of degree one). Assume also that
$J(G)$, such that all other components of degree one are zero (in particular, this is the case when there is only one component of degree one). Assume also that ![]() $j_i$ becomes zero over
$j_i$ becomes zero over ![]() $F_A$. Then
$F_A$. Then ![]() $j_i = j_{G,A}$.
$j_i = j_{G,A}$.
5.  $J$-invariant of algebras with involutions
$J$-invariant of algebras with involutions
Let ![]() $(A, \sigma )$ be a degree
$(A, \sigma )$ be a degree ![]() $2n$ central simple algebra over
$2n$ central simple algebra over ![]() $F$, endowed with an involution of orthogonal type and trivial discriminant. We refer to [Reference Knus, Merkurjev, Rost and TignolKMRT98] for definitions and classical facts on algebras with involution. Recall, that the Clifford algebra of
$F$, endowed with an involution of orthogonal type and trivial discriminant. We refer to [Reference Knus, Merkurjev, Rost and TignolKMRT98] for definitions and classical facts on algebras with involution. Recall, that the Clifford algebra of ![]() $(A, \sigma )$ splits as a direct product
$(A, \sigma )$ splits as a direct product ![]() $C(A,\sigma )=C_+ \times C_-$ of two central simple algebras over
$C(A,\sigma )=C_+ \times C_-$ of two central simple algebras over ![]() $F$.
$F$.
Let ![]() $G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$ be the connected component of the automorphism group of
$G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$ be the connected component of the automorphism group of ![]() $(A, \sigma )$. Since
$(A, \sigma )$. Since ![]() $(A,\sigma )$ has trivial discriminant, the group
$(A,\sigma )$ has trivial discriminant, the group ![]() $G$ is an inner twisted form of
$G$ is an inner twisted form of ![]() $G_0= \operatorname {\mathrm {PGO}}^+_{2n}$. Both groups
$G_0= \operatorname {\mathrm {PGO}}^+_{2n}$. Both groups ![]() $G$ and
$G$ and ![]() $G_0$ are adjoint of type
$G_0$ are adjoint of type ![]() $\mathrm {D}_{n}$. Let
$\mathrm {D}_{n}$. Let ![]() $\{\omega _1,\ldots,\omega _n\}$ be the respective set of fundamental weights. Note that
$\{\omega _1,\ldots,\omega _n\}$ be the respective set of fundamental weights. Note that ![]() $A$ is a Tits algebra
$A$ is a Tits algebra ![]() $A_{\omega _1}$ of
$A_{\omega _1}$ of ![]() $G$. We fix fundamental weights
$G$. We fix fundamental weights ![]() $\omega _+$ and
$\omega _+$ and ![]() $\omega _-$, which are a permutation of
$\omega _-$, which are a permutation of ![]() $\omega _{n-1}$ and
$\omega _{n-1}$ and ![]() $\omega _n$, in such a way that the Tits algebras
$\omega _n$, in such a way that the Tits algebras ![]() $A_{\omega _+}$ and
$A_{\omega _+}$ and ![]() $A_{\omega _-}$ are the components
$A_{\omega _-}$ are the components ![]() $C_+$ and
$C_+$ and ![]() $C_-$, respectively, of the Clifford algebra
$C_-$, respectively, of the Clifford algebra ![]() $C(A, \sigma )$.
$C(A, \sigma )$.
Note that in this section we assume ![]() $p=2$, which is the only torsion prime of the group
$p=2$, which is the only torsion prime of the group ![]() $G$.
$G$.
Let ![]() $X$ be the variety of Borel subgroups in
$X$ be the variety of Borel subgroups in ![]() $G$. Recall, that the Picard group
$G$. Recall, that the Picard group ![]() $\mathop {\mathrm {Pic}}(\overline {X})$ can be identified with a free
$\mathop {\mathrm {Pic}}(\overline {X})$ can be identified with a free ![]() $\mathbb {Z}$-module generated by
$\mathbb {Z}$-module generated by ![]() $\omega _i$,
$\omega _i$, ![]() $i=1,\ldots,n$. We denote by
$i=1,\ldots,n$. We denote by ![]() $w_i$ the images of
$w_i$ the images of ![]() $\omega _i$ in
$\omega _i$ in ![]() $\mathop {\mathrm {Ch}}\nolimits ^1(\overline {X}) = \mathop {\mathrm {CH}}\nolimits ^1(\overline {X}) \otimes \mathbb {F}_2$.
$\mathop {\mathrm {Ch}}\nolimits ^1(\overline {X}) = \mathop {\mathrm {CH}}\nolimits ^1(\overline {X}) \otimes \mathbb {F}_2$.
In [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12] Quéguiner-Mathieu, Semenov, and Zainoulline introduced the notion of the ![]() $J$-invariant of algebras with orthogonal involutions. The
$J$-invariant of algebras with orthogonal involutions. The ![]() $J$-invariant of
$J$-invariant of ![]() $(A,\sigma )$ is denoted by
$(A,\sigma )$ is denoted by ![]() $J(A, \sigma )$. By definition,
$J(A, \sigma )$. By definition, ![]() $J(A, \sigma )$ is the
$J(A, \sigma )$ is the ![]() $J$-invariant of the respective group
$J$-invariant of the respective group ![]() $G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$, where in the definition of
$G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$, where in the definition of ![]() $J(G)$ we take a cocycle whose class corresponds to
$J(G)$ we take a cocycle whose class corresponds to ![]() $(A, \sigma )$ and a designation of the components
$(A, \sigma )$ and a designation of the components ![]() $C_+$ and
$C_+$ and ![]() $C_-$ (note that the choice of the designation does not affect the value of
$C_-$ (note that the choice of the designation does not affect the value of ![]() $J(G)$; see [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3]).
$J(G)$; see [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3]).
The ![]() $J$-invariant
$J$-invariant ![]() $J(A,\sigma )$ is an
$J(A,\sigma )$ is an ![]() $r$-tuple
$r$-tuple ![]() $(j_1,\ldots,j_r)$, where
$(j_1,\ldots,j_r)$, where ![]() $r=m+1$ if
$r=m+1$ if ![]() $n=2m$ or
$n=2m$ or ![]() $n=2m+1$ (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). Note that the first two components
$n=2m+1$ (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). Note that the first two components ![]() $j_1$ and
$j_1$ and ![]() $j_2$ are of degree
$j_2$ are of degree ![]() $1$ and
$1$ and ![]() $d_i=2i-3$ for
$d_i=2i-3$ for ![]() $i\geq 2$. For every component
$i\geq 2$. For every component ![]() $j_i$ we also have an explicit upper bound
$j_i$ we also have an explicit upper bound ![]() $k_i$ (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). In particular,
$k_i$ (see the table in [Reference Petrov, Semenov and ZainoullinePSZ08, § 4.13]). In particular, ![]() $j_1 \leq k_1 = v_2(n)$, where
$j_1 \leq k_1 = v_2(n)$, where ![]() $v_2(-)$ denotes the
$v_2(-)$ denotes the ![]() $2$-adic valuation. According to [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3] one can take
$2$-adic valuation. According to [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, § 3] one can take ![]() $e_1 = \pi (w_1)$ and
$e_1 = \pi (w_1)$ and ![]() $e_2 = \pi (w_+)$ for the generators in
$e_2 = \pi (w_+)$ for the generators in ![]() $\mathop {\mathrm {Ch}}\nolimits (G_0)$ corresponding to the components
$\mathop {\mathrm {Ch}}\nolimits (G_0)$ corresponding to the components ![]() $j_1$ and
$j_1$ and ![]() $j_2$, respectively, where
$j_2$, respectively, where ![]() $\pi : \mathop {\mathrm {Ch}}\nolimits (\overline {X}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$ is the pullback map (see § 3).
$\pi : \mathop {\mathrm {Ch}}\nolimits (\overline {X}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$ is the pullback map (see § 3).
The goal of this section is to prove Conjecture 1.2 and to explicitly compute ![]() $j_1$.
$j_1$.
By [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] the first component ![]() $j_1$ of
$j_1$ of ![]() $J(A, \sigma )$ is zero if the algebra
$J(A, \sigma )$ is zero if the algebra ![]() $A$ is split. We denote by
$A$ is split. We denote by ![]() $F_A$ the function field of the Severi–Brauer variety of
$F_A$ the function field of the Severi–Brauer variety of ![]() $A$, which is a generic splitting field of
$A$, which is a generic splitting field of ![]() $A$. By Theorem 4.1 we have
$A$. By Theorem 4.1 we have ![]() $J(A, \sigma )_{F_A}= (0, j'_2, j_3,\ldots, j_r)$, that is all components of degree
$J(A, \sigma )_{F_A}= (0, j'_2, j_3,\ldots, j_r)$, that is all components of degree ![]() $> 1$ does not change over
$> 1$ does not change over ![]() $F_A$. However, to prove Conjecture 1.2 we still need to check that
$F_A$. However, to prove Conjecture 1.2 we still need to check that ![]() $j_2=j'_2$. In order to show this we will use the following proposition.
$j_2=j'_2$. In order to show this we will use the following proposition.
Proposition 5.1 The first component ![]() $j_1$ of the
$j_1$ of the ![]() $J(A, \sigma )$ is equal to
$J(A, \sigma )$ is equal to ![]() $j_{G,A}$, where
$j_{G,A}$, where ![]() $G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$.
$G= \operatorname {\mathrm {PGO}}^+(A,\sigma )$.
Proof. Let ![]() $X$ be the variety of Borel subgroups in
$X$ be the variety of Borel subgroups in ![]() $G$. Assume
$G$. Assume ![]() $n$ is odd. By the fundamental relation we have
$n$ is odd. By the fundamental relation we have ![]() $[A] = 2[C_+]=2[C_-] \in \mathop {\mathrm {Br}}(F)$, where
$[A] = 2[C_+]=2[C_-] \in \mathop {\mathrm {Br}}(F)$, where ![]() $C_+$ and
$C_+$ and ![]() $C_-$ are two components of the Clifford algebra of
$C_-$ are two components of the Clifford algebra of ![]() $(A,\sigma )$. Using the exact sequence (2.2) we see that
$(A,\sigma )$. Using the exact sequence (2.2) we see that ![]() $w_1 \in \overline {\mathop {\mathrm {Ch}}\nolimits }(X)$. Hence, by definition,
$w_1 \in \overline {\mathop {\mathrm {Ch}}\nolimits }(X)$. Hence, by definition, ![]() $j_1 =j_{G,A}=0$.
$j_1 =j_{G,A}=0$.
Assume now that ![]() $n$ is even. Observe that in Definition 3.3 of
$n$ is even. Observe that in Definition 3.3 of ![]() $j_1$ we can assume
$j_1$ we can assume ![]() $a = e_1^{2^{j_1}}$. Indeed,
$a = e_1^{2^{j_1}}$. Indeed, ![]() $e_1^{{2}^{j_1}}$ is the smallest monomial of codimension
$e_1^{{2}^{j_1}}$ is the smallest monomial of codimension ![]() ${2}^{j_1}$ with respect to the order defined at the beginning of § 3. Note also that
${2}^{j_1}$ with respect to the order defined at the beginning of § 3. Note also that ![]() $\pi (w_1^{2^{j_1}} ) = e_1^{2^{j_1}}$. It follows from Definition 3.3 that
$\pi (w_1^{2^{j_1}} ) = e_1^{2^{j_1}}$. It follows from Definition 3.3 that ![]() $j_1$ is the smallest non-negative integer, such that there exists an
$j_1$ is the smallest non-negative integer, such that there exists an ![]() $F$-rational homogeneous cycle of the form
$F$-rational homogeneous cycle of the form ![]() $w_1^{2^{j_1}} + \delta \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$, where
$w_1^{2^{j_1}} + \delta \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$, where ![]() $\delta$ is an element of codimension
$\delta$ is an element of codimension ![]() $2^{j_1}$ from the kernel of the map
$2^{j_1}$ from the kernel of the map ![]() $\pi : \mathop {\mathrm {Ch}}\nolimits (\overline {X}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$. Since
$\pi : \mathop {\mathrm {Ch}}\nolimits (\overline {X}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$. Since ![]() $n$ is even, we have
$n$ is even, we have ![]() $[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$. Hence, the cycle
$[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$. Hence, the cycle ![]() $w_1 + w \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ is
$w_1 + w \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ is ![]() $F$-rational, where we set
$F$-rational, where we set ![]() $w= w_+ +w_-$. Therefore, in the definition of
$w= w_+ +w_-$. Therefore, in the definition of ![]() $j_1$ we can replace
$j_1$ we can replace ![]() $w_1$ by
$w_1$ by ![]() $w$.
$w$.
Recall that the kernel of ![]() $\pi$ is the ideal in
$\pi$ is the ideal in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X}) \simeq \mathop {\mathrm {Ch}}\nolimits (G_0/B)$ generated by the rational elements of positive codimension for the twisted form
$\mathop {\mathrm {Ch}}\nolimits (\overline {X}) \simeq \mathop {\mathrm {Ch}}\nolimits (G_0/B)$ generated by the rational elements of positive codimension for the twisted form ![]() $_{\xi }(G_0/B)$ given by a generic cocycle
$_{\xi }(G_0/B)$ given by a generic cocycle ![]() $\xi$ (see Remark 3.5). Our goal is to show that we can assume
$\xi$ (see Remark 3.5). Our goal is to show that we can assume ![]() $\delta = 0$ in the definition of
$\delta = 0$ in the definition of ![]() $j_1$. To do this we first show that, instead of
$j_1$. To do this we first show that, instead of ![]() $X$, we can consider a ‘smaller’ variety, where the cycle
$X$, we can consider a ‘smaller’ variety, where the cycle ![]() $w$ is also defined and where there are ‘few’ rational cycles in the generic case.
$w$ is also defined and where there are ‘few’ rational cycles in the generic case.
Namely, let ![]() $Y$ be the variety of isotropic right ideals in
$Y$ be the variety of isotropic right ideals in ![]() $(A, \sigma )$ of reduced dimension
$(A, \sigma )$ of reduced dimension ![]() $n-1$ (it corresponds to the parabolic subgroup
$n-1$ (it corresponds to the parabolic subgroup ![]() $P \subset G_0$ of type
$P \subset G_0$ of type ![]() $\{1,2,\ldots,n-2\}$). We have a natural projection
$\{1,2,\ldots,n-2\}$). We have a natural projection ![]() $f:X \rightarrow Y$. Since
$f:X \rightarrow Y$. Since ![]() $Y$ is generically split, the projection
$Y$ is generically split, the projection ![]() $f$ is a cellular fibration. Therefore, by [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 3.7] the motive of
$f$ is a cellular fibration. Therefore, by [Reference Petrov, Semenov and ZainoullinePSZ08, Theorem 3.7] the motive of ![]() $X$ decomposes into a direct sum
$X$ decomposes into a direct sum
 \begin{equation} M(X)\simeq \bigoplus_{l=0}^{m} M(Y)\{i_l\} \end{equation}
\begin{equation} M(X)\simeq \bigoplus_{l=0}^{m} M(Y)\{i_l\} \end{equation}
of twisted copies of the motive ![]() $M(Y)$ with some twisting numbers
$M(Y)$ with some twisting numbers ![]() $i_0,\ldots, i_m$, where
$i_0,\ldots, i_m$, where ![]() $i_0 =0$ and
$i_0 =0$ and ![]() $i_l > 0$ for
$i_l > 0$ for ![]() $l \in [1, m]$. More precisely, we have a decomposition of the diagonal class
$l \in [1, m]$. More precisely, we have a decomposition of the diagonal class ![]() $\Delta _X \in \mathop {\mathrm {Ch}}\nolimits (X\!\times X)$ into a sum of pairwise orthogonal projectors
$\Delta _X \in \mathop {\mathrm {Ch}}\nolimits (X\!\times X)$ into a sum of pairwise orthogonal projectors ![]() $\rho _0, \ldots, \rho _m$, such that
$\rho _0, \ldots, \rho _m$, such that ![]() $(X, \rho _l) \simeq M(Y)\{i_l\}$ for every
$(X, \rho _l) \simeq M(Y)\{i_l\}$ for every ![]() $l \in [0,m]$, and, moreover, the Chow group of
$l \in [0,m]$, and, moreover, the Chow group of ![]() $(X, \rho _0) \simeq M(Y)$ as a subgroup of
$(X, \rho _0) \simeq M(Y)$ as a subgroup of ![]() $\mathop {\mathrm {Ch}}\nolimits (X)$ can be identified with
$\mathop {\mathrm {Ch}}\nolimits (X)$ can be identified with ![]() $\mathop {\mathrm {Ch}}\nolimits (Y)$ via the pull-back
$\mathop {\mathrm {Ch}}\nolimits (Y)$ via the pull-back ![]() $f^*$. Thus, we can assume
$f^*$. Thus, we can assume ![]() $\mathop {\mathrm {Ch}}\nolimits (Y) \subset \mathop {\mathrm {Ch}}\nolimits (X)$.
$\mathop {\mathrm {Ch}}\nolimits (Y) \subset \mathop {\mathrm {Ch}}\nolimits (X)$.
Note that decomposition (5.2) also holds for a generic cocycle ![]() $\xi$ (that is, for
$\xi$ (that is, for ![]() ${_{\xi }(G_0/B)}$ and
${_{\xi }(G_0/B)}$ and ![]() ${_{\xi }(G_0/P)}$ instead of
${_{\xi }(G_0/P)}$ instead of ![]() $X$ and
$X$ and ![]() $Y$, respectively). Thus, we can assume that the projectors
$Y$, respectively). Thus, we can assume that the projectors ![]() $\bar {\rho }_0, \ldots, \bar {\rho }_m$ are rational for the generic cocycle. Since
$\bar {\rho }_0, \ldots, \bar {\rho }_m$ are rational for the generic cocycle. Since ![]() $\mathop {\mathrm {Ch}}\nolimits ^0(\overline {X}, \bar {\rho }_l) = 0$ for
$\mathop {\mathrm {Ch}}\nolimits ^0(\overline {X}, \bar {\rho }_l) = 0$ for ![]() $l>0$, the projector
$l>0$, the projector ![]() $\bar {\rho }_l$ can be written, by Remark 3.12, as a linear combination of cycles of the type
$\bar {\rho }_l$ can be written, by Remark 3.12, as a linear combination of cycles of the type ![]() $(b\times 1) \alpha$, where
$(b\times 1) \alpha$, where ![]() $b \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$,
$b \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$, ![]() $\alpha \in \mathop {\mathrm {Ch}}\nolimits (\overline {X\times X})$ are rational in the generic case and
$\alpha \in \mathop {\mathrm {Ch}}\nolimits (\overline {X\times X})$ are rational in the generic case and ![]() $\operatorname {codim} b > 0$. It follows that for
$\operatorname {codim} b > 0$. It follows that for ![]() $l>0$ the Chow group of
$l>0$ the Chow group of ![]() $(\overline {X}, \bar {\rho }_l)$ lies in the kernel of
$(\overline {X}, \bar {\rho }_l)$ lies in the kernel of ![]() $\pi$, that is
$\pi$, that is ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {X}, \bar {\rho }_l) = (\bar {\rho }_l)^*\mathop {\mathrm {Ch}}\nolimits (\overline {X}) \subset \operatorname {Ker} \pi$.
$\mathop {\mathrm {Ch}}\nolimits (\overline {X}, \bar {\rho }_l) = (\bar {\rho }_l)^*\mathop {\mathrm {Ch}}\nolimits (\overline {X}) \subset \operatorname {Ker} \pi$.
Since the cycle ![]() $w$ (and also
$w$ (and also ![]() $w^{2^{j_1}}$) is defined in
$w^{2^{j_1}}$) is defined in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$, the projection of the
$\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$, the projection of the ![]() $F$-rational cycle
$F$-rational cycle ![]() $w^{2^{j_1}} + \delta \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ on the subgroup
$w^{2^{j_1}} + \delta \in \mathop {\mathrm {Ch}}\nolimits (\overline {X})$ on the subgroup ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ is also
$\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ is also ![]() $F$-rational and has the form
$F$-rational and has the form ![]() $w^{2^{j_1}} + \tilde {\delta }$, where
$w^{2^{j_1}} + \tilde {\delta }$, where ![]() $\tilde {\delta } = (\bar {\rho }_0)^*(\delta )$. Note that
$\tilde {\delta } = (\bar {\rho }_0)^*(\delta )$. Note that ![]() $\tilde {\delta } = \delta - \sum _{l=1}^{m} (\bar {\rho }_l)^*(\delta ) \in \operatorname {Ker} \pi$.
$\tilde {\delta } = \delta - \sum _{l=1}^{m} (\bar {\rho }_l)^*(\delta ) \in \operatorname {Ker} \pi$.
Recall that the varieties ![]() $Y$ and
$Y$ and ![]() $G_0/P$ are isomorphic over any splitting field of
$G_0/P$ are isomorphic over any splitting field of ![]() $G$ and consider the pull-back
$G$ and consider the pull-back ![]() $\tilde {\pi }: \mathop {\mathrm {Ch}}\nolimits (\overline {Y}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$ induced by the quotient map. Note that
$\tilde {\pi }: \mathop {\mathrm {Ch}}\nolimits (\overline {Y}) \rightarrow \mathop {\mathrm {Ch}}\nolimits (G_0)$ induced by the quotient map. Note that ![]() $\tilde {\pi } = \pi \circ f^*$. Hence,
$\tilde {\pi } = \pi \circ f^*$. Hence, ![]() $\tilde {\delta } \in \operatorname {Ker} \tilde {\pi }$.
$\tilde {\delta } \in \operatorname {Ker} \tilde {\pi }$.
Denote by ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ the subring of rational cycles in
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ the subring of rational cycles in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {Y}) \simeq \mathop {\mathrm {Ch}}\nolimits (G_0/P)$ for the twisted form
$\mathop {\mathrm {Ch}}\nolimits (\overline {Y}) \simeq \mathop {\mathrm {Ch}}\nolimits (G_0/P)$ for the twisted form ![]() $_{\xi }(G_0/P)$ given by a generic cocycle
$_{\xi }(G_0/P)$ given by a generic cocycle ![]() $\xi$ (note that
$\xi$ (note that ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}} \subseteq \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)$). Let
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}} \subseteq \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)$). Let ![]() $\mathcal {I}$ be the ideal in
$\mathcal {I}$ be the ideal in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ generated by all cycles of positive codimension from
$\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ generated by all cycles of positive codimension from ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$. Note that the parabolic subgroup
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$. Note that the parabolic subgroup ![]() $P \subset G_0$ is special (see [Reference KarpenkoKar18, § 8]) and recall that
$P \subset G_0$ is special (see [Reference KarpenkoKar18, § 8]) and recall that ![]() $\tilde {\delta } \in \operatorname {Ker} \tilde {\pi }$. Applying the exact sequence from [Reference Petrov and SemenovPS17, Lemma 7.1] (for
$\tilde {\delta } \in \operatorname {Ker} \tilde {\pi }$. Applying the exact sequence from [Reference Petrov and SemenovPS17, Lemma 7.1] (for ![]() $G =G_0$,
$G =G_0$, ![]() $S=P$ and a split torsor
$S=P$ and a split torsor ![]() $E$) and using [Reference Karpenko and MerkurjevKM06, Theorem 6.4] we get that
$E$) and using [Reference Karpenko and MerkurjevKM06, Theorem 6.4] we get that ![]() $\tilde {\delta } \in \mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ lies in the ideal
$\tilde {\delta } \in \mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ lies in the ideal ![]() $\mathcal {I}$.
$\mathcal {I}$.
We claim that the minimal non-zero codimension of a cycle in ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ is
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ is ![]() $2^{k_1}$. It would follow from the claim that any non-zero cycle in
$2^{k_1}$. It would follow from the claim that any non-zero cycle in ![]() $\mathcal {I}$ has codimension at least
$\mathcal {I}$ has codimension at least ![]() $2^{k_1}$ and any cycle of codimension
$2^{k_1}$ and any cycle of codimension ![]() $2^{k_1}$ in
$2^{k_1}$ in ![]() $\mathcal {I}$ lies in
$\mathcal {I}$ lies in ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$. In particular, since
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$. In particular, since ![]() $\tilde {\delta }\in \mathcal {I}$ and
$\tilde {\delta }\in \mathcal {I}$ and ![]() $\operatorname {codim} \tilde {\delta }= 2^{j_1} \leq 2^{k_1}$, we obtain that
$\operatorname {codim} \tilde {\delta }= 2^{j_1} \leq 2^{k_1}$, we obtain that ![]() $\tilde {\delta } \in \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ (more precisely,
$\tilde {\delta } \in \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}}$ (more precisely, ![]() $\tilde {\delta } = 0$ if
$\tilde {\delta } = 0$ if ![]() $j_1 < k_1$). Recall that
$j_1 < k_1$). Recall that ![]() $\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}} \subseteq \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)$. Then the cycle
$\overline {\mathop {\mathrm {Ch}}\nolimits }(Y)_{\text {gen}} \subseteq \overline {\mathop {\mathrm {Ch}}\nolimits }(Y)$. Then the cycle ![]() $\tilde {\delta } \in \mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ is also
$\tilde {\delta } \in \mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ is also ![]() $F$-rational and
$F$-rational and ![]() $w^{2^{j_1}} \in \overline {\mathop {\mathrm {Ch}}\nolimits }(X)$. Since
$w^{2^{j_1}} \in \overline {\mathop {\mathrm {Ch}}\nolimits }(X)$. Since ![]() $\alpha _X(\omega _+ + \omega _-)=[A]$, by the definition of
$\alpha _X(\omega _+ + \omega _-)=[A]$, by the definition of ![]() $j_{G,A}$ we have
$j_{G,A}$ we have ![]() $j_{G,A}=j_1$.
$j_{G,A}=j_1$.
It remains to show the above claim. Note that the Poincaré polynomial of ![]() $P(Y,t)$ is known and can be computed by Solomon's formula (see [Reference CarterCar72, 9.4 A]). Using the explicit formula (3.8) for the Poincaré polynomial
$P(Y,t)$ is known and can be computed by Solomon's formula (see [Reference CarterCar72, 9.4 A]). Using the explicit formula (3.8) for the Poincaré polynomial ![]() $P(\mathcal {R}_2({}_\xi G_0), t)$, where
$P(\mathcal {R}_2({}_\xi G_0), t)$, where ![]() $\xi$ is a generic cocycle, and applying Proposition 3.10 we get
$\xi$ is a generic cocycle, and applying Proposition 3.10 we get
It follows that in the generic case a rational cycle in ![]() $\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ has codimension either zero or at least
$\mathop {\mathrm {Ch}}\nolimits (\overline {Y})$ has codimension either zero or at least ![]() $2^{k_1}$. This proves the claim.
$2^{k_1}$. This proves the claim.
Corollary 5.3 Conjecture 1.2 holds.
Proof. The Conjecture follows from Theorem 4.1 and the above proposition.
Let ![]() $J(A,\sigma ) =(j_1 ,j_2, \ldots,j_r)$. Then by the above corollary we have
$J(A,\sigma ) =(j_1 ,j_2, \ldots,j_r)$. Then by the above corollary we have ![]() $J(A, \sigma )_{F_A}= (0,j_2, \ldots, j_r)$. Note that the group
$J(A, \sigma )_{F_A}= (0,j_2, \ldots, j_r)$. Note that the group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$ over the field
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$ over the field ![]() $F_A$ becomes isomorphic to
$F_A$ becomes isomorphic to ![]() $\operatorname {\mathrm {PGO}}^+(q_{\sigma })$, where
$\operatorname {\mathrm {PGO}}^+(q_{\sigma })$, where ![]() $q_{\sigma }$ is the respective quadratic form adjoint to the split algebra with involution
$q_{\sigma }$ is the respective quadratic form adjoint to the split algebra with involution ![]() $(A, \sigma )_{F_A}$. Hence, we can reduce the computation of the components
$(A, \sigma )_{F_A}$. Hence, we can reduce the computation of the components ![]() $j_2, \ldots, j_r$ of
$j_2, \ldots, j_r$ of ![]() $J(A,\sigma )$ to the case of quadratic forms. However, over the field
$J(A,\sigma )$ to the case of quadratic forms. However, over the field ![]() $F_A$ we lose information about the first component
$F_A$ we lose information about the first component ![]() $j_1$. Our next goal is to find an explicit formula for
$j_1$. Our next goal is to find an explicit formula for ![]() $j_1$.
$j_1$.
We know that ![]() $j_1 \leq k_1 = v_2(n)$. Thus,
$j_1 \leq k_1 = v_2(n)$. Thus, ![]() $j_1 =0$ if
$j_1 =0$ if ![]() $n$ is odd. Starting from now, in this section we assume that
$n$ is odd. Starting from now, in this section we assume that ![]() $n$ is a positive even integer.
$n$ is a positive even integer.
Note that in this case all three algebras ![]() $A$,
$A$, ![]() $C_+$, and
$C_+$, and ![]() $C_-$ have exponent
$C_-$ have exponent ![]() $2$. Therefore, the indices of these algebras are powers of
$2$. Therefore, the indices of these algebras are powers of ![]() $2$. We denote by
$2$. We denote by ![]() $i_A$ (respectively, by
$i_A$ (respectively, by ![]() $i_+, i_-$) the
$i_+, i_-$) the ![]() $2$-adic valuation of the index of
$2$-adic valuation of the index of ![]() $A$ (respectively, of
$A$ (respectively, of ![]() $C_+$,
$C_+$, ![]() $C_-$).
$C_-$).
We start the computation of ![]() $j_1$ by collecting upper bounds for
$j_1$ by collecting upper bounds for ![]() $j_1$. Clearly we have
$j_1$. Clearly we have
By [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] we have another upper bound for ![]() $j_1$
$j_1$
Finally, the lemma below shows that
Lemma 5.7 Inequality (5.6) holds.
Proof. Let ![]() $X$ be a variety of Borel subgroups in
$X$ be a variety of Borel subgroups in ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$. Let
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$. Let ![]() $i=\max \{i_+, i_-\}$. Since
$i=\max \{i_+, i_-\}$. Since ![]() $[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$, the cycle
$[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$, the cycle ![]() $w_1 + w_+ +w_- \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ is
$w_1 + w_+ +w_- \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X})$ is ![]() $F$-rational. We have
$F$-rational. We have
By [Reference Petrov and SemenovPS10, Proposition 4.2] the cycles ![]() $w_+^{2^i}$ and
$w_+^{2^i}$ and ![]() $w_-^{2^i}$ are
$w_-^{2^i}$ are ![]() $F$-rational and, hence,
$F$-rational and, hence, ![]() $w_1^{2^i}$ is also
$w_1^{2^i}$ is also ![]() $F$-rational. It follows from the very definition of
$F$-rational. It follows from the very definition of ![]() $j_1$ that
$j_1$ that ![]() $j_1 \leq i$.
$j_1 \leq i$.
Combining upper bounds (5.4), (5.5), and (5.6) we get
It appears that the above upper bound is the exact value of ![]() $j_1$.
$j_1$.
Theorem 5.9 The following formula holds for the first component ![]() $j_1$ of
$j_1$ of ![]() $J(A, \sigma )$:
$J(A, \sigma )$:
Proof. Since inequality (5.8) holds, it remains to show that
Let ![]() $X$ be the variety of totally isotropic ideals in
$X$ be the variety of totally isotropic ideals in ![]() $(A, \sigma )$ of reduced dimension
$(A, \sigma )$ of reduced dimension ![]() $n$ (the variety
$n$ (the variety ![]() $X$ is the twisted form of the variety of maximal totally isotropic subspaces of a quadratic form). Since the discriminant of
$X$ is the twisted form of the variety of maximal totally isotropic subspaces of a quadratic form). Since the discriminant of ![]() $\sigma$ is trivial, the variety
$\sigma$ is trivial, the variety ![]() $X$ has two connected components
$X$ has two connected components ![]() $X^+$ and
$X^+$ and ![]() $X^-$ corresponding to the components
$X^-$ corresponding to the components ![]() $C_+$ and
$C_+$ and ![]() $C_-$, respectively, of the Clifford algebra
$C_-$, respectively, of the Clifford algebra ![]() $C(A, \sigma )$. The varieties
$C(A, \sigma )$. The varieties ![]() $X^+$ and
$X^+$ and ![]() $X^-$ are projective homogeneous under the action of the group
$X^-$ are projective homogeneous under the action of the group ![]() $\operatorname {\mathrm {PGO}}^+(A,\sigma )$.
$\operatorname {\mathrm {PGO}}^+(A,\sigma )$.
Recall that ![]() $\overline {\mathop {\mathrm {SB}}(A)} \simeq \mathbb {P}^{2n -1}$ and denote by
$\overline {\mathop {\mathrm {SB}}(A)} \simeq \mathbb {P}^{2n -1}$ and denote by ![]() $h$ the hyperplane class in
$h$ the hyperplane class in ![]() $\mathop {\mathrm {Ch}}\nolimits ^1(\overline {\mathop {\mathrm {SB}}(A)})$. Note that the variety
$\mathop {\mathrm {Ch}}\nolimits ^1(\overline {\mathop {\mathrm {SB}}(A)})$. Note that the variety ![]() $X= X^+ \times \mathop {\mathrm {SB}}(A)$ and the cycle
$X= X^+ \times \mathop {\mathrm {SB}}(A)$ and the cycle ![]() $1\times h \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X^+ \times \mathop {\mathrm {SB}}(A)})$ satisfy the conditions in Definition 3.14 for the group
$1\times h \in \mathop {\mathrm {Ch}}\nolimits ^1(\overline {X^+ \times \mathop {\mathrm {SB}}(A)})$ satisfy the conditions in Definition 3.14 for the group ![]() $G=\operatorname {\mathrm {PGO}}^+(A,\sigma )$ and central simple algebra
$G=\operatorname {\mathrm {PGO}}^+(A,\sigma )$ and central simple algebra ![]() $A$.
$A$.
Therefore, by Proposition 5.1, ![]() $j_1$ is equal to the smallest integer
$j_1$ is equal to the smallest integer ![]() $j$, such that
$j$, such that ![]() $1 \times h ^{2^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {X^+ \times \mathop {\mathrm {SB}}(A)})$ is
$1 \times h ^{2^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {X^+ \times \mathop {\mathrm {SB}}(A)})$ is ![]() $F$-rational. If
$F$-rational. If ![]() $j$ is such a smallest integer, then
$j$ is such a smallest integer, then ![]() $h ^{2^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathop {\mathrm {SB}}(A)})$ is
$h ^{2^j} \in \mathop {\mathrm {Ch}}\nolimits (\overline {\mathop {\mathrm {SB}}(A)})$ is ![]() $F(X^+)$-rational. It follows that
$F(X^+)$-rational. It follows that ![]() $2^j \geq \mathop {\mathrm {ind}} A_{F(X^+)}$. On the other hand, by the index reduction formula [Reference Merkurjev, Panin and WadsworthMPW96, p. 594] we have
$2^j \geq \mathop {\mathrm {ind}} A_{F(X^+)}$. On the other hand, by the index reduction formula [Reference Merkurjev, Panin and WadsworthMPW96, p. 594] we have
Recall that the algebras ![]() $A$ and
$A$ and ![]() $C_-$ have exponent
$C_-$ have exponent ![]() $2$ and
$2$ and ![]() $[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$. Hence,
$[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$. Hence, ![]() $A\otimes _FA$ is split and the algebras
$A\otimes _FA$ is split and the algebras ![]() $A\otimes _F C_+$ and
$A\otimes _F C_+$ and ![]() $C_-$ are Brauer equivalent. We get
$C_-$ are Brauer equivalent. We get
Therefore, the following inequality holds
Repeating the same arguments but now for the variety ![]() $X^- \times \mathop {\mathrm {SB}}(A)$ we get another inequality
$X^- \times \mathop {\mathrm {SB}}(A)$ we get another inequality
It follows from inequalities (5.11) and (5.12) that ![]() $j_1 \geq \min \{k_1, i_A, \max \{i_+, i_-\}\}$ and we conclude that formula (5.10) holds.
$j_1 \geq \min \{k_1, i_A, \max \{i_+, i_-\}\}$ and we conclude that formula (5.10) holds.
Corollary 5.13 Assume that ![]() $(A,\sigma )$ is half-spin, that is one of the components of the Clifford algebra
$(A,\sigma )$ is half-spin, that is one of the components of the Clifford algebra ![]() $C(A,\sigma )$ is split. Then
$C(A,\sigma )$ is split. Then ![]() $j_1= \min \{k_1, i_A \}$.
$j_1= \min \{k_1, i_A \}$.
Proof. Since ![]() $[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$ and one of the components
$[A]+[C_+]+[C_-]=0 \in \mathop {\mathrm {Br}}(F)$ and one of the components ![]() $C_+$ or
$C_+$ or ![]() $C_-$ is split, we have
$C_-$ is split, we have ![]() $\{i_+, i_-\} = \{i_A, 0 \}$. Then the formula
$\{i_+, i_-\} = \{i_A, 0 \}$. Then the formula ![]() $j_1 = \min \{k_1, i_A \}$ follows from Theorem 5.9.
$j_1 = \min \{k_1, i_A \}$ follows from Theorem 5.9.
The ![]() $J$-invariant of
$J$-invariant of ![]() $(A, \sigma )$ contains two components
$(A, \sigma )$ contains two components ![]() $j_1$ and
$j_1$ and ![]() $j_2$ of degree one. The formula for
$j_2$ of degree one. The formula for ![]() $j_1$ is computed in Theorem 5.9. By [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] we have
$j_1$ is computed in Theorem 5.9. By [Reference Quéguiner-Mathieu, Semenov and ZainoullineQSZ12, Corollary 5.2] we have ![]() $j_2 \leq \min \{i_+, i_-\}$. It appears that this upper bound is the exact value of
$j_2 \leq \min \{i_+, i_-\}$. It appears that this upper bound is the exact value of ![]() $j_2$ in the following case.
$j_2$ in the following case.
Proposition 5.14 If ![]() $\min \{i_+, i_-\} < \min \{k_1, i_A\}$, then
$\min \{i_+, i_-\} < \min \{k_1, i_A\}$, then ![]() $j_2= \min \{i_+, i_-\}$.
$j_2= \min \{i_+, i_-\}$.
Proof. Denote by ![]() $j_i^+$ (respectively,
$j_i^+$ (respectively, ![]() $j_i^-$) the
$j_i^-$) the ![]() $i$th component of the
$i$th component of the ![]() $J$-invariant of
$J$-invariant of ![]() $(A, \sigma )$ over the function field of
$(A, \sigma )$ over the function field of ![]() $\mathop {\mathrm {SB}}(C_+)$ (respectively, of
$\mathop {\mathrm {SB}}(C_+)$ (respectively, of ![]() $\mathop {\mathrm {SB}}(C_-)$). Note that over such a function field the Clifford invariant of
$\mathop {\mathrm {SB}}(C_-)$). Note that over such a function field the Clifford invariant of ![]() $(A, \sigma )$ is trivial. By Corollary 5.13 and using the index reduction formula [Reference Merkurjev, Panin and WadsworthMPW96, p. 592] we have
$(A, \sigma )$ is trivial. By Corollary 5.13 and using the index reduction formula [Reference Merkurjev, Panin and WadsworthMPW96, p. 592] we have
Similarly, we get ![]() $j_1^- = \min \{k_1, i_A, i_+\}$.
$j_1^- = \min \{k_1, i_A, i_+\}$.
Recall that at least one of the numbers ![]() $i_+$ or
$i_+$ or ![]() $i_-$ is less than
$i_-$ is less than ![]() $\min \{k_1, i_A\}$. Hence,
$\min \{k_1, i_A\}$. Hence, ![]() $j_1^+=i_-$ or
$j_1^+=i_-$ or ![]() $j_1^-=i_+$. Let
$j_1^-=i_+$. Let ![]() $\varepsilon$ be a symbol
$\varepsilon$ be a symbol ![]() $+$ or
$+$ or ![]() $-$, such that
$-$, such that ![]() $j_1^{\varepsilon }=\min \{i_+, i_-\}$. Observe that
$j_1^{\varepsilon }=\min \{i_+, i_-\}$. Observe that ![]() $j_2^{\varepsilon }=0$. Therefore, by Theorem 4.1 we have
$j_2^{\varepsilon }=0$. Therefore, by Theorem 4.1 we have ![]() $j_1^{\varepsilon } \in \{j_1,j_2\}$. If
$j_1^{\varepsilon } \in \{j_1,j_2\}$. If ![]() $i_+ \neq i_-$, then by Theorem 5.9 we have
$i_+ \neq i_-$, then by Theorem 5.9 we have
and, hence, ![]() $j_2 = j^{\varepsilon }_1$. Assume now
$j_2 = j^{\varepsilon }_1$. Assume now ![]() $i_+ = i_-$, then
$i_+ = i_-$, then ![]() $j_1 = j^{\varepsilon }_1$. It follows from Theorem 4.1 that
$j_1 = j^{\varepsilon }_1$. It follows from Theorem 4.1 that ![]() $j_2 = j_{G, C_{\varepsilon }}$. Considering the variety
$j_2 = j_{G, C_{\varepsilon }}$. Considering the variety ![]() $X^{-\varepsilon } \times \mathop {\mathrm {SB}}(C_{\varepsilon })$ and applying the index reduction formula in the same way as in the proof of Theorem 5.9 one can check that
$X^{-\varepsilon } \times \mathop {\mathrm {SB}}(C_{\varepsilon })$ and applying the index reduction formula in the same way as in the proof of Theorem 5.9 one can check that ![]() $j_{G, C_{\varepsilon }} \geq i_+ = i_-$. Therefore, in this case we also have
$j_{G, C_{\varepsilon }} \geq i_+ = i_-$. Therefore, in this case we also have ![]() $j_2 = \min \{i_+, i_-\}$.
$j_2 = \min \{i_+, i_-\}$.
Acknowledgements
I am grateful to Anne Quéguiner-Mathieu for introducing me to Conjecture 1.2 and for useful discussions. I would like to thank Nikita Semenov for numerous useful discussions on the subject of this paper.
Conflicts of interest
None.
Financial support
The author gratefully acknowledges the support of the DFG project ZH 918/2-1.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.