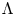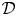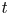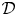Irregular perverse sheaves

Abstract

We introduce irregular constructible sheaves, which are ${\mathbb {C}}$-constructible with coefficients in a finite version of the Novikov ring $\Lambda$ and special gradings. We show that the bounded derived category of cohomologically irregular constructible complexes is equivalent to the bounded derived category of holonomic ${\mathcal {D}}$-modules by a modification of D’Agnolo and Kashiwara's irregular Riemann–Hilbert correspondence. The bounded derived category of cohomologically irregular constructible complexes is equipped with the irregular perverse $t$-structure, which is a straightforward generalization of usual perverse $t$-structure, and we prove that its heart is equivalent to the abelian category of holonomic ${\mathcal {D}}$-modules. We also develop the algebraic version of the theory.

1. Introduction

The regular Riemann–Hilbert correspondence (formulated and proved by Kashiwara [Kas84], and another proof given by Mebkhout [Meb84]) states that the derived category of regular holonomic ${\mathcal {D}}$-modules is equivalent to the derived category of ${\mathbb {C}}$-constructible sheaves. Under this equivalence, the abelian category of regular holonomic ${\mathcal {D}}$-modules is mapped to the abelian category of perverse sheaves introduced by Beilinson, Bernstein, Deligne and Gabber [Kas75, BBD82, GM80].

After many efforts including understanding of formal and asymptotic structures [Maj84, Sab00, Moc11, Ked11], Stokes phenomena and Riemann–Hilbert correspondence for meromorphic connections [Mal83, Sib90, DMR07, Moc11, Sab13], sophistication of the regular Riemann–Hilbert correspondence [KS01], and developments of ind-sheaves and the discovery of its relation to asymptotic behavior [KS01, KS03], in a seminal paper [DK16], D’Agnolo and Kashiwara formulated and proved the irregular Riemann–Hilbert correspondence for holonomic ${\mathcal {D}}$-modules.

Theorem 1.1 (D'Agnolo and Kashiwara [DK16])

For a complex manifold $X$, there exists a fully faithful embedding

(1.1)\begin{equation} D^b_{\mathrm{hol}}({\mathcal{D}}_X)\hookrightarrow E^b_{{\mathbb{R}} - c}(\mathrm{I}{\mathbb {C}}_X), \end{equation}

where the left-hand side is the derived category of cohomologically holonomic ${\mathcal {D}}$-modules and the right-hand side is the category of $\,\mathbb{R}$-constructible ${\mathbb {C}}$-valued enhanced ind-sheaves. There also exists an explicit construction of a right quasi-inverse of the above embedding.

In the sequel [DK19], they also introduced the notion of enhanced perverse $t$-structure on the right-hand side of the embedding and proved that the embedding is $t$-exact in a slightly generalized sense. Moreover, Mochizuki [Moc16] proved that the image of the equivalence can be characterized by testing on curves.

In this paper, we modify the right-hand side of the equivalence and make it closer to the form of the regular Riemann–Hilbert correspondence.

As mentioned in their paper, D’Agnolo and Kashiwara's clever definition and use of enhanced sheaves are inspired from the construction of Tamarkin [Tam18]. Tamarkin's idea of adding one extra variable originally aimed to realize the Novikov ring action in sheaf theory as in Fukaya category [FOOO09]. In this paper, we take a way which is closer to this original idea instead of the use of enhanced sheaves. The replacement for the right-hand side of (1.1) is expressed as graded modules (sheaves) over the ‘finite Novikov ring’ $\Lambda :=\mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ where $\mathbb {k}\subset {\mathbb {C}}$ is a field. An element of $\Lambda$ is expressed as a finite sum $\sum _{a\in {\mathbb {R}}_{\geqslant 0}}c_aT^a$ where $T$ is the indeterminate. A priori, the hom-spaces $\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})$ of $\Lambda$-modules are defined over $\Lambda$. By taking the tensor product $\operatorname {Hom}( {\mathcal {V}}, {\mathcal {W}})\otimes _{\Lambda }\mathbb {k}$ where $\Lambda \rightarrow \mathbb {k}$ is defined by $T^a\mapsto 1$, we obtain a new category $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. We will further modify this category to obtain $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We can consider $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ as an approximate description of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.

The category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian and has enough injective and flat objects. We define an abelian subcategory of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$: the category of irregular constructible sheaves $\mathrm {Mod}_{ic}(\Lambda _X)$. Then we set $D^b_{ic}(\Lambda _X)$ as the full subcategory of the bounded derived category $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ consisting of cohomologically irregular constructible sheaves. The meaning of irregular constructibility is as follows. As usual, there exists a ${\mathbb {C}}$-Whitney stratification and we have a sheaf which is locally constant as $\Lambda$-module over each stratum, but moreover with particular gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem [Sab00, Moc11, Ked11]. Then we have the following.

Theorem 1.2

1. (i) The category $D^b_{ic}(\Lambda _X)$ has functors $\mathop {{{\mathcal {H}}}om}\nolimits , \otimes , f^{-1}, f^!$ for any morphism $f$ and $f_!$ for proper $f$.

2. (ii) If $\,\mathbb{k}={\mathbb {C}}$, there exists an equivalence

   (1.2)\begin{equation} D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq} D^b_{ic}(\Lambda_X). \end{equation}

In our formulation, the data of exponential factors of solutions of irregular differential equations are encoded in the grading of $\Lambda$-modules. We would like to apply the following trivial fact to our setting. For a graded ring $R$, the grading-forgetful functor from the abelian category of graded $R$-modules to the abelian category of $R$-modules is exact. Although our category $\mathrm {Mod}_{ic}(\Lambda _X)$ has a modification of hom-spaces, we still have the following.

Theorem 1.3 There exists an exact functor $ {\mathfrak {F}}$ from $\mathrm {Mod}_{ic}(\Lambda _X)$ to the abelian category of ${\mathbb {C}}$-constructible sheaves $\mathrm {Mod}_{c}(\mathbb {k}_X)$ such that, on the level of stalks, this is the composition of the grading-forgetful map and tensoring $\mathbb {k}$ over $\Lambda$.

By using $ {\mathfrak {F}}$, we can define the support of an irregular constructible sheaf $ {\mathcal {V}}$ by $\mathrm {supp}\, {\mathcal {V}}:=\mathrm {supp}\, {\mathfrak {F}}( {\mathcal {V}})$. By using this definition, we can define the irregular perverse $t$-structure by the same formula as in usual perverse sheaves. Let ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of $D^b_{ic}(\Lambda _X)$ spanned by objects satisfying

(1.3)\begin{equation} \dim\{\mathrm{supp}\, H^j({\mathcal{V}})\}\leqslant -j \hspace{3mm} (\text{respectively }\dim\{\mathrm{supp}\, H^j({\mathbb{D}}{\mathcal{V}})\}\leqslant -j ) \text{ for any }j\in {\mathbb{Z}}. \end{equation}

Theorem 1.4

1. (i) The pair $({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ defines a $t$-structure of $D^b_{ic}(\Lambda _X)$, which we call irregular perverse $t$-structure.

2. (ii) The heart of irregular perverse $t$-structure $\mathrm {Perv}_{ic}({\mathbb {C}}_X)$ over ${\mathbb {C}}$ is equivalent to the abelian category of holonomic ${\mathcal {D}}$-modules under the equivalence (1.2).

We also prove the corresponding results in the algebraic setting. Mostly, the statements are corollaries of analytic cases, although we also have $f_*$ and $f_!$ for any morphism and can prove stronger commutativity results for the Riemann–Hilbert functor (as in the case of algebraic regular Riemann–Hilbert correspondence).

In the rest of this section, we would like to shortly discuss a conjectural explanation of the appearance of the Novikov ring. Recall that Tamarkin's introduction of additional $ {\mathbb {R}}$ was motivated by Floer theory/Fukaya category. Fukaya category is naturally enriched with the Novikov ring by estimating disk areas (Gromov's compactness theorem for holomorphic disks). We expect this appearance of the Novikov ring and the one in our construction can be identified as follows.

We denote the derived category of regular holonomic ${\mathcal {D}}$-modules by $D^b_{\mathrm {reghol}}({\mathcal {D}}_X)$. Combining the regular Riemann–Hilbert correspondence with the Nadler–Zaslow equivalence [NZ09], we have an embedding $D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b\operatorname {\mathfrak {Fuk}}^{NZ}(T^*X)$, where the right-hand side is Nadler and Zaslow's Fukaya category of conic Lagrangians in $T^*X$.

We expect a similar claim for the holonomic case: there exists a Fukaya category $D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)$ enriched over $\Lambda$ of $T^*X$ with nonconic Lagrangians which has a fully faithful embedding from the category $D^b_{{ic},\Lambda }(\Lambda _X)$ which is a version of $D^b_{ic}(\Lambda _X)$ enriched over $\Lambda$. After the reduction of coefficient from $\Lambda$ to $\mathbb {k}$, we will obtain an embedding of $D^b_{ic}(\Lambda _X)$ into a version of Fukaya category. On the level of objects, the exponential ${\mathcal {D}}_X$-module associated to a meromorphic function $f$ will correspond to the Lagrangian $\mathrm {Graph}(df)$.

If this expectation is true, one can imagine $K$-theory classes of objects of $D\operatorname {\mathfrak {Fuk}}_{ic}(T^*X):=D\operatorname {\mathfrak {Fuk}}_{ic}^\Lambda (T^*X)\otimes _\Lambda \mathbb {k}$ as an irregular version of characteristic cycle. In the same vein, their supports can be considered as an irregular version of microsupports, which are no longer conic. Hence one can also imagine a generalization of microlocal analysis. Note that a version (real blown-up version) of the equivalence without $\Lambda$ is already appeared if one fixes a formal type [STWZ15]. Also, another connection between Riemann–Hilbert correspondence and holomorphic Fukaya category is conjectured by Kontsevich [Kon16], whose relation to our conjecture is also of interest.

The organization of this paper is as follows. In § 2, we define and discuss the preliminary version of the category of sheaves with coefficients in $\Lambda$. In §§ 3 and 4, we define the (derived) category of sheaves with coefficients in $\Lambda$ over topological spaces with boundary and consider various (derived) functorial operations as in usual sheaf theory. In § 5, we define our main objects irregular constructible sheaves and again see various functorial operations. We also note that irregular constructible sheaves are actually sheaves. In § 6, we construct the functor $ {\mathfrak {F}}$ which relates irregular to usual sheaves. In § 7, we see the relationship between enhanced sheaves and our $\Lambda$-modules, which enables us to establish our version of Riemann–Hilbert correspondence using D’Agnolo and Kashiwara's theorem in § 8. We also prove some commutativity results for Riemann–Hilbert functor in § 8. In § 9, we define irregular perverse sheaves by using $ {\mathfrak {F}}$ and import results in the theory of perverse sheaves to irregular perverse sheaves. In § 10, we discuss algebraic version of the above story.

2. $\Lambda _X$-modules

In this section, we introduce the ‘finite Novikov ring’ $\Lambda$ and its modules. We fix a field $\mathbb {k}\subset {\mathbb {C}}$ once and for all.

2.1 The ring $\Lambda$

Let us consider the set of nonnegative real numbers $\mathbb{R} _{\geqslant 0}$ as a semigroup by the addition. We denote the associated polynomial ring by $\Lambda :=\Lambda _\mathbb {k}:=\mathbb {k}[\mathbb{R} _{\geqslant 0}]$. For $a\in \mathbb{R} _{\geqslant 0}$, let us denote the corresponding indeterminate by $T^a$. We set $\operatorname {Gr}^a\Lambda :=\mathbb {k}\cdot T^a\subset \Lambda$ for $a\geqslant 0$, which gives an $ {\mathbb {R}}$-grading on $\Lambda$.

Let $\mathrm {Mod}^0(\Lambda )$ be the abelian category of $ {\mathbb {R}}$-graded $\Lambda$-modules with degree $0$ morphisms. For an $ {\mathbb {R}}$-graded $\Lambda$-module $V$, let $V\langle a\rangle$ be the grading shift of $M$ i.e. $\operatorname {Gr}^bV\langle a\rangle :=\operatorname {Gr}^{a+b} V$. We set

(2.1)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathbb{R}}(\Lambda)}(V,W):=\bigoplus_{a\in {\mathbb{R}}}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda)}(V, W\langle a\rangle) \end{equation}

for $ {\mathbb {R}}$-graded $\Lambda$-modules. The category $\mathrm {Mod}^ {\mathbb {R}}(\Lambda )$ is consisting of $ {\mathbb {R}}$-graded modules with the hom-spaces defined by (2.1). We set

(2.2)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathbb{R}}(\Lambda)}^a(V,W):=\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda)}(V, W\langle a\rangle). \end{equation}

2.2 $\Lambda _X$-modules

Let $X$ be a complex manifold. Let $\Lambda _X$ be the constant sheaf valued in $\Lambda$.

Definition 2.1 A sheaf of $ {\mathbb {R}}$-graded $\Lambda _X$-module is a sheaf valued in $\mathrm {Mod}^0(\Lambda )$.

Let $\tilde {\mathcal{V} }$ be a sheaf of $ {\mathbb {R}}$-graded $\Lambda _X$-modules. For an open subset $U\subset X$, we have an $ {\mathbb {R}}$-graded $\Lambda$-module $\tilde {\mathcal{V} }(U)$. For an inclusion $U\hookrightarrow V$, we have a map $\tilde {\mathcal{V} }(V)\rightarrow \tilde {\mathcal{V} }(U)$ which respects the grading $\operatorname {Gr}^a\tilde {\mathcal{V} }(V)\rightarrow \operatorname {Gr}^a\tilde {\mathcal{V} }(U)$. Hence we have a sheaf of $\mathbb {k}$-vector spaces $\operatorname {Gr}^a\tilde {\mathcal{V} }$ and an isomorphism $\tilde {\mathcal{V} }\cong {\bigoplus} _{a}\operatorname {Gr}^a\tilde {\mathcal{V} }$ as sheaves valued in $\mathbb {k}$-vector spaces.

We denote the category of $ {\mathbb {R}}$-graded $\Lambda _X$-modules by $\mathrm {Mod}^0(\Lambda _X)$.

Proposition 2.2 The category $\mathrm {Mod}^0(\Lambda _X)$ is abelian.

Proof. This is because $\mathrm {Mod}^0(\Lambda )$ is abelian.

Notation 2.1 $\tilde {\mathcal{V} }\langle a\rangle$ for $a\in {\mathbb {R}}$ is $a$-shift of $\tilde {\mathcal{V} }$ as in the previous subsection. For $f\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }$, $f\langle a\rangle$ means the shifted morphism $\tilde {\mathcal{V} }\langle a\rangle \rightarrow \tilde {\mathcal{W} }\langle a\rangle$.

We set

(2.3)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{V}},\tilde{\mathcal{W}}):=\bigoplus_{a\in {\mathbb{R}}}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_X)}(\tilde{\mathcal{V}}, \tilde{\mathcal{W}}\langle a\rangle) \end{equation}

and

(2.4)\begin{equation} \operatorname{Hom}^a_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{V}},\tilde{\mathcal{W}}):=\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_X)}(\tilde{\mathcal{V}}, \tilde{\mathcal{W}}\langle a\rangle). \end{equation}

Note that $\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ is a $\Lambda$-module. We see $\mathbb {k}$ as a $\Lambda$-module by setting $f\cdot c:=f|_{T=1}c$ for $f\in \Lambda$ and $c\in \mathbb {k}$. We set

(2.5)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{pre}(\Lambda_X)}([\tilde{\mathcal{V}}], [\tilde{\mathcal{W}}]):=\operatorname{Hom}_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{V}}, \tilde{\mathcal{W}})\otimes_\Lambda \mathbb{k}. \end{equation}

Definition 2.3 The category $\mathrm {Mod}_{pre}^ {\mathfrak {I}}(\Lambda _X)$ is defined by the following data. The set of objects is the set of $ {\mathbb {R}}$-graded $\Lambda _X$-modules. For an $ {\mathbb {R}}$-graded $\Lambda _X$-module $\tilde {\mathcal{V} }$, the corresponding object in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is denoted by $[\tilde {\mathcal{V} }]$.

The hom-space between $[\tilde {\mathcal{V} }]$ and $[\tilde {\mathcal{W} }]$ is $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{V} }], [\tilde {\mathcal{W} }])$ defined in the above.

There is a canonical functor $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which is the identity on objects and takes a morphism $f$ to $f\otimes 1$.

Remark 2.4 Here we would like to explain some motivations of Definition 2.3. We would like to consider usual sheaves endowed with a filtration indexed by $ {\mathbb {R}}$. A typical example is a sheaf $\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\geqslant -a}$ ($a\in {\mathbb {R}}$) where $\phi$ is a continuous function on $X{\backslash } D$ where $D$ is a divisor of $X$. A typical $\phi$ is a meromorphic function with poles in $D$ only determined up to adding a holomorphic function. This leads to considering $ {\mathbb {R}}$-filtrations up to a shift. Making the category of $ {\mathbb {R}}$-filtered vector spaces abelian is realized by the Rees trick which gives us $\Lambda$-modules. Flat modules are $ {\mathbb {R}}$-filtered vector spaces. Instead of ignoring shifts of gradings, we modify the notion of morphisms: the multiplication by $T^a\in \mathbb {k}[ {\mathbb {R}}_{\geqslant 0}]$ becomes the identity to identify an object with its $a$-shift.

Definition 2.5 For an object $ {\mathcal {V}}$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, a lift is a pair of an object $\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$ and an isomorphism $[\tilde {\mathcal{V} }]\xrightarrow {\cong } {\mathcal {V}}$. In the following, we usually do not write this isomorphism explicitly for simplicity.

Proposition 2.6 The category $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian category.

To prove this proposition, we prepare some lemmas.

Lemma 2.7 Let $V$ be an $ {\mathbb {R}}$-graded $\Lambda$-module. Let $s$ be a homogeneous element of $V$. If $T^a\cdot s \neq 0$ for any $a\in {\mathbb {R}}\geqslant 0$, then $s\otimes 1$ is nonzero in $V\otimes _\Lambda \mathbb {k}$.

Proof. Note that $l\cdot s$ is nonzero for any $l\in \Lambda {\backslash }\{0\}$. We have an inclusion $\Lambda \cdot s\hookrightarrow V$. Since the left-hand side is a free $\Lambda$-module, the tensoring $(-)\otimes _\Lambda \mathbb {k}$ preserves the inclusion. Hence $s\otimes 1$ is nonzero in $V\otimes _\Lambda \mathbb {k}$.

From Lemma 2.8 to Lemma 2.12, we will use the following notation: $ {\mathcal {V}}=[\tilde { {\mathcal {V}}}], {\mathcal {W}}=[\tilde {{\mathcal {W}}}]$.

Lemma 2.8 For $f\in \operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$, if $T^af\neq 0$ for any $a\in \mathbb{R} _{\geqslant 0}$, then $f$ is nonzero as an element in $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$.

Proof. This is a case of Lemma 2.7 by setting $V=\operatorname {Hom}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ and $s:=f$.

Lemma 2.9 For $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists $b\in {\mathbb {R}}$ such that there exists

(2.6)\begin{equation} f'\in\operatorname{Hom}^b_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{V}},\tilde{\mathcal{W}}) \end{equation}

which is a lift of $f$.

Proof. Take a lift $f={\bigoplus} _{c}f_c\in {\bigoplus} _{c}\operatorname {Hom}^c_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$. Since $f_c$ is zero except for finite $c$, we can take $b$ to be a real number which is greater than or equal to the maximum of $c$ for which $f_c$ is nonzero. Then we set

(2.7)\begin{equation} f':=\bigoplus_{c}T^{b-c}f_c\in \operatorname{Hom}^b_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{V}},\tilde{\mathcal{W}}). \end{equation}

Since $T^{b-c}=1$ on $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, the element $f'$ represents $f$.

Lemma 2.10 Let $f_i\in \operatorname {Hom}^{b_i}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$ $(i=1,2)$ be lifts of $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$. Then there exists $b_i\in \mathbb{R} _{\geqslant 0}$ such that $T^{b_1}f_1=T^{b_2}f_2$.

Proof. By multiplying some $T^a$ values we can assume that $b_1=b_2$. Since $f_1-f_2$ represents $0$ in $\operatorname {Hom}_{\mathrm {Mod}_{pre}^{ {\mathfrak {I}}}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, there exists $b\in \mathbb{R} _{\geqslant 0}$ such that $T^b(f_1-f_2)=0$ by Lemma 2.8.

Lemma 2.11 For $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}},{\mathcal {W}})$, let $f'\in \operatorname {Hom}^{b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{V} },\tilde {\mathcal{W} })$ be a lift. We view $f'$ as a degree $0$ morphism between $\tilde {\mathcal{V} }$ and $\tilde {\mathcal{W} }\langle b\rangle$ in $\mathrm {Mod}^0(\Lambda _X)$. The objects $[\ker (f')]$, $[\mathrm {im}(f')]$, $[\operatorname {coker}(f')]$, and $[\mathrm {coim}(f')]$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ only depend on $f$.

Proof. By Lemma 2.10, it suffices to prove the objects defined for $f'$ and $T^af'$ are isomorphic. We have morphisms $f'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle b\rangle$ and $T^af'\colon \tilde {\mathcal{V} }\rightarrow \tilde {\mathcal{W} }\langle a+b\rangle$ in $\mathrm {Mod}^0(\Lambda _X)$. Note that $\ker f'\hookrightarrow \ker T^af'$. Hence for any $\tilde {\mathcal{P} }\in \mathrm {Mod}^0(\Lambda _X)$, we have

(2.8)\begin{equation} \tilde{c}\colon \bigoplus_{b\in {\mathbb{R}}}\operatorname{Hom}^b_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{P}}, \ker f')\hookrightarrow\bigoplus_{b\in {\mathbb{R}}}\operatorname{Hom}^b_{\mathrm{Mod}^{\mathbb{R}}(\Lambda_X)}(\tilde{\mathcal{P}}, \ker T^af'), \end{equation}

which induces a comparison morphism

\[ c\colon \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }], [\ker f'])\rightarrow \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }], [\ker T^af']) \]

It suffices to show that $c$ is an isomorphism.

For any $g\in \operatorname {Hom}^b_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$, consider $T^ag\in \operatorname {Hom}^{a+b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker T^af')$. Since $f'\langle a+b\rangle \circ T^a g=T^af'\langle b\rangle \circ g=0$, $T^ag$ factors through $\ker f'\langle a+b\rangle$ i.e.

\[ T^ag\in \operatorname {Hom}^{a+b}_{\mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)}(\tilde {\mathcal{P} }, \ker f'). \]

Hence $T^ag$ is in the image of $\tilde {c}$. Since $g$ and $T^ag$ represents the same morphism in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, we have the surjectivity of $c$.

On the other hand, let $g\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }],[\ker f'])$ be zero in $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([\tilde {\mathcal{P} }], [\ker T^af'])$. For a lift $g'$ of $g$, we have $T^bg'=0$ for some $b\in \mathbb{R} _{\geqslant 0}$ by Lemma 2.8. Hence $g=0\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)}([P], [\ker f'])$. This gives the injectivity of $c$.

Similar arguments prove the claims for $\mathrm {im}(f')$, $\operatorname {coker}(f')$, and $\mathrm {coim}(f')$.

Lemma 2.12 The objects defined in Lemma 2.11 actually give kernel, image, cokernel, and coimage in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$.

Proof. Again, we will only prove for kernel and the others can be proved by similar arguments.

Let ${\mathcal {P}}\xrightarrow {g} {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ satisfy $f\circ g=0$. We have lifts

(2.9)\begin{equation} \tilde{\mathcal{P}}\xrightarrow{\tilde{g}}\tilde{\mathcal{V}}\xrightarrow{\tilde{f}}\tilde{\mathcal{W}} \end{equation}

in $\mathrm {Mod}^0(\Lambda _X)$. By replacing $\tilde {\mathcal{W} }$ with $\tilde {\mathcal{W} }\langle c\rangle$ with sufficiently large $c$ and $\tilde {f}$ with $T^c\tilde {f}$, we can take so that $\tilde {f}\circ \tilde {g}=0$ by Lemma 2.8. Then there exists a morphism $\tilde {\mathcal{P} }\rightarrow \ker \tilde {f}$ by the universality of the kernel. The commutative diagram

(2.10)

descends to the commutative diagram

(2.11)

in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, hence we only have to check the uniqueness of the morphism $h$.

Let $h'\colon {\mathcal {P}}\rightarrow [\ker f']$ be another morphism in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ which fits into the following diagram.

(2.12)

We can lift $h'$ to $\tilde {h}'\colon \tilde {\mathcal{P} }\rightarrow \ker \tilde {f}\langle a\rangle$ for some $a\in \mathbb{R} _{\geqslant 0}$. Take $b\in {\mathbb {R}}_{\geqslant 0}$ so that $T^b\tilde {\iota }\langle a\rangle \circ \tilde {h}'=T^{a+b}\tilde {g}$ is satisfied. Then we again get a commutative diagram.

(2.13)

On the other hand, we have the following commutative diagram.

(2.14)

By the universality of $\ker \tilde {f}\langle a+b\rangle$, we have $T^{a+b}\tilde {h}=T^b\tilde {h}'$. Hence $h=h'$. This completes the proof.

Proof Proof of Proposition 2.6

It remains to show that the isomorphism between $\mathrm {im}$ and $\mathrm {coim}$. Let $f$ be a morphism in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ and $\tilde {f}$ be a lift of $f$. As shown in Lemma 2.12, $\mathrm {im} f$ is given by $[\mathrm {im} \tilde {f}]$ and $\mathrm {coim} f$ is given by $[\mathrm {coim} \tilde {f}]$. Since $\mathrm {Mod}^0(\Lambda _X)$ is abelian, there exists a canonical isomorphism $\mathrm {im}\tilde {f}\cong \mathrm {coim}\tilde {f}$. This also induces an isomorphism between $\mathrm {im} f$ and $\mathrm {coim} f$. This completes the proof.

Corollary 2.13 The functor $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is exact.

Proof. This is obvious from Lemma 2.12.

It is useful to state a kind of the converse of the above corollary.

Lemma 2.14 Let

(2.15)\begin{equation} 0\rightarrow {\mathcal{V}}\xrightarrow{f} {\mathcal{W}}\xrightarrow{g} {\mathcal{X}}\rightarrow 0 \end{equation}

be an exact sequence of $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. Then there exists an exact sequence

(2.16)\begin{equation} 0\rightarrow \tilde{\mathcal{V}}\xrightarrow{\tilde{f}} \tilde{\mathcal{W}}\xrightarrow{\tilde{g}} \tilde{\mathcal{X}}\rightarrow 0 \end{equation}

in $\mathrm {Mod}^0(\Lambda _X)$ which is a lift of the above sequence.

Proof. Take a lift $\tilde {\mathcal{V} }'\xrightarrow {\tilde {f}'}\tilde {\mathcal{W} }\xrightarrow {\tilde {g}'}\tilde {\mathcal{X} }'$ such that $\tilde {g}'\circ \tilde {f}'=0$. Set $\tilde {\mathcal{V} }:=\ker \tilde {g}'$ and $\tilde {\mathcal{X} }:=\operatorname {im} \tilde {g}'$. Then we have an exact sequence

(2.17)\begin{equation} 0\rightarrow \tilde{\mathcal{V}}\xrightarrow{\tilde{f}} \tilde{\mathcal{W}}\xrightarrow{\tilde{g}} \tilde{\mathcal{X}}\rightarrow 0. \end{equation}

Here $\tilde {f}$ and $\tilde {g}$ are canonical morphisms. We have an associated morphism $\tilde {\mathcal{V} }'\rightarrow \tilde {\mathcal{V} }$. In $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$, this associates a morphism $ {\mathcal {V}}\rightarrow [\tilde {\mathcal{V} }]=[\ker \tilde {g}']=\ker g$. By the exactness of the given sequence, we have $ {\mathcal {V}}\xrightarrow {\cong } [\tilde {\mathcal{V} }]$. Hence $\tilde {\mathcal{V} }$ is a lift of $ {\mathcal {V}}$. In a similar way, one can see that $\tilde {\mathcal{X} }$ is a lift of ${\mathcal {X}}$. This completes the proof.

3. The category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D)})$

In this section, we glue up $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ to obtain a modified category, especially for noncompact manifolds.

3.1 Topological space with boundary

We say a topological space is good if it is Hausdorff, locally compact, countable at infinity and has finite flabby dimension. In this paper, a topological space with boundary is a pair $(\bar {X},D_X)$ of a good topological space $\bar {X}$ with a closed subset $D_X$ of $\bar {X}$. We say $D_X$ is the boundary of $({\bar {X}},D_X)$ and ${\bar {X}}{\backslash } D_X$ is the interior of $({\bar {X}},D_X)$. A morphism between $(\bar {X}, D_X)$ and $(\bar {Y}, D_Y)$ is a continuous map $f$ between $\bar {X}$ and $\bar {Y}$ preserving the interiors. We denote the interiors by $X:={\bar {X}}{\backslash } D_X$ and $Y:={\bar {Y}}{\backslash } D_Y$. We also denote the induced map between interiors by $f\colon X\rightarrow Y$ by the abuse of notation.

Example 3.1 (i) Our primary examples of topological spaces with boundaries are of the following class. For a topological space $Z$, consider a locally closed subset $S$. Let $\bar {S}$ be the closure of $S$. Then $(\bar {S}, \bar {S}{\backslash } S)$ is a topological space with boundary. We have a canonical map $(\bar {S}, \bar {S}{\backslash } S)\rightarrow (Z,\varnothing )$ induced by the inclusion $\bar {S}\hookrightarrow Z$.

(ii) By the definition of morphisms of topological spaces with boundary, we have canonical maps $(X,\varnothing )\rightarrow ({\bar {X}}, D_X)$ and ${({\bar {X}}, D_X)}\rightarrow ({\bar {X}}, \varnothing )$ induced by the identity $\operatorname {id}\colon {\bar {X}}\rightarrow {\bar {X}}$. On the other hand, such a canonical map does not exist from ${({\bar {X}}, D_X)}$ to $(X, \varnothing )$.

Let $({\bar {X}}, D_X)$ be a topological space with boundary. The site $\mathrm {Open}_{({\bar {X}}, D_X)}$ is defined by the following data: the underlying category is the category of open subsets of ${\bar {X}}{\backslash } D_X$, a collection of open subsets $\{U_i\}_{i\in I}$ in ${\bar {X}}{\backslash } D_X$ is said to define a cover of $U$ if there exists a subset $J$ of $I$ such that the subcollection $\{U_i\}_{i\in J}$ still defines an open covering of $U$ and is locally finite over ${\bar {X}}$.

Remark 3.2 Here we explain some motivations of the definition of $\mathrm {Open}_{({\bar {X}}, D_X)}$. The essential point is the local finiteness at $D_X$. If one does not introduce this finiteness, after the stackification below, all objects have trivial grading around $D_X$. Since our grading encodes asymptotic behaviors of solutions of irregular ${\mathcal {D}}$-modules, we have to keep nontrivial gradings at $D_X$.

A similar thing occurs even if you consider ind-sheaves. Since ind-sheaves are ind-objects of compactly supported sheaves, ind-sheaves on $X$ cannot encode the data around $D_X$. To consider the data around $D_X$, one has to consider compactly supported sheaves on ${\bar {X}}$ whose stalks can be nonzero only in $X$.

The following is clear.

Lemma 3.3 The cover defined just before Remark 3.2 gives a Grothendieck topology on $\mathrm {Open}_{({\bar {X}}, D_X)}$.

Remark 3.4 If ${\bar {X}}$ is compact and $D_X=\varnothing$ then $\mathrm {Open}_{({\bar {X}},D_X)}$ coincides with the usual site of ${\bar {X}}$.

Lemma 3.5 Let $f\colon ({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$ is a morphism between topological spaces with boundary. Then there exists an induced morphism $\mathrm {Open}_{({\bar {Y}}, D_Y)}\rightarrow \mathrm {Open}_{({\bar {X}}, D_X)}$.

Proof. Let $\{U_i\}_{i\in I}$ be a cover of $U$ in $\mathrm {Open}_{({\bar {Y}}, D_Y)}$. Let $J\subset I$ be as in the definition of the cover. Then $\{f^{-1}(U_i)\}$ is an open covering of $f^{-1}(U)$ in ${\bar {X}}$. Take $x\in {\bar {X}}$, then there exists a small neighborhood $V$ of $f(y)$ such that $V$ only intersects with a finite subset of $\{U_j\}_{j\in J}$. Then $f^{-1}(V)$ also only intersects with a finite subset of $\{f^{-1}(U_j)\}_{j\in J}$. Hence $\{f^{-1}(U_i)\}_{i\in I}$ is a cover of $f^{-1}(U)$ in $\mathrm {Open}_{({\bar {X}}, D_X)}$.

Remark 3.6 The reader may consider the notion of topological spaces with boundary is similar to the notion of bordered spaces in [DK16]. However, the role of these two notions are different: the former is about the base space and the latter is about the additional variable $ {\mathbb {R}}$.

3.2 The category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$

Let $({\bar {X}}, D_X)$ be a topological space with boundary. We set $X:={\bar {X}}{\backslash } D_X$. Let $U\supset V$ be open subsets of $X$. Then we have a restriction functor

(3.1)\begin{equation} \mathrm{Mod}_{pre}^{\mathfrak{I}}(\Lambda_U)\rightarrow \mathrm{Mod}_{pre}^{\mathfrak{I}}(\Lambda_V). \end{equation}

Lemma 3.7 This restriction functor is exact.

Proof. A short exact sequence in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _U)$ can be lifted to a short exact sequence in $\mathrm {Mod}^0(\Lambda _U)$ by Corollary 2.13. Then we can restrict it to an exact sequence in $\mathrm {Mod}^0(\Lambda _V)$. By Lemma 2.12, this also gives an exact sequence in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _V)$.

These maps form a presheaf of categories over the site $\mathrm {Open}_{({\bar {X}},D_X)}$. This is not always a stack (even a prestack) because the tensor product $\otimes \mathbb {k}$ on the hom-space breaks the sheaf property.

Take the stackification (respectively prestackification) of this stack with respect to $\mathrm {Open}_{({\bar {X}},D_X)}$. We denote it by $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ (respectively ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{{({\bar {X}}, D_X)}}$).

Definition 3.8 The global section category of $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}},D_X)}$ is denoted by $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. For a manifold $X$, we set $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X):=\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(X, \varnothing )})$.

Proposition 3.9 The category $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$ is an abelian category for any $U\in \mathrm {Open}_{{({\bar {X}}, D_X)}}$.

Proof. We will only consider the case of kernels. A similar argument holds for cokernels, images and coimages.

Let $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism in $\mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$. Then there exists a covering $\{U_i\}$ of $U$ such that we have a descent data $f_i\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_i)$. If it is necessary, we can replace the covering with a finer covering so that each $f|_{U_i}$ is represented by a morphism $f_{i}\colon {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{i})$. On each intersection $U_{i}\cap U_{j}$, we have a further covering $\{U_{ijk}\}_k$ such that $(f_i-f_j)|_{U_{ijk}}=0$.

Then we have $\ker (f_{i})$ since $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{i}})$ is an abelian category. Since the restriction functors are exact (Lemma 3.7), we have $\ker (f_i|_{U_{ij}})|_{U_{ijk}}=\ker (f_i|_{U_{ijk}})=\ker (f_j|_{U_{ijk}})=\ker (f_j|_{U_{ij}})|_{U_{ijk}}$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_{ijk}})$. Hence we have $\ker (f_i)|_{U_{ij}}=\ker (f_i|_{U_{ij}})=\ker (f_j|_{U_{ij}})=\ker (f_j)|_{U_{ij}}$ in $\mathrm {Mod}^{\mathfrak {I}}_{{({\bar {X}}, D_X)}}(U_{ij})$. This further gives a descent data and glues up to an object ${\mathcal {K}}\in \mathrm {Mod}^{\mathfrak {I}}_{({\bar {X}}, D_X)}(U)$.

For a morphism $g\colon {\mathcal {X}}\rightarrow {\mathcal {V}}$ with $f\circ g=0$, by taking a sufficiently fine cover $\{U_i\}$, we can represent $f, g, {\mathcal {X}}, {\mathcal {V}}$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _{U_i})$. Then one gets a unique factorizing morphism ${\mathcal {X}}|_{U_i}\rightarrow \ker f_i$. Again by taking a finer covering as in the previous part of the proof and the universality, the set of these factorizing morphisms gives a descent data and can be glued up into the unique factorizing ${\mathcal {X}}\rightarrow {\mathcal {K}}$. This shows ${\mathcal {K}}$ is $\ker f$.

Let $U$ be an open subset of $X$. Let $\alpha _U\colon \mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)\rightarrow \mathrm {Mod}^ {\mathfrak {I}}_{({\bar {X}},D)}(U)$ be the canonical functor.

Lemma 3.10 The functor $\alpha _U$ is an exact functor.

Proof. Since kernels, cokernels, images, and coimages are defined locally, the assertion is obvious.

Lemma 3.11 If $\bar {U}$ is compact, the functor $\alpha _U$ is fully faithful.

Proof. We set $D_U:=D_X\cap \bar {U}$. To show the claim, it is enough to prove $\operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _U)}( {\mathcal {V}}, {\mathcal {W}})$ is a sheaf over the site $\mathrm {Open}_{(\bar {U},D_U)}$. Since $\bar {U}$ is compact, any cover in $\mathrm {Open}_{(\bar {U}, D_U)}$ has a finite subcover.

We first assume that there exists a finite cover $\{U_i\}$ of $U$ such that the restriction of $f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$ to each open subset is zero. Let $\tilde {f}\in \operatorname {Hom}_{\mathrm {Mod}^0(\Lambda _X)}(\tilde {\mathcal{V} }, \tilde {\mathcal{W} })$ be a lift. Then the restriction of $f$ to each open subset $U_i$ is represented by $\tilde {f}|_{U_i}$. Since $f|_{U_i}=0$, there exists a $T^a$ such that $T^a\tilde {f}|_{U_i}=0$ by Lemma 2.8. Let $A$ be the maximum of those $a$ values. Then $T^A\tilde {f}=0$. Hence $f=0$.

Let $\{f_{i}\}\in \prod \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}_{pre}(\Lambda _{U_i})}( {\mathcal {V}}|_{U_i}, {\mathcal {W}}|_{U_i})$ satisfy the descent condition. Depending on $i$, we have a set of lifts $\tilde {f}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{W} }|_{U_i}\langle a_i\rangle$ in $\mathrm {Mod}^0(\Lambda _{U_i})$. In our situation, we can take $a_i=a_j$ for any $i,j$, since the indexes are finite. Then we replace $\tilde {\mathcal{W} }$ with $\tilde {\mathcal{W} }\langle a_i\rangle$ by Lemma 2.12. On $U_i\cap U_j$, $\tilde {f}_i$ and $\tilde {f}_j$ may not coincide, but $f_i=[\tilde {f}_i]$ coincides with $f_j=[\tilde {f}_j]$. Hence there exists $T^{a_{ij}}$ such that $T^{a_{ij}}\tilde {f}_i=T^{a_{ij}}\tilde {f}_j$. By taking the maximum among $a_{ij}$, we replace $\tilde {f}_j$ with $T^a \tilde {f}_j$ then the set $\{T^a \tilde {f}_i\}$ satisfies the descent condition in $\mathrm {Mod}^0(\Lambda _U)$. Hence we get a glued morphism.

Corollary 3.12 If $X$ is compact, $\mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$ is an abelian subcategory of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{X})$.

Proof. The embedding is given by the proof of Lemma 3.11.

Let us denote the derived category by $D^{\bullet }(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ ($\bullet =b, \pm$).

3.3 Forgetting shifts

Recall that we have the canonical functor $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}_{pre}(\Lambda _X)$. There also exists a canonical functor $\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.

Lemma 3.13 The functor $\alpha _X\circ [\cdot ]\colon \mathrm {Mod}^0(\Lambda )\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an exact functor.

Proof. This is a consequence of Lemma 3.10 and Corollary 2.13.

For simplicity, we will denote $\alpha _X\circ [\cdot ]$ by $[\cdot ]$. We denote the exact functor $D^\bullet (\mathrm {Mod}^0(\Lambda _X))\rightarrow D^\bullet (\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ induced by $[\cdot ]$ by the same notation.

3.4 Finite limits and finite colimits

Since $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is an abelian category, it admits finite limits and finite colimits.

Lemma 3.14 Let $F\colon {\mathfrak {U}}\rightarrow \mathrm {Mod}^0(\Lambda _X)$ be a finite diagram without loops in $\mathrm {Mod}^0(\Lambda _X)$. We have

(3.2)\begin{equation} \begin{gathered} \big[\lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}[F],\\ \big[\lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}F\big]\cong \lim_{\substack{\longrightarrow \\ {\mathfrak{U}}}}[F]. \end{gathered} \end{equation}

Proof. We will only prove the first equivalence. The second equivalence can be proved in a similar manner.

It is enough to show that the left-hand side satisfies the universality of the right-hand side. Let $ {\mathcal {V}}$ be an object which is over $[F]$. Locally, we have a lift $\tilde {\mathcal{V} }\rightarrow F$. By the universality, we get a morphism $\tilde {\mathcal{V} }\rightarrow \displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F$, which induces a morphism $ {\mathcal {V}}\rightarrow [\displaystyle {\lim _{\substack {\longleftarrow \\ {\mathfrak {U}}}}}F]$ locally. The uniqueness of this morphism can be shown by a method similar to the proof of Lemma 2.12. The uniqueness glue up these local morphisms to obtain the desired result.

Remark 3.15 Contrary to the finite case, infinite (co)limits do not commute with $[\cdot ]$ in general. We give one example in the following. Let us set ${\bar {X}}=[0,\infty )$ and $D_X=\{0\}$. Consider $ {\mathcal {V}}_1:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x\}}$ and $ {\mathcal {V}}_2:={\bigoplus} _{a\in {\mathbb {R}}}\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-a,\infty )}\mathbb {k}_{\{t\geqslant 1/x^2\}}$. As we can see in the discussion of § 5 below, we have $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}([ {\mathcal {V}}_2], [ {\mathcal {V}}_1])=0$. Let $i_b\colon (b,\infty )\hookrightarrow [0, \infty )$ be the open embedding for $b\in {\mathbb {R}}_{>0}$.

If $[\cdot ]$ and colimits commute, we have $[ {\mathcal {V}}_2]\cong \displaystyle {\lim _{\substack {\longrightarrow \\ b\rightarrow 0}}}[i_{b!}i_b^{-1} {\mathcal {V}}_2]$. Again, from the discussion of § 5, we can conclude

(3.3)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}([{\mathcal{V}}_2], [{\mathcal{V}}_1])\cong \lim_{\substack{\longleftarrow \\ b\rightarrow 0}}\operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{V}}_2|_{(b.\infty)}, {\mathcal{V}}_1|_{(b,\infty)})\cong \mathbb{k}. \end{equation}

This is a contradiction.

3.5 Operations

In this section, we will develop the six functors. As above, $({\bar {X}}, D_X), ({\bar {Y}}, D_Y)$ are topological spaces with boundaries. We set $X:={\bar {X}}{\backslash } D_X$ and $Y:={\bar {Y}}{\backslash } D_Y$. In the rest of this section, we use the following notation.

Notation 3.1

• – $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$.

• – ${\mathcal {Y}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$.

• – $\tilde {\mathcal{V} }_U, \tilde {\mathcal{W} }_U, \tilde {\mathcal{X} }_U\in \mathrm {Mod}^0(\Lambda _U)$ are lifts of $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}}$ over $U$.

• – $\{U_i\}_{i\in I}$ is a covering in $\mathrm {Open}_{({\bar {X}}, D_X)}$ with lifts $\{\tilde {\mathcal{V} }_i\}_{i\in I}, \{\tilde {\mathcal{W} }_i\}_{i\in I}, \{\tilde {\mathcal{X} }_i\}_{i\in I}$. Here $\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i, \tilde {\mathcal{X} }_i$ are abbreviations of $\tilde {\mathcal{V} }_{U_i}, \tilde {\mathcal{W} }_{U_i}, \tilde {\mathcal{X} }_{U_i}$ respectively.

• – $\{V_j\}_{j\in J}$ is a covering in $\mathrm {Open}_{({\bar {Y}}, D_Y)}$ with lifts $\{\tilde {\mathcal{Y} }_j\}_{j\in J}$. Here $\tilde {\mathcal{Y} }_j$ are abbreviations of $\tilde {\mathcal{V} }_{U_j}$ respectively.

The internal hom sheaf is defined by the assignment

(3.4)\begin{equation} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}, \tilde{\mathcal{W}})\colon U\mapsto \bigoplus_{a}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_U)}({\mathcal{V}}|_U, {\mathcal{W}}|_U\langle a\rangle) \end{equation}

for an open subset $U\subset X$. This is canonically an $ {\mathbb {R}}$-graded $\Lambda _X$-module.

There exists an open covering $\{U_i\}_{i\in I}$ of $X$ in the site $\mathrm {Open}_{({\bar {X}},D_X)}$ with lifts $\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i$ over each $U_i$. Then one has an $ {\mathbb {R}}$-graded $\Lambda _{U_i}$-module $\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)$ over each $U_i$.

Lemma 3.16 The set $\{[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i, \tilde {\mathcal{W} }_i)]\}$ satisfies the descent and gives an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})$. This is independent of the choice of local lifts.

Proof. On $U_{ij}:=U_i\cap U_j$, we have the isomorphism $f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$ in ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. Then there exists an open covering $\{U_{ijk}\}$ of $U_{ij}$ where there exists a descent data $f_{ijk}\colon [\tilde {\mathcal{V} }_i|_{U_{ijk}}]\rightarrow [\tilde {\mathcal{V} }_j|_{U_{ijk}}]$ for the isomorphism $f\colon [\tilde {\mathcal{V} }_i|_{U_{ij}}] \rightarrow [\tilde {\mathcal{V} }_j|_{U_{ij}}]$.

We can take a lift $\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle$ of this morphism and that of the inverse $\tilde {g}_{ijk}\colon \tilde {\mathcal{V} }_j|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_i|_{U_{ijk}}\langle b\rangle$ for some $a, b$. The difference $\tilde {g}_{ijk}\langle a\rangle \circ \tilde {f}_{ijk}-T^{a+b}$ and $\tilde {f}_{ijk}\langle b\rangle \circ \tilde {g}_{ijk}-T^{a+b}$ becomes $0$ after multiplying $T^c$ for sufficiently big $c$ by Lemma 2.8.

For simplicity, let us assume that ${\mathcal {W}}$ has a global lift, i.e. ${\mathcal {W}}=[\tilde {\mathcal{W} }]$, although we can do the same for general ${\mathcal {W}}$. We have the following induced morphisms:

(3.5)\begin{equation} \begin{gathered} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\xrightarrow{p(\tilde{g}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -b\rangle, \\ \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_j|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}}), \xrightarrow{p(\tilde{f}_{ijk})} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i|_{U_{ijk}}, \tilde{\mathcal{W}}|_{U_{ijk}})\langle -a\rangle, \end{gathered} \end{equation}

where $p(\tilde {f}_{ijk})$ and $p(\tilde {g}_{ijk})$ are precompositions of $f$ and $g$. Since $p(\tilde {f}_{ijk})\langle a\rangle \circ p(\tilde {g}_{ijk})-T^{a+b}\operatorname {id}$ and $p(\tilde {g}_{ijk})\circ p(\tilde {f}_{ijk})\langle b\rangle -T^{a+b}\operatorname {id}$ vanish by multiplying $T^c$ for big $c$, we can conclude $[\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_i|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]\cong [\mathop {{{\mathcal {H}}}om}\nolimits (\tilde {\mathcal{V} }_j|_{U_{ijk}}, \tilde {\mathcal{W} }|_{U_{ijk}})]$. A similar argument as was done in Proposition 3.9 gives a gluing of these isomorphisms to give a global object in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The independence of the choice of local lifts is also clear.

Let us consider the assignment

(3.6)\begin{equation} V\mapsto \tilde{\mathcal{V}}_U(V)\otimes_\Lambda \mathbb{k} \end{equation}

for $V\subset U\in \mathrm {Open}_{({\bar {X}}, D_X)}$. Then this assignment does not depend on the choice of the lift $\tilde {\mathcal{V} }_U$. Hence one can associate a sheaf over $\mathrm {Open}_{({\bar {X}}, D_X)}$. We write it $ {\mathcal {V}}\otimes \mathbb {k}$.

Lemma 3.17 The sheaf $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\otimes \mathbb {k}$ over $\mathrm {Open}_{({\bar {X}}, D_X)}$ is canonically isomorphic to $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}_{\Lambda _{({\bar {X}}, D_X)}}}( {\mathcal {V}}, {\mathcal {W}})$.

Proof. This is obvious from the construction.

For $ {\mathbb {R}}$-graded $\Lambda$-modules $V$ and $W$, their tensor product is defined as follows:

(3.7)\begin{equation} \operatorname{Gr}^a(V\otimes_\Lambda W):=\bigoplus_{b+c=a}\operatorname{Gr}^bV\otimes_k \operatorname{Gr}^cW/{\sim}, \end{equation}

where the equivalence relations are generated by

(3.8)\begin{equation} v\otimes_k \alpha w\sim \alpha v\otimes_k w, \end{equation}

where $\alpha \in \Lambda , v\in V, w\in W$ are homogeneous and $\operatorname {deg} \alpha +\operatorname {deg} v+\operatorname {deg} w=a$. The tensor product $V\otimes _\Lambda W:={\bigoplus} _a \operatorname {Gr}^a(V\otimes _\Lambda W)$ is canonically equipped with a $\Lambda$-module structure.

Then the tensor product $\tilde {\mathcal{V} }\otimes \tilde {\mathcal{W} }$ is defined by the sheafification of the assignment

(3.9)\begin{equation} \tilde{\mathcal{V}}\otimes_{\Lambda_X} \tilde{\mathcal{W}}\colon U\mapsto \tilde{\mathcal{V}}(U)\otimes_\Lambda\tilde{\mathcal{W}}(U). \end{equation}

One has another $ {\mathbb {R}}$-graded $\Lambda _{U_i}$-module $\tilde {\mathcal{V} }_i\otimes _{\Lambda _X} \tilde {\mathcal{W} }_i$ over each $U_i$.

Lemma 3.18 The set $\{[\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\tilde {\mathcal{W} }_i]\}$ satisfies the descent and gives an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, which we will denote by $ {\mathcal {V}}\otimes {\mathcal {W}}$. This is independent of the choice of local lifts.

Proof. We can prove in a similar manner as in the proof of Lemma 3.16.

Proposition 3.19 We have the following:

(3.10)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}})\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}})). \end{equation}

Proof. We have a canonical isomorphism

(3.11)\begin{equation} \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i\otimes \tilde{\mathcal{W}}_i, \tilde{\mathcal{X}}_i)\cong \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}_i, \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{W}}_i,\tilde{\mathcal{X}}_i)). \end{equation}

By tensoring $\mathbb {k}$ and taking sheafification over $\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$, we have an isomorphism

(3.12)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{({\bar{X}}, D_X)}}({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}})\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{({\bar{X}}, D_X)}}({\mathcal{V}},\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}}, {\mathcal{X}})) \end{equation}

as a sheaf over $\mathrm {Open}_{(\overline {U_i}, \overline {U_i}\cap D_X)}$. The isomorphisms over the $U_i$ are glued up and give a desired result.

Corollary 3.20 In the same setting as above, we have the following:

(3.13)\begin{equation} \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}})\cong \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}})). \end{equation}

Proof. From the above proposition, we have

(3.14)\begin{align} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}\otimes {\mathcal{W}}, {\mathcal{X}}))&\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}\otimes {\mathcal{W}} ,{\mathcal{X}})\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}}\otimes {\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{Y}},\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{V}}, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{W}},{\mathcal{X}}))). \end{align}

Yoneda's lemma implies the desired statement.

We will define push-forwards for a class of morphisms.

In the following, we only consider the following class of maps.

Definition 3.21 We say a morphism $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ is tame if the underlying map $f\colon {\bar {X}}\rightarrow {\bar {Y}}$ is proper.

Remark 3.22 For a locally closed subset $U\subset X$, a canonical morphism $(U, \varnothing )\rightarrow (X, \varnothing )$ is not tame in general. However $(\bar {U}, \bar {U}{\backslash } U)\rightarrow (X, \varnothing )$ is tame. In this sense, we will consider the latter one as a standard inclusion morphism.

Let $f$ be a tame map $({\bar {X}}, D_X)\rightarrow ({\bar {Y}}, D_Y)$. We first assume that $ {\mathcal {V}}$ has $\tilde {\mathcal{V} }$ with $[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set

(3.15)\begin{equation} f_*{\mathcal{V}}:=[f_*\tilde{\mathcal{V}}], \end{equation}

where push-forward of $ {\mathbb {R}}$-graded $\Lambda _X$-module $\tilde {\mathcal{V} }$ is defined by $\operatorname {Gr}^af_*\tilde {\mathcal{V} }:=f_*\operatorname {Gr}^a\tilde {\mathcal{V} }$.

Lemma 3.23 This is well defined.

Proof. Let $\tilde {\mathcal{V} }'$ be another lift. Take a covering $\{U_i\}$ of $\mathrm {Open}_{({\bar {X}}, D_X)}$ such that we have lifts of the isomorphisms $\tilde {g}_i\colon \tilde {\mathcal{V} }|_{U_i}\rightarrow \tilde {\mathcal{V} }'\langle a_i\rangle |_{U_i}$ and $\tilde {h}_i\colon \tilde {\mathcal{V} }'|_{U_i}\rightarrow \tilde {\mathcal{V} }|_{U_i}\langle b\rangle$ over each $U_i$. Hence $\tilde {g}_i\langle b\rangle \circ \tilde {h}_i-T^{a+b}$ and $\tilde {h}_i\langle a\rangle \circ \tilde {g}_i-T^{a+b}$ vanish by large $T^c$. By pushing forward these equations, we have

(3.16)\begin{equation} 0=f_*(T^c(\tilde{g}\langle b\rangle\circ\tilde{h}-T^{a+b}\operatorname{id}_{\tilde{\mathcal{V}}}))=T^c(f_*\tilde{g}\langle b\rangle\circ f_*\tilde{h}-T^{a+b}\operatorname{id}_{f_*\tilde{\mathcal{V}}}). \end{equation}

Hence we have $[f_*\iota _{i*}\tilde {\mathcal{V} }|_{U_i}]\cong [f_*\iota _{i*}\tilde {\mathcal{V} }'|_{U_i}]$ where $\iota _i\colon U_i\rightarrow X$ is the inclusion map.

Let $ {\mathfrak {U}}$ be the Cech nerve of $\{U_i\}$ and $\iota _U$ for $U\in {\mathfrak {U}}$ the inclusion map. Since $f$ is tame, $\{f(U_i)\}$ is locally finite in ${\bar {Y}}$ i.e. there exists a covering of $Y$ in $\mathrm {Open}_{({\bar {Y}}, D_Y)}$ such that there are only finite $U_i$ in each open subset. Hence we have

(3.17)\begin{equation} \lim_{\substack{\longleftarrow \\ _{U\in {\mathfrak{U}}}}}[f_*\iota_{U*}\tilde{\mathcal{V}}_U]\cong \big[\lim_{\substack{\longleftarrow \\ _{U\in {\mathfrak{U}}}}}f_*\iota_{U*}\tilde{\mathcal{V}}_U\big]\cong [f_*\tilde{\mathcal{V}}] \end{equation}

by Lemma 3.14. Combining with the first part of the proof, we get an isomorphism $[f_*\tilde {\mathcal{V} }]\cong [f_*\tilde {\mathcal{V} }']$.

Since $f$ is tame, there exists a covering $\{V_i\}$ of $Y$ and a finite cover $\{U_{ij}\}$ of each $f^{-1}(V_i)$ with lifts $\tilde {\mathcal{V} }_{ij}$ of $ {\mathcal {V}}$.

Let $ {\mathfrak {U}}_i$ be the Cech nerve of $\{U_{ij}\}$. We set

(3.18)\begin{equation} (f_*{\mathcal{V}})_i:=\lim_{\substack{\longleftarrow \\ _{U\in {\mathfrak{U}}_i}}}[f_*\iota_{U*}\tilde{\mathcal{V}}_U]. \end{equation}

Lemma 3.24 The collection $\{(f_* {\mathcal {V}})_i\}$ gives an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y)$, denoted by $f_* {\mathcal {V}}$. Moreover, it does not depend on the choice of coordinates and lifts.

Proof. It can be proved by a similar argument as in Lemma 3.23.

Over $f^{-1}(V_i)$, we assign a sheaf $[f^{-1}\tilde {\mathcal{Y} }_i]$ and these can glue up together. We will denote the resulting object by $f^{-1}{\mathcal {Y}}$.

Lemma 3.25 We have the following natural isomorphism:

(3.19)\begin{equation} f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{Y}}, {\mathcal{V}})\simeq \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{Y}}, f_*{\mathcal{V}}). \end{equation}

Proof. It is enough to prove the statement over each $V_i$. There exists a finite covering $\{U_j\}$ of $f^{-1}(V_i)$ with lifts $\{\tilde {\mathcal{W} }_j\}$. Then $\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1} {\mathcal {V}}, {\mathcal {W}})$ is represented by $\{\mathop {{{\mathcal {H}}}om}\nolimits (f^{-1}\tilde {\mathcal{V} }_i|_{U_j}, \tilde {\mathcal{W} }_j)\}$.

Let $ {\mathfrak {U}}$ be the Cech nerve of $\{U_j\}$. By the definition of the push forward, we have

(3.20)\begin{equation} f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{Y}}, {\mathcal{V}})|_{V_i}\simeq \lim_{\substack{\longleftarrow \\ U\in {\mathfrak{V}}}}([f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)]). \end{equation}

Here $\tilde {\mathcal{V} }|_U$ means $\tilde {\mathcal{V} }_i|_U$ for some $U\subset U_i$. We also have

(3.21)\begin{align} f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)&\simeq f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}\tilde{\mathcal{Y}}_i, i_{U*}\tilde{\mathcal{V}}|_U)\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{Y}}_i, f_*\iota_{U*}\tilde{\mathcal{V}}|_U) \end{align}

for $U\in {\mathfrak {U}}$. Hence

(3.22)\begin{align} \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}}([f_*i_{U*}\mathop{{{\mathcal{H}}}om}\nolimits((f^{{-}1}\tilde{\mathcal{Y}}_i)|_{U}, \tilde{\mathcal{V}}|_U)])&\simeq \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*\iota_{U*}\tilde{\mathcal{V}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], \lim_{\substack{\longleftarrow \\ {\mathfrak{U}}}} [f_*\iota_{U*}\tilde{\mathcal{W}}|_U])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{Y}}_i], [f_*(\tilde{\mathcal{V}}|_{f^{{-}1}(V_i)})])\nonumber\\ &\simeq \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{Y}}, f_*{\mathcal{V}})|_{V_i}. \end{align}

This completes the proof.

Lemma 3.26 We have

(3.23)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})}(f^{{-}1}{\mathcal{V}},{\mathcal{W}})\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})}({\mathcal{V}}, f_*{\mathcal{W}}). \end{equation}

Proof. Taking $\otimes \mathbb {k}$ and the global sections (as in the paragraph above Lemma 3.17) of both sides of Lemma 3.25, the right-hand side becomes $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})}( {\mathcal {V}}, f_*{\mathcal {W}})$ and the left-hand side becomes

(3.24)\begin{align} (f_*\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}) \otimes \mathbb{k}) (Y)&\cong f_*(\mathop{{{\mathcal{H}}}om}\nolimits(f^{{-}1}{\mathcal{V}},{\mathcal{W}})\otimes \mathbb{k}) (Y)\nonumber\\ &\cong \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{({\bar{X}}, D_X)}}(f^{{-}1}{\mathcal{V}}, {\mathcal{W}}). \end{align}

This completes the proof.

We first assume that $ {\mathcal {V}}$ has $\tilde {\mathcal{V} }$ with $[\tilde {\mathcal{V} }]\cong {\mathcal {V}}$. In this case, we simply set

(3.25)\begin{equation} f_!{\mathcal{V}}:=[f_!\tilde{\mathcal{V}}]. \end{equation}

Lemma 3.27 This is well defined.

Proof. This can be proved in the same way as the proof of Lemma 3.23.

Again by the same construction as in the case of push-forwards, we can define $f_! {\mathcal {V}}$ in general under the assumption of tameness.

Assumption 3.28 In the following, when we consider $f_*$ or $f_!$, we always assume the tameness of $f$.

4. Derived category of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$

4.1 Injectives and flats

In this section, we develop fundamentals about derived operations for $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. In this section, we will use Notation 3.1.

Lemma 4.1 Let ${\mathcal {F}}$ be an $ {\mathbb {R}}$-graded $\Lambda$-module. For $x\in X$, the skyscraper sheaf $[{\mathcal {F}}_x]$ is an injective object. Moreover, the product $[\prod _{x\in V}{\mathcal {F}}_x]$ for a subset $V\subset X$ is also an injective object.

Proof. The first part is almost trivial. Let us prove the second part.

Let $0\rightarrow {\mathcal {V}}\xrightarrow {f} {\mathcal {W}}$ be an injection in the category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ with a map $ {\mathcal {V}}\xrightarrow {g} [\prod _{x\in X}{\mathcal {F}}_x]$. Let us take a locally finite covering $\{U_i\}$ of $X$ with lifts $0\rightarrow \tilde {\mathcal{V} }_i\xrightarrow {\tilde {f}_i} \tilde {\mathcal{W} }_i$ and $\tilde {\mathcal{V} }_i\xrightarrow {\tilde {g}_i} \prod _{x\in U_i}{\mathcal {F}}_x\langle a_i\rangle $. We also get a lift $\tilde {\mathcal{W} }_i\xrightarrow {\tilde {h}_i}\prod _{x\in U}{\mathcal {F}}_x\langle a_i\rangle $.

For each $x\in V$, we choose $i_x$ from finite candidates of $i$ values satisfying $x\in U_i$. We set $\tilde {\mathcal{W} }_x:=(\tilde {\mathcal{W} }_{i_x})_x$. Over each $U_i$, the morphism $\tilde {h}_i$ gives an element of $({\bigoplus} _{a\in {\mathbb {R}}}\prod _{x\in U_i}\operatorname {Hom}^{a}(\tilde {\mathcal{W} }_{x}, {\mathcal {F}}_x))\otimes _\Lambda k\cong \operatorname {Hom}(W|_{U_i}, [\prod _{x\in V}{\mathcal {F}}_x])$ which is zero on $i_x\neq i$. Then they are trivially glued up to give a desired lift of $g$.

Proposition 4.2 The category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}},D_X)})$ has enough injectives.

Proof. As usual, one can embed $\tilde {\mathcal{V} }_i$ to an injective object $\tilde {\mathcal{I} }_i$ which is a product of skyscraper sheaves.

Hence we have the inclusion $[\tilde {\mathcal{V} }_i]\hookrightarrow [\tilde {\mathcal{I} }_i]$. This induces the inclusion $ {\mathcal {V}}\hookrightarrow {\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$, where the latter is a locally finite direct sum hence it exits. By Lemma 4.1, ${\bigoplus} [\iota _{i*}\tilde {\mathcal{I} }_i]$ is also an injective object. This completes the proof.

The above proof also shows the following.

Corollary 4.3 There exists an injective resolution $\tilde {\mathcal{I} }^\bullet :=\tilde {\mathcal{I} }^0\rightarrow \tilde {\mathcal{I} }^1\rightarrow \cdots$ of $\tilde {\mathcal{V} }$ giving an injective resolution $[\tilde {\mathcal{I} }^\bullet ]$ of $[\tilde {\mathcal{V} }]$.

Proof. This follows from the fact that $[\cdot ]$ is an exact functor (Lemma 3.13) and Lemma 4.1.

Lemma 4.4 Let $\tilde {\mathcal{F} }$ be a flat $ {\mathbb {R}}$-graded $\Lambda$-module. Then $[\tilde {\mathcal{F} }]$ is a flat object.

Proof. Let $ {\mathcal {V}}\rightarrow {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an injection. Let us take an open covering $\{U_i\}$ of $X$ with lifts $\{\tilde {\mathcal{V} }_i\}$, $\{\tilde {\mathcal{W} }_i\}$ and $\tilde {f}_i\colon \tilde {\mathcal{V} }_i\rightarrow \tilde {\mathcal{W} }_i$. Here one can take $\tilde {f}_i$ as an injection by Lemma 2.14. Then $ {\mathcal {V}}\otimes [\tilde {\mathcal{F} }]$ (respectively ${\mathcal {W}}\otimes [\tilde {\mathcal{F} }]$) is represented by $\tilde {\mathcal{V} }_i\otimes \tilde {\mathcal{F} }|_{U_i}\rightarrow \tilde {\mathcal{W} }_i\otimes \tilde {\mathcal{F} }|_{U_i}$, which is an injection. Then by Lemma 2.12, the morphism $f\otimes [\tilde {\mathcal{F} }]$ is also an injection. This completes the proof.

Proposition 4.5 The category $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$ has enough flats.

Proof. By the same construction as in [KS90, Proposition 2.4.12], there exists a flat object $\tilde {\mathcal{F} }_i$ with a surjection $\tilde {\mathcal{F} }_i\rightarrow \tilde {\mathcal{V} }_i$. Let $\iota _i\colon U_i\hookrightarrow X$ be the open imbedding. Hence $[\iota _{i!}\tilde {\mathcal{F} }_i]$ is also a flat object by Lemma 4.4 and we have a surjection ${\bigoplus} _i[\iota _{i!}\tilde {\mathcal{F} }_i]\rightarrow {\mathcal {V}}$. This completes the proof.

By a similar argument as in Corollary 4.3, we get the following.

Corollary 4.6 For $\tilde {\mathcal{V} }\in \mathrm {Mod}^0(\Lambda _X)$, a flat resolution $\tilde {\mathcal{F} }^\bullet :=\tilde {\mathcal{F} }^0\leftarrow \tilde {\mathcal{F} }^{-1}\leftarrow \cdots$ of $\tilde {\mathcal{V} }$ gives a flat resolution $[\tilde {\mathcal{F} }^\bullet ]$ of $[\tilde {\mathcal{V} }]$.

4.2 Derived functors

Note that right and left exactness of various functors $f_*, f_!, f^{-1}, \mathop {{{\mathcal {H}}}om}\nolimits , \otimes$ are the same as in the case of $\mathbb {k}$-modules, according to Lemma 2.8.

We will use the following ‘derived’ notation of Notation 3.1.

Notation 4.1

• – $ {\mathcal {V}}, {\mathcal {W}}, {\mathcal {X}} \in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}}))$, ${\mathcal {Y}}, {\mathcal {Y}}_1, {\mathcal {Y}}_2\in D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))$.

• – $\tilde {\mathcal{V} }, \tilde {\mathcal{W} }, \tilde {\mathcal{X} }\in D^b(\mathrm {Mod}^0(\Lambda _X))$, $\tilde {\mathcal{Y} }\in D^b(\mathrm {Mod}^0(\Lambda _Y))$.

Lemma 4.7 We have

\[ [\mathbb{R} f_* \tilde {\mathcal{V} }]\simeq {\mathbb {R}} f_*[\tilde {\mathcal{V}}],\quad [\mathbb{R} f_!\tilde {\mathcal{V} }]\simeq {\mathbb {R}} f_![\tilde {\mathcal{V} }] \quad {and}\quad [\mathbb{R} \mathcal{H} om(\tilde {\mathcal{W} }, \tilde {\mathcal{V} })]\simeq {\mathbb{R} \mathcal{H} om}([\tilde {\mathcal{W} }], [\tilde {\mathcal{V} }]). \]

Proof. Since $[\cdot ]$ is an exact functor, it suffices to show the statements for an object $\mathrm {Mod}^0(\Lambda _X)$ by a standard argument in homological algebra. Then $\tilde {\mathcal{V} }$ has an injective resolution $\tilde {\mathcal{I} }^\bullet$ such that $[\tilde {\mathcal{I} }^\bullet ]$ is an injective resolution of $[\tilde {\mathcal{V} }]$ by Corollary 4.3. For $F\in \{f_*, f_!, \mathop {{{\mathcal {H}}}om}\nolimits ([\tilde {\mathcal{W} }], -)\}$, we have

(4.1)\begin{equation} [{\mathbb{R}} F(\tilde{\mathcal{V}})]\simeq [F(\tilde{\mathcal{I}}^\bullet)]\simeq F[\tilde{\mathcal{I}}^\bullet]\simeq {\mathbb{R}} F([\tilde{\mathcal{V}}]). \end{equation}

This completes the proof.

Lemma 4.8 We have $[f^{-1}\tilde {\mathcal{Y} }]\simeq f^{-1}[\tilde {\mathcal{Y} }]$.

Proof. It follows from the definition of $f^{-1}$ and its exactness on $\mathrm {Mod}^0(\Lambda _Y)$.

Lemma 4.9 We have $[\tilde {\mathcal{V} }\otimes ^{\mathbb{L} }\tilde {\mathcal{W} }]\simeq [\tilde {\mathcal{V} }]\otimes ^{\mathbb{L} } [\tilde {\mathcal{W} }]$.

Proof. One can prove by the same argument as in Lemma 4.7 by using Corollary 4.6.

Lemma 4.10 There exists the following isomorphism

(4.2)\begin{equation} {\mathbb{R}\mathcal{H} om}({\mathcal{V}}\otimes^{\mathbb{L}} {\mathcal{W}}, {\mathcal{X}})\simeq {\mathbb{R}\mathcal{H} om}({\mathcal{V}}, {\mathbb{R}\mathcal{H} om}({\mathcal{W}}, {\mathcal{X}})). \end{equation}

Proof. This can be proved by a standard argument. Let us take a flat resolution ${\mathcal {F}}$ of ${\mathcal {W}}$ and an injective resolution ${\mathcal {I}}$ of ${\mathcal {X}}$. Then ${\mathbb{R} \mathcal{H} om}({\mathcal {F}}, {\mathcal {I}})\simeq \mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {F}}, {\mathcal {I}})$ is again an injective object. Actually, we have

(4.3)\begin{equation} \mathop{{{\mathcal{H}}}om}\nolimits(-, \mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{F}}, {\mathcal{I}})))\cong \mathop{{{\mathcal{H}}}om}\nolimits((-)\otimes {\mathcal{F}}, {\mathcal{I}}) \end{equation}

by Proposition 3.19. Then both sides of the equality in the statement is quasi-isomorphic to $\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}\otimes {\mathcal {F}}, {\mathcal {I}})$. This completes the proof.

Lemma 4.11 There exists the following isomorphism

(4.4)\begin{equation} {\mathbb{R}} f_*{\mathbb{R}\mathcal{H} om}(f^{{-}1}{\mathcal{Y}}, {\mathcal{V}})\simeq {\mathbb{R}\mathcal{H} om}({\mathcal{Y}}, {\mathbb{R}} f_*{\mathcal{V}}). \end{equation}

Proof. By Lemma 3.26 and the exactness of $f^{-1}$ imply that push-forward of an injective is again injective. Also, pull-back of a flat object is again flat. Let ${\mathcal {F}}$ be a flat resolution of ${\mathcal {Y}}$ and ${\mathcal {I}}$ be an injective resolution of $ {\mathcal {V}}$. By replacing with these resolutions, we can work with underived functors, then Lemma 3.25 completes the proof.

To construct exceptional inverse image, we follow the argument in [KS90, 3.1].

Assume that $f_!\colon \mathrm {Mod}({\mathbb {Z}}_X)\rightarrow \mathrm {Mod}({\mathbb {Z}}_Y)$ has finite cohomological dimension. Let $\tilde {\mathcal{Z} }$ be an object of $\mathrm {Mod}^0(\Lambda _Y)$ and $K$ be a flat $f$-soft ${\mathbb {Z}}_X$-module. We define a presheaf by

(4.5)\begin{equation} (\operatorname{Gr}^a(f^!_K\tilde{\mathcal{Z}}))(U):=\Gamma(U, \mathop{{{\mathcal{H}}}om}\nolimits^a_{\Lambda_X}(f_!(\Lambda_X\otimes_{{\mathbb{Z}}_X}K_U), \tilde{\mathcal{Z}})). \end{equation}

This is actually a sheaf by [KS90, Lemma 3.1.3]. We set $f^!_K\tilde {\mathcal{V} }:={\bigoplus} _{a\in {\mathbb {R}}}\operatorname {Gr}^a(f^!_K\tilde {\mathcal{V} })$ which is an object of $\mathrm {Mod}^0(\Lambda _X)$. Let us moreover suppose $\tilde {\mathcal{Z} }$ be an injective object.

Lemma 4.12 Under the above assumption, we have the following.

1. (i) The object $f_K^!\tilde {\mathcal{Z} }$ is an injective object of $\mathrm {Mod}^0(\Lambda _{X})$.

2. (ii) For any $\tilde {\mathcal{A} }\in \mathrm {Mod}^0(\Lambda _{X})$. we have a canonical isomorphism

   (4.6)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_Y)}(f_!(\tilde{\mathcal{A}}\otimes_{\mathbb{Z}} K), \tilde{\mathcal{Z}})\xrightarrow{\simeq}\operatorname{Hom}_{\mathrm{Mod}^0(\Lambda_X)}(\tilde{\mathcal{A}}, f^!_K\tilde{\mathcal{Z}}). \end{equation}

Proof. This is done by the same argument as in the proof of [KS90, Lemma 3.1.3].

In the following, we will use $K$ for the following complex.

Lemma 4.13 [KS90, Proposition 3.1.4]

The sheaf ${\mathbb {Z}}_X$ admits a finite flat $f$-soft resolution $K$.

Let $K^+(\mathrm {Mod}^0(\Lambda _X))$ be the homotopy category of injective complexes bounded below of objects in $\mathrm {Mod}^0(\Lambda _X)$. Then we have an equivalence $D^+(\mathrm {Mod}^0(\Lambda _X))\cong K^+(\mathrm {Mod}^0(\Lambda _X))$. We set the composition

(4.7)\begin{equation} f^!\colon D^b(\mathrm{Mod}^0(\Lambda_X))\hookrightarrow K^+(\mathrm{Mod}^0(\Lambda_X))\xrightarrow{f^!_K}K^+(\mathrm{Mod}^0(\Lambda_Y))\xrightarrow{\cong} D^+(\mathrm{Mod}^0(\Lambda_Y)). \end{equation}

Lemma 4.14 The functor $f^!$ is the right adjoint of $ {\mathbb {R}} f_!$. We moreover have

(4.8)\begin{equation} {\mathbb{R}\mathcal{H} om}({\mathbb{R}} f_!\tilde{\mathcal{V}}, \tilde{\mathcal{W}})\cong {\mathbb{R}} f_*{\mathbb{R}\mathcal{H} om}(\tilde{\mathcal{V}}, f^!\tilde{\mathcal{W}}). \end{equation}

Proof. For $\tilde {\mathcal{W} }\in K^+(\mathrm {Mod}^0(\Lambda _X))\cong D^+(\mathrm {Mod}^0(\Lambda _X))$, we have

(4.9)\begin{equation} \operatorname{Hom}_{K^+(\mathrm{Mod}^0(\Lambda_X))}(f_!(\tilde{\mathcal{W}}\otimes_{{\mathbb{Z}}_Y}K), \tilde{\mathcal{V}})\cong \operatorname{Hom}_{K^+(\mathrm{Mod}^0(\Lambda_X))}(\tilde{\mathcal{W}}, f^!\tilde{\mathcal{V}}) \end{equation}

by the above lemma. Since $f_!\tilde {\mathcal{W} }\otimes K\simeq {\mathbb {R}} f_!\tilde {\mathcal{W} }$, we complete the proof of the first assertion. The second assertion can also be proved by the argument of the proof of [KS90, Proposition 3.1.10].

Let us now discuss the exceptional inverse image in $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$. Let ${\mathcal {Z}}$ be an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and $K$ be a ${\mathbb {Z}}_X$-module.

Take a locally finite covering $\{V_i\}$ of $Y$ with lifts $\{\tilde {\mathcal{Z} }_i\}$. Hence we get $f_K^!\tilde {\mathcal{Z} }_i$.

Lemma 4.15 The data $\{[f_K^!\tilde {\mathcal{Z} }_i]\}$ gives an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. We denote the resulting object by $f^!_K{\mathcal {Z}}$.

Proof. Over $V_{ij}:=V_i\cap V_j$, we have $f_{ij}\colon [\tilde {\mathcal{Z} }_i]|_{V_{ij}}\xrightarrow {\cong } [\tilde {\mathcal{Z} }_j]|_{V_{ij}}$. We can lift this map to $\tilde {f}_{ij}\colon \tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow \tilde {\mathcal{Z} }_j\langle a_{ij}\rangle |_{V_{ij}}$ (by taking a refined covering if necessary). We also have a lift of the inverse map $\tilde {f}_{ji}$. Then $\tilde {f}_{ij}\circ \tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id}$ vanishes by multiplying some $T^a$. The map $\tilde {f}_{ij}$ induces a map $f_K^!\tilde {f}_{ij}\colon f^!_K\tilde {\mathcal{Z} }_i|_{V_{ij}}\rightarrow f^!_K\tilde {\mathcal{Z} }_j|_{V_{ij}}$. Then we also have $f_K^!\tilde {f}_{ji}$. Then $f_K^!\tilde {f}_{ij}\circ f_K^!\tilde {f}_{ji}-T^{a_{ij}+{a_{ji}}}\operatorname {id}=f_K^!(\tilde {f}_{ij}\tilde {f}_{ji}-T^{a_{ij}+a_{ji}}\operatorname {id})$ also vanishes by multiplying $T^a$. This completes the proof.

Since $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ has injective resolutions, we have an equivalence $K^{+}(\Lambda _Y)\cong D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))$ where the left-hand side is the homotopy category of complexes bounded below of injective objects. We denote the composition $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _Y))\hookrightarrow K^{+}(\Lambda _Y)\xrightarrow {f^!_K}D^+(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by the notation $f^!$.

Proposition 4.16 The functor $f^!$ is an exact functor.

Proof. The exactness easily follows from the exactness of $f^!$ on $D^b(\mathrm {Mod}^0(\Lambda _Y))$.

Proposition 4.17 We have $f^![\tilde {\mathcal{V} }]\cong [f^!\tilde {\mathcal{V} }]$.

Proof. Replace $\tilde {\mathcal{V} }$ be an injective complex given in Lemma 4.1. Then $[\tilde {\mathcal{V} }]$ is also an injective complex. By the definition of $f^!$ for $\mathrm {Mod}^0(\Lambda _X)$ and $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we have $[f^!\tilde {\mathcal{V} }]\cong [f^!_K\tilde {\mathcal{V} }]\cong f^!_K[\tilde {\mathcal{V} }]\cong f^![\tilde {\mathcal{V} }]$. This completes the proof.

Proposition 4.18 There exists a functorial isomorphism:

(4.10)\begin{equation} \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)}))}({\mathbb{R}} f_!{\mathcal{V}},{\mathcal{Y}})\cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, f^!{\mathcal{Y}}). \end{equation}

Proof. First, note that $ {\mathbb {R}} f_! {\mathcal {V}}\simeq f_!( {\mathcal {V}}\otimes K)$ which is deduced from the local consideration. Let ${\mathcal {I}}$ be an injective resolution of ${\mathcal {Y}}$ and $C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ be the category of bounded complexes of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. Then the left-hand side of the desired equality is

(4.11)\begin{equation} \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})}(f_!({\mathcal{V}}\otimes K), {\mathcal{I}})\cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, f^!{\mathcal{I}}). \end{equation}

We also have a morphism

(4.12)\begin{equation} \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, f^!{\mathcal{Y}})\rightarrow \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, f^!{\mathcal{I}}) \end{equation}

coming from the morphism ${\mathcal {Y}}\rightarrow {\mathcal {I}}$. We would like to prove this is an isomorphism. Let us work locally on $Y$. From the construction in Proposition 4.2, the complex ${\mathcal {I}}$ is coming from an injective object $\tilde {\mathcal{I} }$ locally. Hence we have an isomorphism

(4.13)\begin{equation} \mathop{{{\mathcal{H}}}om}\nolimits([\tilde{\mathcal{V}}], f^![\tilde{\mathcal{I}}])\cong [\mathop{{{\mathcal{H}}}om}\nolimits(\tilde{\mathcal{V}}, f^!\tilde{\mathcal{I}})]\cong [{\mathbb{R}\mathcal{H} om}(\tilde{\mathcal{V}}, f^!\tilde{\mathcal{I}})]\cong {\mathbb{R}\mathcal{H} om}({\mathcal{V}}, f^!{\mathcal{Y}}). \end{equation}

Here we used the fact that $[\cdot ]$ is exact and $f^!\tilde {\mathcal{I} }$ is injective. Then Lemma 4.21 completes the proof.

Proposition 4.19 There exists a functorial isomorphism:

(4.14)\begin{equation} {\mathbb{R}\mathcal{H} om}({\mathbb{R}} f_!{\mathcal{V}}, {\mathcal{Y}})\simeq {\mathbb{R}} f_*{\mathbb{R}\mathcal{H} om}({\mathcal{V}}, f^!{\mathcal{Y}}). \end{equation}

Proof. As usual sheaves, we have a canonical morphism $ {\mathbb {R}} f_*{\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})$. By the adjunction (Proposition 4.18), we have a morphism ${\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathbb {R}} f_!f^!{\mathcal {Y}})\rightarrow {\mathbb{R} \mathcal{H} om}( {\mathbb {R}} f_! {\mathcal {V}}, {\mathcal {Y}})$. We would like to see the composition is an isomorphism. By a local consideration, this can be deduced from the usual case.

Lemma 4.20 Let $\delta \colon X\rightarrow X\times X$ be the diagonal embedding. We have

\[ \delta ^{-1}( {\mathcal {V}}\boxtimes ^{{\mathbb {L}}} {\mathcal {W}})\simeq {\mathcal {V}}\otimes ^{\mathbb{L} } {\mathcal {W}}. \]

Proof. We can apply the same formula for usual sheaves to local representatives. Then we get the desired formula.

As in Lemma 3.17, we can relate $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits$ and usual $\operatorname {Hom}$ as follows. From $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}},{\mathcal {W}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$, we can construct a complex of sheaves $ {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ as in the paragraph before Lemma 3.17.

Lemma 4.21 The space of global sections of ${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}})\otimes \mathbb {k}$ is canonically isomorphic to $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathcal {W}})$.

Proof. Let ${\mathcal {I}}$ be an injective resolution of ${\mathcal {W}}$ and ${\mathcal {F}}$ be a flat resolution of $ {\mathcal {V}}$. Then we have

(4.15)\begin{align} \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{W}})&\cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))}({\mathcal{V}}, {\mathcal{I}})\nonumber\\ &\cong H^0(\operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}_{\Lambda_{({\bar{X}}, D_X)}}}({\mathcal{V}},{\mathcal{I}})(X))\nonumber\\ &\cong H^0(\mathop{{{\mathcal{H}}}om}\nolimits({\mathcal{F}}, {\mathcal{I}})\otimes \mathbb{k}(X)). \end{align}

Actually $\otimes \mathbb {k}$ is exact, as we will see in the proof of Lemma 6.1. This completes the proof.

Lemma 4.22 For a tame morphism $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$, the following hold:

1. (i) $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}\otimes ^{\mathbb {L}}{\mathcal {W}},{\mathcal {X}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, {\mathbb {R}}\mathop {{{\mathcal {H}}}om}\nolimits ({\mathcal {W}},{\mathcal {X}}))$;

2. (ii) $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}(f^{-1}{\mathcal {Y}}, {\mathcal {W}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}( {\mathcal {V}}', {\mathbb {R}} f_* {\mathcal {V}})$;

3. (iii) $\operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)}))}(f_! {\mathcal {V}}, {\mathcal {Y}})\cong \operatorname {Hom}_{D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))}( {\mathcal {V}}, f^!{\mathcal {Y}})$.

Proof. This follows from Lemmas 4.21, 4.10, 4.11, Proposition 4.19.

Lemma 4.23 We have the following:

(4.16)\begin{gather} {\mathbb{R}} f_!({\mathcal{V}}\otimes^{\mathbb{L}} f^{{-}1}{\mathcal{Y}})\simeq {\mathbb{R}} f_!{\mathcal{V}}\otimes^{\mathbb{L}} {\mathcal{Y}}, \end{gather}

(4.17)\begin{gather}f^{!}{\mathbb{R}\mathcal{H} om}({\mathcal{Y}}_1, {\mathcal{Y}}_2)\simeq {\mathbb{R}\mathcal{H} om}(f^{{-}1}{\mathcal{Y}}_1, f^!{\mathcal{Y}}_2), \end{gather}

(4.18)\begin{gather}f^{{-}1}({\mathcal{Y}}_1\otimes^{\mathbb{L}}{\mathcal{Y}}_2)\simeq f^{{-}1}{\mathcal{Y}}_1\otimes^{\mathbb{L}} f^{{-}1}{\mathcal{Y}}_2 . \end{gather}

Proof. The assertions follow easily from Yoneda's Lemma.

We would like to state a useful lemma. Let $U$ be an open subset of $X$ and $\bar {U}$ be the closure inside $\bar {X}$. Consider the map $i\colon (\bar {U}, D_U:=\bar {U}{\backslash } U)\rightarrow {({\bar {X}}, D_X)}$. We denote the closed complement of $U$ in $\bar {X}$ by $V$. We denote the map $j\colon (V, V\cap D_X)\rightarrow {({\bar {X}}, D_X)}$.

Lemma 4.24 There exists an exact triangle in $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$:

(4.19)\begin{equation} i_!i^{{-}1}{\mathcal{V}}\rightarrow {\mathcal{V}}\rightarrow j_*j^*{\mathcal{V}}\xrightarrow{[1]}. \end{equation}

Proof. Note that $i$ and $j$ are tame maps. Again, the statement follows from the corresponding statement for usual sheaves and the commutativity results for $[\cdot ]$ proved early in this subsection.

5. Irregular constructibility

In this section, we introduce the notion of ${\mathbb {C}}$-constructibility for objects in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is defined in the same way for stratifications as in the case of usual constructible sheaves but with a strong assumption on gradings coming from Sabbah, Mochizuki and Kedlaya's Hukuhara–Levelt–Turrittin theorem. In this section, we consider ${({\bar {X}}, D_X)}=(X, \varnothing )$ where $X$ is a complex manifold. We denote $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ by $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.

5.1 Formal structure

In this subsection, we recall as a motivation the theory of formal structures of meromorphic connections initiated by Sabbah [Sab00] and developed by Mochizuki (algebraic case) [Moc11] and Kedlaya (analytic case) [Ked11].

Let $Z$ be a divisor in a complex manifold $X$ and $\hat {\mathcal{O} }_{x}$ be the formal completion of ${\mathcal {O}}_X$ at $x\in X$. Let ${\mathcal {M}}$ be a meromorphic connection over $X$ with poles along $Z$. We set $\hat {{\mathcal {M}}}_x={\mathcal {M}}_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$ and $\hat {\mathcal{O} }(*Z)_x:={\mathcal {O}}(*Z)_x\otimes _{{\mathcal {O}}_x}\hat {\mathcal{O} }_x$.

Definition 5.1

1. (i) For $\phi \in \hat {\mathcal{O} }(*Z)_{x}$, we set $\hat {{\mathcal {E}}}(\phi )$ to be $\hat {\mathcal{O} }(*Z)_{x}$ as a $\hat {\mathcal{O} }_x$-module with a connection $\nabla$ over $\hat {\mathcal{O} }_x$ such that

   (5.1)\begin{equation} \nabla s:=\partial(\phi)\cdot s \end{equation}
   for the generator $s$.

2. (ii) We assume that $Z$ is a normal crossing divisor and take a local coordinate $\{x_i\}_{i=1}^n$ such that $Z$ is defined by $\prod _{i=1}^mx_i=0$. An $\hat {\mathcal{O} }(*Z)$-module $\hat {{\mathcal {R}}}$ with a connection $\nabla$ is regular if there exists an $\hat {\mathcal{O} }_x$-submodule ${\mathcal {L}}$ such that ${\mathcal {L}}\otimes _{\hat {\mathcal{O} }_x}\hat {\mathcal{O} }(*Z)_x\cong \hat {{\mathcal {R}}}$ and $\nabla ({\mathcal {L}})\subset {\bigoplus} _{i=1}^m x^{-1}_i{\mathcal {L}}$.

Definition 5.2 We continue the notation in Definition 5.1(ii).

1. (i) A good decomposition of $\hat {{\mathcal {M}}}_x$ is an isomorphism

   (5.2)\begin{equation} \hat{{\mathcal{M}}}_x\cong \bigoplus_{\alpha\in I}\hat{{\mathcal{E}}}(\phi_\alpha)\otimes_{\hat{\mathcal{O}}(*Z)_x}\hat{\mathcal{R}}_\alpha, \end{equation}
   where $\phi _\alpha \in \hat {\mathcal{O} }(*Z)_{x}$ and each $\hat {\mathcal {R}}_\alpha$ is regular with the following conditions.

   1. (a) Each $\phi _\alpha$ has the form $u\prod _{j=1}^mx_i^{-i_j}$ for some unit $u\in \hat {\mathcal{O} }_x$ and nonnegative integers $i_1,\ldots , i_m$.

   2. (b) For $\alpha , \beta \in I$, if $\phi _a-\phi _\beta \not \in \hat {\mathcal{O} }_x$, then $\phi _\alpha -\phi _\beta$ has the form $u\prod _{j=1}^mx_i^{-i_j}$ for some unit $u\in \hat {\mathcal{O} }_x$ and nonnegative integers $i_1,\ldots , i_m$.

2. (ii) We say ${\mathcal {M}}$ admits a good decomposition at $x\in Z$ if $\hat {{\mathcal {M}}}_x$ admits a good decomposition.

In general, meromorphic connections do not have good decompositions as explained in [Sab00]. Sabbah's conjecture says that they do after modifications, which is proved by Mochizuki and Kedlaya.

Theorem 5.3 [Ked11, Theorem 8.2.2]

For a point $x\in Z$, there exists an open neighborhood $U$ of $z$ and a map $f\colon Y\rightarrow U$ which is a proper modification, and at each point of $f^{-1}(z)$, there exists a local covering $\pi$ ramified at $f^{-1}(Z)$ such that $\pi ^*f^*{\mathcal {E}}$ admits a good decomposition at each point of $y\in \pi ^{-1}f^{-1}(Z)$.

As explained in [Sab11], using Mochizuki's result, we have additional results. For $\hat {{\mathcal {M}}}_x$ which admits a good decomposition, let $\Phi _{x}$ be the subset of $\hat {\mathcal{O} }(*Z)_x/ \hat {\mathcal{O} }_x$ consisting of the classes of $\phi _\alpha$ values.

Theorem 5.4 [Sab11, Theorem 2.2.1]

The subset $\Phi _x$ is actually a subset of ${\mathcal {O}}(*Z)_z/{\mathcal {O}}_x$. Moreover, there exists a neighborhood $U$ of $x$ such that for any $x'\in U$, $\hat {{\mathcal {M}}}_{x'}$ has a good decomposition and $\Phi _{x'}$ is given by the restriction of representatives of $\Phi _x$.

Let $\varpi \colon \tilde {X}(Z)\rightarrow X$ be the real blow-up of $X$ along $Z$ (with real analytic structure specified in [DK16]). Let $C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ be the subsheaf of the sheaf of $C^\infty$-functions consisting of functions which are tempered at the exceptional divisor. Let further ${\mathcal {A}}_{\tilde {X}(Z)}$ be the subsheaf of $C^{\infty ,\mathrm {temp}}_{\tilde {X}}(Z)$ consisting of functions whose restrictions on $X{\backslash } Z$ are holomorphic. We set ${\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}:={\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {O}}_X} {\mathcal {D}}_X$. For a ${\mathcal {D}}$-module ${\mathcal {N}}$ on $X$, we set $\varpi ^*{\mathcal {N}}:={\mathcal {D}}^{\mathcal {A}}_{\tilde {X}(Z)}\otimes _{\varpi ^{-1}{\mathcal {D}}_X}\varpi ^{-1}{\mathcal {N}}$.

Suppose that ${\mathcal {M}}$ has a good decomposition ${\bigoplus} _{\alpha \in I}\hat {\mathcal {E}}(\phi _\alpha )\otimes \hat {\mathcal {R}}_\alpha$ at $x$. For each $\phi _\alpha$, by taking a lift locally around $x$, we set ${\mathcal {E}}(\phi _\alpha )$ to be a meromorphic connection $({\mathcal {O}}(*Z), \nabla )$ defined by $\nabla s:=\partial (\phi ) s$ for the generator $s$. We also set ${\mathcal {R}}_\alpha$ to be a regular meromorphic connection defined locally around $x$ corresponding to $\hat {{\mathcal {R}}}_\alpha$.

The following theorem is proved in [Moc11] and explained in [Sab13].

Theorem 5.5 [Sab13, Theorem 12.5], [Moc11, § 3]

There exists an open covering $\{U_i\}$ of a neighborhood of $\varpi ^{-1}(x)$ such that each restriction $(\varpi ^*{\mathcal {M}})|_{U_i}$ is isomorphic to $(\varpi ^*({\bigoplus} _{\alpha \in I}{\mathcal {E}}(\phi _\alpha )\otimes {\mathcal {R}}_\alpha ))|_{U_i}$.

5.2 Irregular constant sheaf $\Lambda ^\phi$

In this subsection, we prepare some preliminary lemmas concerning a class of modules.

Let ${(\bar {S}, D_S)}$ be a topological space with boundary. Let $\phi$ be a ${\mathbb {C}}$-valued continuous function over $S:=\bar {S}{\backslash } D_S$. We set

(5.3)\begin{equation} \begin{gathered} \operatorname{Gr}^a\Lambda^\phi_S:=p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi},\\ \Lambda^\phi_{S}:=\bigoplus_{a\in {\mathbb{R}}}p_*\Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant{\mathop{\mathfrak{Re}}\nolimits}\phi}, \end{gathered} \end{equation}

where $\mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi }$ is the constant sheaf supported on the set $\{(s, t)\in S\times {\mathbb {R}}\,|\, t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (s)\}$ and $p\colon S\times {\mathbb {R}}\rightarrow S$ is the projection.

Lemma 5.6 The sheaf $\Lambda ^\phi _{S}$ defines an object of $\mathrm {Mod}^ {\mathbb {R}}(\Lambda _S)$. In particular, an object of $\Lambda ^\phi _{(\bar {S}, D_S)}:=[\Lambda ^\phi _S]\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.

Proof. Since the sheaf is globally presented as a direct sum, the restriction morphism preserves grading. The $\Lambda$-action is given as follows. For $b\in \mathbb{R} _{\geqslant 0}$, we have a canonical morphism

(5.4)\begin{equation} \Gamma_{S\times [{-}a,\infty)}\mathbb{k}_{t\geqslant {\mathop{\mathfrak{Re}}\nolimits}\phi}\rightarrow \Gamma_{S\times [{-}a-b,\infty)}\mathbb{k}_{t\geqslant {\mathop{\mathfrak{Re}}\nolimits}\phi}. \end{equation}

This action gives the action of $T^b$.

We would like to understand the structure of $\Lambda ^\phi _S$.

Lemma 5.7 Let $U$ be a connected open subset of $S$ such that $\phi |_U$ is bounded. Set $b:=\inf _U {\mathop {\mathfrak {Re}}\nolimits } \phi$. Then $\Lambda ^\phi _S(U)\cong \Lambda \cdot T^b$.

Proof. Note that $\operatorname {Gr}^a\Lambda ^\phi _S(U)\cong \Gamma _{U\times [-a, \infty )}(U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. This is the kernel of the restriction morphism $\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\rightarrow \Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })$. Since $U$ is connected, the set defined by $t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi$ is also connected. Hence we have $\Gamma (U\times {\mathbb {R}}, \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong \mathbb {k}$. On the other hand, $\Gamma (U\times (-\infty , -a), \mathbb {k}_{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi })\cong 0$ if and only if $U\times (-\infty , -a)\cap \{t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi \}=\varnothing$. This is equivalent to $-a<\inf _U {\mathop {\mathfrak {Re}}\nolimits }\phi$. This completes the proof.

For given $x\in S$, let us set

(5.5)\begin{equation} \Lambda^{\phi(x)}:=\begin{cases} \mathop{{\displaystyle\bigoplus}}\limits_{{-}a\leqslant {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{if $x$ is a local minimum},\\ \mathop{{\displaystyle\bigoplus}}\limits_{{-}a< {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}\mathbb{k} & \text{otherwise}. \end{cases} \end{equation}

These are $ {\mathbb {R}}$-graded $\Lambda$-modules with obvious gradings. Note that these are torsion-free $\Lambda$-modules and the ring $\Lambda$ has a valuation. Hence these modules are flat.

From this lemma, the following is clear.

Corollary 5.8 For $x\in S$, the stalk $(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$.

Corollary 5.9 We have $\operatorname {Gr}^d\Lambda ^\phi _S\cong \mathbb {k}_{\mathrm {Int}\overline {\{ x| -d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$.

Proof. Let $x$ be a point with $ {\mathop {\mathfrak {Re}}\nolimits }\phi (x)=-d$. The point $x$ is a local minimum if and only if $x$ is in the interior of the closure of $\{-x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}$. This completes the proof.

Also, the module $\Lambda ^\phi _{(\bar {S}, D_S)}$ plays the role similar to the constant sheaves in the usual theory of sheaves. The following lemma explains this similarity.

Lemma 5.10 The module $\Lambda ^\phi _{(\bar {S}, D_S)}$ is a flat object in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{{(\bar {S}, D_S)}})$.

Proof. Let $ {\mathcal {V}}\rightarrow {\mathcal {W}}$ be an injective morphism in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We would like to show the induced morphism $ {\mathcal {V}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}\rightarrow {\mathcal {W}}\otimes \Lambda ^\phi _{(\bar {S}, D_S)}$ is again injective. There exists a covering $\{U_i\}$ of $S$ which is locally finite in $\bar {S}$ such that there exist lifts $ {\mathcal {V}}_i, {\mathcal {W}}_i$ of $ {\mathcal {V}}$ and ${\mathcal {W}}$ over each $U_i$. It is enough to prove the injectivity over each $U_i$.

By Lemma 2.14, one can assume the restriction $ {\mathcal {V}}_i\rightarrow {\mathcal {W}}_i$ is still injective. Since the tensor product commutes with taking stalks, it reduces to show that $ {\mathcal {V}}_x\otimes (\Lambda ^\phi _S)_x\rightarrow {\mathcal {W}}_x\otimes (\Lambda ^\phi _S)_x$ is injective. Since $(\Lambda ^\phi _S)_x\cong \Lambda ^{\phi (x)}$ (Corollary 5.8) is a torsion-free $\Lambda$-module, this completes the proof.

Lemma 5.11 Let $\phi _1$ and $\phi _2$ be ${\mathbb {C}}$-valued continuous functions over connected $S$ such that $ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded from above. Then there exists a canonical identification

(5.6)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)})}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)})\cong \mathbb{k}. \end{equation}

If moreover $ {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2$ is bounded, the two objects are isomorphic.

Proof. Since $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _1- {\mathop {\mathfrak {Re}}\nolimits }\phi _2\}$ is bounded, there exists a large $c\in {\mathbb {R}}$ such that $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1$. The nonzero map $\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t}\rightarrow \mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits }\phi _{2}+c\geqslant t}$ coming from the inclusion $\{ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c\geqslant t\}\subset \{ {\mathop {\mathfrak {Re}}\nolimits }\phi _1\geqslant t\}$ induces a morphism $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S\langle c\rangle $ of $ {\mathbb {R}}$-graded $\Lambda _S$-modules. If $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1\}$ is also bounded, in the same way, we also have a morphism $\Lambda ^{\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\langle d\rangle $ for some $d\geqslant 0$. The composition $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _1}_S\langle c+d\rangle $ is given by $T^{c+d}$. This is the identity of $\Lambda ^\phi _{(\bar {S}, D_S)}$ in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. The same for the other direction. This completes the proof of the second part of the statement. We call morphism $\Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2}_S$ of this kind as well as their scalar multiples standard morphisms. In the below, we will see there are only standard morphisms.

Let $f$ be a nonzero morphism in $\operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})$. Let us take a lift $\tilde {f}\colon \Lambda ^{\phi _1}_S\rightarrow \Lambda ^{\phi _2+c}_S$ as a morphism of $ {\mathbb {R}}$-graded $\Lambda$-modules locally on $U\subset S$. We can take $c$ such that $c+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2> {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ and replace $\phi _2$ with $\phi _2+c$ We consider $d\in {\mathbb {R}}$ such that the grading $d$-part of $\tilde {f}$ is nonzero. To see this part more explicitly, let us prepare some notation.

Let us set $\mathrm {Int}\overline {\{ x\in U\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}=\sqcup _a S_{d,i}^a$ to be the decomposition into connected components. Since $\operatorname {Gr}^d\Lambda _U^\phi =\mathbb {k}_{\mathrm {Int}\overline {\{ x|-d< {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}}$, we have $\operatorname {Gr}^d\Lambda _U^{\phi _i}={\bigoplus} _{a}\mathbb {k}_{S^a_{d,i}}$. We have

(5.7)\begin{equation} \tilde{f}_d\colon \bigoplus_{a}\mathbb{k}_{S^a_{d,1}} \rightarrow \bigoplus_{a}\mathbb{k}_{S^a_{d,2}}. \end{equation}

There exists $d'\in \mathbb{R} _{\geqslant 0}$ such that there exists a connected component $S_i$ of $\mathrm {Int}\overline {\{ x\,|\,-d'< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$ for each $i$ such that $S_i\supset \mathrm {Int}\overline {\{ x\,|\,-d< {\mathop {\mathfrak {Re}}\nolimits }\phi _i(x)\}}$. Then we have a commutative diagram.

(5.8)

Since $S_1$ and $S_2$ are connected, the hom-space between them is one-dimensional. Hence $\tilde {f}_d$ is induced by a standard morphism. This completes the proof.

We prepare the following crucial lemma. The corresponding observation in the theory of enhanced ind-sheaves is a key to the formulation of irregular Riemann–Hilbert correspondence [DK16].

Lemma 5.12 Let ${(\bar {S}, D_S)}$ be a topological space with boundary with $S$ connected. Let $\phi _1, \phi _2$ be ${\mathbb {C}}$-valued continuous functions on $S$. Assume that there exists an open subset $V$ of $S$ such that $\bar {V}\cap D_S$ is nonempty and $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is divergent to $-\infty$ on $\bar {V}\cap D_S$. Then there exists no nonzero morphisms from $\Lambda _{(\bar {S}, D_S)}^{\phi _1}$ to $\Lambda _{(\bar {S}, D_S)}^{\phi _2}$.

Proof. For $f\in \operatorname {Hom}_{\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})}(\Lambda _{(\bar {S}, D_S)}^{\phi _1}, \Lambda _{(\bar {S}, D_S)}^{\phi _2})$, let us take a lift $\tilde {f}\colon \Lambda _{(\bar {S}, D_S)}^{\phi _1}\rightarrow \Lambda _{(\bar {S}, D_S)}^{\phi _2+c}$ as a morphism between $ {\mathbb {R}}$-graded $\Lambda _S$-modules. Since $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negatively divergent, there exists a neighborhood $U$ of $D_S$ such that $ {\mathop {\mathfrak {Re}}\nolimits }\phi _2+c- {\mathop {\mathfrak {Re}}\nolimits }\phi _1$ is negative on $U{\backslash } D_S$. Hence over $U{\backslash } D_S$, the restriction of $\tilde {f}$ is zero there. By Lemma 5.11 and the connectedness of $S$, $f$ is zero everywhere.

We also give the following.

Lemma 5.13 For $\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ $(i=1,2)$, we have $\Lambda ^{\phi _1}_{(\bar {S}, D_S)}\otimes \Lambda ^{\phi _2}_{(\bar {S}, D_S)}\cong \Lambda ^{\phi _1+\phi _2}_{(\bar {S}, D_S)}$. In particular, $\Lambda ^\phi _{(\bar {S}, D_S)}\otimes \Lambda ^{-\phi }_{(\bar {S}, D_S)}\cong \Lambda _{(\bar {S}, D_S)}$.

Proof. We have $\operatorname {Gr}^a\Lambda _S^{\phi _i}=\mathbb {k}_{\{ x| {\mathop {\mathfrak {Re}}\nolimits }\phi (x)>-a\}}$ for $i=1,2$. Hence we have a map $\operatorname {Gr}^a\Lambda ^{\phi _1+\phi _2}_S\rightarrow \operatorname {Gr}^b\Lambda ^{\phi _1}_S\otimes _k\operatorname {Gr}^c\Lambda ^{\phi _2}_S$ for $a=b+c$. Hence we get a map $m\colon \Lambda ^{\phi _1+\phi _2}_S\rightarrow \Lambda ^{\phi _1}_S\otimes \Lambda ^{\phi _2}_S$. By Corollary 5.8, the stalks of both sides at $x\in X$ are ${\bigoplus} _{-a\leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$ or ${\bigoplus} _{-a< {\mathop {\mathfrak {Re}}\nolimits }\phi _1(x)+ {\mathop {\mathfrak {Re}}\nolimits }\phi _2(x)}\Lambda ^{\phi _1(x)+\phi _2(x)}_S$. Hence the kernel and cokernel of $m$ vanishes by multiplying $T^a$ for any $a\in {\mathbb {R}}_{>0}$. Therefore the kernel and cokernel are zero in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. This completes the proof.

Similarly, we have

Lemma 5.14 For $\Lambda ^{\phi _i}_{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ $(i=1,2)$, we have

\[ \mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})\cong \Lambda ^{\phi _2-\phi _1}_{(\bar {S}, D_S)}. \]

Proof. One can prove in a similar way as in the proof of Lemma 5.13.

The following will be repeatedly used later.

Corollary 5.15 We have ${\mathbb{R} \mathcal{H} om}(\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \Lambda ^{\phi _2}_{(\bar {S}, D_S)})\simeq \Lambda ^{\phi _2-\phi _1}_{(\bar {S}, D_S)}$.

Proof. Let ${\mathcal {I}}$ be an injective resolution of $\Lambda ^{\phi _2}_{(\bar {S}, D_S)}$. We have the following:

(5.9)\begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\mathcal{V}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}\otimes \Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{C(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\mathop{{{\mathcal{H}}}om}\nolimits(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, {\mathcal{I}})). \end{align}

Here we used flatness of $\Lambda ^{\phi _1}_{(\bar {S}, D_S)}$.

First, note that $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})\cong \Lambda ^{-\phi _1}_{(\bar {S}, D_S)}\otimes {\mathcal {I}}$ in $C(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)}))$. Second, ${\mathcal {I}}$ is locally given by $[\prod _x {\mathcal {F}}_x]$ where ${\mathcal {F}}_x$ is a skyscraper sheaf. Since $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, \prod _x{\mathcal {F}}_x)\cong \prod _x\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {F}}_x)$, the object $\mathop {{{\mathcal {H}}}om}\nolimits (\Lambda ^{\phi _1}_{(\bar {S}, D_S)}, {\mathcal {I}})$ is also injective. Hence we have

(5.10)\begin{align} &\operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}}, {\mathbb{R}\mathcal{H} om}(\Lambda^{\phi_1}_{(\bar{S}, D_S)}, \Lambda^{\phi_2}_{(\bar{S}, D_S)}))\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}{\mathcal{I}})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{-\phi_1}_{(\bar{S}, D_S)}\otimes^{\mathbb{L}}\Lambda^{\phi_2}_{(\bar{S}, D_S)})\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}({\mathcal{V}},\Lambda^{\phi_2-\phi_1}_{(\bar{S}, D_S)}). \end{align}

This completes the proof.

5.3 Irregular local systems

Let $V$ be a neighborhood of $0\in {\mathbb {C}}^n$ and consider a simple normal crossing $D_I={\bigcup} _{i\in I}\{z_i=0\}\cap V$. For $A:=\{a_i\}\in {\mathbb {Z}}^{I}$, $\Phi _A\colon {\mathbb {C}}^n\rightarrow {\mathbb {C}}^n$ is defined by $(z_1^{a_1},\ldots , z_n^{a_n})$ where $a_i=0$ for $i\not \in I$.

Definition 5.16

1. (i) A correspondence $f\colon V{\backslash } D_I\rightarrow {\mathbb {C}}$ is a multi-valued meromorphic function if there exists $A:=\{a_i\}\in {\mathbb {Z}}^{I}$ and a meromorphic function $f'$ on $\Phi _A^{-1}(V)$ with poles in $\Phi _A^{-1}(D_I)$ such that $f$ is equal to $z\mapsto \{ f'(z') \,|\, z'\in (\Phi _A)^{-1}(z)\}$.

2. (ii) A finite set of multi-valued meromorphic function is said to be good, if it satisfies the conditions in Definition 5.2 after taking the pull-backs along $\Phi _A$.

For a multi-valued meromorphic function $\phi$ and an open subset $U$ on which $\phi$ is represented by a set of single-valued holomorphic functions $\{\phi _k\}_{k\in K}$, we set $\Lambda ^\phi :={\bigoplus} _{k\in K}\Lambda ^{\phi _k}$.

For $S$ a locally closed complex submanifold $X$, consider $(\bar {S}, D_S:=\bar {S}{\backslash } S)$ as a topological space with boundary.

Definition 5.17 Let $ {\mathcal {V}}$ be an object of $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$. We call $ {\mathcal {V}}$ a good irregular local system if the following hold.

1. (i) The boundary $D_S$ is normal crossing.

2. (ii) For any point $x\in D_S$, there exists a neighborhood $U$ of $x$ such that the restriction $ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf $\Lambda _U$.

3. (iii) For any point $x\in \bar {S}{\backslash } S$, there exist:

   1. (a) a neighborhood $U$ of $x$;

   2. (b) a finite good set of multi-valued meromorphic functions $\{\phi _j\}_{j\in J}$ over $U$ with poles in $D_S$; and

   3. (c) a finite cover $\{U_k\}_{k\in K}$ of $U{\backslash } U\cap D_S$

   such that we have both the following.

   1. • There exists an open covering $\{U_k'\}_{k\in K}$ of the real blow-up of $U$ along $D_S$ (in the sense of [DK16]) with $U_k=U_k'\cap (U{\backslash } D_S)$.

   2. • Each restriction of $ {\mathcal {V}}|_{U_k}:= {\mathcal {V}}|_{(\overline {U_k}, \overline {U_k}\cap D_S)}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}^{-1} {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D_S)})$ is isomorphic to the finite direct sum ${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D_S)}$. Here $\overline {U_k}$ means $U_k\cup (D_S\cap \overline {U_k})$ and $\iota _{(\overline {U_k}, \overline {U_k}\cap D_S)}$ is the canonical map induced by the inclusion $\overline {U_k}\hookrightarrow \bar {S}$.

If the set of multi-valued functions is actually the set of meromorphic functions, we call it a unramified good irregular local system.

Lemma 5.18 Definition 5.17(iii) is equivalent to the following. For any point $x\in \bar {S}{\backslash } S$, there exist:

1. (a) a neighborhood $U$ of $x=:0$ (with the notation used in Definition 5.16);

2. (b) $A:=\{a_i\}\in {\mathbb {Z}}^{I}$;

3. (c) a finite set of meromorphic functions $\{\phi _j\}_{j\in J}$ over $U':=\Phi _A^{-1}(U)$ with poles in $D':=\Phi _A^{-1}(D_I)$; and

4. (d) a finite cover $\{U_k\}_{k\in K}$ of $U'{\backslash } U'\cap D'$

such that we have both the following.

1. • There exists an open covering $\{U_k'\}_{k\in K}$ of the real blow-up of $U$ along $D'$ with $U_k=U_k'\cap (U{\backslash } D')$.

2. • Each restriction of $(\Phi _A^* {\mathcal {V}})|_{(\overline {U_k}, \overline {U_k}\cap D')}:=\iota _{(\overline {U_k}, \overline {U_k}\cap D')}^{-1}(\Phi _A^* {\mathcal {V}})\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\overline {U_k}, \overline {U_k}\cap D')})$ is isomorphic to the finite direct sum ${\bigoplus} _{j\in J}\Lambda ^{\phi _j}_{(\overline {U_k}, \overline {U_k}\cap D')}$. Here $\iota _{(\overline {U_k}, \overline {U_k}\cap D')}$ is the canonical map induced by the inclusion $\overline {U_k}\hookrightarrow \bar {S}$.

Proof. This is just from the definition of multi-valued meromorphic functions.

Definition 5.19 For a complex manifold $U$ with a divisor $D$, a modification of $(U, D)$ is a morphism $f\colon ({U'}, D')\rightarrow (U, D)$ where $({U'}, D')$ is another complex manifold with a divisor and $f$ is a projective map between ${U'}$ and $U$ preserving divisors and induces the identity map between $U{\backslash } D$ and ${U'}{\backslash } D'$.

Definition 5.20 An object $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ is said to be an irregular local system if the following hold.

1. (i) For any point $x\in S$, there exists a neighborhood $U$ of $x$ such that the restriction $ {\mathcal {V}}|_U\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(U, \varnothing )})$ is isomorphic to a finite direct sum of the constant sheaf $\Lambda _U$.

2. (ii) For any point $x\in D_S$, there exists a neighborhood $U$ of $x$ and a modification $p\colon (U',D') \rightarrow ({U}, D_S\cap U)$ such that $p^{-1}( {\mathcal {V}}|_{(U,D_S\cap U)})$ is a good irregular local system.

Let $ {\mathcal {V}}$ be an irregular local system on ${(\bar {S}, D_S)}$. Take a point $x\in D_S$. Then by the definition of irregular local systems, there exists a relatively compact open neighborhood $U$ of $x$ with a modification $p\colon U'\rightarrow U$ such that for any $y\in p^{-1}(D_S)=:D'$, there exists a finite cover $\{U_k\}_k$ of $U'{\backslash } D'$ given in the definition of good irregular local systems. We have $ {\mathcal {V}}|_{U_k}\cong {\bigoplus} _i\Lambda ^{\phi _i}_{(\overline {U_k}, \overline {U_k}\cap D')}$.

Since $U'{\backslash } D'\cong U{\backslash } D_S$. we get a finite covering ${\mathcal {U}}$ of $U{\backslash } D_S$ such that $ {\mathcal {V}}|_{{\bar {U}}, D_S\cap {\bar {U}}}$ is isomorphic to a direct sum of irregular constant sheaves for each $U\in {\mathcal {U}}$.

Definition 5.21 We call a finite covering ${\mathcal {U}}$ of $U{\backslash } D_S$ given above a sectorial covering for $ {\mathcal {V}}$ around $x$.

Lemma 5.22 For $ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$ and $x\in D_S$, there exists a neighborhood $U$ of $x$ with a modification $(U',D')\rightarrow (U, D)$ such that $p^{-1}( {\mathcal {V}}|_{(U, U\cap D_S)})$ and $p^{-1}({\mathcal {W}}|_{(U, U\cap D_S)})$ are irregular local systems. In particular, $ {\mathcal {V}}$ and ${\mathcal {W}}$ have a common sectorial covering.

Proof. This is standard.

Next we would like to define one of the fundamental objects in this paper.

Definition 5.23 Let $ {\mathcal {V}}$ be an object of $\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)$. We say $ {\mathcal {V}}$ is irregular constructible if the following hold. There exists a ${\mathbb {C}}$-analytic stratification ${\mathcal {S}}$ of $X$ such that the restriction $ {\mathcal {V}}|_{(\bar {S}, D_S:=\bar {S}{\backslash } S)}$ to each stratum $S\in {\mathcal {S}}$ is an irregular local system as an object of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{(\bar {S}, D_S)})$.

It is clear that the definition remains valid after refining the stratification. Let us denote the full subcategory of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ spanned by irregular constructible sheaves by $\mathrm {Mod}_{ic}(\Lambda _X)$.

Proposition 5.24 The category $\mathrm {Mod}_{ic}({\Lambda _X})$ is abelian.

Remark 5.25 This statement is a little bit interesting since the category of filtered vectors spaces is not abelian (see Remark 2.4).

Proof Proof of Proposition 5.24

Since $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ is abelian, it suffices to show kernels, cokernels, images, and coimages of morphisms between irregular constructible sheaves are also irregular constructible sheaves. Let $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism between irregular constructible sheaves. One can take a common ${\mathbb {C}}$-Whitney stratification for $ {\mathcal {V}}$ and ${\mathcal {W}}$. Then it suffices to show Lemma 5.26 below.

Lemma 5.26 Kernels, cokernels, images, coimages of morphisms between irregular local systems are irregular local systems.

To prove Lemma 5.26, we prepare some notions and lemmas.

Definition 5.27 Let $\phi _i$ ($i=1,2$) be meromorphic functions over $U$ with poles in $D$. We say $\phi _1$ and $\phi _2$ are equivalent if there exists a bounded holomorphic function $\phi$ over $U$ such that $\phi _1=\phi _2+\phi$. We denote the set of meromorphic functions over $(U, D)$ modulo this equivalence relation by $\mathrm {M}(U,D)$.

Recall that $\Lambda ^{\phi _1}_{(U,D)}$ and $\Lambda ^{\phi _2}_{(U, D)}$ are canonically isomorphic for $\phi _1=\phi _2\in M(U, D)$ by Lemma 5.11.

Proof Proof of Lemma 5.26

Let $ {\mathcal {V}}$ and ${\mathcal {W}}$ be irregular local systems over $(U,D)$. Since the definition of irregular local systems is local, we can consider locally on a open subset $U$. There exists a modification $p\colon (U', D')\rightarrow (U, D)$ such that $p^{-1} {\mathcal {V}}$ and $p^{-1}{\mathcal {W}}$ are both good irregular local systems by Lemma 5.22.

A morphism $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ induces a morphism over $U$ and we pull-back $f$ by $p$. Then by the exactness of the pull-back, kernel cokernel, image, coimage (we denote those by $A$) of $p^{-1}f$ are pull-backs of those for $f$ i.e. $p^{-1}A(f)\cong A(p^{-1}f)$.

Furthermore, we can pull-back more by a covering map $\Phi _A$ to make $p^{-1} {\mathcal {V}}$ and $p^{-1}{\mathcal {W}}$ unramified irregular local systems. Then again, $\Phi _A^{-1}p^{-1}A(f)\cong A(\Phi _A^{-1}\circ p^{-1}f)$. It suffices to show that this is an irregular local system.

So we reset the notation. Let $ {\mathcal {V}}$ and ${\mathcal {W}}$ be unramified good irregular local systems and $f\colon {\mathcal {V}}\rightarrow {\mathcal {W}}$ be a morphism. Then there exist sets of meromorphic functions $\Phi _ {\mathcal {V}}$ and $\Phi _{\mathcal {W}}$ over $(U, D)$ which are appeared in the definition of irregular local system.

Take a point $x\in D$, a neighborhood $U$ of $x$, and a sectorial covering ${\mathcal {U}}$ of $U{\backslash } D$ for $ {\mathcal {V}}$ and ${\mathcal {W}}$. On each $U\in {\mathcal {U}}$, we have isomorphisms $ {\mathcal {V}}|_U\cong {\bigoplus} _{\phi \in \Phi _ {\mathcal {V}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi$ and ${\mathcal {W}}|_U\cong {\bigoplus} _{\psi \in \Phi _{\mathcal {W}}}\Lambda _{(\bar {U}, \bar {U}\cap D)}^\psi$.

Suppose the following: there exists a sector $U\in {\mathcal {U}}$ such that the restriction of $f$ to the component $\Lambda ^{\phi }_{(\bar {U}, \bar {U}\cap D)}\rightarrow \Lambda ^\psi _{(\bar {U}, \bar {U}\cap D)}$ is nonzero where $\phi \in \Phi _ {\mathcal {V}}, \psi \in \Phi _{\mathcal {W}}$ with $\phi \neq \psi$.

Let $U'$ be the adjacent sector of $U$. Then the restriction of $f$ to $\Lambda ^{\phi }_{(\overline {U'}, \overline {U'}\cap D)}\rightarrow \Lambda ^\psi _{(\overline {U'}, \overline {U'}\cap D)}$ is nonzero again. This implies $\max \{ {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\psi \}$ is bounded by Lemma 5.11. We can continue this procedure and we eventually will arrive at a sector on which $\phi -\psi$ is negatively divergent since $\phi \neq \psi$. This contradicts the supposition.

Hence we cannot have such a morphism. This means $f|_{U}$ is diagonal with respect to indices $M(U, D)\times M(U,D)$. Hence the morphism $f|_{U}$ is represented by a sum of $c\cdot T^a\colon \Lambda _{(\bar {U}, \bar {U}\cap D)}^\phi \rightarrow \Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$ where $c\in k$ by Lemma 5.11. The $A(c\cdot T^a)$ ia again of the form of a sum of $\Lambda ^\phi _{(\bar {U}, \bar {U}\cap D)}$. This completes the proof.

We prepare the following lemma for the next subsection.

Lemma 5.28 The category $\mathrm {Mod}_{ic}(\Lambda _X)$ is a thick subcategory of $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$.

Proof. Let

(5.11)\begin{equation} 0\rightarrow {\mathcal{V}}\rightarrow {\mathcal{X}}\rightarrow {\mathcal{W}}\rightarrow 0 \end{equation}

be an exact sequence in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$ with $ {\mathcal {V}}, {\mathcal {W}}\in \mathrm {Mod}_{ic}(\Lambda _X)$. Let ${\mathcal {S}}$ be a common stratification of $ {\mathcal {V}}$ and ${\mathcal {W}}$. Since pull-backs are exact, we can reduce to the case that $ {\mathcal {V}}, {\mathcal {W}}$ are irregular local systems on $(\bar {S}, D_S)$. For any point $x\in D_S$, there exists a neighborhood $U$ of $x$ such that $U{\backslash } D_S$ has a finite sectorial covering $\{U_i\}$ and $ {\mathcal {V}}$ (respectively ${\mathcal {W}}$) is isomorphic to ${\bigoplus} _j\Lambda ^{\phi _j}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$ (respectively ${\bigoplus} _{k}\Lambda ^{\psi _k}_{(\overline {U_i}, \overline {U_i}\cap D_S)}$). Hence we have an exact sequence

(5.12)\begin{equation} 0\rightarrow \bigoplus_{j}\Lambda^{\phi_j}_{(\overline{U_i}, \overline{U_i}\cap D_S)}\rightarrow {\mathcal{X}}|_{U_i}\rightarrow \bigoplus_{k}\Lambda^{\psi_k}_{(\overline{U_i}, \overline{U_i}\cap D_S)}\rightarrow 0 \end{equation}

on each $U_i$.

We have already seen that ${\mathbb{R} \mathcal{H} om}(\Lambda ^\psi _{(\overline {U_i}, \overline {U_i}\cap D_S)}, \Lambda ^\phi _{(\overline {U_i}, \overline {U_i}\cap D_S)})\simeq \Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}^{\phi -\psi }$ in Corollary 5.15. Then

(5.13)\begin{align} &\operatorname{Ext}^1_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi)\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\psi, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^\phi[1])\nonumber\\ &\quad \cong \operatorname{Hom}_{D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{(\bar{S}, D_S)}))}(\Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}, \Lambda_{(\overline{U_i}, \overline{U_i}\cap D_S)}^{\phi-\psi}[1])\nonumber\\ &\quad \cong 0, \end{align}

since $\Lambda _{(\overline {U_i}, \overline {U_i}\cap D_S)}$ is free. This completes the proof.

5.4 Derived category and six operations

Definition 5.29 A cohomologically irregular constructible $\Lambda _{({\bar {X}}, D_X)}$-module is an object of $D^b(\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ such that all the cohomologies are irregular constructible sheaves. We denote the full subcategory spanned by those objects by $D^b_{ic}(\Lambda _X)$.

Proposition 5.30 The category $D^b_{ic}(\Lambda _X)$ is a triangulated category.

Proof. This is a standard consequence of the thickness (Lemma 5.28).

We will now see Grothendieck six operations on this category. In the rest of subsection, $ {\mathcal {V}}, {\mathcal {W}}$ will be always objects of $D^b_{ic}(\Lambda _X)$.

Proposition 5.31 We have $ {\mathcal {V}}\otimes ^{\mathbb{L} } {\mathcal {W}}\in D^b_{ic}(\Lambda _X)$.

Proof. This is obvious from (4.18) and Lemma 5.13.

Lemma 5.32 For an irregular constructible sheaf ${\mathcal {X}}$ on $(\bar {U}, D_U)$ (respectively $(V, V\cap D_S)$), $i_!{\mathcal {X}}$ (respectively $j_*{\mathcal {X}}$) is irregular constructible.

Proof. By considering a stratification compatible with $U$ (respectively $V$) and a stratification of ${\mathcal {X}}$, the constructibility of ${\mathcal {X}}$ implies the statement.

For the constant map $a_X\colon X\rightarrow *$, we set $\omega _X^\Lambda :=a_X^!\Lambda \cong \Lambda \otimes _\mathbb {k} \omega _X\in D^b_{ic}(\Lambda _X)$ as usual. We also set

(5.14)\begin{equation} {\mathbb{D}}{\mathcal{V}}:={\mathbb{R}\mathcal{H} om}({\mathcal{V}}, \omega^\Lambda_X)\in D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)). \end{equation}

First note the following.

Lemma 5.33 We have ${\mathbb {D}}\Lambda ^\phi _X\cong \Lambda ^{-\phi }_X\otimes _\mathbb {k}\omega _X$.

Proof. This is a special case of Corollary 5.15.

Then we have the following.

Lemma 5.34 We have ${\mathbb {D}} {\mathcal {V}}\in D^b_{ic}(\Lambda _{X})$.

Proof. Let ${\mathcal {S}}$ be a stratification of $ {\mathcal {V}}$. Let $U$ be the union of open subsets of ${\mathcal {S}}$. By applying Lemma 4.24, we have an exact triangle

(5.15)\begin{equation} {\mathbb{R}\mathcal{H} om}(i_!i^!{\mathcal{V}}, \omega_X^\Lambda)\leftarrow {\mathbb{R}\mathcal{H} om}({\mathcal{V}}, \omega_X^\Lambda)\leftarrow {\mathbb{R}\mathcal{H} om}(j_!j^{{-}1}{\mathcal{V}}, \omega_X^\Lambda)\leftarrow . \end{equation}

Then we have

(5.16)\begin{equation} \begin{gathered} {\mathbb{R}\mathcal{H} om}(i_!i^!{\mathcal{V}}, \omega^\Lambda_X)\simeq i_!{\mathbb{R}\mathcal{H} om}(i^{{-}1}{\mathcal{V}}, i^{{-}1}\omega^\Lambda_X),\\ {\mathbb{R}\mathcal{H} om}(j_!j^{{-}1}{\mathcal{V}}, \omega^\Lambda_X)\simeq j_*{\mathbb{R}\mathcal{H} om}(j^{{-}1}{\mathcal{V}}, j^!\omega^\Lambda_X). \end{gathered} \end{equation}

By Lemma 5.32, we can prove the desired result by induction of the dimension of the strata and Lemma 5.33.

Lemma 5.35 The canonical morphism $ {\mathcal {V}}\rightarrow {\mathbb {D}}{\mathbb {D}} {\mathcal {V}}$ is an isomorphism.

Proof. It is also enough to show the statement for irregular local systems. Then the statement is clear from ${\mathbb {D}}{\mathbb {D}}\Lambda _X^\phi =\Lambda _X^{\phi }$.

Lemma 5.36 We have

(5.17)\begin{equation} \operatorname{Hom}_{D^b_{ic}(\Lambda_X)}({\mathcal{V}}, {\mathcal{W}})\cong \operatorname{Hom}_{D^b_{ic}(\Lambda_X)}({\mathbb{D}}{\mathcal{W}}, {\mathbb{D}}{\mathcal{V}}). \end{equation}

Proof. This is easy and the proof is left to the reader.

Corollary 5.37 The contravariant functor ${\mathbb {D}}\colon D^b_{ic}(\Lambda _X)\rightarrow D^b_{ic}(\Lambda _X)$ is a contravariant equivalence.

Proof. The fully faithfulness of ${\mathbb {D}}$ is Lemma 5.36 and the essential surjectivity is Lemma 5.35.

Proposition 5.38 We have a natural isomorphism

(5.18)\begin{equation} f^!\circ {\mathbb{D}}\cong {\mathbb{D}}\circ f^{{-}1}. \end{equation}

Proof. This is easy and the proof is left to the reader.

Proposition 5.39 We have ${\mathbb{R} \mathcal{H} om}( {\mathcal {V}}, {\mathcal {W}}), f^{-1} {\mathcal {V}}, f^! {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.

Proof. This is easy and the proof is left to the reader.

Let $i_{{({\bar {X}}, D_X)}}\colon {({\bar {X}}, D_X)}\rightarrow (X, \varnothing )$ be the canonical morphism.

Lemma 5.40 The functor $i_{{({\bar {X}}, D_X)}!}\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{\bar {X}})$ is fully faithful embedding onto the full subcategory spanned by objects satisfying $i_{D_X}^{-1} {\mathcal {V}}\simeq 0$. The functor $i_{{({\bar {X}}, D_X)}*}$ is also fully faithful. In both cases, the left quasi-inverses are given by $i_{({\bar {X}}, D_X)}^{-1}$.

Proof. This simply follows from Lemma 4.24

6. Forgetting grading

In this section, we discuss the relationship between irregular constructible sheaves and constructible sheaves. For a topological space with boundary ${({\bar {X}}, D_X)}$, we set $X:={\bar {X}}{\backslash } D_X$.

6.1 Forgetting grading

Lemma 6.1 There exists an exact functor

(6.1)\begin{equation} \mathfrak{F}\colon\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)})\rightarrow \mathrm{Mod}(\mathbb{k}_X) \end{equation}

satisfying the following. For an object $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{{({\bar {X}}, D_X)}})$, take a local lift $\tilde {\mathcal{V} }$ on an open subset $U\subset X$. Let $\tilde {\mathcal{V} }_{0}$ be the underlying ungraded $\Lambda$-module of $\tilde {\mathcal{V} }$. Then $ {\mathfrak {F}}( {\mathcal {V}})|_U\cong \tilde {\mathcal{V} }_0|_U\otimes _\Lambda \mathbb {k}$.

Proof. For an object $ {\mathcal {V}}$, let us take a locally finite covering $\{U_i\}$ of $X$ with lifts $\{\tilde {\mathcal{V} }_i\}\subset \mathrm {Mod}^{\mathfrak {I}}_{pre} (\Lambda _X)$. There exists an isomorphism $f_{ij}\colon [\tilde {\mathcal{V} }_i]|_{U_i\cap U_j}\xrightarrow {\cong } [\tilde {\mathcal{V} }_j]|_{U_i\cap U_j}$ in ${\mathrm {Mod}^{\mathfrak {I}}_{ps}}_{({\bar {X}}, D_X)}(U_{ij})$. We can take a covering $\{U_{ijk}\}$ on which we have a descent data $f_{ijk}\colon [\tilde {\mathcal{V} }_i]|_{U_{ijk}}\rightarrow [\tilde {\mathcal{V} }_j]|_{U_{ijk}}$ for $f_{ij}$ in $\mathrm {Mod}^{\mathfrak {I}}_{pre}(U_{ij})$. Let $\tilde {f}_{ijk}\colon \tilde {\mathcal{V} }_i|_{U_{ijk}}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ijk}}\langle a\rangle $ be a lift of $f_{ijk}$.

Then $f_{ijk}|_{U_{ijk}\cap U_{ijl}}=f_{ijl}|_{U_{ijk}\cap U_{ijl}}$ means there exists $b\in {\mathbb {R}}_{>0}$ such that $T^b\cdot ((\tilde {f}_{ijk}-\tilde {f}_{ijl})|_{U_{ijk}\cap U_{ijl}})=0$. This means $\tilde {f}_{ijk}\otimes _\Lambda \mathbb {k} =\tilde {f}_{ijl}\otimes _\Lambda \mathbb {k}$. Hence the set $\{\tilde {f}_{ijk}\}$ gives an isomorphism $f_{ij}\otimes _\Lambda \mathbb {k}\colon \tilde {\mathcal{V} }_i|_{U_{ij}}\otimes _\Lambda \mathbb {k}\rightarrow \tilde {\mathcal{V} }_j|_{U_{ij}}\otimes _\Lambda \mathbb {k}$. Again, these morphisms can be glued up and give a $\mathbb {k}$-module sheaf $ {\mathcal {V}}\otimes _\Lambda \mathbb {k}$. By a similar argument, one can actually see this does not depend on the choice of lifts.

For $f\in \operatorname {Hom}_{\mathrm {Mod}^ {\mathfrak {I}}(\Lambda _X)}( {\mathcal {V}}, {\mathcal {W}})$, there exists a covering $\{U_i\}$ of $X$ with lifts $\{\tilde {f}_i\} \subset \mathrm {Mod}^ {\mathbb {R}}(\Lambda _{U_i})$. Then we get a set of morphisms $\{\tilde {f}_i\otimes _{\Lambda _X} \mathbb {k}_X\}$. One can see these are glued up to a morphism in $\mathrm {Mod}(\mathbb {k}_X)$ depending only on $f$ by a similar argument as above. The resulting morphism is denoted by $ {\mathfrak {F}}(f)$. It is clear that this correspondence preserves the compositions. Hence $ {\mathfrak {F}}$ gives a functor.

We would like to see the functor $ {\mathfrak {F}}$ is exact. Let

(6.2)\begin{equation} 0\rightarrow {\mathcal{V}}\xrightarrow{f} {\mathcal{W}}\xrightarrow{g} {\mathcal{X}}\rightarrow 0 \end{equation}

be an exact sequence in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$. It is equivalent to that there exists a locally finite open covering $\{U_i\}$ of $X$ such that we have an exact sequence

(6.3)\begin{equation} 0\rightarrow {\mathcal{V}}_i\xrightarrow{f_i} {\mathcal{W}}_i\xrightarrow{g_i} {\mathcal{X}}_i\rightarrow 0 \end{equation}

over each $U_i$. By Lemma 2.14, it can be lifted to an exact sequence of $ {\mathbb {R}}$-graded $\Lambda _X$-modules

(6.4)\begin{equation} 0\rightarrow \tilde{\mathcal{V}}_i\xrightarrow{\tilde{f}_i} \tilde{\mathcal{W}}_i\xrightarrow{\tilde{g}_i} \tilde{\mathcal{X}}_i\rightarrow 0. \end{equation}

Since tensor product is left exact, we get an exact sequence

(6.5)\begin{equation} \tilde{\mathcal{V}}_i\otimes_{\Lambda_X}\mathbb{k}_X\xrightarrow{\tilde{f}_i\otimes \operatorname{id}} \tilde{\mathcal{W}}_i\otimes_{\Lambda_X}\mathbb{k}_X\xrightarrow{\tilde{g}_i\otimes \operatorname{id}} \tilde{\mathcal{X}}_i\otimes_{\Lambda_X}\mathbb{k}_X\rightarrow 0. \end{equation}

It remains to show $\tilde {f}_i\otimes \operatorname {id}$ is injective. Let us take a homogeneous section of the kernel of $\tilde {f}_i\otimes \mathbb {k}$. Since it is a subsheaf of $\tilde {\mathcal{V} }_i\otimes _{\Lambda _X}\mathbb {k}_X$, it is locally represented by the form $s\otimes 1$. If $s\otimes 1$ is nonzero, it means that $T^a\cdot s\neq 0$ in $\tilde {\mathcal{V} }_i$. Hence we have $\Lambda _U\cdot s\hookrightarrow \tilde {\mathcal{V} }_i|_U$ where $U$ is the open set on which $s$ is defined. If $\tilde {f}_i(s)\otimes 1=0$, we have some $T^a$ such that $T^a\tilde {f}_i(s)=0$ by Lemma 2.7. Hence we have a sequence of morphisms over $U$ of $ {\mathbb {R}}$-graded $\Lambda$-modules

(6.6)\begin{equation} \Lambda_U\cdot s\rightarrow \tilde{\mathcal{V}}_i\xrightarrow{T^a\tilde{f}_i} \tilde{\mathcal{W}}_i\langle a\rangle \end{equation}

whose composition is zero. Since $\Lambda _U\cdot s$ is nonzero in $\mathrm {Mod}^{\mathfrak {I}}(U_i)$, the morphism $[T^a\tilde {f}_i]=[\tilde {f}_i]=f_i$ has a nontrivial kernel. This contradicts the injectivity of $f_i$. Hence $\tilde {f}_i\otimes \operatorname {id}$ is injective.

Lemma 6.2 Let $f\colon {({\bar {X}}, D_X)}\rightarrow {({\bar {Y}}, D_Y)}$ be a map between topological spaces with boundaries. Then we have

(6.7)\begin{equation} {\mathfrak{F}}\circ f^{{-}1}\cong f^{{-}1}\circ {\mathfrak{F}}. \end{equation}

Proof. For an $ {\mathbb {R}}$-graded $\Lambda _X$-module $ {\mathcal {V}}$, let us consider $f^{-1} {\mathcal {V}}$. The sheaf $ {\mathfrak {F}}\circ f^{-1} {\mathcal {V}}(U)$ is a sheaf associated with the presheaf

(6.8)\begin{equation} U\mapsto f^{{-}1}{\mathcal{V}}(U)\otimes_{\Lambda}\mathbb{k}. \end{equation}

On the other hand, the sheaf $f^{-1}\circ {\mathfrak {F}}( {\mathcal {V}})$ is a sheaf associated with the presheaf

(6.9)\begin{equation} U\mapsto f^{{-}1}({\mathcal{V}}\otimes_{\Lambda_X} \mathbb{k}_X)(U). \end{equation}

By the definition,

(6.10)\begin{align} f^{{-}1}{\mathcal{V}}(U)\otimes_{\Lambda}\mathbb{k}&\cong \bigg(\lim_{\substack{\longrightarrow \\ V\supset f(U)}}{\mathcal{V}}(V)\bigg) \otimes_\Lambda \mathbb{k}\nonumber\\ &\cong \lim_{\substack{\longrightarrow \\ V\supset f(U)}}({\mathcal{V}}(V)\otimes_{\Lambda}\mathbb{k})\nonumber\\ &\cong f^{{-}1}({\mathcal{V}}\otimes_{\Lambda_X} \mathbb{k}_X)(U). \end{align}

Hence they are the same.

Lemma 6.3 Let $ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ be an irregular local system. Then $ {\mathfrak {F}}( {\mathcal {V}})$ is a local system.

Proof. There exists an open covering of $U$ such that $ {\mathcal {V}}$ is represented by a direct sum of irregular constant sheaves $\Lambda ^\phi$. Hence the statement follows from that $\Lambda ^\phi \otimes _\Lambda \mathbb {k}$ is a rank 1 constant $\mathbb {k}$-module on any enough small open subset.

Lemma 6.4 Let $G\colon \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {Y}}, D_Y)})$ and $\tilde {G}\colon \mathrm {Mod}(\mathbb {k}_X)\rightarrow \mathrm {Mod}(\mathbb {k}_Y)$ be right (respectively left) exact functors such that $ {\mathfrak {F}}\circ G\cong G\circ {\mathfrak {F}}$. Then we have $ {\mathfrak {F}}\circ {\mathbb {R}} G\simeq {\mathbb {R}} \tilde {G}\circ {\mathfrak {F}}$ (respectively $ {\mathfrak {F}}\circ {\mathbb {L}} G\simeq {\mathbb {L}} \tilde {G}\circ {\mathfrak {F}}$).

Proof. Let $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ and take an injective resolution ${\mathcal {I}}^\bullet$ by using Proposition 4.2. Note that skyscraper sheaves $\Lambda _x$ used in this injective resolution are mapped to skyscraper sheaves $k_x$. Combining with the exactness of $ {\mathfrak {F}}$ (Lemma 6.1), we can conclude that $ {\mathfrak {F}}({\mathcal {I}}^\bullet )$ is an injective resolution of $ {\mathfrak {F}}( {\mathcal {V}})$. Hence we have

(6.11)\begin{equation} {\mathfrak{F}}\circ {\mathbb{R}} G({\mathcal{V}})\simeq {\mathfrak{F}}\circ G({\mathcal{I}}^\bullet)\simeq \tilde{G}\circ {\mathfrak{F}}({\mathcal{I}}^\bullet)\simeq {\mathbb{R}} \tilde{G}\circ {\mathfrak{F}}({\mathcal{V}}). \end{equation}

Similarly, for a free $ {\mathbb {R}}$-graded $\Lambda$-module ${\mathcal {F}}$, the module $ {\mathfrak {F}}({\mathcal {F}}_U)$ is a direct sum of $\mathbb {k}_U$, and hence is flat. By Lemma 4.4, we can do a similar argument as above. This completes the proof.

Lemma 6.5 Let $f$ be a proper map $X\rightarrow Y$. We have an equality

(6.12)\begin{equation} {\mathfrak{F}}\circ {\mathbb{R}} f_!\simeq {\mathbb{R}} f_!\circ {\mathfrak{F}} \end{equation}

of functors $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))\rightarrow D^b(\mathbb {k}_Y)$.

Proof. By Lemma 6.4, it is enough to show the underived version. For $ {\mathcal {V}}\in \mathrm {Mod}^ {\mathbb {R}}(\Lambda _X)$ and an open subset $U$, both $f_!\circ {\mathfrak {F}}( {\mathcal {V}})$ and $ {\mathfrak {F}}\circ f_!$ have $ {\mathcal {V}}(f^{-1}(U))\otimes \mathbb {k}$ over $U$. This completes the proof.

Lemma 6.6 Let $i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical map and $i_X\colon X\hookrightarrow {\bar {X}}$ be the inclusion. We have an equality

(6.13)\begin{equation} {\mathfrak{F}}\circ {\mathbb{R}} i_{{({\bar{X}}, D_X)} !}\simeq {\mathbb{R}} i_{X!}\circ {\mathfrak{F}}. \end{equation}

Proof. Again, we only prove the underived version. One can prove in a similar way to Lemma 6.5.

6.2 The case of irregular constructible sheaves

Proposition 6.7 The functor $ {\mathfrak {F}}$ restricts to a functor $\mathrm {Mod}_{ic}(\Lambda _X)\rightarrow \mathrm {Mod}_{c}(\mathbb {k}_X)$.

Proof. For $ {\mathcal {V}}\in \mathrm {Mod}_{ic}(\Lambda _X)$, let us take a stratification ${\mathcal {S}}$ of $X$. For each $S\in {\mathcal {S}}$, let us denote the inclusions by $i_{{(\bar {S}, D_S)}}\colon {(\bar {S}, D_S)}\hookrightarrow (X, \varnothing )$ and $i_S\colon S\hookrightarrow X$. Then we have $i_S^{-1} {\mathfrak {F}}( {\mathcal {V}})\cong {\mathfrak {F}}(i_{(\bar {S}, D_S)}^{-1}( {\mathcal {V}}))$ by Lemma 6.2. By Lemma 6.3, this is a local system. Hence $ {\mathfrak {F}}( {\mathcal {V}})$ is a constructible sheaf with respect to ${\mathcal {S}}$.

We also denote the induced functor $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))\rightarrow D^b(\mathrm {Mod}(\mathbb {k}_X))$ by $ {\mathfrak {F}}$.

Corollary 6.8 The functor $ {\mathfrak {F}}$ restricts to $D^b_{ic}(\Lambda _X)\rightarrow D^b_c(\mathbb {k}_X)$.

Proof. For $ {\mathcal {V}}^\bullet \in D^b(\mathrm {Mod}_{ic}(\Lambda _X))$, since $ {\mathfrak {F}}$ is exact on the abelian categories (Lemma 6.1), we have $H^i( {\mathfrak {F}}( {\mathcal {V}}^\bullet ))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))$. By Proposition 6.7, we have $ {\mathfrak {F}}(H^i( {\mathcal {V}}^\bullet ))\in \mathrm {Mod}_c(\mathbb {k}_X)$.

Lemma 6.9 If we have $ {\mathfrak {F}}(E)\simeq 0$ for an irregular constructible sheaf $E$, we have $E\simeq 0$.

Proof. We will argue on each stratum of a stratification of $E$. On the interior of a stratum, the irregular local system is locally isomorphic to ${\bigoplus} _{i\in I}\Lambda ^{\phi _i}$ for some $\phi _i$'s. Since $ {\mathfrak {F}}({\bigoplus} _i\Lambda ^{\phi _i})\cong \mathbb {k}^{|I|}$, $ {\mathfrak {F}}(E)\cong 0$ is equivalent to $|I|=0$. This means $E\cong 0$. This completes the proof.

We also would like to discuss the functor in the other direction. We consider the following functor

(6.14)\begin{equation} (-)\otimes_\mathbb{k} \Lambda\colon\mathrm{Mod}_{c}(\mathbb{k}_X)\rightarrow \mathrm{Mod}^0(\Lambda_X) \end{equation}

equipped with the trivial grading. We define $ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$ as the composition of the above with $[\cdot ]\colon \mathrm {Mod}^0(\Lambda _X)\rightarrow \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. It is clear that this induces an exact functor $ {\mathfrak {G}}\colon \mathrm {Mod}_{c}(\mathbb {k}_X)\rightarrow \mathrm {Mod}_{ic}(\Lambda _X)$. We will denote its derived functor by the same notation $ {\mathfrak {G}}\colon D^b_c(\mathbb {k}_X)\rightarrow D^b_{ic}(\Lambda _X)$.

Proposition 6.10 We have $ {\mathfrak {F}}\circ {\mathfrak {G}}\simeq \operatorname {id}$.

Proof. This again follows from the fact that $ {\mathfrak {F}}(\Lambda ^\phi )$ is a rank 1 constant $\mathbb {k}$-module.

7. Enhanced sheaves and $\Lambda$-modules

7.1 $\mathbb{R}$-constructible enhanced ind-sheaves

In this section, we recall the definition of $ {\mathbb {R}}$-constructible enhanced ind-sheaves. For more detailed accounts, we refer to the original [DK16] and the survey [KS16]. Let $M$ be a real analytic manifold. Let $\bar {\mathbb{R} }$ be the two point compactification of $ {\mathbb {R}}$ i.e. $ {\mathbb {R}}\cong (0,1)\hookrightarrow [0,1]=\bar {\mathbb{R} }$. The category of enhanced ind-sheaves is defined in two steps. First, we set

(7.1)\begin{equation} D^b(\mathrm{I}\mathbb{k}_{M\times(\bar{\mathbb{R}},{\mathbb{R}})}):=D^b(\mathrm{I}\mathbb{k}_{M\times\bar{\mathbb{R}}})/D^b(\mathrm{I}\mathbb{k}_{M\times{\bar{\mathbb{R}}{\backslash} {\mathbb{R}}}}) \end{equation}

where $D^b(\mathrm {I}\mathbb {k}_M)$ is the bounded derived category of ind-sheaves over $M$ [KS01]. We set $\mathbb {k}_{t\lesseqgtr 0}:=\mathbb {k}_{\{ (x,t)\in M\times \bar {\mathbb{R} }| t\in {\mathbb {R}}, t\lesseqgtr 0 \}}$. The definition of the convolution product $\overset {+}{\otimes }$ can be extended to the objects in $D^b(\mathrm {I}\mathbb {k}_{M\times (\bar {\mathbb{R} }, {\mathbb {R}})})$. We set

(7.2)\begin{equation} \mathrm{IC}_{t^*=0}:=\big\{ K\,|\, K\overset{+}{\otimes} \mathbb{k}_{\leqslant 0}\simeq 0, K\overset{+}{\otimes} \mathbb{k}_{\geqslant 0}\simeq 0\big\}. \end{equation}

The category of enhanced ind-sheaves over $X$ is defined by

(7.3)\begin{equation} E^b({\mathrm{I}\mathbb{k}_M}):=D^b(\mathrm{I}\mathbb{k}_{M\times {\mathbb{R}}_\infty})/\mathrm{IC}_{t^*=0}. \end{equation}

The triangulated category $E^b(\mathrm {I}\mathbb {k}_M)$ has monoidal operations $\overset {+}{\otimes }$ and $\mathcal{I} hom^+$. For a morphism $M\rightarrow N$ of real analytic manifolds, there are associated functors

(7.4)\begin{gather} Ef_{!!}, Ef_*\colon E^b(\mathrm{I}\mathbb{k}_M)\rightarrow E^b(\mathrm{I}\mathbb{k}_N), \end{gather}

(7.5)\begin{gather}Ef^{{-}1}, Ef^!\colon E^b(\mathrm{I}\mathbb{k}_N)\rightarrow E^b(\mathrm{I}\mathbb{k}_M). \end{gather}

They form adjoint pairs $Ef_{!!}\dashv Ef^!$ and $Ef^{-1}\dashv Ef_*$.

We further set

(7.6)\begin{equation} \mathbb{k}^E_M:=\underset{a \rightarrow\infty}{\text{`$\lim$'}}\,\mathbb{k}_{t\geqslant a} \end{equation}

as an object of $E^b({\mathrm {I}\mathbb {k}_M})$. As usual, $\text{`}\lim\text{'}$ means Ind-colimit.

Definition 7.1

1. (i) An object ${\mathcal {E}}$ of $E^b({\mathrm {I}\mathbb {k}_M})$ is said to be $ {\mathbb {R}}$-constructible if there exists an open covering $\{U_i\}$ of $M$ such that there exists an $ {\mathbb {R}}$-constructible sheaf ${\mathcal {E}}_U$ over each $U\times {\mathbb {R}}$ such that ${\mathcal {E}}|_{U\times \bar {\mathbb{R} }}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_{U}$.

2. (ii) An enhanced $ {\mathbb {R}}$-constructible ind-sheaf ${\mathcal {E}}$ of $E^b({\mathrm {I}\mathbb {k}_M})$ is said to be ${\mathbb {C}}$-constructible if the following holds. There exists an open covering $\{U\}$ of $M$ and a ${\mathbb {C}}$-stratification ${\mathcal {S}}_U$ for each $U$ such that: (i) there exists an $ {\mathbb {R}}$-constructible sheaf ${\mathcal {E}}_{U_i}$ such that ${\mathcal {E}}|_{U \times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes }\mathbb {k}^E_U$; (ii) each cohomology sheaf ${\mathcal {H}}^i({\mathcal {E}}_U|_S)$ for each $S\in {\mathcal {S}}_U$ is isomorphic to a direct sum of sheaves of the form $\mathbb {k}_{t\geqslant \phi (x)}$ for some continuous function $\phi$.

We denote the full subcategory spanned by $ {\mathbb {R}}$-constructible (respectively ${\mathbb {C}}$-constructible) enhanced ind-sheaves by $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ (respectively $E^b_{{\mathbb {C}} - c}(\mathrm {I}\mathbb {k}_M)$). The category $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_M)$ has a contravariant autoequivalence ${\mathbb {D}}$, analogous to the Verdier duality.

7.2 From enhanced sheaves to $\Lambda$-modules

For a sheaf ${\mathcal {E}}$ on $X\times \bar {\mathbb{R} }$, let us consider the object ${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ where $p\colon X\times {\mathbb {R}}\rightarrow X$ is the projection. It is equipped with the action of $\Lambda$ as follows. The action of $T^b$ on ${\bigoplus} _{-a\in {\mathbb {R}}}p_*\Gamma _{[-a,\infty )}{\mathcal {E}}$ is the product of

(7.7)\begin{equation} p_*\Gamma_{[{-}a,\infty)}{\mathcal{E}}\rightarrow p_*\Gamma_{[{-}b-a,\infty)}{\mathcal{E}} \end{equation}

induced by the canonical map $\mathbb {k}_{[-b-a,\infty )}\rightarrow \mathbb {k}_{[-a,\infty )}$.

Recall that $D^b(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}})$ is the derived category of $\mathrm {Mod}(I\mathbb {k}_{M\times \bar { {\mathbb {R}}}}):=\mathrm {Ind}(\mathrm {Mod}_c(\mathbb {k}_{M\times \bar { {\mathbb {R}}}}))$ where $c$ means compactly supported sheaves. The left exact functor

(7.8)\begin{equation} \mathrm{Mod}_c(\mathbb{k}_{M\times \bar{{\mathbb{R}}}})\rightarrow \mathrm{Mod}^{\mathfrak{I}}(\Lambda_X); {\mathcal{E}}\mapsto \bigg[\bigoplus_{-a\in {\mathbb{R}}}p_*\Gamma_{[{-}a, \infty)}{\mathcal{E}}\bigg] \end{equation}

induces

(7.9)\begin{equation} \tilde{M}\colon \mathrm{Mod}(\mathrm{I}\mathbb{k}_{X\times \bar{\mathbb{R}}})\rightarrow \mathrm{Ind}(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)) \end{equation}

by taking $\mathrm {Ind}$ of all of them. This is again left exact [KS06].

We denote the right derived functor of $\tilde {M}$ by $ {\mathbb {R}}\tilde {M}\colon D^b(\mathrm {I}\mathbb {k}_{X\times \bar {\mathbb{R} }})\rightarrow D^b(\mathrm {Ind}(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)))$. Recall that there exist embeddings

(7.10)\begin{equation} (-)\overset{+}{\otimes} \mathbb{k}_{t\geqslant 0}\colon E^b(\mathrm{I}\mathbb{k}_X)\rightarrow D^b(\mathrm{I}\mathbb{k}_{(X\times\bar{\mathbb{R}}, X\times {\mathbb{R}})}) \end{equation}

and

(7.11)\begin{equation} (-)\otimes \mathbb{k}_{X\times {\mathbb{R}}}\colon D^b(\mathrm{I}\mathbb{k}_{(X\times \bar{\mathbb{R}}, X\times {\mathbb{R}})})\rightarrow D^b(\mathrm{I}\mathbb{k}_{X\times \bar{\mathbb{R}}}). \end{equation}

Composing these with $ {\mathbb {R}}\tilde {M}$, we get

(7.12)\begin{equation} M:={\mathbb{R}}\tilde{M}(((-)\overset{+}{\otimes} \mathbb{k}_{\geqslant 0})\otimes \mathbb{k}_{X\times {\mathbb{R}}})\colon E^b(\mathrm{I}\mathbb{k}_X)\rightarrow D^b(\mathrm{Ind}(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X))). \end{equation}

Lemma 7.2 Let ${\mathcal {E}}$ be an $ {\mathbb {R}}$-constructible sheaf over $X\times {\mathbb {R}}$. Then we have $M({\mathcal {E}}\overset {+}{\otimes } \mathbb {k}^E_X)\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$.

Proof. By the definition of $M$ and $\mathbb {k}^E_X$, it is enough to show that the natural morphisms

(7.13)\begin{equation} \bigg[ \bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a,\infty)}{\mathcal{E}}\bigg] \rightarrow \bigg[ \bigoplus_{-a\in {\mathbb{R}}} {\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,\infty)}{\mathcal{E}}\bigg] \end{equation}

are isomorphisms for any $c\in \mathbb{R} _{\geqslant 0}$. The cone is given by

(7.14)\begin{equation} \bigg[\bigoplus_{-a\in {\mathbb{R}}}{\mathbb{R}} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[{-}a-c,-a)}{\mathcal{E}}\bigg]. \end{equation}

Since $T^c\in \Lambda$ vanishes on this object, this is zero. Hence the morphisms are isomorphisms.

Lemma 7.3 The functor $M$ restricts to a functor $E^b_{ {\mathbb {R}} - c}(\mathrm {I}\mathbb {k}_X)\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$, which is also denoted by $M$.

Proof. For an $ {\mathbb {R}}$-constructible enhanced ind-sheaf ${\mathcal {E}}$, there exists a locally finite covering ${\mathcal {U}}$ of $X$ such that we have ${\mathcal {E}}|_{U\times {\mathbb {R}}}\simeq {\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U$ and $(n+2)$-fold covers are empty where $n=\dim X$. By the Cech construction, ${\mathcal {E}}$ is represented by a result of mapping cones of $i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}^E_U)$. This implies $\tilde {M}({\mathcal {E}})$ is obtained as a finite mapping cones of $\tilde {M}(i_!({\mathcal {E}}_U\overset {+}{\otimes } \mathbb {k}_U^E))$. By Lemma 7.2, this means that $\tilde {M}({\mathcal {E}})$ is in $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$. This completes the proof.

Let $S$ be a locally closed subset in $X$ and $\bar {S}$ be the closure of $S$ in $X$ and set $D_S:=\bar {S}{\backslash } S$. Let $\phi$ be a continuous ${\mathbb {C}}$-valued function on $S$. The inclusion $i_{(\bar {S}, D_S)}\colon {(\bar {S}, D_S)}\rightarrow X$ is a tame map, we get $i_{{(\bar {S}, D_S)} !}\Lambda ^\phi _{(\bar {S}, D_S)}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _X)$. We also set ${\mathcal {E}}^\phi :=\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}\overset {+}{\otimes } \mathbb {k}^E_X\in E^b(\mathrm {I}\mathbb {k}_X)$.

Lemma 7.4 We have $M({\mathcal {E}}^\phi )\cong i_{{(\bar {S}, D_S)} !}\Lambda ^\phi$.

Proof. By the definition of $M$, $M({\mathcal {E}}^\phi )\cong \underset {a \rightarrow \infty }{\text {`{$\lim$ }'}}\big ( {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t+a}\big )$. From the proof of Lemma 7.2, this colimit stabilizes. In particular, $M({\mathcal {E}}^\phi )\cong {\bigoplus} _{-c\in {\mathbb {R}}} {\mathbb {R}} p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[-c, -\infty )}\mathbb {k}_{ {\mathop {\mathfrak {Re}}\nolimits } \phi \leqslant t}=:i_{{(\bar {S}, D_S)}!}\Lambda ^\phi$

Lemma 7.5 There exists a canonical isomorphism

(7.15)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)}(i_{{(\bar{S}, D_S)} !}\Lambda^{\phi}, i_{{(\bar{S}, D_S)} !}\Lambda^{\phi'})\cong \operatorname{Hom}_{E^b(\mathrm{I}\mathbb{k}_X)}({\mathcal{E}}^\phi, {\mathcal{E}}^{\phi'}). \end{equation}

Proof. By Lemmas 5.11 and 5.12, we have

(7.16)\begin{equation} \operatorname{Hom}_{\mathrm{Mod}^{\mathfrak{I}}(\Lambda_X)}(i_{{(\bar{S}, D_S)} !}\Lambda^{\phi}, i_{{(\bar{S}, D_S)} !}\Lambda^{\phi'})\cong \begin{cases} \mathbb{k} & \text{$\max\{0, {\mathop{\mathfrak{Re}}\nolimits}\phi-{\mathop{\mathfrak{Re}}\nolimits}\phi'\}$ is bounded,}\\ 0 & \text{otherwise.} \end{cases} \end{equation}

It is easy to see that the right-hand side of (7.15) also has the same formula. In the case that $\max \{0, {\mathop {\mathfrak {Re}}\nolimits }\phi - {\mathop {\mathfrak {Re}}\nolimits }\phi '\}$ is bounded, there exists $c\in \mathbb{R} _{\geqslant 0}$ such that $ {\mathop {\mathfrak {Re}}\nolimits }\phi < {\mathop {\mathfrak {Re}}\nolimits }\phi '+c$ everywhere. For a map $f\in \operatorname {Hom}_{E^b(\mathrm {I}\mathbb {k}_X)}({\mathcal {E}}^\phi , {\mathcal {E}}^{\phi '})$, we have a lift $\tilde {f}\colon \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi (x)\}}\rightarrow \mathbb {k}_{\{ t\geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '(x)+c\}}$ of usual $ {\mathbb {R}}$-constructible sheaves. Then $\tilde {f}$ induces a morphism $i_{{(\bar {S}, D_S)} !}\Lambda ^\phi \rightarrow i_{{(\bar {S}, D_S)} !}\Lambda ^{\phi '}$. It is easy to see that the induced morphism only depends on the choice of $f$. By the proof of Lemma 5.11, this gives an isomorphism.

8. Irregular Riemann–Hilbert correspondence

In this section, we will prove our version of the irregular Riemann–Hilbert correspondence as a corollary of D’Agnolo and Kashiwara's one. In this section, we will work over ${\mathbb {C}}$.

8.1 An example

Before going to the general case, we would like to see some examples of the correspondence in $\dim =1$. We will freely use the standard language of Stokes phenomenon, for which one can refer to the standard reference, for example, [Sib90].

We will consider the case when $X={\mathbb {D}}$ a disk around $0\in {\mathbb {C}}$. Let ${\mathcal {M}}$ be a meromorphic connection with poles in $0\in {\mathbb {D}}$. For the simplicity of the exposition, we assume that the formal completion of ${\mathcal {M}}$ at $0$ is decomposed as ${\bigoplus} _{\phi \in \Phi } {\mathcal {E}}(\phi )$ where $\Phi$ is a set of meromorphic functions with poles in $0\in {\mathbb {D}}$, ${\mathcal {E}}(\phi )$ is a connection defined by $d+\phi$. The set $\Phi$ give a sectorial decomposition ${\mathbb {D}}{\backslash } 0={\bigcup} S_i$ by the Stokes rays and there exists a complete set of solutions $\{s_{\phi }^i\}$ on each $S_i$. On each Stokes ray, we have a transformation matrix between the sets of solutions. The transformed $s_\phi$ can have a component of $s_{\phi '}$ only if $ {\mathop {\mathfrak {Re}}\nolimits }\phi \geqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$ on the ray. We denote the transformation matrix on the Stokes ray $r$ by $S_r$.

Since

(8.1)\begin{equation} \operatorname{Hom}(\Lambda^\phi, \Lambda^{\phi'})=\mathbb{k}, \operatorname{Hom}(\Lambda^{\phi'}, \Lambda^{\phi})=0 \end{equation}

if $ {\mathop {\mathfrak {Re}}\nolimits }\phi \leqslant {\mathop {\mathfrak {Re}}\nolimits }\phi '$, we can represent the transposition of $S_r$ in $\operatorname {End}({\bigoplus} \Lambda ^\phi )$, as an isomorphism, locally around the ray $r$. Gluing up ${\bigoplus} _\phi \Lambda ^\phi$ by the these morphisms, we get the Riemann–Hilbert dual object (i.e. the image of the ‘de Rham’ functor) of ${\mathcal {M}}$ in terms of irregular constructible sheaves.

Of course, by the same procedure just replacing $\Lambda ^\phi$ with ${\mathcal {E}}^\phi$ produces an enhanced ind-sheaf corresponding ${\mathcal {E}}$ to by D’Agnolo and Kashiwara's functor [DK16].

8.2 Notation for analytic ${\mathcal {D}}$-modules

We refer the theory of analytic ${\mathcal {D}}$-modules to [Kas03]. In this subsection, we simply recall the notation. For a complex manifold, ${\mathcal {D}}_X$ is the sheaf of differential operators, $\mathrm {Mod}({\mathcal {D}}_X)$ is the category of left ${\mathcal {D}}$-modules, and $D^b({\mathcal {D}}_X)$ is the bounded derived category of ${\mathcal {D}}$-modules. We denote the full subcategory of $D^b({\mathcal {D}}_X)$ spanned by cohomologically holonomic ${\mathcal {D}}$-modules by $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.

The duality functor ${\mathbb {D}}$ is a contravariant autoequivalence of $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$. For a morphism of complex manifolds $f\colon X\rightarrow Y$, we can define the following functors,

(8.2)\begin{gather} \int_{f}\colon D^b({\mathcal{D}}_X)\rightarrow D^b({\mathcal{D}}_Y); {\mathcal{M}}\mapsto {\mathbb{R}} f_*({\mathcal{D}}_{X\leftarrow Y}\otimes^{\mathbb{L}}_{{\mathcal{D}}_X}{\mathcal{M}}), \end{gather}

(8.3)\begin{gather}f^{\dagger}\colon D^b({\mathcal{D}}_Y)\rightarrow D^b({\mathcal{D}}_X);{\mathcal{N}}\mapsto {\mathcal{D}}_{Y\rightarrow X}\otimes^{\mathbb{L}}_{f^{{-}1}{\mathcal{D}}_Y}f^{{-}1} {\mathcal{N}}[\dim X-\dim Y], \end{gather}

by using transfer ${\mathcal {D}}$-modules ${\mathcal {D}}_{X\leftarrow Y}$ and ${\mathcal {D}}_{X\rightarrow Y}$. The functor $f^{\dagger}$ always preserves cohomologically holonomic modules. If $f$ is proper, $\int _f$ also preserves cohomologically holonomic modules. For a proper $f$, the pair of functors form an adjoint pair $\int _f \dashv f^{\dagger}$. We also set $f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}\colon D^b_{\mathrm {hol}}({\mathcal {D}}_Y)\rightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and $f_\star :={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then $f^\star \dashv f_\star$

8.3 Irregular Riemann–Hilbert correspondence using enhanced sheaves

We recall the irregular Riemann–Hilbert correspondence by the result of D'Agnolo and Kashiwara.

Theorem 8.1 [DK16]

There exists a contravariant embedding

(8.4)\begin{equation} \mathrm{Sol}^E\colon D^b_{\mathrm{hol}}({\mathcal{D}}_X)\hookrightarrow E^b_{{\mathbb{R}} - c}(\mathrm{I}{\mathbb{C}}_X). \end{equation}

Our convention is slightly different from the original one in [DK16]. Let $\mathrm {Sol}^{{\mathbb {E}}}$ be the original one. We set $\mathrm {Sol}^E:=\mathrm {Sol}^{\mathbb {E}}[\dim X]$ We have $\mathrm {Sol}^E:={\mathbb {D}}\circ {\mathrm {DR}}^E$ where ${\mathrm {DR}}^E$ is the same as the original one. We collect some properties of the irregular Riemann–Hilbert correspondence as follows.

Proposition 8.2 [DK16, Theorem 9.4.8, Proposition 9.4.10]

1. (i) There exists a canonical isomorphism ${\mathbb {D}}\circ {\mathrm {DR}}^E\simeq {\mathrm {DR}}^E\circ {\mathbb {D}}$.

2. (ii) For a morphism $f\colon X\rightarrow Y$ of complex manifolds, there exists an isomorphism ${\mathrm {DR}}^E\circ f^{\dagger} \simeq Ef^!\circ {\mathrm {DR}}^E$.

3. (iii) For a proper map $f\colon X\rightarrow Y$, we have ${\mathrm {DR}}^E\circ \int _f\simeq Ef_*\circ {\mathrm {DR}}^E$.

4. (iv) There exists an isomorphism $\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$ for ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$.

We will also use the following fundamental result. Let $Y$ be an analytic hypersurface of the complex manifold $X$. Take a meromorphic function $\phi$ with poles in $Y$; $\phi \in {\mathcal {O}}_X(*Y)$. We set ${\mathcal {E}}(\phi ):=({\mathcal {D}}_X\cdot e^\phi )(*Y)$.

Our convention for $\mathrm {Sol}^E$ is shifted from D’Agnolo and Kashiwara's one so that the following holds.

Proposition 8.3 [DK16, Lemma 9.3.1]

There exists an isomorphism

(8.5)\begin{equation} \mathrm{Sol}^E({\mathcal{E}}(\phi))\simeq k^E_X\overset{+}{\otimes} k_{t\geqslant {\mathop{\mathfrak{Re}}\nolimits}\phi(x)}[\dim X]. \end{equation}

8.4 Irregular Riemann–Hilbert correspondence

Let us denote the essential image of $\mathrm {Sol}^E$ by $E^b_{{\mathcal {D}}}(\mathrm {I}{\mathbb{C}} _X)$.

Lemma 8.4 The object $M({\mathcal {E}})$ is irregular constructible for ${\mathcal {E}}\in E^b_{\mathcal {D}}(\mathrm {I}{\mathbb{C}} _X)$.

Proof. We will prove by induction on the dimension of the support.

Let us take a holonomic ${\mathcal {D}}$-module ${\mathcal {M}}$ and consider ${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$.

If the dimension of the support of $M({\mathcal {E}})$ is zero-dimensional, it is irregular constructible. We suppose that the statement is true for any ${\mathcal {E}}'$ with $\dim \mathrm {supp}\, M({\mathcal {E}}')<\dim \mathrm {supp}\, M({\mathcal {E}})$.

Since the question is local, we work locally. We set $Y:=\mathrm {supp}\,(M({\mathcal {E}}))$. Let $\pi \colon Y'\rightarrow Y$ be a resolution of singularities of $Y$. Let $D$ be the inverse image of the union of singularities of $Y$ and ${\mathcal {M}}$. Then there exists a canonical morphism

(8.6)\begin{equation} {\mathcal{M}}_1\rightarrow {\mathcal{M}}_1':=\pi_\star (\pi^\star{\mathcal{M}})(*D). \end{equation}

Since $(\pi ^\star {\mathcal {M}})(*D)$ is a meromorphic connection, $M(\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D)))$ is irregular constructible. Note that $\mathrm {Sol}^E(\pi ^\star {\mathcal {M}}(*D))$ has its support in the complement of $D$. Hence $M(\mathrm {Sol}^E({\mathcal {M}}_1'))$ has its support in the complement of $\pi (D)$ and is irregular constructible. The cone $C$ of this morphism is living on a divisor of $Y$. By the induction hypothesis, $M(\mathrm {Sol}^E(C))$ is irregular constructible. This completes the proof.

Lemma 8.5 For an irregular local system $ {\mathcal {V}}$, there exists an enhanced ind-sheaf $N( {\mathcal {V}})$ such that $M(N( {\mathcal {V}}))\cong {\mathcal {V}}$.

Proof. For an irregular local system $ {\mathcal {V}}$, one can find a sectorial covering (Definition 5.21). On each open subset in the covering, we have ${\bigoplus} {\mathcal {V}}\cong \Lambda ^\phi$. By Lemma 7.5, we can glue up ${\bigoplus} {\mathcal {E}}^\phi$ by the corresponding morphisms gluing ${\bigoplus} \Lambda ^\phi$ up to make $ {\mathcal {V}}$. We denote the resulting enhanced ind-sheaf by $N( {\mathcal {V}})$.

Since the functor $M$ maps ${\mathcal {E}}^\phi$ to $\Lambda ^\phi$ (Lemma 7.4) and the gluing maps are translated by Lemma 7.5, the enhanced ind-sheaf $N( {\mathcal {V}})$ satisfies $MN( {\mathcal {V}})\cong {\mathcal {V}}$.

Our version of an irregular Riemann–Hilbert correspondence is the following.

Theorem 8.6 The functor $M$ is a contravariant exact equivalence:

(8.7)\begin{equation} M\colon E^b_{{\mathcal{D}}}(\mathrm{I}{\mathbb{C}}_X)\xrightarrow{\simeq} D^b_{ic}(\Lambda_X). \end{equation}

In particular, there exists a contravariant equivalence

(8.8)\begin{equation} \mathrm{Sol}^\Lambda:=M\circ \mathrm{Sol}^E\colon D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq}D^b_{ic}(\Lambda_X). \end{equation}

Proof. First, we will prove the full faithfulness. Let ${\mathcal {M}}, {\mathcal {N}}$ be holonomic ${\mathcal {D}}_X$-modules. Set ${\mathcal {E}}:=\mathrm {Sol}^E({\mathcal {M}})$ and ${\mathcal {F}}:=\mathrm {Sol}^E({\mathcal {N}})$. Then we have

(8.9)\begin{equation} \operatorname{Hom}({\mathcal{M}}, {\mathcal{N}})\cong \operatorname{Hom}({\mathcal{F}}, {\mathcal{E}}). \end{equation}

We would like to prove

(8.10)\begin{equation} \operatorname{Hom}({\mathcal{F}}, {\mathcal{E}})\cong \operatorname{Hom}(M({\mathcal{F}}), M({\mathcal{E}})). \end{equation}

Take a common stratification for ${\mathcal {E}}, {\mathcal {F}}$ and $i\colon U\hookrightarrow X$ be the open stratum and $j\colon V\hookrightarrow X$ be the complement. Then by Lemma 4.24, we have an exact triangle

(8.11)\begin{equation} \operatorname{Hom}(j^{{-}1}M({\mathcal{F}}), j^{{-}1}M({\mathcal{E}})) \rightarrow\operatorname{Hom}(M({\mathcal{F}}), M({\mathcal{E}}))\rightarrow \operatorname{Hom}(i^{{-}1}M({\mathcal{F}}),i^{{-}1}M({\mathcal{E}}))\rightarrow. \end{equation}

We also have the corresponding recollement for enhanced ind-sheaves

(8.12)\begin{equation} \operatorname{Hom}(Ej^{{-}1}{\mathcal{F}}, Ej^{{-}1}{\mathcal{E}})\rightarrow \operatorname{Hom}({\mathcal{F}}, {\mathcal{E}})\rightarrow \operatorname{Hom}({\mathcal{F}}\overset{+}{\otimes} \mathbb{k}_{U\times {\mathbb{R}}_{\geqslant 0}}, {\mathcal{E}}\overset{+}{\otimes} \mathbb{k}_{U\times {\mathbb{R}}_{\geqslant 0}}) \rightarrow \end{equation}

which is a direct consequence of the recollement on $X\times {\mathbb {R}}$. By the construction, this is the image of (8.11) under $M$. Hence, it is enough to show the full faithfulness for irregular local systems.

For an irregular local system, we have locally a sectorial covering such that ${\mathcal {E}}, {\mathcal {F}}$ have the form ${\bigoplus} {\mathcal {E}}^\phi$, $M({\mathcal {E}}), M({\mathcal {F}})$ have the form ${\bigoplus} \Lambda ^\phi$, and these are related by Lemma 7.4. Hence we have the full faithfulness on each open cover by Lemma 7.5. Note also that $M$ is a morphism between stacks, which is clear from the definition. Hence we can glue up these isomorphisms to get the global full faithfulness.

To prove the essential surjectivity, we will use Mochizuki's curve test criterion [Moc16]. Since $\mathrm {Sol}^\Lambda$ is a fully faithful exact functor, by the recollement 4.24, it is enough to see $\mathrm {Sol}^\Lambda$ hits each irregular local system.

Let $ {\mathcal {V}}$ be an irregular local system on ${(\bar {S}, D_S)}\subset X$. Let $\phi \colon \mathbf {D} \rightarrow X$ be a holomorphic disk satisfying $\phi ^{-1}(D_S)=\{ 0\}$. We set $x:=\phi (0)$.

By the construction, $N( {\mathcal {V}})$ of Lemma 8.5 has a sectorial covering around $x$ equipped with a set of multi-valued meromorphic functions. The pull-back of a sectorial covering is again sectorial. Hence $E\phi ^{-1}N( {\mathcal {V}})$ has a sectorial covering on which $E\phi ^{-1}N( {\mathcal {V}})$ restricts to the form ${\bigoplus} {\mathcal {E}}^\phi$ and the gluing data is the Stokes data. Since the situation is now one-dimensional, it is standard to see this is in the image of $\mathrm {Sol}^E$ (e.g. by the discussion of [DK19, 9.8]). Then Mochizuki's theorem [Moc16] tells us that there exists an object in $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ such that $\mathrm {Sol}^E({\mathcal {M}})=N( {\mathcal {V}})$. Hence we have $\mathrm {Sol}^\Lambda ({\mathcal {M}})=M\circ N( {\mathcal {V}})= {\mathcal {V}}$. This proves the essential surjectivity.

Corollary 8.7 There exists an exact equivalence

(8.13)\begin{equation} {\mathrm{DR}}^\Lambda:={\mathbb{D}}\circ \mathrm{Sol}^\Lambda\colon D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq} D^b_{ic}(\Lambda_X). \end{equation}

Proof. This is the composition of equivalences from Theorem 8.6 and Corollary 5.37.

In [DK16], it is proved that the composition of $i_{\mathrm {reg}}\colon D^b_{\mathrm {reghol}}({\mathcal {D}}_X)\hookrightarrow D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and $\mathrm {Sol}^E$ is the same as the composition of the regular Riemann–Hilbert solution functor $\mathrm {Sol}$ and $D^b_c({\mathbb {C}}_X)\hookrightarrow E^b(\mathrm {I}{\mathbb{C}} _X)$. Here the last inclusion is obtained as $(\pi ^{-1}(-)\otimes {\mathbb {C}}_{X\times _{ {\mathbb {R}}_{\geqslant 0}}})\overset {+}{\otimes } {\mathbb {C}}^E_X$ where $\pi \colon M\times \bar { {\mathbb {R}}}\rightarrow M$. By the definition of $M$, the following corollary is clear.

Corollary 8.8 We have an identification $ {\mathfrak {G}}\circ \mathrm {Sol}\cong \mathrm {Sol}^\Lambda \circ i_{\mathrm {reg}}$.

8.5 Functors

In this subsection, we prove the commutativity between $\mathrm {Sol}^\Lambda$ and various functors. We assume that all the spaces are without boundary in this subsection.

Proposition 8.9 Let $f\colon X\rightarrow Y$. We have

(8.14)\begin{equation} M\circ Ef^*\simeq f^{{-}1}\circ M. \end{equation}

In particular,

(8.15)\begin{equation} \mathrm{Sol}^\Lambda\circ f^{\dagger}{\simeq} f^{{-}1}\circ \mathrm{Sol}^\Lambda. \end{equation}

Proof. Since we know $Ef^*$ commutes with $\mathrm {Sol}^E$, it is enough to see the commutativity with the functor $M$. Let us take an $ {\mathbb {R}}$-constructible sheaf ${\mathcal {E}}$ on $X\times \bar {\mathbb{R} }$. Let $\bar {f}$ be the direct product of $f\colon X\rightarrow Y$ and $\operatorname {id}\colon \bar {\mathbb{R} }\rightarrow \bar {\mathbb{R} }$. Then we have

(8.16)\begin{equation} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{X\times [a, \infty)}(\bar{f}^{{-}1}{\mathcal{E}})\simeq f^{{-}1}p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{Y\times [a,\infty)}{\mathcal{E}}. \end{equation}

Hence we have $M(\bar {f}^{-1}{\mathcal {E}})\simeq f^{-1}M({\mathcal {E}})$. This proves the first line.

Lemma 8.10 We have

(8.17)\begin{equation} M(-\boxtimes -)\simeq M(-)\boxtimes M(-). \end{equation}

For ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$ and ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have

(8.18)\begin{equation} \mathrm{Sol}^\Lambda({\mathcal{M}}\boxtimes {\mathcal{N}})\simeq \mathrm{Sol}^\Lambda({\mathcal{M}})\boxtimes \mathrm{Sol}^\Lambda({\mathcal{N}}). \end{equation}

Proof. By [DK16], we have $\mathrm {Sol}^E({\mathcal {M}}\boxtimes {\mathcal {N}})\simeq \mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}})$. Hence it suffices to prove $M(\mathrm {Sol}^E({\mathcal {M}})\overset {+}{\boxtimes }\mathrm {Sol}^E({\mathcal {N}}))\simeq M(\mathrm {Sol}^E({\mathcal {M}}))\boxtimes M(\mathrm {Sol}^E({\mathcal {N}}))$.

First, note that we have $p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{[a,\infty )}({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})\simeq p_*\mathop { {\mathbb {R}}\Gamma }\nolimits _{t_1+t_2\geqslant a}({\mathcal {E}}\boxtimes {\mathcal {F}})$. We also have a map

(8.19)\begin{equation} p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{[b, \infty)\times [c, \infty)}({\mathcal{E}}\boxtimes {\mathcal{F}})\rightarrow p_*\mathop{{\mathbb{R}}\Gamma}\nolimits_{t_1+t_2\geqslant b+c}({\mathcal{E}}\boxtimes {\mathcal{F}}). \end{equation}

By combining these, we get a map $M({\mathcal {E}})\boxtimes M({\mathcal {F}})\rightarrow M({\mathcal {E}}\overset {+}{\boxtimes } {\mathcal {F}})$. It suffices to show that this map is locally an isomorphism. For enhanced ind-sheaves ${\mathcal {E}}^{\phi _1}, {\mathcal {E}}^{\phi _2}$, we have ${\mathcal {E}}^{\phi _1}\overset {+}{\boxtimes } {\mathcal {E}}^{\phi _2}\simeq {\mathcal {E}}^{\phi _1\oplus \phi _2}$. We also have $\Lambda ^{\phi _1}\boxtimes \Lambda ^{\phi _2}\cong \Lambda ^{\phi _1\oplus \phi _2}$ from Lemma 5.13. Hence the morphism $M({\mathcal {E}}^{\phi _1})\boxtimes M({\mathcal {E}}^{\phi _2})\rightarrow M({\mathcal {E}}^{\phi _1\oplus \phi _2})$ is an isomorphism. The general case can be reduced to this case by considering on each stratum.

Proposition 8.11 For ${\mathcal {M}}, {\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, we have

(8.20)\begin{equation} \mathrm{Sol}^\Lambda({\mathcal{M}}\otimes {\mathcal{N}})\simeq \mathrm{Sol}^\Lambda({\mathcal{M}})\otimes \mathrm{Sol}^\Lambda({\mathcal{N}})[-\dim X]. \end{equation}

We also have

(8.21)\begin{equation} M\circ \mathop{{{\mathcal{H}}}om}\nolimits^E(-,-)\simeq \mathop{{{\mathcal{H}}}om}\nolimits(M(-), M(-)) \end{equation}

on $E^b_{{\mathcal {D}}}(\mathrm {I}\mathbb {k}_X)$

Proof. Let $\delta \colon X\rightarrow X\times X$ be the diagonal embedding. Then ${\mathcal {M}}\otimes {\mathcal {N}}\cong \delta ^{{\dagger} }({\mathcal {M}}\boxtimes {\mathcal {N}})$. Then we have,

(8.22)\begin{align} \mathrm{Sol}^\Lambda(\delta^{{{\dagger}}}({\mathcal{M}}\boxtimes {\mathcal{N}}))&\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}}\boxtimes {\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \delta^{{-}1}(\mathrm{Sol}^\Lambda({\mathcal{M}})\boxtimes \mathrm{Sol}^\Lambda({\mathcal{N}}))[-\dim X]\nonumber\\ &\simeq \mathrm{Sol}^\Lambda({\mathcal{M}})\otimes \mathrm{Sol}^\Lambda({\mathcal{N}})[-\dim X], \end{align}

where we used Lemmas 4.20 and 8.10. This proves the first claim. The second claim follows from the adjunction.

Proposition 8.12 Let $f\colon X\rightarrow Y$. We have

(8.23)\begin{gather} \mathrm{Sol}^\Lambda\circ f^\star{\simeq} f^!\circ \mathrm{Sol}^\Lambda, \end{gather}

(8.24)\begin{gather}\mathrm{Sol}^\Lambda\circ {\mathbb{D}}\simeq {\mathbb{D}}\circ \mathrm{Sol}^\Lambda. \end{gather}

Proof. The first equation is followed by the second one and Proposition 8.9.

We have

(8.25)\begin{align} {\mathbb{D}}\circ \mathrm{Sol}^\Lambda({\mathcal{E}})&\simeq \mathop{{{\mathcal{H}}}om}\nolimits(\mathrm{Sol}^\Lambda({\mathcal{E}}), \omega^\Lambda_X)\nonumber\\ &\simeq M\circ \mathop{{{\mathcal{H}}}om}\nolimits^E(\mathrm{Sol}^E({\mathcal{E}}), \omega^E_X)\nonumber\\ &\simeq M\circ \mathrm{Sol}^E({\mathbb{D}}({\mathcal{E}}))\nonumber\\ &\simeq \mathrm{Sol}^\Lambda\circ {\mathbb{D}}({\mathcal{E}}), \end{align}

where we used Proposition 8.11 and the commutativity of $\mathrm {Sol}^E$ with ${\mathbb {D}}$ [DK16]. This completes the proof of the third line.

Proposition 8.13 Let $f\colon X\rightarrow Y$ be a proper map. Then we have

(8.26)\begin{equation} {\mathrm{DR}}^\Lambda\circ \int_{f!}\simeq f_!\circ {\mathrm{DR}}^\Lambda. \end{equation}

Proof. By various adjunctions, we have

(8.27)\begin{align} \operatorname{Hom}\bigg( {\mathrm{DR}}^\Lambda\bigg(\int_{f!}{\mathcal{M}}\bigg), {\mathrm{DR}}^\Lambda({\mathcal{N}})\bigg)&\cong \operatorname{Hom} \bigg(\int_{f!}{\mathcal{M}},{\mathcal{N}} \bigg)\nonumber\\ &\cong \operatorname{Hom}({\mathcal{M}}, f^{\dagger}{\mathcal{N}})\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), {\mathrm{DR}}^\Lambda(f^{\dagger}{\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}({\mathrm{DR}}^\Lambda({\mathcal{M}}), f^!{\mathrm{DR}}^\Lambda ({\mathcal{N}}))\nonumber\\ &\cong \operatorname{Hom}(f_!{\mathrm{DR}}^\Lambda({\mathcal{E}}), {\mathrm{DR}}^\Lambda {\mathcal{F}}). \end{align}

8.6 Corollaries

Proposition 8.14 Let $f\colon X\rightarrow Y$ be a proper morphism. Then $f_* {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.

Proof. For $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, take $ {\mathcal {V}}':= {\mathcal {V}}\otimes _\mathbb {k}{\mathbb {C}}$. We set ${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda })^{-1}( {\mathcal {V}}')$. Then $\int _{f!}{\mathbb {D}}{\mathcal {M}}$ is holonomic. Proposition 8.13 tells us ${\mathrm {DR}}^\Lambda (\int _{f!}{\mathbb {D}}{\mathcal {M}})\simeq f_!\circ {\mathrm {DR}}^\Lambda ({\mathbb {D}}\circ {\mathcal {M}})\simeq f_*\mathrm {Sol}^\Lambda ({\mathcal {M}})\simeq f_* {\mathcal {V}}'\otimes _\mathbb {k}{\mathbb {C}}$ is irregular constructible. Since the irregular constructibility is preserved under $\otimes _{\mathbb {k}}{\mathbb {C}}$. This completes the proof.

Remark 8.15 To work with more general base fields, it is desirable to have a direct proof of the above result, which we do not have yet.

The following proposition says ‘an object of $D^b_{ic}(\Lambda _X)$ is actually a sheaf over $X$.’ It is logically not important, but conceptually makes us feel easy with irregular constructible sheaves. We use some results from the later sections to prove the following.

Proposition 8.16 The essential image of $[\cdot ]\colon D^b(\mathrm {Mod}^0(\Lambda _X))\rightarrow D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ contains $D^b_{ic}(\Lambda _X)$.

Proof. Let $ {\mathcal {V}}$ be an irregular constructible sheaf. Then we have $[ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))]\simeq {\mathcal {V}}\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ by § 7.2 and Theorem 8.6. Since $[{\mathcal {E}}]\in D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _X))$ for ${\mathcal {E}}\in D^b(\mathrm {Ind}(\mathrm {Mod}^0(\Lambda _X)))$ if and only if ${\mathcal {E}}\in D^b(\mathrm {Mod}^0(\Lambda _X))$, we have $ {\mathbb {R}}\tilde {M}'(M^{-1}( {\mathcal {V}}))\in D^b(\mathrm {Mod}^0(\Lambda _X))$. This completes the proof.

9. Irregular perverse sheaves

In this section, we define the irregular perverse $t$-structure on the category of irregular constructible complexes. Over ${\mathbb {C}}$, the heart is equivalent to the category of holonomic ${\mathcal {D}}$-modules. We also prove $t$-exactness of various functors.

9.1 Irregular perverse sheaves

For an object $ {\mathcal {V}}$ of $D^b_{ic}(\Lambda _X)$, we define the support by

(9.1)\begin{equation} \mathrm{supp}({\mathcal{V}}):=\bigcup_{j}\mathrm{supp}({\mathfrak{F}}(H^j({\mathcal{V}}))) \subset X. \end{equation}

Let us define the irregular perverse $t$-structure.

Definition 9.1 Let ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ (respectively ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$) be the full subcategory of $D^b_{ic}(\Lambda _X)$ spanned by objects satisfying

(9.2)\begin{equation} \begin{array}{c} \dim\{\mathrm{supp}\, H^j({\mathcal{V}})\}\leqslant -j \\ (\text{respectively }\dim\{\mathrm{supp}\, H^j({\mathbb{D}}{\mathcal{V}})\}\leqslant -j ) \text{ for each }j\in {\mathbb{Z}}. \end{array} \end{equation}

Let $({^p}D^{\leqslant 0}(\mathbb {k}_X), {^p}D^{\geqslant 0}(\mathbb {k}_X))$ be the perverse $t$-structure of $D^b_c(\mathbb {k}_X)$.

Lemma 9.2 We have $ {\mathfrak {F}}({^p}D_{ic}^{\leqslant 0}(\Lambda _X))\subset {^p}D^{\leqslant 0}(\mathbb {k}_X)$. Conversely, if $ {\mathfrak {F}}( {\mathcal {V}})\in {^p}D^{\leqslant 0}(\mathbb {k}_X)$ for $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$, we have $ {\mathcal {V}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$.

Proof. Since $ {\mathfrak {F}}$ is $t$-exact with respect to the standard $t$-structure (Lemma 6.1), we have $H^i( {\mathfrak {F}}( {\mathcal {V}}))\cong {\mathfrak {F}}(H^i( {\mathcal {V}}))$.

Proposition 9.3 The pair $({^p}D_{ic}^{\leqslant 0}(\Lambda _X), {^p}D_{ic}^{\geqslant 0}(\Lambda _X))$ forms a $t$-structure.

To prove this proposition, we first prepare the following lemma.

Lemma 9.4 We have

(9.3)\begin{equation} H^ji_{(\bar{S}, D_S)}^{{-}1}{\mathcal{F}}\simeq 0 \text{ $(j>{-}\dim S)$ ,}\quad H^ji^!_{(\bar{S}, D_S)}{\mathcal{G}}\simeq 0 \text{ $(j<1-\dim S)$,} \end{equation}

for ${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$.

Proof. Note that the same statement for the usual perverse $t$-structure is known (e.g. [HTT08, Proposition 8.1.22]). By the commutativity proved in § 6, the first statement follows from Lemma 6.9. The second statement follows from the Verdier duality.

Proof Proof of Proposition 9.3

First, we will prove that for ${\mathcal {F}}\in {^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ${\mathcal {G}}\in {^p}D_{ic}^{\geqslant 1}(\Lambda _X)$, the vanishing

(9.4)\begin{equation} \operatorname{Hom}({\mathcal{F}}, {\mathcal{G}})=0. \end{equation}

One can prove this just by mimicking the proof of [KS90, Proposition 10.2.7].

It remains to show that there is a decomposition of objects in $D^b_{ic}(\Lambda _X)$. One can prove this by a usual argument for perverse sheaves as in [HTT08, Theorem 8.1.27].

Definition 9.5 The heart of the $t$-structure is called the category of irregular perverse sheaves and denoted by $\mathrm {Perv}_{ic}(k_X)$.

Theorem 9.6 The functor $\mathrm {Sol}^\Lambda$ restrict to a contravariant equivalence

(9.5)\begin{equation} \mathrm{Mod}_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\simeq} \mathrm{Perv}_{ic}({\mathbb{C}}_X). \end{equation}

Lemma 9.7 Let ${\mathcal {D}}_i$ $(i=1,2)$ be triangulated categories with $t$-structures $(D^{\leqslant 0}_i, D_i^{\geqslant 0})$. Let $F\colon {\mathcal {D}}_1\rightarrow {\mathcal {D}}_2$ be a $t$-exact equivalence. Then $F$ gives an equivalence between $t$-structures.

Proof. We have to show that $F\colon D^{\leqslant 0}_1\rightarrow D^{\leqslant 0}_2$ is essentially surjective. Let ${\mathcal {E}}$ be an object of $D^{\leqslant 0}_2$. Then we have a standard triangle

(9.6)\begin{equation} \tau_{\leqslant 0}F^{{-}1}({\mathcal{E}})\rightarrow F^{{-}1}({\mathcal{E}})\rightarrow \tau_{\geqslant 1}F^{{-}1}({\mathcal{E}})\xrightarrow{[1]}. \end{equation}

By applying $F$ again, we have $F(\tau _{\geqslant 1}F^{-1}({\mathcal {E}}))\cong 0$ since ${\mathcal {E}}\in D^{\leqslant 0}_2$. Since $F$ is an equivalence, we have $\tau _{\geqslant 1}F^{-1}({\mathcal {E}})\cong 0$. Hence $F^{-1}({\mathcal {E}})\in D^{\leqslant 0}_1$. We can prove for the positive part in a similar manner. This completes the proof.

Proof Proof of Theorem 9.6

By Lemma 9.7, it is enough to show that $\mathrm {Sol}^\Lambda$ is $t$-exact. We only show the condition

(9.7)\begin{equation} \dim \{\mathrm{supp}\, H^j(\mathrm{Sol}^\Lambda({\mathcal{M}}))\}\leqslant -j, \end{equation}

for any holonomic ${\mathcal {D}}$-module ${\mathcal {M}}$. The other case follows from the Verdier duality.

We will prove by induction on the dimension of the support of ${\mathcal {M}}$. Let $Z'$ be the support of ${\mathcal {M}}$ and $Z$ be the union of the component of the maximal dimension of $Z'$. Take $x\in Z$ and we will argue locally around $x$.

Take a divisor $D$ in $X$ such that $D$ does not contain any component of $Z$ but the singularities of ${\mathcal {M}}$. We set ${\mathcal {M}}_1:=\operatorname {im}({\mathcal {M}}\rightarrow {\mathcal {M}}(*D))$. Then we have two exact sequences

(9.8)\begin{equation} \begin{array}{c} 0\rightarrow {\mathcal{M}}_1\rightarrow {\mathcal{M}}(*D)\rightarrow C_0\rightarrow 0, \\ 0\rightarrow C_1\rightarrow {\mathcal{M}}\rightarrow {\mathcal{M}}_1\rightarrow 0. \end{array} \end{equation}

Since the supports of $C_0, C_1$ are in $D\cap Z$, the dimensions are less than $\dim Z$. By induction, (9.2) holds for $C_0, C_1$. Hence it suffices to show (9.2) for ${\mathcal {M}}(*D)$.

Let $p_1\colon (Z_1, D_1)\rightarrow (Z,D\cap Z)$ be a resolution of singularities of $(Z, D\cap Z)$ and $p_2$ be a proper modification given by Theorem 5.3 for $p_1^{\dagger} {\mathcal {M}}(*D)$. Then $p^{\dagger} {\mathcal {M}}(*D)$ ($p:=p_2\circ p_1$) satisfies (9.2), since its image under $\mathrm {Sol}^\Lambda$ is an irregular local system. Now we note the following inequalities:

(9.9)\begin{align} -j&\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda(p^{\dagger} {\mathcal{M}}(*D)))=\dim \mathrm{supp}\, {\mathcal{H}}^j(p^{{-}1}\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\nonumber\\ &=\dim \mathrm{supp}\, p^{{-}1}{\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D)))\geqslant \dim \mathrm{supp}\, {\mathcal{H}}^j(\mathrm{Sol}^\Lambda({\mathcal{M}}(*D))). \end{align}

This shows ${\mathcal {M}}(*D)$ also satisfies (9.2). This completes the proof.

We would like to make a comparison with usual perverse sheaves.

Proposition 9.8 We have $ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$, By Proposition 6.10, $ {\mathfrak {F}}\circ {\mathfrak {G}}=\operatorname {id}$ on $\mathrm {Perv}(X)$.

Proof. Since $ {\mathfrak {G}}$ is an exact functor, the condition in Definition 9.1 for $ {\mathfrak {G}}({\mathcal {E}})$ is equivalent to the condition for ${\mathcal {E}}$ to be a perverse sheaf. Hence we have $ {\mathfrak {G}}(\mathrm {Perv}(X))\subset \mathrm {Perv}_{ic}(X)$.

9.2 $t$-exactness of various operations

By using the functor $ {\mathfrak {F}}$, we can prove various $t$-exactness properties in parallel with the theory of usual perverse $t$-structure. We only discuss some of them for illustration.

Proposition 9.9 The Verdier duality functor ${\mathbb {D}}$ interchanges ${^p}D_{ic}^{\leqslant 0}(\Lambda _X)$ and ${^p}D_{ic}^{\geqslant 0}(\Lambda _X)$. In particular, ${\mathbb {D}}$ restricts to a contravariant autoequivalence of $\mathrm {Perv}_{ic}(\mathbb {k}_X)$.

Proof. Since ${\mathbb {D}}^2\cong \operatorname {id}$, the condition in Definition 9.1 for ${\mathbb {D}} {\mathcal {V}}$ is equivalent to that of $ {\mathcal {V}}$.

Proposition 9.10 Let $f\colon X\rightarrow Y$ be a morphism of complex manifolds. We assume that $f$ is proper for $3$ and $4$. The following hold.

1. (i) For any $ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _Y)$, we have $f^{-1} {\mathcal {V}}\in {^p}D_{ic}^{\leqslant \dim X-\dim Y}(\Lambda _X)$.

2. (ii) For any $ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _Y)$, we have $f^{!} {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _X)$.

3. (iii) For any $ {\mathcal {V}}\in {^p}D^{\geqslant 0}_{ic}(\Lambda _X)$, we have $ {\mathbb {R}} f_* {\mathcal {V}}\in {^p}D_{ic}^{\geqslant -\dim X+\dim Y}(\Lambda _Y)$.

4. (iv) For any $ {\mathcal {V}}\in {^p}D^{\leqslant 0}_{ic}(\Lambda _X)$, we have $ {\mathbb {R}} f_! {\mathcal {V}}\in {^p}D_{ic}^{\leqslant (\dim X-\dim Y)}(\Lambda _Y)$.

Proof. The statements (i), (iii) and (iv) can also be proved easily by using the commutativities of $ {\mathfrak {F}}$ with $f^{-1}$ and $f_!$ (§ 6) and Lemma 9.2. The statement (ii) is the Verdier dual of (i).

Remark 9.11 Other right/left $t$-exactness for various functors known in the theory of perverse sheaves can be also proved by using the argument used in Proposition 9.10.

Remark 9.12 Here we assumed the properness for (iii) and (iv) for simplicity. One can remove the assumption by working with ind/pro objects to define push-forwards for nontame morphisms.

10. Algebraic case

In this section, we deduce the algebraic version of the results.

10.1 Notation for algebraic ${\mathcal {D}}$-modules

For the theory of algebraic ${\mathcal {D}}$-modules, we refer to [HTT08]. For a smooth quasi-projective variety $X$, we denote the sheaf of algebraic differential operators by ${\mathcal {D}}_X$. We denote the category of left ${\mathcal {D}}_X$-modules by $\mathrm {Mod}({\mathcal {D}}_X)$, the bounded derived category by $D^b({\mathcal {D}}_X)$, and the full subcategory of cohomologically holonomic modules by $D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.

We denote the Verdier duality functor by ${\mathbb {D}}$. For a morphism of algebraic varieties $f\colon X\rightarrow Y$, we define $\int _f$ and $f^{\dagger}$ by the same formula as in the analytic case. In the algebraic case, both functors preserve holonomic objects without properness assumption. We set $f^\star :={\mathbb {D}}\circ f^{\dagger} \circ {\mathbb {D}}$ and $\int _{f!}:={\mathbb {D}}\circ \int _f\circ {\mathbb {D}}$. Then we have two adjoint pairs $f^\star \dashv \int _f$ and $\int _{f!}\dashv f^{\dagger}$.

Let $X^{{\mathrm {an}}}$ be the complex manifold associated with $X$. The analytification functor is an exact functor $(\cdot )^{{\mathrm {an}}} \colon \mathrm {Mod}({\mathcal {D}}_X)\rightarrow \mathrm {Mod}({\mathcal {D}}_{X^{{\mathrm {an}}}})$. We also denote the induced functor on the derived categories by the same notation $(\cdot )^{\mathrm {an}}$. It preserves the holonomicity. We note the following.

Lemma 10.1 [HTT08, Proposition 4.7.2]

Let $f\colon X\rightarrow Y$ be a morphism between algebraic varieties and $f^{{\mathrm {an}}}\colon X^{{\mathrm {an}}}\rightarrow Y^{{\mathrm {an}}}$ be the associated morphisms between complex manifolds. Then the following hold.

1. (i) For ${\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_Y)$, we have a canonical isomorphism $(f^{\dagger} {\mathcal {M}})^{{\mathrm {an}}}\simeq (f^{{\mathrm {an}}})^{\dagger} ({\mathcal {M}})^{{\mathrm {an}}}$.

2. (ii) If $f$ is proper, we have a canonical isomorphism $\big (\int _f{\mathcal {N}}\big )^{\mathrm {an}} \simeq \int _{f^{\mathrm {an}}}({\mathcal {N}})^{\mathrm {an}}$ for ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$.

10.2 Algebraic irregular constructible sheaves

To consider irregular constructible sheaves, we will equip quasi-projective algebraic varieties with analytic topology. Let $X$ be a smooth quasi-projective variety. Let ${\bar {X}}$ be a smooth projective variety with a Zariski open embedding $i_X\colon X\rightarrow {\bar {X}}$. We set $j_{X}\colon D_X:={\bar {X}}{\backslash } X\hookrightarrow X$.

Definition 10.2 An object $ {\mathcal {V}}\in \mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$ is algebraic irregular constructible if the following holds: there exists an algebraic stratification ${\mathcal {S}}$ of ${\bar {X}}$ refining ${\bar {X}}=X\sqcup D_X$ such that each restriction of $ {\mathcal {V}}$ to $S\in {\mathcal {S}}$ is an irregular local system.

We denote the full subcategory of irregular constructible sheaves by $\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$. Let $i_{({\bar {X}}, D_X)}\colon {({\bar {X}}, D_X)}\rightarrow ({\bar {X}},\varnothing )$ be the canonical morphism, which is tame. We also denote the inclusion by $i_{D_X}\colon (D_X,\varnothing )\rightarrow ({\bar {X}}, \varnothing )$. The functors $i_{{({\bar {X}}, D_X)}!}, i_{{({\bar {X}}, D_X)}*}$ are fully faithful by Lemma 5.40.

Lemma 10.3 The category $\mathrm {Mod}_{ic}(\Lambda _{({\bar {X}}, D_X)})$ does not depend on the choice of ${\bar {X}}$.

Proof. We will prove the assertion in two steps. Let us first assume that $p\colon {\bar {X}}'\rightarrow {\bar {X}}$ is a map between two projective compactifications of $X$ extending $\operatorname {id}\colon X\rightarrow X$. Then it is clear that $p_*$ induces the desired equivalence of categories.

Now let ${\bar {X}}'$ be an arbitrary projective compactification of $X$. Then there exists ${\bar {X}}''$ with maps ${\bar {X}}''\rightarrow {\bar {X}}$ and ${\bar {X}}''\rightarrow {\bar {X}}'$ extending $\operatorname {id} \colon X\rightarrow X$. This can be done by taking a smooth blow-up replacement of the closure of the diagonal embedding $X\rightarrow {\bar {X}}\times {\bar {X}}'$. From the first part of this proof, we complete the proof.

We will denote the category of algebraic irregular constructible sheaves by $\mathrm {Mod}_{ic}(\Lambda _X)$.

Lemma 10.4 The abelian subcategory $\mathrm {Mod}_{ic}(\Lambda _X)$ is thick in $\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)})$.

Proof. One can prove the lemma by mimicking the proof of Lemma 5.28.

Let us denote the triangulated subcategory of $D^b(\mathrm {Mod}^{\mathfrak {I}}(\Lambda _{({\bar {X}}, D_X)}))$ formed by cohomologically algebraic irregular constructible sheaves by $D^{b}_{ic}(\Lambda _X)$.

Let $D^{b}_c(\mathbb {k}_X)$ be the category of cohomologically algebraic constructible complexes.

Proposition 10.5 The functor $ {\mathfrak {F}}$ restricts to a functor $ {\mathfrak {F}}\colon D^{b}_{ic}(\Lambda _X)\rightarrow D^{b}_c(\mathbb {k}_X)$.

Proof. The proof of proposition 6.7 works for this case.

It is also clear that the results we proved in § 5.4 also hold for $D^{b}(\Lambda _X)$. In addition to these, we have the following.

Let $f\colon X\rightarrow Y$ be a morphism between algebraic varieties. There exist compactifications $\bar {X},\bar {Y}$ such that $f$ admits an extension $f\colon \bar {X}\rightarrow \bar {Y}$. Hence, considering the analytic topology, $f$ extends as a map $f\colon (\bar {X}, D_X)\rightarrow (\bar {Y}, D_Y)$. We set

(10.1)\begin{equation} \begin{gathered} f_*:=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_*i_{{({\bar{X}}, D_X)}*}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})),\\ f_! :=i_{({\bar{Y}}, D_Y)}^{{-}1}\circ f_!i_{{({\bar{X}}, D_X)}!}\colon D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{X}}, D_X)}))\rightarrow D^b(\mathrm{Mod}^{\mathfrak{I}}(\Lambda_{({\bar{Y}}, D_Y)})). \end{gathered} \end{equation}

Proposition 10.6 Let $f\colon X\rightarrow Y$ be a morphism between algebraic varieties. Then $f_* {\mathcal {V}}, f_! {\mathcal {V}}\in D^b_{ic}(\Lambda _Y)$ for $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$.

Proof. This can be proved by the same argument used in Proposition 8.14 by using Proposition 10.10.

10.3 Algebraic Riemann–Hilbert correspondence

We first recall the following result due to Malgrange.

Theorem 10.7 [Mal04]

If $X$ is a smooth projective variety, analytic holonomic ${\mathcal {D}}_X$-modules are algebraic.

By using this, we have the following algebraic version of irregular Riemann–Hilbert correspondence.

Theorem 10.8 There exists an exact equivalence

(10.2)\begin{equation} \mathrm{Sol}^\Lambda_X\colon D^b_{\mathrm{hol}}({\mathcal{D}}_X)\xrightarrow{\cong} D^{b}_{ic}(\Lambda_X). \end{equation}

Proof. If $X$ is projective, there is nothing to prove by Theorem 10.7. We suppose $X$ is quasi-projective and $\bar {X}$ be a compactification of $X$. For ${\mathcal {M}}\in D^{b}_{\mathrm {hol}}({\mathcal {D}}_X)$, we have $\int _{i_X}{\mathcal {M}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_{\bar {X}})$ where $i_X\colon X\hookrightarrow {\bar {X}}$ is the inclusion. Then we get a functor

(10.3)\begin{align} \mathrm{Sol}^\Lambda_X&:= i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ({\cdot})^{{\mathrm{an}}} \circ\int_{i_X}\colon D^b_\mathrm{hol}({\mathcal{D}}_X)\rightarrow D^{b}_{ic}(\Lambda_{{\bar{X}}^{\mathrm{an}}})\nonumber\\ &= D^b_{ic}(\Lambda_{\bar{X}})\xrightarrow{i_{({\bar{X}}, D_X)}^{{-}1}} D^b_{ic}(\Lambda_{({\bar{X}}, D_X)}). \end{align}

The middle equality is Chow's lemma. Note that the first three compositions are fully faithful.

Hence, to prove the full faithfulness of $\mathrm {Sol}^\Lambda _X$, it suffices to show that the image of $\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}\circ (\cdot )^{{\mathrm {an}}} \circ \int _{i_X}$ is zero under $i_{D_X}^{-1}$ by Lemma 5.40. Let ${\mathcal {S}}$ be a stratification of $D_X$ such that each stratum is smooth. For $S\in {\mathcal {S}}$, we have $i_S^{{\dagger} }(\int _{i_X}{\mathcal {M}})\simeq 0$ where $i_S\colon S\hookrightarrow {\bar {X}}$ is the inclusion. Hence we have

(10.4)\begin{align} i_S^{{-}1}\mathrm{Sol}^{\Lambda}_X({\mathcal{M}})&\simeq i_S^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{{\mathrm{an}}}\circ \int_{i_X}{\mathcal{M}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ i_{S}^{{{\dagger}}}\circ \bigg(\int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\nonumber\\ &\simeq \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ \bigg( i_{S}^{{{\dagger}}}\circ \int_{i_X}{\mathcal{M}}\bigg)^{\mathrm{an}}\simeq 0. \end{align}

Hence we can conclude that $i_{D_X}^{-1}\mathrm {Sol}^\Lambda _{{\bar {X}}^{\mathrm {an}}}({\mathcal {M}})\simeq 0$. Then the full faithfulness of $\mathrm {Sol}^\Lambda _X$ is evident from Lemma 5.40.

To see the essential surjectivity, let us take an object $ {\mathcal {V}}\in D^b_{ic}(\Lambda _X)$ and consider it as an object of $D^b_{ic}(\Lambda _{\bar {X}})=D^b_{ic}(\Lambda _{{\bar {X}}^{\mathrm {an}}})$. Then we have ${\mathcal {M}}:=(\mathrm {Sol}^{\Lambda }_{{\bar {X}}^{{\mathrm {an}}}})^{-1}( {\mathcal {V}})\in D^b_{\mathrm {hol}}({\mathcal {D}}_{{\bar {X}}^{\mathrm {an}}})$. We set ${\mathcal {M}}^\mathrm {alg}:=((\cdot )^{\mathrm {an}})^{-1}({\mathcal {M}})$. Take a stratification ${\mathcal {S}}$ of $D_X$ with smooth strata. To prove ${\mathcal {M}}^\mathrm {alg}$ is isomorphic to $\int _{i_X}{\mathcal {N}}$ for ${\mathcal {N}}\in D^b_{\mathrm {hol}}({\mathcal {D}}_X)$, it is enough to see $i_S^{{\dagger} }{\mathcal {M}}^{\mathrm {alg}}\simeq 0$ for each $S\in {\mathcal {S}}$. Note that $i_S^{\dagger} {\mathcal {M}}^\mathrm {alg}\simeq 0$ is equivalent to $(i_S^{\dagger} {\mathcal {M}}^\mathrm {alg})^{an}\simeq 0$. The latter can be shown as follows:

(10.5)\begin{align} \mathrm{Sol}_{S^{\mathrm{an}}}^\Lambda(i_S^{\dagger}{\mathcal{M}}^\mathrm{alg})^{{\mathrm{an}}}&\simeq \mathrm{Sol}^\Lambda_{S^{\mathrm{an}}}(i_{S^{\mathrm{an}}}^{\dagger}{\mathcal{M}}) \nonumber\\ &\simeq i_S^{{-}1}\mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}({\mathcal{M}})\nonumber\\ &\simeq i_S^{{-}1}{\mathcal{V}}\simeq 0. \end{align}

This completes the proof.

For the next subsection, we also prepare the following: we set ${\mathrm {DR}}^\Lambda _X:={\mathbb {D}}_{{({\bar {X}}, D_X)}}\circ \mathrm {Sol}^\Lambda _X$, which is an equivalence.

Lemma 10.9 There exist isomorphisms

(10.6)\begin{equation} {\mathrm{DR}}^\Lambda_X\simeq i_{{({\bar{X}}, D_X)}}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ \int_{i_X}\simeq i_{({\bar{X}}, D_X)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ \int_{i_X!}. \end{equation}

Proof. We have

(10.7)\begin{align} {\mathrm{DR}}^\Lambda_X&\simeq {\mathbb{D}}_{{({\bar{X}}, D_X)}}\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ\int_{i_X}\nonumber\\ &\simeq i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathbb{D}}_{\bar{X}}\circ \mathrm{Sol}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ\int_{i_X}\nonumber\\ &=i^{{-}1}_{({\bar{X}}, D_X)}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X}.\end{align}

10.4 Comparisons of the functors

Let $X, Y$ be smooth quasi-projective varieties and $f\colon X\rightarrow Y$ be a morphism. Recall that holonomicity of algebraic ${\mathcal {D}}$-modules is preserved by the six operations.

Proposition 10.10 There exist canonical isomorphisms:

(10.8)\begin{gather} f_*\circ {\mathrm{DR}}_X^\Lambda\simeq {\mathrm{DR}}^\Lambda_Y\circ \int_{f}, \end{gather}

(10.9)\begin{gather}f_!\circ {\mathrm{DR}}_X^\Lambda\simeq {\mathrm{DR}}_Y^\Lambda \circ \int_{f!}, \end{gather}

(10.10)\begin{gather}f^{{-}1}\circ {\mathrm{DR}}_Y^\Lambda\simeq {\mathrm{DR}}_X^\Lambda\circ f^\star , \end{gather}

(10.11)\begin{gather}f^!\circ {\mathrm{DR}}_Y^\Lambda\simeq {\mathrm{DR}}_X^\Lambda\circ f^{\dagger}. \end{gather}

Proof. The third and fourth lines follow from the analytic cases. To prove the first and second lines, let us take a projective compactification $i_X\colon X\hookrightarrow {\bar {X}}$ and $i_Y\colon Y\hookrightarrow {\bar {Y}}$ and a map $\bar {f}\colon {\bar {X}}\rightarrow {\bar {Y}}$ extending $f$. We have

(10.12)\begin{align} {\mathrm{DR}}^\Lambda_Y\circ \int_{f!} &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_Y!}\circ \int_{f!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{\bar{f}}\circ \int_{i_X!}\nonumber\\ &\simeq i_{({\bar{Y}}, D_Y)}^{{-}1}\circ \bar{f}_!\circ {\mathrm{DR}}^\Lambda_{{\bar{Y}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}} \circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ i_{({\bar{X}}, D_X)}^{{-}1}\circ {\mathrm{DR}}^\Lambda_{{\bar{X}}^{\mathrm{an}}}\circ ({\cdot})^{\mathrm{an}}\circ \int_{i_X!}\nonumber\\ &\simeq f_!\circ {\mathrm{DR}}^\Lambda_X. \end{align}

By using Lemma 10.9, one can prove the first formula in the same way.

10.5 Algebraic irregular perverse sheaves

In the same way as in Definition 9.1, we define $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ on $D^{b}_{ic}(\Lambda _X)$.

Proposition 10.11 The following hold.

1. (i) The pair $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ forms a $t$-structure on $D^{b}_{ic}(\Lambda _X)$.

2. (ii) The heart $\mathrm {Perv}_{ic}(k_X)$ of the $t$-structure $({^p}D^{\leqslant 0}_{ic}(\Lambda _X), {^p}D^{\geqslant 0}_{ic}(\Lambda _X))$ is equivalent to $\mathrm {Mod}_{\mathrm {hol}}({\mathcal {D}}_X)$ under the Riemann–Hilbert correspondence (Theorem 10.8).

3. (iii) The heart $\mathrm {Perv}_{ic}(\mathbb {k}_X)$ is stable under the Verdier duality. The $t$-exactness in Proposition 9.10 also holds in this setting without the properness assumption.

Proof. One can prove this in the same way as in the analytic setting except for nonproper setting of (iii). Let $f$ be a morphism $X\rightarrow Y$ and a compactification ${\bar {X}}\rightarrow {\bar {Y}}$. Then we have

(10.13)\begin{equation} {\mathfrak{F}}\circ f_!:={\mathfrak{F}}\circ \bar{f}_!\circ i_{{({\bar{X}}, D_X)}!}\simeq \bar{f}_!\circ i_{X!}\circ {\mathfrak{F}}\simeq f_!\circ {\mathfrak{F}} \end{equation}

by Lemmas 6.5 and 6.6. This proves the desired statement for $f_!$. The statement for $f_*$ is obtained by taking the Verdier dual.