Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-03T22:05:56.709Z Has data issue: false hasContentIssue false
  • English
  • Français

Hecke category actions via Smith–Treumann theory

Part of: Linear algebraic groups and related topics

Published online by Cambridge University Press:  23 August 2023

J. Ciappara
J. Ciappara*
Affiliation:
School of Mathematics and Statistics F07, University of Sydney, NSW 2006, Australia [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 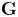$\textbf {G}$ be a simply connected semisimple algebraic group over a field of characteristic greater than the Coxeter number. We construct a monoidal action of the diagrammatic Hecke category on the principal block 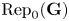$\operatorname {Rep}_0(\textbf {G})$ of 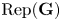$\operatorname {Rep}(\textbf {G})$ by wall-crossing functors. This action was conjectured to exist by Riche and Williamson. Our method uses constructible sheaves and relies on Smith–Treumann theory.

Keywords

algebraic groupsrepresentationsconstructible sheavesHecke category

MSC classification

Primary: 20G05: Representation theory
Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 10 , October 2023 , pp. 2089 - 2124
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N., A bimodule description of the Hecke category, Compos. Math. 157 (2021), 2133–2159.CrossRefGoogle Scholar
Achar, P. N., Perverse sheaves and applications to representation theory, Mathematical Surveys and Monographs (American Mathematical Society, 2021).CrossRefGoogle Scholar
Achar, P. N., Makisumi, S., Riche, S. and Williamson, G., Koszul duality for Kac–Moody groups and characters of tilting modules, J. Amer. Math. Soc. 32 (2019), 261–310.10.1090/jams/905CrossRefGoogle Scholar
Achar, P. and Riche, S., Reductive groups, the loop Grassmannian, and the Springer resolution, Invent. Math. 214 (2018), 289–436.10.1007/s00222-018-0805-1CrossRefGoogle Scholar
Andersen, H. H., Jantzen, J. C. and Soergel, W., Representations of quantum groups at a $p$th root of unity and of semisimple groups in characteristic $p$: independence of $p$, Astérisque 220 (1994).Google Scholar
Baumann, P. and Riche, S., Notes on the geometric Satake equivalence, in Relative aspects in representation theory, Langlands functoriality and automorphic forms: CIRM Jean-Morlet Chair, Spring 2016, eds Heiermann, V. and Prasad, D. (Springer, 2018), 1–134.Google Scholar
Bernstein, J. and Lunts, V., Equivariant sheaves and functors (Springer, 2006).Google Scholar
Bezrukavnikov, R., Gaitsgory, D., Mirković, I., Riche, S. and Rider, L., An Iwahori–Whittaker model for the Satake category, J. Éc. polytech. Math. 6 (2019), 707–735.CrossRefGoogle Scholar
Bezrukavnikov, R. and Riche, S., Hecke action on the principal block, Compos. Math. 158 (2022), 953–1019.CrossRefGoogle Scholar
Bezrukavnikov, R. and Yun, Z., On Koszul duality for Kac–Moody groups, Represent. Theory 17 (2013), 1–98.10.1090/S1088-4165-2013-00421-1CrossRefGoogle Scholar
Borceux, F., Handbook of categorical algebra, Encyclopedia of Mathematics and its Applications, vol. 1 (Cambridge University Press, 1994).Google Scholar
Brylinski, J.-L., Loop spaces, characteristic classes and geometric quantization, Modern Birkhäuser Classics (Birkhäuser, 1993).CrossRefGoogle Scholar
Cline, E., Parshall, B. and Scott, L., Finite dimensional algebras and highest weight categories, J. Reine Angew. Math. 391 (1988), 85–99.Google Scholar
Danilov, V. I., Iskovskikh, V. A., Shafarevich, I. R. and Treger, R., Algebraic geometry II: cohomology of algebraic varieties. Algebraic surfaces, Encyclopaedia of Mathematical Sciences (Springer, 2013).Google Scholar
de Cataldo, M. A. A. and Migliorini, L., The decomposition theorem, perverse sheaves and the topology of algebraic maps, Bull. Amer. Math. Soc. (N.S.) 46 (2009), 535–633.CrossRefGoogle Scholar
Elias, B., Makisumi, S., Thiel, U. and Williamson, G., An introduction to Soergel bimodules (Springer, 2020).CrossRefGoogle Scholar
Elias, B. and Williamson, G., Soergel calculus, Represent. Theory 20 (2016), 295–374.10.1090/ert/481CrossRefGoogle Scholar
Görtz, U., Affine Springer fibers and affine Deligne–Lusztig varieties, in Affine flag manifolds and principal bundles, ed. Schmitt, A. (Springer, 2010), 1–50.Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-modules, perverse sheaves, and representation theory, Progress in Mathematics (Birkhäuser, 2007).Google Scholar
Jantzen, J. C., Representations of algebraic groups (American Mathematical Society, 2003).Google Scholar
Juteau, D., Mautner, C. and Williamson, G., Perverse sheaves and modular representation theory, Sémin. Congr. 24 (2012), 313–350.Google Scholar
Krause, H., Krull–Schmidt categories and projective covers, Expo. Math. 33 (2015), 535–549.CrossRefGoogle Scholar
Kumar, S., Kac–Moody groups, their flag varieties and representation theory, Progress in Mathematics (Birkhäuser, 2002).CrossRefGoogle Scholar
Le, J. and Chen, X., Karoubianness of a triangulated category, J. Algebra 310 (2007), 452–457.CrossRefGoogle Scholar
Leslie, S. and Lonergan, G., Parity sheaves and Smith theory, J. Reine Angew. Math. 2021 (2021), 49–87.CrossRefGoogle Scholar
Libedinsky, N. and Williamson, G., The anti-spherical category, Adv. Math. 405 (2022), 108509.CrossRefGoogle Scholar
Mathieu, O., Formules de caractères pour les algèbres de Kac–Moody générales, Astérisque 159–160 (1988).Google Scholar
Mautner, C. and Riche, S., Exotic tilting sheaves, parity sheaves on affine Grassmannians, and the Mirković–Vilonen conjecture, J. Eur. Math. Soc. (JEMS) 20 (2018), 2259–2332.CrossRefGoogle Scholar
Mirković, I. and Vilonen, K., Geometric Langlands duality and representations of algebraic groups over commutative rings, Ann. of Math. (2) 166 (2007), 95–143.CrossRefGoogle Scholar
Nadler, D., Perverse sheaves on real loop Grassmannians, Invent. Math. 159 (2004), 1–73.CrossRefGoogle Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, vol. 148 (Princeton University Press, 2014).Google Scholar
nLab authors. Recollement, http://ncatlab.org/nlab/show/recollement, Revision 17 (December 2020).Google Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their affine flag varieties, Adv. Math. 219 (2008), 118–198.CrossRefGoogle Scholar
Riche, S., Geometric representation theory in positive characteristic, Habilitation à diriger des recherches, Université Blaise Pascal (Clermont Ferrand 2) (2016).Google Scholar
Riche, S. and Williamson, G., Tilting modules and the $p$-canonical basis, Astérisque 397 (2018).CrossRefGoogle Scholar
Riche, S. and Williamson, G., Smith–Treumann theory and the linkage principle, Publ. Math. Inst. Hautes Études Sci. 136 (2022), 225–292.CrossRefGoogle Scholar
The Stacks Project Authors, The Stacks project (2021), https://stacks.math.columbia.edu.Google Scholar
Stalder, N., Scalar extension of Abelian and Tannakian categories, Preprint (2018), arXiv0806.0308.Google Scholar
Treumann, D., Smith theory and geometric Hecke algebras, Math. Ann. 375 (2019), 595–628.CrossRefGoogle Scholar
Waschkies, I., The stack of microlocal perverse sheaves, Bull. Soc. Math. France 132 (2004), 397–462.CrossRefGoogle Scholar
Weidner, J., Modular equivariant formality, Preprint (2013), arXiv:1312.4776.Google Scholar
Williamson, G., Schubert calculus and torsion explosion, J. Amer. Math. Soc. 30 (2017), 1023–1046.CrossRefGoogle Scholar
Zhu, X., An introduction to affine Grassmannians and the geometric Satake equivalence, Geom. Moduli Spaces Represent. Theory 24 (2017), 59–154.CrossRefGoogle Scholar