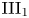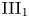1. Introduction
Let ![]() $M$ be a von Neumann algebra and
$M$ be a von Neumann algebra and ![]() $\operatorname {Aut}(M)$ the set of all automorphisms on
$\operatorname {Aut}(M)$ the set of all automorphisms on ![]() $M$. We say that
$M$. We say that ![]() $\theta \in \operatorname {Aut}(M)$ is pointwise inner [Reference Haagerup and StørmerHS87] if for each positive linear functional
$\theta \in \operatorname {Aut}(M)$ is pointwise inner [Reference Haagerup and StørmerHS87] if for each positive linear functional ![]() $\varphi \in M_*^+$, there is a unitary
$\varphi \in M_*^+$, there is a unitary ![]() $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that ![]() $\theta (\varphi )=u\varphi u^*$, where we used the notation
$\theta (\varphi )=u\varphi u^*$, where we used the notation ![]() $\theta (\varphi ):=\varphi \circ \theta ^{-1}$ and
$\theta (\varphi ):=\varphi \circ \theta ^{-1}$ and ![]() $x\varphi y := \varphi (y \, \cdot \, x)$ for
$x\varphi y := \varphi (y \, \cdot \, x)$ for ![]() $x,y\in M$. In other words,
$x,y\in M$. In other words, ![]() $\theta$ is pointwise inner if the induced map
$\theta$ is pointwise inner if the induced map ![]() $\theta \colon M_\ast ^+ \to M_\ast ^+$ is inner at a pointwise level. This notion naturally appeared in the study of unitary equivalence relations on state spaces on von Neumann algebras and was intensively studied by Haagerup and Størmer [Reference Haagerup and StørmerHS87, Reference Haagerup and StørmerHS88, Reference Haagerup and StørmerHS91].
$\theta \colon M_\ast ^+ \to M_\ast ^+$ is inner at a pointwise level. This notion naturally appeared in the study of unitary equivalence relations on state spaces on von Neumann algebras and was intensively studied by Haagerup and Størmer [Reference Haagerup and StørmerHS87, Reference Haagerup and StørmerHS88, Reference Haagerup and StørmerHS91].
Any inner automorphism is pointwise inner. Indeed, we can choose the same unitary for all elements in ![]() $M_\ast ^+$. A nontrivial and motivating example comes from Tomita–Takesaki modular theory, that is, every modular automorphism
$M_\ast ^+$. A nontrivial and motivating example comes from Tomita–Takesaki modular theory, that is, every modular automorphism ![]() $\sigma _t^\varphi$ is pointwise inner, where
$\sigma _t^\varphi$ is pointwise inner, where ![]() $\varphi \in M_\ast ^+$ is a faithful state and
$\varphi \in M_\ast ^+$ is a faithful state and ![]() $t\in \mathbb {R}$; see § 2. Hence, every composition
$t\in \mathbb {R}$; see § 2. Hence, every composition ![]() $\operatorname {Ad}(u)\circ \sigma ^\varphi _t$ of an inner and a modular automorphism is pointwise inner because the pointwise inner property is closed under compositions. Haagerup and Størmer conjectured that the opposite phenomenon also holds for every type
$\operatorname {Ad}(u)\circ \sigma ^\varphi _t$ of an inner and a modular automorphism is pointwise inner because the pointwise inner property is closed under compositions. Haagerup and Størmer conjectured that the opposite phenomenon also holds for every type ![]() ${\rm III_1}$ factor [Reference Haagerup and StørmerHS88].
${\rm III_1}$ factor [Reference Haagerup and StørmerHS88].
Haagerup–Størmer conjecture Let ![]() $M$ be a type
$M$ be a type ![]() ${\rm III_1}$ factor with separable predual. Then every pointwise inner automorphism is a composition of an inner and a modular automorphism.
${\rm III_1}$ factor with separable predual. Then every pointwise inner automorphism is a composition of an inner and a modular automorphism.
We note that if ![]() $M$ is a factor that is not of type
$M$ is a factor that is not of type ![]() ${\rm III_1}$, similar results were obtained in [Reference Haagerup and StørmerHS87, Reference Haagerup and StørmerHS88], hence the only remaining problem for characterizing pointwise inner automorphisms is the case for type
${\rm III_1}$, similar results were obtained in [Reference Haagerup and StørmerHS87, Reference Haagerup and StørmerHS88], hence the only remaining problem for characterizing pointwise inner automorphisms is the case for type ![]() ${\rm III_1}$ factors. We also note that the separability assumption is necessary; see [Reference Haagerup and StørmerHS88, § 6] and [Reference Ando and HaagerupAH12, Remark 4.21].
${\rm III_1}$ factors. We also note that the separability assumption is necessary; see [Reference Haagerup and StørmerHS88, § 6] and [Reference Ando and HaagerupAH12, Remark 4.21].
In the present paper, we give a partial but satisfactory answer to this conjecture. To explain it, we prepare some terminology. For an inclusion of von Neumann algebras ![]() $N\subset M$, we say it is irreducible if
$N\subset M$, we say it is irreducible if ![]() $N'\cap M \subset N$, and is with expectation if there exists a faithful normal conditional expectation from
$N'\cap M \subset N$, and is with expectation if there exists a faithful normal conditional expectation from ![]() $M$ onto
$M$ onto ![]() $N$. For every faithful state, or more generally, every faithful semifinite normal weight,
$N$. For every faithful state, or more generally, every faithful semifinite normal weight, ![]() $\varphi$ on
$\varphi$ on ![]() $M$, we denote by
$M$, we denote by ![]() $M_\varphi$ the centralizer of
$M_\varphi$ the centralizer of ![]() $\varphi$, which is the fixed point algebra of
$\varphi$, which is the fixed point algebra of ![]() $\sigma ^\varphi$. When
$\sigma ^\varphi$. When ![]() $M$ is a type
$M$ is a type ![]() ${\rm III_1}$ factor with separable predual, the existence of a faithful state
${\rm III_1}$ factor with separable predual, the existence of a faithful state ![]() $\varphi \in M_\ast$ with
$\varphi \in M_\ast$ with ![]() $M_\varphi '\cap M=\mathbb {C}$ is equivalent to having trivial bicentralizer; see § 2. In this case,
$M_\varphi '\cap M=\mathbb {C}$ is equivalent to having trivial bicentralizer; see § 2. In this case, ![]() $M_\varphi \subset M$ is an irreducible subfactor of type
$M_\varphi \subset M$ is an irreducible subfactor of type ![]() ${\rm II_1}$ with expectation, and the existence of such a subfactor is very useful in many contexts. Connes’ bicentralizer problem, which is one of the most important problems for type
${\rm II_1}$ with expectation, and the existence of such a subfactor is very useful in many contexts. Connes’ bicentralizer problem, which is one of the most important problems for type ![]() ${\rm III}$ factors, asks if every type
${\rm III}$ factors, asks if every type ![]() ${\rm III_1}$ factor with separable predual has trivial bicentralizer. To the best of our knowledge, all concrete examples of type
${\rm III_1}$ factor with separable predual has trivial bicentralizer. To the best of our knowledge, all concrete examples of type ![]() ${\rm III_1}$ factors have trivial bicentralizers. Further, if
${\rm III_1}$ factors have trivial bicentralizers. Further, if ![]() $M$ is a type
$M$ is a type ![]() ${\rm III_1}$ factor, then the tensor product
${\rm III_1}$ factor, then the tensor product ![]() $M\mathbin {\overline {\otimes }} R_\infty$ has trivial bicentralizer, where
$M\mathbin {\overline {\otimes }} R_\infty$ has trivial bicentralizer, where ![]() $R_\infty$ is the Araki–Woods factor of type
$R_\infty$ is the Araki–Woods factor of type ![]() ${\rm III_1}$ [Reference MarrakchiMar18].
${\rm III_1}$ [Reference MarrakchiMar18].
We now introduce our main theorem. For objects in (3) below; see § 2.
Theorem A. Let ![]() $M$ be a type
$M$ be a type ![]() ${\rm III_1}$ factor with separable predual and assume it has trivial bicentralizer. Fix a faithful state
${\rm III_1}$ factor with separable predual and assume it has trivial bicentralizer. Fix a faithful state ![]() $\varphi \in M_\ast$ such that
$\varphi \in M_\ast$ such that ![]() $M_\varphi '\cap M=\mathbb {C}$. Then for each
$M_\varphi '\cap M=\mathbb {C}$. Then for each ![]() $\theta \in \operatorname {Aut}(M)$, the following conditions are equivalent.
$\theta \in \operatorname {Aut}(M)$, the following conditions are equivalent.
(1) The automorphism
 $\theta$ is pointwise inner.
$\theta$ is pointwise inner.(2) For each faithful state
 $\psi \in M_\ast$ with
$\psi \in M_\ast$ with  $M_\psi '\cap M =\mathbb {C}$, there exists
$M_\psi '\cap M =\mathbb {C}$, there exists  $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that  $\theta (x) = uxu^*$ for all
$\theta (x) = uxu^*$ for all  $x\in M_\psi$.
$x\in M_\psi$.(3) There exists
 $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that  $\theta ^\omega (x)=uxu^*$ for all
$\theta ^\omega (x)=uxu^*$ for all  $x\in (M^\omega )_{\varphi ^\omega }$, where
$x\in (M^\omega )_{\varphi ^\omega }$, where  $\omega$ is a fixed free ultrafilter on
$\omega$ is a fixed free ultrafilter on  $\mathbb {N}$.
$\mathbb {N}$.(4) There exist
 $u\in \mathcal {U}(M)$ and
$u\in \mathcal {U}(M)$ and  $t\in \mathbb {R}$ such that
$t\in \mathbb {R}$ such that  $\theta = \operatorname {Ad}(u)\circ \sigma _t^\varphi$.
$\theta = \operatorname {Ad}(u)\circ \sigma _t^\varphi$.
By the implication (1)![]() $\Rightarrow$(4), we immediately get the following corollary.
$\Rightarrow$(4), we immediately get the following corollary.
Corollary B The Haagerup–Størmer conjecture holds for every type ![]() ${\rm III_1}$ factor with separable predual that has trivial bicentralizer. In particular, the conjecture holds in full generality if Connes’ bicentralizer problem has an affirmative answer.
${\rm III_1}$ factor with separable predual that has trivial bicentralizer. In particular, the conjecture holds in full generality if Connes’ bicentralizer problem has an affirmative answer.
We emphasize that Theorem A applies to all concrete examples of type ![]() ${\rm III_1}$ factors because they have trivial bicentralizers. Although we do not know the complete answer to Connes’ bicentralizer problem, if it is solved affirmatively, then our theorem solves the Haagerup–Størmer conjecture. Even if the problem has a negative answer, we can apply the theorem to every type
${\rm III_1}$ factors because they have trivial bicentralizers. Although we do not know the complete answer to Connes’ bicentralizer problem, if it is solved affirmatively, then our theorem solves the Haagerup–Størmer conjecture. Even if the problem has a negative answer, we can apply the theorem to every type ![]() ${\rm III_1}$ factor up to a tensor product with
${\rm III_1}$ factor up to a tensor product with ![]() $R_\infty$. Thus, in any case, Theorem A covers a large class of type
$R_\infty$. Thus, in any case, Theorem A covers a large class of type ![]() ${\rm III_1}$ factors.
${\rm III_1}$ factors.
We explain item (2) in Theorem A. In all previous works for pointwise inner automorphisms, a specific state (or weight) ![]() $\varphi$ on a factor
$\varphi$ on a factor ![]() $M$ plays a crucial role. More precisely, the implication (1)
$M$ plays a crucial role. More precisely, the implication (1)![]() $\Rightarrow$(2) in Theorem A for the specific
$\Rightarrow$(2) in Theorem A for the specific ![]() $\psi \ (=\varphi )$ is the key step of the proof. For example,
$\psi \ (=\varphi )$ is the key step of the proof. For example, ![]() $\varphi$ is a trace if
$\varphi$ is a trace if ![]() $M$ is of type
$M$ is of type ![]() ${\rm II}$. If
${\rm II}$. If ![]() $M$ is a type
$M$ is a type ![]() ${\rm III}_\lambda$
${\rm III}_\lambda$ ![]() $(0\leq \lambda <1)$ factor, then
$(0\leq \lambda <1)$ factor, then ![]() $\varphi$ is a lacunary weight. We note that, in these cases, the implication (2)
$\varphi$ is a lacunary weight. We note that, in these cases, the implication (2)![]() $\Rightarrow$(4) also follows by the fact that
$\Rightarrow$(4) also follows by the fact that ![]() $\varphi$ is a specific one. Unfortunately, if
$\varphi$ is a specific one. Unfortunately, if ![]() $M$ is a type III
$M$ is a type III![]() $_1$ factor, there are no such specific states or weights in general, and this fact is the main difficulty for the conjecture. We do have a dominant weight, but it is not enough for our purpose because
$_1$ factor, there are no such specific states or weights in general, and this fact is the main difficulty for the conjecture. We do have a dominant weight, but it is not enough for our purpose because ![]() $M_\varphi \subset M$ is not with expectation. In [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24],
$M_\varphi \subset M$ is not with expectation. In [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24], ![]() $\varphi$ is assumed to be an almost periodic state, but not all type
$\varphi$ is assumed to be an almost periodic state, but not all type ![]() ${\rm III_1}$ factors admit such a state.
${\rm III_1}$ factors admit such a state.
In Theorem A, we do not assume ![]() $\varphi$ is such a specific state or weight. We nevertheless prove the implication (1)
$\varphi$ is such a specific state or weight. We nevertheless prove the implication (1)![]() $\Rightarrow$(2). This is the main observation of the paper, so we briefly explain the idea of the proof. Recall that, if
$\Rightarrow$(2). This is the main observation of the paper, so we briefly explain the idea of the proof. Recall that, if ![]() $\varphi$ is almost periodic, each element in
$\varphi$ is almost periodic, each element in ![]() $M$ has a Fourier decomposition along the eigenspaces of
$M$ has a Fourier decomposition along the eigenspaces of ![]() $\varphi$. In [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24], the Fourier decomposition of a unitary element
$\varphi$. In [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24], the Fourier decomposition of a unitary element ![]() $u\in \mathcal {U}(M)$ satisfying
$u\in \mathcal {U}(M)$ satisfying ![]() $\theta (\varphi (a\, \cdot \, )) = u \varphi (a\, \cdot \, )u^*$ for some carefully chosen
$\theta (\varphi (a\, \cdot \, )) = u \varphi (a\, \cdot \, )u^*$ for some carefully chosen ![]() $a\in M_\varphi$ is important in the proof. In our setting, we cannot use such a decomposition since
$a\in M_\varphi$ is important in the proof. In our setting, we cannot use such a decomposition since ![]() $\varphi$ is not assumed to be almost periodic. Instead, we use the embedding
$\varphi$ is not assumed to be almost periodic. Instead, we use the embedding
where the inclusion holds at a continuous core of ![]() $M$. By considering the cases of
$M$. By considering the cases of ![]() $a^p$ for
$a^p$ for ![]() $0< p<1$, we deduce the condition
$0< p<1$, we deduce the condition ![]() $A\preceq _M \theta (A)$ in the sense of Popa's intertwining theory [Reference PopaPop01, Reference PopaPop03]. Then, by the choice of
$A\preceq _M \theta (A)$ in the sense of Popa's intertwining theory [Reference PopaPop01, Reference PopaPop03]. Then, by the choice of ![]() $A$, we get a contradiction and the proof is done. Proving
$A$, we get a contradiction and the proof is done. Proving ![]() $A\preceq _M \theta (A)$ is the key technical step and we do it by the measurable selection principle.
$A\preceq _M \theta (A)$ is the key technical step and we do it by the measurable selection principle.
Once we get (2), since it is a condition for every ![]() $\psi$ with
$\psi$ with ![]() $M_\psi '\cap M=\mathbb {C}$, we can use recent results from Marrakchi's work on relative bicentralizers [Reference MarrakchiMar23] and get (4). Thus, our proof is new even for the Araki–Woods factor
$M_\psi '\cap M=\mathbb {C}$, we can use recent results from Marrakchi's work on relative bicentralizers [Reference MarrakchiMar23] and get (4). Thus, our proof is new even for the Araki–Woods factor ![]() $R_\infty$. This is why we can avoid the use of the classification theorem of
$R_\infty$. This is why we can avoid the use of the classification theorem of ![]() $\operatorname {Aut}(R_\infty )$ [Reference Kawahigashi, Sutherland and TakesakiKST89], which was necessary in all previous works [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24] for the type
$\operatorname {Aut}(R_\infty )$ [Reference Kawahigashi, Sutherland and TakesakiKST89], which was necessary in all previous works [Reference Haagerup and StørmerHS91, Reference Houdayer and IsonoHI24] for the type ![]() ${\rm III_1}$ factor case.
${\rm III_1}$ factor case.
By a result in [Reference Ando, Haagerup, Houdayer and MarrakchiAHHM18], we can also prove the equivalence to item (3) of Theorem A, which is a condition on ultraproducts. This condition is interesting in the sense that ![]() $\varphi ^\omega$ has more information than
$\varphi ^\omega$ has more information than ![]() $\varphi$. Indeed, item (3) is a condition for a single
$\varphi$. Indeed, item (3) is a condition for a single ![]() $\varphi$, while item (2) is one for many
$\varphi$, while item (2) is one for many ![]() $\psi$.
$\psi$.
2. Preliminaries
For a von Neumann algebra ![]() $M$, the
$M$, the ![]() $L^2$-norm with respect to
$L^2$-norm with respect to ![]() $\varphi \in M_\ast ^+$ is denoted by
$\varphi \in M_\ast ^+$ is denoted by ![]() $\| \, \cdot \, \|_{\varphi }$. We use the notation
$\| \, \cdot \, \|_{\varphi }$. We use the notation ![]() $M_p:=pMp$ for each projection
$M_p:=pMp$ for each projection ![]() $p\in M \cup M'$.
$p\in M \cup M'$.
2.1 Tomita–Takesaki theory and Connes cocycles
Let ![]() $M$ be a von Neumann algebra and
$M$ be a von Neumann algebra and ![]() $\varphi \in M_\ast ^+$ a faithful functional. Throughout the paper, the modular action for
$\varphi \in M_\ast ^+$ a faithful functional. Throughout the paper, the modular action for ![]() $\varphi$ is denoted by
$\varphi$ is denoted by ![]() $\sigma ^\varphi \colon \mathbb {R} \curvearrowright M$. The crossed product
$\sigma ^\varphi \colon \mathbb {R} \curvearrowright M$. The crossed product ![]() $M\rtimes _{\sigma ^\varphi }\mathbb {R}$ is called the continuous core (with respect to
$M\rtimes _{\sigma ^\varphi }\mathbb {R}$ is called the continuous core (with respect to ![]() $\varphi$) and is denoted by
$\varphi$) and is denoted by ![]() $C_\varphi (M)$. We say that
$C_\varphi (M)$. We say that ![]() $M$ is a type
$M$ is a type ![]() ${\rm III_1}$ factor if
${\rm III_1}$ factor if ![]() $C_\varphi (M)$ is a factor. The centralizer algebra
$C_\varphi (M)$ is a factor. The centralizer algebra ![]() $M_\varphi$ is the fixed point algebra of the modular action
$M_\varphi$ is the fixed point algebra of the modular action ![]() $\sigma ^\varphi$. See [Reference TakesakiTak03] for details of these objects.
$\sigma ^\varphi$. See [Reference TakesakiTak03] for details of these objects.
Let ![]() $\alpha \colon \mathbb {R} \curvearrowright M$ be a continuous action and
$\alpha \colon \mathbb {R} \curvearrowright M$ be a continuous action and ![]() $p \in M$ a nonzero projection. We say that a
$p \in M$ a nonzero projection. We say that a ![]() $\sigma$-strongly continuous map
$\sigma$-strongly continuous map ![]() $u\colon \mathbb {R} \to pM$ is a generalized cocycle for
$u\colon \mathbb {R} \to pM$ is a generalized cocycle for ![]() $\alpha$ (with support projection
$\alpha$ (with support projection ![]() $p$) if it satisfies
$p$) if it satisfies
In this case, by putting ![]() $\alpha ^u_s(pxp):=u_s\alpha _s(pxp)u_s^*$ for all
$\alpha ^u_s(pxp):=u_s\alpha _s(pxp)u_s^*$ for all ![]() $x\in M$ and
$x\in M$ and ![]() $s\in \mathbb {R}$, we have a continuous
$s\in \mathbb {R}$, we have a continuous ![]() $\mathbb {R}$-action on
$\mathbb {R}$-action on ![]() $pMp$.
$pMp$.
For ![]() $\varphi,\psi \in M_\ast ^+$ with
$\varphi,\psi \in M_\ast ^+$ with ![]() $\varphi$ faithful and with
$\varphi$ faithful and with ![]() $s(\psi )$ the support projection of
$s(\psi )$ the support projection of ![]() $\psi$, consider the modular actions
$\psi$, consider the modular actions ![]() $\sigma ^\varphi$ on
$\sigma ^\varphi$ on ![]() $M$ and
$M$ and ![]() $\sigma ^\psi$ on
$\sigma ^\psi$ on ![]() $M_{s(\psi )}$. The Connes cocycle
$M_{s(\psi )}$. The Connes cocycle ![]() $(u_t)_{t\in \mathbb {R}}$ (for
$(u_t)_{t\in \mathbb {R}}$ (for ![]() $\psi$ with respect to
$\psi$ with respect to ![]() $\varphi$) [Reference ConnesCon72] is a generalized cocycle for
$\varphi$) [Reference ConnesCon72] is a generalized cocycle for ![]() $\sigma ^\varphi$ with support projection
$\sigma ^\varphi$ with support projection ![]() $s(\psi )$ such that
$s(\psi )$ such that ![]() $(\sigma ^\varphi )^{u}\colon \mathbb {R} \curvearrowright M_{s(\psi )}$ coincides with
$(\sigma ^\varphi )^{u}\colon \mathbb {R} \curvearrowright M_{s(\psi )}$ coincides with ![]() $\sigma ^\psi$. We denote it by
$\sigma ^\psi$. We denote it by ![]() $u_t=[D\psi :D\varphi ]_t$ for
$u_t=[D\psi :D\varphi ]_t$ for ![]() $t\in \mathbb {R}$. See [Reference TakesakiTak03, VIII.3.19–20] for this nonfaithful version of the Connes cocycle.
$t\in \mathbb {R}$. See [Reference TakesakiTak03, VIII.3.19–20] for this nonfaithful version of the Connes cocycle.
Let ![]() $\theta = \sigma ^\varphi _t$ for some
$\theta = \sigma ^\varphi _t$ for some ![]() $t\in \mathbb {R}$ and we see that it is pointwise inner. Let
$t\in \mathbb {R}$ and we see that it is pointwise inner. Let ![]() $\psi \in M_\ast ^+$ be a positive functional and take a faithful
$\psi \in M_\ast ^+$ be a positive functional and take a faithful ![]() $\widetilde {\psi }\in M_\ast ^+$ with
$\widetilde {\psi }\in M_\ast ^+$ with ![]() $s(\psi )\widetilde {\psi }=\widetilde {\psi }s(\psi )=\psi$. Then since
$s(\psi )\widetilde {\psi }=\widetilde {\psi }s(\psi )=\psi$. Then since ![]() $s(\psi )\in M_{\widetilde {\psi }}$ and
$s(\psi )\in M_{\widetilde {\psi }}$ and ![]() $\sigma ^{\widetilde {\psi }}_t ( \psi ) = \psi$,
$\sigma ^{\widetilde {\psi }}_t ( \psi ) = \psi$, ![]() $u_t:=[D\varphi :D\widetilde {\psi }]_t$ satisfies
$u_t:=[D\varphi :D\widetilde {\psi }]_t$ satisfies
Hence ![]() $\theta$ is pointwise inner.
$\theta$ is pointwise inner.
By the uniqueness of Connes cocycles, it is straightforward to check that, if ![]() $\varphi,\psi$ are faithful,
$\varphi,\psi$ are faithful, ![]() $v \in M$ a partial isometry with
$v \in M$ a partial isometry with ![]() $e:=v v^*\in M_\psi$,
$e:=v v^*\in M_\psi$, ![]() $v^*v \in M_\varphi$, and
$v^*v \in M_\varphi$, and ![]() $v\varphi v^* = e\psi e$, then for each
$v\varphi v^* = e\psi e$, then for each ![]() $x\in M$ and
$x\in M$ and ![]() $t\in \mathbb {R}$,
$t\in \mathbb {R}$,
We prove some lemmas.
Lemma 2.1 Let ![]() $N\subset M$ be an inclusion of
$N\subset M$ be an inclusion of ![]() $\sigma$-finite von Neumann algebras with expectation
$\sigma$-finite von Neumann algebras with expectation ![]() $E_N$. Let
$E_N$. Let ![]() $\varphi _N\in N_\ast$ be a faithful tracial state and put
$\varphi _N\in N_\ast$ be a faithful tracial state and put ![]() $\varphi :=\varphi _N\circ E_N$. Let
$\varphi :=\varphi _N\circ E_N$. Let ![]() $p,q\in N$ be projections such that
$p,q\in N$ be projections such that ![]() $N_p'\cap M_p\subset N_p$. Assume that there is a
$N_p'\cap M_p\subset N_p$. Assume that there is a ![]() $\ast$-isomorphism
$\ast$-isomorphism ![]() $\theta \colon M_p \to M_q$ such that
$\theta \colon M_p \to M_q$ such that ![]() $\theta (N_p) = N_q$. We write
$\theta (N_p) = N_q$. We write ![]() $\theta _N:=\theta |_{N_p}$.
$\theta _N:=\theta |_{N_p}$.
(1) We have
 $\theta ^{-1}\circ E_N = E_N\circ \theta ^{-1}$ on
$\theta ^{-1}\circ E_N = E_N\circ \theta ^{-1}$ on  $M_q$. In particular,
$M_q$. In particular,
 \[ [Dq\theta(p\varphi p)q:D\varphi]_t = [Dq\theta_N(p\varphi_N p)q :D\varphi_N ]_t \in N,\quad \text{for all }t\in \mathbb{R}. \]
\[ [Dq\theta(p\varphi p)q:D\varphi]_t = [Dq\theta_N(p\varphi_N p)q :D\varphi_N ]_t \in N,\quad \text{for all }t\in \mathbb{R}. \]
(2) There is a unique nonsingular, positive, self-adjoint element
 $h$, which is affiliated with
$h$, which is affiliated with  $N_q$, such that
$N_q$, such that  $q\theta (p\varphi p)q= \varphi _h$.
$q\theta (p\varphi p)q= \varphi _h$.(3) Assume that
 $\theta = \operatorname {Ad}(v)\circ \theta '$ for a
$\theta = \operatorname {Ad}(v)\circ \theta '$ for a  $\ast$-isomorphism
$\ast$-isomorphism  $\theta '\colon pMp\to rMr$, a projection
$\theta '\colon pMp\to rMr$, a projection  $r\in M$, and a partial isometry
$r\in M$, and a partial isometry  $v\in qMr$. Then
$v\in qMr$. Then  $h$ in
$h$ in  $(2)$ satisfies
$(2)$ satisfies
 \[ h^{\mathrm{i} t} = v[D r\theta'(p\varphi p)r : D\varphi]_t \sigma_t^{\varphi}(v^*),\quad \text{for all }t\in \mathbb{R}. \]
\[ h^{\mathrm{i} t} = v[D r\theta'(p\varphi p)r : D\varphi]_t \sigma_t^{\varphi}(v^*),\quad \text{for all }t\in \mathbb{R}. \]
Proof. Recall that a normal conditional expectation from ![]() $M$ onto
$M$ onto ![]() $N$ is unique if
$N$ is unique if ![]() $N\subset M$ is irreducible ([Reference ConnesCon72, § 1.4], [Reference TakesakiTak03, Proposition IX.4.3]). Observe that
$N\subset M$ is irreducible ([Reference ConnesCon72, § 1.4], [Reference TakesakiTak03, Proposition IX.4.3]). Observe that ![]() $N_p\subset M_p$ and
$N_p\subset M_p$ and ![]() $N_q = \theta (N_p)\subset \theta (M_p)=M_q$ are irreducible. In the proof below, for simplicity of notation, we sometimes omit
$N_q = \theta (N_p)\subset \theta (M_p)=M_q$ are irreducible. In the proof below, for simplicity of notation, we sometimes omit ![]() $p$, for example
$p$, for example ![]() $q\theta (\varphi )q = q\theta (p\varphi p)q$.
$q\theta (\varphi )q = q\theta (p\varphi p)q$.
(1) Since ![]() $\theta \circ E_N \circ \theta ^{-1}\colon M_q \to N_q$ is a normal conditional expectation, it coincides with
$\theta \circ E_N \circ \theta ^{-1}\colon M_q \to N_q$ is a normal conditional expectation, it coincides with ![]() $E_N|_{M_q}$ by uniqueness. We get
$E_N|_{M_q}$ by uniqueness. We get ![]() $\theta _N^{-1}\circ E_N = E_N\circ \theta ^{-1}$ on
$\theta _N^{-1}\circ E_N = E_N\circ \theta ^{-1}$ on ![]() $M_q$, and hence
$M_q$, and hence
Take a faithful ![]() $\psi _N\in N_\ast ^+$ with
$\psi _N\in N_\ast ^+$ with ![]() $q \psi _N q = q\theta _N(\varphi _N)q$. Then by [Reference ConnesCon72, Lemma 1.4.4], for each
$q \psi _N q = q\theta _N(\varphi _N)q$. Then by [Reference ConnesCon72, Lemma 1.4.4], for each ![]() $t\in \mathbb {R}$,
$t\in \mathbb {R}$,
(2) Since ![]() $\varphi _{N}$ is a faithful trace on
$\varphi _{N}$ is a faithful trace on ![]() $N$, there is a unique
$N$, there is a unique ![]() $h$, affiliated with
$h$, affiliated with ![]() $N_q$, such that
$N_q$, such that ![]() $q\theta _N(\varphi _N)q = (\varphi _{N})_h$ on
$q\theta _N(\varphi _N)q = (\varphi _{N})_h$ on ![]() $N_q$. Combined with (1), for each
$N_q$. Combined with (1), for each ![]() $t\in \mathbb {R}$, we have
$t\in \mathbb {R}$, we have
Since ![]() $h$ is affiliated with
$h$ is affiliated with ![]() $M_q$, we also have
$M_q$, we also have ![]() $h^{\mathrm {i} t} = [D\varphi _h:D\varphi ]_t$, hence we get
$h^{\mathrm {i} t} = [D\varphi _h:D\varphi ]_t$, hence we get ![]() $q\theta (\varphi )q =\varphi _h$.
$q\theta (\varphi )q =\varphi _h$.
(3) Let ![]() $\psi \in M_\ast ^+$ be a faithful element such that
$\psi \in M_\ast ^+$ be a faithful element such that ![]() $r\in M_\psi$ and
$r\in M_\psi$ and ![]() $r\psi r = r\theta '(\varphi )r$. Then for each
$r\psi r = r\theta '(\varphi )r$. Then for each ![]() $t\in \mathbb {R}$,
$t\in \mathbb {R}$,
 \begin{align*} h^{\mathrm{i} t} &= [Dq\theta(\varphi)q: D\varphi]_t= [D v\theta'(\varphi)v^*: D\varphi]_t\\ &= [D v\psi v^*: D\psi]_t[D \psi: D\varphi]_t\\ &= v\sigma_t^{\psi}(v^*)[D \psi: D\varphi]_t\\ &= v[D \psi: D\varphi]_t \sigma_t^{\varphi}(v^*)= v[D r\psi r : D\varphi]_t \sigma_t^{\varphi}(v^*), \end{align*}
\begin{align*} h^{\mathrm{i} t} &= [Dq\theta(\varphi)q: D\varphi]_t= [D v\theta'(\varphi)v^*: D\varphi]_t\\ &= [D v\psi v^*: D\psi]_t[D \psi: D\varphi]_t\\ &= v\sigma_t^{\psi}(v^*)[D \psi: D\varphi]_t\\ &= v[D \psi: D\varphi]_t \sigma_t^{\varphi}(v^*)= v[D r\psi r : D\varphi]_t \sigma_t^{\varphi}(v^*), \end{align*}
and we are done.
Lemma 2.2 Let ![]() $M$ be a factor with a faithful state
$M$ be a factor with a faithful state ![]() $\varphi \in M_\ast$ such that
$\varphi \in M_\ast$ such that ![]() $M_\varphi ' \cap M =\mathbb {C}$. If
$M_\varphi ' \cap M =\mathbb {C}$. If ![]() $\theta \in \operatorname {Aut}(M)$ satisfies
$\theta \in \operatorname {Aut}(M)$ satisfies ![]() $\theta (M_\varphi )=M_\varphi$, then
$\theta (M_\varphi )=M_\varphi$, then ![]() $\theta (\varphi )=\varphi$. In particular,
$\theta (\varphi )=\varphi$. In particular, ![]() $M_\varphi \subset M$ is singular in the sense that
$M_\varphi \subset M$ is singular in the sense that ![]() $uM_\varphi u^* = M_\varphi$ for
$uM_\varphi u^* = M_\varphi$ for ![]() $u\in \mathcal {U}(M)$ implies
$u\in \mathcal {U}(M)$ implies ![]() $u\in M_\varphi$.
$u\in M_\varphi$.
Proof. Put ![]() $N:=M_\varphi$ and
$N:=M_\varphi$ and ![]() $\varphi _N:=\varphi |_N$. We apply Lemma 2.1(2) for the case
$\varphi _N:=\varphi |_N$. We apply Lemma 2.1(2) for the case ![]() $p=q=1$, and take
$p=q=1$, and take ![]() $h$ such that
$h$ such that ![]() $\theta (\varphi ) = \varphi _h$. Since
$\theta (\varphi ) = \varphi _h$. Since ![]() $h$ is affiliated with
$h$ is affiliated with ![]() $N$, we have
$N$, we have ![]() $\varphi _h|_N =(\varphi _N)_h$. Since
$\varphi _h|_N =(\varphi _N)_h$. Since ![]() $N$ is a finite factor and since
$N$ is a finite factor and since ![]() $\theta (\varphi )|_N$ is a trace, we have
$\theta (\varphi )|_N$ is a trace, we have ![]() $\theta (\varphi )|_N = \varphi _N$ by the uniqueness of the trace. We get
$\theta (\varphi )|_N = \varphi _N$ by the uniqueness of the trace. We get ![]() $(\varphi _N)_h = \varphi _N$ and
$(\varphi _N)_h = \varphi _N$ and ![]() $h=1$. This means
$h=1$. This means ![]() $\theta (\varphi ) = \varphi$.
$\theta (\varphi ) = \varphi$.
If ![]() $uM_\varphi u^* = M_\varphi$ for
$uM_\varphi u^* = M_\varphi$ for ![]() $u\in \mathcal {U}(M)$, we can apply the first part of the lemma to
$u\in \mathcal {U}(M)$, we can apply the first part of the lemma to ![]() $\operatorname {Ad}(u)\in \operatorname {Aut}(M)$. We get
$\operatorname {Ad}(u)\in \operatorname {Aut}(M)$. We get ![]() $\operatorname {Ad}(u)(\varphi )=\varphi$ and hence
$\operatorname {Ad}(u)(\varphi )=\varphi$ and hence ![]() $u$ is contained in
$u$ is contained in ![]() $M_\varphi$.
$M_\varphi$.
Lemma 2.3 Let ![]() $M$ be a factor with a faithful state
$M$ be a factor with a faithful state ![]() $\varphi \in M_\ast$ such that
$\varphi \in M_\ast$ such that ![]() $M_\varphi ' \cap M =\mathbb {C}$. Let
$M_\varphi ' \cap M =\mathbb {C}$. Let ![]() $\theta \in \operatorname {Aut}(M)$ and define an embedding
$\theta \in \operatorname {Aut}(M)$ and define an embedding
If ![]() $\theta (\varphi )=\varphi$, then the following conditions are equivalent:
$\theta (\varphi )=\varphi$, then the following conditions are equivalent:
(1)
 $\theta |_{M_\varphi }$ is outer;
$\theta |_{M_\varphi }$ is outer;(2)
 $\iota _\theta (M_\varphi )'\cap (M\otimes \mathbb {M}_2 ) \subset M\oplus M$.
$\iota _\theta (M_\varphi )'\cap (M\otimes \mathbb {M}_2 ) \subset M\oplus M$.
Proof. If ![]() $\theta |_{M_\varphi } = \operatorname {Ad}(u)$ for some
$\theta |_{M_\varphi } = \operatorname {Ad}(u)$ for some ![]() $u\in \mathcal {U}(M_\varphi )$, then
$u\in \mathcal {U}(M_\varphi )$, then ![]() $\big [{\kern-1.3pt}\begin{smallmatrix} 0 & 0 \\ u & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in
$\big [{\kern-1.3pt}\begin{smallmatrix} 0 & 0 \\ u & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in ![]() $\iota _\theta (M_\varphi )'\cap M\otimes \mathbb {M}_2$.
$\iota _\theta (M_\varphi )'\cap M\otimes \mathbb {M}_2$.
If (2) does not hold, then there is a nonzero ![]() $a\in M$ such that
$a\in M$ such that ![]() $\theta (x)a=ax$ for all
$\theta (x)a=ax$ for all ![]() $x\in M_\varphi$. By
$x\in M_\varphi$. By ![]() $M_\varphi '\cap M=\mathbb {C}$,
$M_\varphi '\cap M=\mathbb {C}$, ![]() $a$ is a scalar multiple of a unitary, so there is a unitary
$a$ is a scalar multiple of a unitary, so there is a unitary ![]() $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that ![]() $\theta (x)=uxu^*$ for all
$\theta (x)=uxu^*$ for all ![]() $x\in M_\varphi$. Then
$x\in M_\varphi$. Then ![]() $\operatorname {Ad}(u)$ globally preserves
$\operatorname {Ad}(u)$ globally preserves ![]() $M_\varphi$, hence
$M_\varphi$, hence ![]() $u$ is in
$u$ is in ![]() $M_\varphi$ by Lemma 2.2. Thus (1) does not hold.
$M_\varphi$ by Lemma 2.2. Thus (1) does not hold.
2.2 Ultraproduct von Neumann algebras
Let ![]() $M$ be a
$M$ be a ![]() $\sigma$-finite von Neumann algebra and
$\sigma$-finite von Neumann algebra and ![]() $\omega$ a free ultrafilter on
$\omega$ a free ultrafilter on ![]() $\mathbb {N}$. Put
$\mathbb {N}$. Put
where ![]() $\ell ^\infty (\mathbb {N}, M)$ is the set of all norm bounded sequences in
$\ell ^\infty (\mathbb {N}, M)$ is the set of all norm bounded sequences in ![]() $M$. The ultraproduct von Neumann algebra [Reference OcneanuOcn85] is defined as the quotient C
$M$. The ultraproduct von Neumann algebra [Reference OcneanuOcn85] is defined as the quotient C![]() $^*$-algebra
$^*$-algebra ![]() $M^\omega := \mathcal {M}^\omega / \mathcal {I}_\omega$, which naturally admits a von Neumann algebra structure. The image of
$M^\omega := \mathcal {M}^\omega / \mathcal {I}_\omega$, which naturally admits a von Neumann algebra structure. The image of ![]() $(x_n)_n$ in
$(x_n)_n$ in ![]() $M^\omega$ is denoted by
$M^\omega$ is denoted by ![]() $(x_n)_\omega$. We have an embedding
$(x_n)_\omega$. We have an embedding ![]() $M \subset M^\omega$ as constant sequences, and this inclusion is with expectation
$M \subset M^\omega$ as constant sequences, and this inclusion is with expectation ![]() $E_\omega$ given by
$E_\omega$ given by ![]() $E_\omega ( (x_n)_\omega )=\sigma \text {-weak}\lim _{n\to \omega }x_n$. For every faithful
$E_\omega ( (x_n)_\omega )=\sigma \text {-weak}\lim _{n\to \omega }x_n$. For every faithful ![]() $\varphi \in M_*^+$, we can define a faithful positive functional
$\varphi \in M_*^+$, we can define a faithful positive functional ![]() $\varphi ^\omega :=\varphi \circ E_\omega$ on
$\varphi ^\omega :=\varphi \circ E_\omega$ on ![]() $M^\omega$.
$M^\omega$.
Every ![]() $\theta \in \operatorname {Aut}(M)$ induces
$\theta \in \operatorname {Aut}(M)$ induces ![]() $\theta ^\omega \in \operatorname {Aut}(M^\omega )$ by the equation
$\theta ^\omega \in \operatorname {Aut}(M^\omega )$ by the equation ![]() $\theta ^\omega ((x_n)_\omega ) = (\theta (x_n))_\omega$. In particular, the modular action of
$\theta ^\omega ((x_n)_\omega ) = (\theta (x_n))_\omega$. In particular, the modular action of ![]() $\varphi ^\omega$ is given by
$\varphi ^\omega$ is given by ![]() $\sigma ^{\varphi ^\omega }_t = (\sigma ^\varphi _t)^\omega$ for all
$\sigma ^{\varphi ^\omega }_t = (\sigma ^\varphi _t)^\omega$ for all ![]() $t\in \mathbb {R}$ [Reference Ando and HaagerupAH12]. For more on ultraproduct von Neumann algebras, we refer the reader to [Reference OcneanuOcn85, Reference Ando and HaagerupAH12].
$t\in \mathbb {R}$ [Reference Ando and HaagerupAH12]. For more on ultraproduct von Neumann algebras, we refer the reader to [Reference OcneanuOcn85, Reference Ando and HaagerupAH12].
2.3 Relative bicentralizer algebras
Let ![]() $N\subset M$ be an inclusion of von Neumann algebras with separable predual and with expectation
$N\subset M$ be an inclusion of von Neumann algebras with separable predual and with expectation ![]() $E_N$. Let
$E_N$. Let ![]() $\varphi \in N_\ast$ be a faithful state and extend it to
$\varphi \in N_\ast$ be a faithful state and extend it to ![]() $M$ by
$M$ by ![]() $E_N$. We define the asymptotic centralizer and the relative bicentralizer algebra (with respect to
$E_N$. We define the asymptotic centralizer and the relative bicentralizer algebra (with respect to ![]() $\varphi$) as
$\varphi$) as
 \begin{align*} \mathrm{AC}_\varphi(N)&:= \{(x_n)_n\in \ell^\infty(\mathbb{N},N) \mid \lim_{n\to \infty}\|x_n\varphi - \varphi x_n\| = 0 \},\\ \mathrm{BC}_\varphi(N\subset M)&:= \{x\in M \mid \lim_{n\to \infty} \|x_n x - x x_n\|_\varphi \to 0 \ \text{for every }(x_n)_n\in \mathrm{AC}_\varphi(N) \}. \end{align*}
\begin{align*} \mathrm{AC}_\varphi(N)&:= \{(x_n)_n\in \ell^\infty(\mathbb{N},N) \mid \lim_{n\to \infty}\|x_n\varphi - \varphi x_n\| = 0 \},\\ \mathrm{BC}_\varphi(N\subset M)&:= \{x\in M \mid \lim_{n\to \infty} \|x_n x - x x_n\|_\varphi \to 0 \ \text{for every }(x_n)_n\in \mathrm{AC}_\varphi(N) \}. \end{align*}
This does not depend on the choice of ![]() $\varphi$ up to a canonical isomorphism, if
$\varphi$ up to a canonical isomorphism, if ![]() $N$ is a type
$N$ is a type ![]() ${\rm III_1}$ factor. In the case
${\rm III_1}$ factor. In the case ![]() $N=M$, we write
$N=M$, we write ![]() $\mathrm {BC}_\varphi (M)=\mathrm {BC}_\varphi (N\subset M)$ and we call it the bicentralizer. Then Connes’ bicentralizer problem asks if every type
$\mathrm {BC}_\varphi (M)=\mathrm {BC}_\varphi (N\subset M)$ and we call it the bicentralizer. Then Connes’ bicentralizer problem asks if every type ![]() ${\rm III_1}$ factor
${\rm III_1}$ factor ![]() $M$ with separable predual has trivial bicentralizer, that is,
$M$ with separable predual has trivial bicentralizer, that is, ![]() $\mathrm {BC_\varphi }(M)=\mathbb {C}$. This condition is equivalent to having a faithful state
$\mathrm {BC_\varphi }(M)=\mathbb {C}$. This condition is equivalent to having a faithful state ![]() $\varphi \in M_\ast$ such that
$\varphi \in M_\ast$ such that ![]() $M_\varphi '\cap M=\mathbb {C}$ [Reference HaagerupHaa85]. Here is a convenient expression by ultraproducts ([Reference Houdayer and IsonoHI15, Proposition 3.3], [Reference Ando, Haagerup, Houdayer and MarrakchiAHHM18, Proposition 3.3]):
$M_\varphi '\cap M=\mathbb {C}$ [Reference HaagerupHaa85]. Here is a convenient expression by ultraproducts ([Reference Houdayer and IsonoHI15, Proposition 3.3], [Reference Ando, Haagerup, Houdayer and MarrakchiAHHM18, Proposition 3.3]):
where ![]() $\omega$ is a fixed free ultrafilter on
$\omega$ is a fixed free ultrafilter on ![]() $\mathbb {N}$.
$\mathbb {N}$.
The next theorem explains the importance of relative bicentralizers. This should be understood as a type III counterpart of Popa's work [Reference PopaPop81].
Theorem 2.4 ([Reference HaagerupHaa85], [Reference Ando, Haagerup, Houdayer and MarrakchiAHHM18, Theorem C])
Assume that ![]() $N$ is a type
$N$ is a type ![]() ${\rm III_1}$ factor. If
${\rm III_1}$ factor. If ![]() $\mathrm {BC}_\varphi (N\subset M) = N'\cap M$, then there exists an amenable subfactor
$\mathrm {BC}_\varphi (N\subset M) = N'\cap M$, then there exists an amenable subfactor ![]() $R \subset N$ of type
$R \subset N$ of type ![]() ${\rm II_1}$ with expectation such that
${\rm II_1}$ with expectation such that ![]() $R'\cap M =N'\cap M$.
$R'\cap M =N'\cap M$.
Very recently, Marrakchi obtained a very general and useful criterion for computations of relative bicentralizers. We will need the following statement. Recall that the inclusion ![]() $N\subset M$ is regular if the normalizer
$N\subset M$ is regular if the normalizer ![]() $\mathcal {N}_M(N):=\{u\in \mathcal {U}(M)\mid uN u^*=N\}$ of
$\mathcal {N}_M(N):=\{u\in \mathcal {U}(M)\mid uN u^*=N\}$ of ![]() $N$ in
$N$ in ![]() $M$ generates
$M$ generates ![]() $M$ as a von Neumann algebra.
$M$ as a von Neumann algebra.
Theorem 2.5 [Reference MarrakchiMar23, Theorem E(5)]
Assume that ![]() $N$ is a type
$N$ is a type ![]() ${\rm III_1}$ factor. Assume that
${\rm III_1}$ factor. Assume that ![]() $N$ has trivial bicentralizer and that
$N$ has trivial bicentralizer and that ![]() $N\subset M$ is regular. If
$N\subset M$ is regular. If ![]() $N'\cap C_\varphi (M)\subset C_\varphi (N)$, then we have
$N'\cap C_\varphi (M)\subset C_\varphi (N)$, then we have ![]() $\mathrm {BC}_\varphi (N\subset M)=\mathbb {C}$.
$\mathrm {BC}_\varphi (N\subset M)=\mathbb {C}$.
Proof. By [Reference MarrakchiMar23, Theorem E(5)], we have
where the relative bicentralizer algebra is defined for arbitrary inclusions. This implies
We get ![]() $\mathrm {BC}_\varphi (N\subset M) \subset \mathrm {BC}_\varphi (N) = \mathbb {C}$.
$\mathrm {BC}_\varphi (N\subset M) \subset \mathrm {BC}_\varphi (N) = \mathbb {C}$.
2.4 Popa's intertwining theory
We recall Popa's intertwining theory [Reference PopaPop01, Reference PopaPop03]. For this, we fix a ![]() $\sigma$-finite von Neumann algebra
$\sigma$-finite von Neumann algebra ![]() $M$ and a finite von Neumann subalgebra
$M$ and a finite von Neumann subalgebra ![]() $B\subset M$ with expectation
$B\subset M$ with expectation ![]() $E_B$. Fix a trace
$E_B$. Fix a trace ![]() $\tau _B$ on
$\tau _B$ on ![]() $B$. We can define a canonical trace
$B$. We can define a canonical trace ![]() $\mathord {\text { Tr}}$ on the basic construction
$\mathord {\text { Tr}}$ on the basic construction ![]() $\langle M, B\rangle$ satisfying
$\langle M, B\rangle$ satisfying ![]() $\mathord {\text { Tr}}( xe_By) = \tau _B\circ E_B(yx)$ for
$\mathord {\text { Tr}}( xe_By) = \tau _B\circ E_B(yx)$ for ![]() $x,y\in M$ (see for example, [Reference Houdayer and IsonoHI15, § 4]).
$x,y\in M$ (see for example, [Reference Houdayer and IsonoHI15, § 4]).
In this setting, we have the following equivalence. For the proof of this theorem, we refer the reader to [Reference Houdayer and IsonoHI15, Theorem 4.3]. Since ![]() $B$ is finite, the canonical operator-valued weight
$B$ is finite, the canonical operator-valued weight ![]() $T_M$ from
$T_M$ from ![]() $\langle M, B\rangle$ to
$\langle M, B\rangle$ to ![]() $M$, which appears in [Reference Houdayer and IsonoHI15, Theorem 4.3 (6)], is unnecessary.
$M$, which appears in [Reference Houdayer and IsonoHI15, Theorem 4.3 (6)], is unnecessary.
Theorem 2.6 [Reference PopaPop01, Reference PopaPop03]
Retain the setting of this section. For a finite von Neumann subalgebra ![]() $A\subset M$ with expectation, the following conditions are equivalent.
$A\subset M$ with expectation, the following conditions are equivalent.
(1) We have
 $A \preceq _M B$. This means that there exist projections
$A \preceq _M B$. This means that there exist projections  $e\in A$,
$e\in A$,  $f\in B$, a partial isometry
$f\in B$, a partial isometry  $v\in eMf$, and a unital normal
$v\in eMf$, and a unital normal  $\ast$-homomorphism
$\ast$-homomorphism  $\theta \colon eAe \to fBf$ such that
$\theta \colon eAe \to fBf$ such that  $v\theta (a)= av$ for all
$v\theta (a)= av$ for all  $a\in eAe$.
$a\in eAe$.(2) There exists no net
 $(u_i)_{i}$ of unitaries in
$(u_i)_{i}$ of unitaries in  $\mathcal {U}(A)$ such that for every
$\mathcal {U}(A)$ such that for every  $a,b\in M$,
$a,b\in M$,
 \[ \|E_B(b^* u_i a )\|_{\tau_B} \rightarrow 0,\quad \text{as}\ i\to \infty. \]
\[ \|E_B(b^* u_i a )\|_{\tau_B} \rightarrow 0,\quad \text{as}\ i\to \infty. \]
(3) There exists a nonzero positive element
 $d\in A' \cap \langle M, B\rangle$ such that
$d\in A' \cap \langle M, B\rangle$ such that  $\mathord {\text { Tr}}(d)<\infty$.
$\mathord {\text { Tr}}(d)<\infty$.
The next three lemmas are well known to experts. We include short proofs for the reader's convenience.
Lemma 2.7 Retain the setting as in Theorem 2.6. Let ![]() $A_1,A_2\subset M$ be finite von Neumann subalgebras with expectation such that
$A_1,A_2\subset M$ be finite von Neumann subalgebras with expectation such that ![]() $A_1$ and
$A_1$ and ![]() $A_2$ are commuting with each other and that
$A_2$ are commuting with each other and that ![]() $A_1\vee A_2\subset M$ is a finite von Neumann subalgebra with expectation.
$A_1\vee A_2\subset M$ is a finite von Neumann subalgebra with expectation.
Suppose that there are nonzero positive elements ![]() $d_i\in A_i' \cap \langle M,B\rangle$ satisfying the condition of item
$d_i\in A_i' \cap \langle M,B\rangle$ satisfying the condition of item ![]() $(3)$ in Theorem 2.6 for
$(3)$ in Theorem 2.6 for ![]() $i=1,2$ such that
$i=1,2$ such that ![]() $d_1d_2\neq 0$. Then we have
$d_1d_2\neq 0$. Then we have ![]() $A_1\vee A_2\preceq _M B$.
$A_1\vee A_2\preceq _M B$.
Proof. Consider ![]() $\mathord {\text { Tr}}$ on
$\mathord {\text { Tr}}$ on ![]() $\langle M,B\rangle$ as in Theorem 2.6. Put
$\langle M,B\rangle$ as in Theorem 2.6. Put
By the normality of ![]() $\mathord {\text { Tr}}$, every element in
$\mathord {\text { Tr}}$, every element in ![]() $\mathcal {K}$ has finite value in
$\mathcal {K}$ has finite value in ![]() $\mathord {\text { Tr}}$. By regarding
$\mathord {\text { Tr}}$. By regarding ![]() $\mathcal {K}$ as a closed subset of
$\mathcal {K}$ as a closed subset of ![]() $L^2(\langle M,B\rangle,\mathord {\text { Tr}})$ (see [Reference Houdayer and IsonoHI15, Lemma 4.4]), take the unique element
$L^2(\langle M,B\rangle,\mathord {\text { Tr}})$ (see [Reference Houdayer and IsonoHI15, Lemma 4.4]), take the unique element ![]() $d\in \mathcal {K}$ which has the minimum distance from
$d\in \mathcal {K}$ which has the minimum distance from ![]() $0$. The uniqueness condition implies
$0$. The uniqueness condition implies ![]() $udu^*=u$ for all
$udu^*=u$ for all ![]() $u\in \mathcal {U}(A_2)$, hence
$u\in \mathcal {U}(A_2)$, hence ![]() $d$ is contained in
$d$ is contained in ![]() $(A_1\vee A_2)'\cap \langle M,B\rangle$. Then observe that
$(A_1\vee A_2)'\cap \langle M,B\rangle$. Then observe that ![]() $d_1,d_2\in L^2(\langle M,B\rangle,\mathord {\text { Tr}})$, and for each
$d_1,d_2\in L^2(\langle M,B\rangle,\mathord {\text { Tr}})$, and for each ![]() $u\in \mathcal {U}(A_2)$,
$u\in \mathcal {U}(A_2)$,
This implies that ![]() $\mathcal {K}$ does not contain
$\mathcal {K}$ does not contain ![]() $0$, hence
$0$, hence ![]() $d\neq 0$. This implies
$d\neq 0$. This implies ![]() $A_1\vee A_2\preceq _M B$.
$A_1\vee A_2\preceq _M B$.
Lemma 2.8 Let ![]() $M$ be a von Neumann algebra,
$M$ be a von Neumann algebra, ![]() $\varphi \in M_\ast$ a faithful state, and
$\varphi \in M_\ast$ a faithful state, and ![]() $A,B\subset M_\varphi$ von Neumann subalgebras. If
$A,B\subset M_\varphi$ von Neumann subalgebras. If ![]() $A\not \preceq _M B$, then
$A\not \preceq _M B$, then ![]() $A\mathbin {\overline {\otimes }} L\mathbb {R} \not \preceq _{C_\varphi (M)} B\mathbin {\overline {\otimes }} L\mathbb {R}$.
$A\mathbin {\overline {\otimes }} L\mathbb {R} \not \preceq _{C_\varphi (M)} B\mathbin {\overline {\otimes }} L\mathbb {R}$.
Proof. Let ![]() $E_B\colon M\to B$ be the unique
$E_B\colon M\to B$ be the unique ![]() $\varphi$-preserving conditional expectation. Then since
$\varphi$-preserving conditional expectation. Then since ![]() $E_B$ commutes with
$E_B$ commutes with ![]() $\sigma ^\varphi$, we can extend
$\sigma ^\varphi$, we can extend ![]() $E_B$ to one from
$E_B$ to one from ![]() $C_\varphi (M)$ onto
$C_\varphi (M)$ onto ![]() $B\mathbin {\overline {\otimes }} L\mathbb {R}$. Take a net
$B\mathbin {\overline {\otimes }} L\mathbb {R}$. Take a net ![]() $(u_i)_i$ of
$(u_i)_i$ of ![]() $\mathcal {U}(A)$ as in item (2) in Theorem 2.6. Then it is easy to see that
$\mathcal {U}(A)$ as in item (2) in Theorem 2.6. Then it is easy to see that ![]() $(u_i\otimes 1_{L\mathbb {R}})_i$ works for
$(u_i\otimes 1_{L\mathbb {R}})_i$ works for ![]() $A\mathbin {\overline {\otimes }} L\mathbb {R}\not \preceq _{C_\varphi (M)} B\mathbin {\overline {\otimes }} L\mathbb {R}$.
$A\mathbin {\overline {\otimes }} L\mathbb {R}\not \preceq _{C_\varphi (M)} B\mathbin {\overline {\otimes }} L\mathbb {R}$.
In the lemma below, we need the case that ![]() $A,B \subset M$ are possibly nonunital finite von Neumann subalgebras, where subalgebras
$A,B \subset M$ are possibly nonunital finite von Neumann subalgebras, where subalgebras ![]() $A\subset 1_A M 1_A$ and
$A\subset 1_A M 1_A$ and ![]() $B\subset 1_B M1_B$ with units
$B\subset 1_B M1_B$ with units ![]() $1_A,1_B$ are assumed to be with expectation. In this case, we can use the same definition for
$1_A,1_B$ are assumed to be with expectation. In this case, we can use the same definition for ![]() $A\preceq _M B$, and item (2) in Theorem 2.6 works by replacing
$A\preceq _M B$, and item (2) in Theorem 2.6 works by replacing ![]() $a,b\in M$ by
$a,b\in M$ by ![]() $a,b\in M1_B$. Item (3) is slightly more complicated, but we do not need it. See [Reference Houdayer and IsonoHI15, Theorem 4.3] for more on the nonunital case.
$a,b\in M1_B$. Item (3) is slightly more complicated, but we do not need it. See [Reference Houdayer and IsonoHI15, Theorem 4.3] for more on the nonunital case.
Lemma 2.9 Let ![]() $A,B_1,\ldots,B_n\subset M$ be (possibly nonunital) inclusions of
$A,B_1,\ldots,B_n\subset M$ be (possibly nonunital) inclusions of ![]() $\sigma$-finite von Neumann algebras with expectation. Let
$\sigma$-finite von Neumann algebras with expectation. Let ![]() $E_{B_k}\colon M_{1_{B_k}}\to B_k$ be faithful normal conditional expectations for all
$E_{B_k}\colon M_{1_{B_k}}\to B_k$ be faithful normal conditional expectations for all ![]() $k$ and assume that
$k$ and assume that ![]() $A,B_1,\ldots,B_n$ are finite with trace
$A,B_1,\ldots,B_n$ are finite with trace ![]() $\tau _k\in (B_k)_\ast$ for all
$\tau _k\in (B_k)_\ast$ for all ![]() $k$. If
$k$. If ![]() $A\not \preceq _M B_k$ for all
$A\not \preceq _M B_k$ for all ![]() $k$, then there exists a net
$k$, then there exists a net ![]() $(u_i)_{i}$ in
$(u_i)_{i}$ in ![]() $\mathcal {U}(A)$ such that for all
$\mathcal {U}(A)$ such that for all ![]() $k$,
$k$,
Proof. Consider ![]() $M_n:=M\otimes \mathbb {C}^n$ and embeddings
$M_n:=M\otimes \mathbb {C}^n$ and embeddings
Observe that ![]() $A\not \preceq _M B_k$ implies
$A\not \preceq _M B_k$ implies ![]() $\widetilde {A}\not \preceq _{M_n} B_k$ for all
$\widetilde {A}\not \preceq _{M_n} B_k$ for all ![]() $k$ (use item (2) of Theorem 2.6). Then by [Reference Houdayer and IsonoHI15, Remark 4.2(2)], we have that
$k$ (use item (2) of Theorem 2.6). Then by [Reference Houdayer and IsonoHI15, Remark 4.2(2)], we have that ![]() $\widetilde {A}\not \preceq _{M_n} \widetilde {B}$. Then a net of unitaries in item
$\widetilde {A}\not \preceq _{M_n} \widetilde {B}$. Then a net of unitaries in item ![]() $(2)$ of Theorem 2.6 for
$(2)$ of Theorem 2.6 for ![]() $\widetilde {A}\not \preceq _{M_n} \widetilde {B}$ works.
$\widetilde {A}\not \preceq _{M_n} \widetilde {B}$ works.
3. Proof of Theorem A: (1) $\Rightarrow$(2)
$\Rightarrow$(2)
We need two lemmas. The first one uses the measurable selection principle.
Lemma 3.1 Let ![]() $M$ be a von Neumann algebra with separable predual,
$M$ be a von Neumann algebra with separable predual, ![]() $\varphi$ a faithful normal state, and
$\varphi$ a faithful normal state, and ![]() $\theta \in \operatorname {Aut}(M)$ a pointwise inner automorphism. Then for each positive element
$\theta \in \operatorname {Aut}(M)$ a pointwise inner automorphism. Then for each positive element ![]() $a\in M_\varphi$, there exist a compact subset
$a\in M_\varphi$, there exist a compact subset ![]() $K\subset (0,1)$ with positive Lebesgue measure, and a continuous map
$K\subset (0,1)$ with positive Lebesgue measure, and a continuous map ![]() $K \ni p\mapsto u_p\in \mathcal {U}(M)$ such that
$K \ni p\mapsto u_p\in \mathcal {U}(M)$ such that
where ![]() $\mathcal {U}(M)$ is equipped with the
$\mathcal {U}(M)$ is equipped with the ![]() $\ast$-strong topology.
$\ast$-strong topology.
Proof. Throughout the proof, we consider the ![]() $\ast$-strong topology for
$\ast$-strong topology for ![]() $\mathcal {U}(M)$ and we regard it as a Polish space. Set
$\mathcal {U}(M)$ and we regard it as a Polish space. Set
Then it is easy to see that ![]() $\mathcal {S}$ is a closed subset. Since
$\mathcal {S}$ is a closed subset. Since ![]() $\theta$ is pointwise inner, we have
$\theta$ is pointwise inner, we have ![]() $(0,1)=\pi _1(\mathcal {S})$, where
$(0,1)=\pi _1(\mathcal {S})$, where ![]() $\pi _1$ is the projection onto the first coordinate. Hence, with the Lebesgue measure on
$\pi _1$ is the projection onto the first coordinate. Hence, with the Lebesgue measure on ![]() $(0,1)$, we can apply the measurable selection principle (e.g. [Reference Kadison and RingroseKR97, Theorem 14.3.6]) and find a Lebesgue measurable map
$(0,1)$, we can apply the measurable selection principle (e.g. [Reference Kadison and RingroseKR97, Theorem 14.3.6]) and find a Lebesgue measurable map
such that ![]() $(p,\eta (p)) \in \mathcal {S}$ for all
$(p,\eta (p)) \in \mathcal {S}$ for all ![]() $p\in (0,1)$. Since
$p\in (0,1)$. Since ![]() $\mathcal {U}(M)$ is a Polish space, we can apply Lusin's theorem to
$\mathcal {U}(M)$ is a Polish space, we can apply Lusin's theorem to ![]() $\eta$ and find a compact subset
$\eta$ and find a compact subset ![]() $K\subset (0,1)$ such that
$K\subset (0,1)$ such that ![]() $\eta |_{K}$ is continuous and that
$\eta |_{K}$ is continuous and that ![]() $(0,1)\setminus K$ has arbitrarily small Lebesgue measure. The conclusion follows.
$(0,1)\setminus K$ has arbitrarily small Lebesgue measure. The conclusion follows.
The second lemma uses the first. This lemma is the key observation of the paper.
Lemma 3.2 Let ![]() $M$ be a von Neumann algebra with separable predual,
$M$ be a von Neumann algebra with separable predual, ![]() $\varphi \in M_\ast$ a faithful state, and
$\varphi \in M_\ast$ a faithful state, and ![]() $\theta \in \operatorname {Aut}(M)$ a pointwise inner automorphism such that
$\theta \in \operatorname {Aut}(M)$ a pointwise inner automorphism such that ![]() $\theta (\varphi )=\varphi$. Then, for each positive invertible element
$\theta (\varphi )=\varphi$. Then, for each positive invertible element ![]() $a\in M_\varphi$, we have
$a\in M_\varphi$, we have ![]() $A\preceq _M \theta (A)$, where
$A\preceq _M \theta (A)$, where ![]() $A:=\mathrm {W}^*\{a\}\subset M_\varphi$.
$A:=\mathrm {W}^*\{a\}\subset M_\varphi$.
Proof. Observe that ![]() $\theta (M_\varphi )=M_\varphi$ and
$\theta (M_\varphi )=M_\varphi$ and ![]() $\theta (A)\subset M_\varphi$. Take
$\theta (A)\subset M_\varphi$. Take ![]() $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that ![]() $\varphi _{\theta (a)} = \theta (\varphi _a) = u \varphi _a u^*$. Then since
$\varphi _{\theta (a)} = \theta (\varphi _a) = u \varphi _a u^*$. Then since
and
we get ![]() $\theta (a^{\mathrm {i} t}) = u a^{\mathrm {i} t} \sigma _t^{\varphi } (u^*)$ for all
$\theta (a^{\mathrm {i} t}) = u a^{\mathrm {i} t} \sigma _t^{\varphi } (u^*)$ for all ![]() $t\in \mathbb {R}$. Define
$t\in \mathbb {R}$. Define
where ![]() $\lambda _t$ denotes the left regular representation on
$\lambda _t$ denotes the left regular representation on ![]() $L^2(\mathbb {R})$, and observe that
$L^2(\mathbb {R})$, and observe that ![]() $\widetilde {A}\subset C_\varphi (M)$ is with expectation. Then it is easy to see that
$\widetilde {A}\subset C_\varphi (M)$ is with expectation. Then it is easy to see that ![]() $\operatorname {Ad}(u)$ restricts to a
$\operatorname {Ad}(u)$ restricts to a ![]() $\ast$-homomorphism from
$\ast$-homomorphism from ![]() $\widetilde {A}$ into
$\widetilde {A}$ into ![]() $\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$, so that we get
$\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$, so that we get ![]() $\widetilde {A}\preceq _{C_\varphi (M)} \theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$. More precisely, if we denote by
$\widetilde {A}\preceq _{C_\varphi (M)} \theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$. More precisely, if we denote by ![]() $e$ the Jones projection for a fixed faithful normal conditional expectation from
$e$ the Jones projection for a fixed faithful normal conditional expectation from ![]() $C_\varphi (M)$ onto
$C_\varphi (M)$ onto ![]() $\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$, then the projection
$\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$, then the projection ![]() $u^* e u$ satisfies the condition of item
$u^* e u$ satisfies the condition of item ![]() $(3)$ in Theorem 2.6.
$(3)$ in Theorem 2.6.
Fix ![]() $0< p<1$, and we consider the positive invertible element
$0< p<1$, and we consider the positive invertible element ![]() $a^p$. Then, by the same reasoning as above, we have that
$a^p$. Then, by the same reasoning as above, we have that
together with the projection ![]() $u_p^* e u_p$, where
$u_p^* e u_p$, where ![]() $u_p$ is a unitary satisfying
$u_p$ is a unitary satisfying ![]() $\varphi _{\theta (a^p)} = u_p \varphi _{a^p} u_p^*$. We note that the algebra
$\varphi _{\theta (a^p)} = u_p \varphi _{a^p} u_p^*$. We note that the algebra ![]() $\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$ does not depend on
$\theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$ does not depend on ![]() $p$.
$p$.
Now we claim that ![]() $A\mathbin {\overline {\otimes }} L\mathbb {R} \preceq _{C_\varphi (M)} \theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$. To see this, we first apply Lemma 3.1 and find a compact
$A\mathbin {\overline {\otimes }} L\mathbb {R} \preceq _{C_\varphi (M)} \theta (A)\mathbin {\overline {\otimes }} L\mathbb {R}$. To see this, we first apply Lemma 3.1 and find a compact ![]() $K\subset (0,1)$ with positive measure and a continuous map
$K\subset (0,1)$ with positive measure and a continuous map ![]() $K\ni p \mapsto u_p$. Then we take a sequence
$K\ni p \mapsto u_p$. Then we take a sequence ![]() $p_n\in K$ such that
$p_n\in K$ such that ![]() $p_n$ converges to
$p_n$ converges to ![]() $p\in K$ and
$p\in K$ and ![]() $p\not \in \{p_n\}_n$. Then
$p\not \in \{p_n\}_n$. Then ![]() $u_{p_n} \to u_p$ in the
$u_{p_n} \to u_p$ in the ![]() $\ast$-strong topology, hence
$\ast$-strong topology, hence
as well. In particular, we can find ![]() $p_n=:q$ such that
$p_n=:q$ such that ![]() $q\neq p$ and
$q\neq p$ and ![]() $d_q d_p\neq 0$. Observe that
$d_q d_p\neq 0$. Observe that ![]() $\widetilde { A}_p\vee \widetilde {A}_q=A\mathbin {\overline {\otimes }} L\mathbb {R}$, which is a finite von Neumann subalgebra in
$\widetilde { A}_p\vee \widetilde {A}_q=A\mathbin {\overline {\otimes }} L\mathbb {R}$, which is a finite von Neumann subalgebra in ![]() $C_\varphi (M)$ with expectation. Then by Lemma 2.7, we have that
$C_\varphi (M)$ with expectation. Then by Lemma 2.7, we have that
Hence the claim is proven.
Finally, this condition implies ![]() $A\preceq _M \theta (A)$ by Lemma 2.8.
$A\preceq _M \theta (A)$ by Lemma 2.8.
Now we prove (1)![]() $\Rightarrow$(2) of Theorem A. For the proof, we need Popa's
$\Rightarrow$(2) of Theorem A. For the proof, we need Popa's ![]() $\mathcal {G}$-singular maximal abelian
$\mathcal {G}$-singular maximal abelian ![]() $\ast$-subalgebra (MASA) technique for type
$\ast$-subalgebra (MASA) technique for type ![]() ${\rm III_1}$ factors; see Theorem A.1.
${\rm III_1}$ factors; see Theorem A.1.
Proof of Theorem A: (1)other$\Rightarrow$(2) Let ![]() $\psi \in M_\ast ^+$ be a faithful state such that
$\psi \in M_\ast ^+$ be a faithful state such that ![]() $M_\psi '\cap M=\mathbb {C}$. Since
$M_\psi '\cap M=\mathbb {C}$. Since ![]() $\theta$ is pointwise inner, there is
$\theta$ is pointwise inner, there is ![]() $v\in \mathcal {U}(M)$ such that
$v\in \mathcal {U}(M)$ such that ![]() $\operatorname {Ad}(v)\circ \theta (\psi )=\psi$. So up to replacing
$\operatorname {Ad}(v)\circ \theta (\psi )=\psi$. So up to replacing ![]() $\operatorname {Ad}(v)\circ \theta$ by
$\operatorname {Ad}(v)\circ \theta$ by ![]() $\theta$, we may assume
$\theta$, we may assume ![]() $\theta (\psi )=\psi$. Then we show that
$\theta (\psi )=\psi$. Then we show that ![]() $\theta |_{M_\psi }$ is inner.
$\theta |_{M_\psi }$ is inner.
Suppose by contradiction that ![]() $\theta$ is not inner on
$\theta$ is not inner on ![]() $M_\psi$. Then, putting
$M_\psi$. Then, putting ![]() $\mathcal {G}:=\{{\text { id}}_M,\ \theta ^{-1}\}$, we apply Theorem A.1 and take a
$\mathcal {G}:=\{{\text { id}}_M,\ \theta ^{-1}\}$, we apply Theorem A.1 and take a ![]() $\mathcal {G}$-singular MASA
$\mathcal {G}$-singular MASA ![]() $A\subset M_\psi$. Take a generator
$A\subset M_\psi$. Take a generator ![]() $a$ of
$a$ of ![]() $A$ which is positive and invertible. We can apply Lemma 3.2 to
$A$ which is positive and invertible. We can apply Lemma 3.2 to ![]() $a$ and get
$a$ and get ![]() $A\preceq _M \theta (A)$. Since
$A\preceq _M \theta (A)$. Since ![]() $A$ and
$A$ and ![]() $\theta (A)$ are MASAs in
$\theta (A)$ are MASAs in ![]() $M$, by [Reference Houdayer and VaesHV12, Theorem 2.5], one can find a nonzero partial isometry
$M$, by [Reference Houdayer and VaesHV12, Theorem 2.5], one can find a nonzero partial isometry ![]() $v\in M$ such that
$v\in M$ such that
Thus ![]() $\operatorname {Ad}(v)$ restricts to a
$\operatorname {Ad}(v)$ restricts to a ![]() $\ast$-isomorphism from
$\ast$-isomorphism from ![]() $Av^*v$ onto
$Av^*v$ onto ![]() $\theta (A)vv^*$. Since
$\theta (A)vv^*$. Since ![]() $A$ is diffuse, up to exchanging
$A$ is diffuse, up to exchanging ![]() $v^*v$ with a smaller projection in
$v^*v$ with a smaller projection in ![]() $A$ (or
$A$ (or ![]() $vv^*$ with one in
$vv^*$ with one in ![]() $\theta (A)$) if necessary, we may assume
$\theta (A)$) if necessary, we may assume ![]() $v^*v\neq 1$ and
$v^*v\neq 1$ and ![]() $vv^*\neq 1$. Then since
$vv^*\neq 1$. Then since ![]() $M$ is a type III factor,
$M$ is a type III factor, ![]() $1-v^*v$ and
$1-v^*v$ and ![]() $1-vv^*$ are equivalent, so we can take a partial isometry
$1-vv^*$ are equivalent, so we can take a partial isometry ![]() $w\in M$ such that
$w\in M$ such that ![]() $w^*w=1-v^*v$ and
$w^*w=1-v^*v$ and ![]() $ww^* = 1-vv^*$. Then
$ww^* = 1-vv^*$. Then ![]() $\widetilde {v}:= v+w\in M$ is a unitary element satisfying
$\widetilde {v}:= v+w\in M$ is a unitary element satisfying ![]() $\widetilde {v}p = v$ where
$\widetilde {v}p = v$ where ![]() $p:=v^*v$, so that
$p:=v^*v$, so that
This means ![]() $\operatorname {Ad}(\theta ^{-1}(\widetilde {v})) \circ \theta ^{-1} (A p) \subset A.$ By
$\operatorname {Ad}(\theta ^{-1}(\widetilde {v})) \circ \theta ^{-1} (A p) \subset A.$ By ![]() $\mathcal {G}$-singularity, we have that
$\mathcal {G}$-singularity, we have that ![]() $\theta ^{-1}={\text { id}}_M$, a contradiction.
$\theta ^{-1}={\text { id}}_M$, a contradiction.
4. Proof of Theorem A: (2) $\Rightarrow$(3) and (3)
$\Rightarrow$(3) and (3) $\Rightarrow$(4)
$\Rightarrow$(4)
Proof of Theorem A: (2)![]() $\Rightarrow$(3) We may assume that
$\Rightarrow$(3) We may assume that ![]() $\theta$ is outer on
$\theta$ is outer on ![]() $M$. Set
$M$. Set ![]() $M_2:=M\otimes \mathbb {M}_2$ and consider an embedding
$M_2:=M\otimes \mathbb {M}_2$ and consider an embedding ![]() $\iota _\theta \colon M\to M_2$ with expectation as in Lemma 2.3. Since
$\iota _\theta \colon M\to M_2$ with expectation as in Lemma 2.3. Since ![]() $\theta$ is outer, we have
$\theta$ is outer, we have ![]() $M'\cap M_2 = \mathbb {C} \oplus \mathbb {C}$. We consider the relative bicentralizer
$M'\cap M_2 = \mathbb {C} \oplus \mathbb {C}$. We consider the relative bicentralizer
We claim ![]() $\mathrm {BC}_\varphi (M\subset M_2)\neq M'\cap M_2$.
$\mathrm {BC}_\varphi (M\subset M_2)\neq M'\cap M_2$.
To see this, suppose by contradiction that ![]() $\mathrm {BC}_\varphi (M\subset M_2)=M'\cap M_2$. Then by Theorem 2.4, there is an amenable
$\mathrm {BC}_\varphi (M\subset M_2)=M'\cap M_2$. Then by Theorem 2.4, there is an amenable ![]() ${\rm II_1}$ factor
${\rm II_1}$ factor ![]() $R\subset M$ with expectation
$R\subset M$ with expectation ![]() $E_R$ such that
$E_R$ such that ![]() $R'\cap M_2 = M'\cap M_2 = \mathbb {C}\oplus \mathbb {C}$. Put
$R'\cap M_2 = M'\cap M_2 = \mathbb {C}\oplus \mathbb {C}$. Put ![]() $\psi :=\tau _R\circ E_R$, where
$\psi :=\tau _R\circ E_R$, where ![]() $\tau _R$ is the trace on
$\tau _R$ is the trace on ![]() $R$, and observe that
$R$, and observe that ![]() $R\subset M_\psi \subset M$. Then since
$R\subset M_\psi \subset M$. Then since ![]() $M_\psi '\cap M\subset R'\cap M=\mathbb {C}$ (this follows by
$M_\psi '\cap M\subset R'\cap M=\mathbb {C}$ (this follows by ![]() $R'\cap M_2=\mathbb {C}\oplus \mathbb {C}$), by assumption, there is
$R'\cap M_2=\mathbb {C}\oplus \mathbb {C}$), by assumption, there is ![]() $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that ![]() $\operatorname {Ad}(u)\circ \theta |_{M_\psi } = {\text { id}}_{M_\psi }$. Then
$\operatorname {Ad}(u)\circ \theta |_{M_\psi } = {\text { id}}_{M_\psi }$. Then ![]() $\big[{\kern-1.3pt}\begin{smallmatrix} 0 & u \\ 0 & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in
$\big[{\kern-1.3pt}\begin{smallmatrix} 0 & u \\ 0 & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in ![]() $M_\psi '\cap M_2 \subset R'\cap M_2 = \mathbb {C}\oplus \mathbb {C}$. This is a contradiction and the claim is proven.
$M_\psi '\cap M_2 \subset R'\cap M_2 = \mathbb {C}\oplus \mathbb {C}$. This is a contradiction and the claim is proven.
We take ![]() $\big [{\kern-1.3pt}\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}{\kern-1.3pt}\big ]\in (M^\omega )_{\varphi ^\omega }' \cap M_2$, which is not contained in
$\big [{\kern-1.3pt}\begin{smallmatrix} a & b \\ c & d \end{smallmatrix}{\kern-1.3pt}\big ]\in (M^\omega )_{\varphi ^\omega }' \cap M_2$, which is not contained in ![]() $\mathbb {C}\oplus \mathbb {C}$. Then since
$\mathbb {C}\oplus \mathbb {C}$. Then since ![]() $(M^\omega )_{\varphi ^\omega }' \cap M = \mathrm {BC}_\varphi (M)=\mathbb {C}$, we have
$(M^\omega )_{\varphi ^\omega }' \cap M = \mathrm {BC}_\varphi (M)=\mathbb {C}$, we have ![]() $a,d\in \mathbb {C}$, hence
$a,d\in \mathbb {C}$, hence ![]() $b\neq 0$ or
$b\neq 0$ or ![]() $c\neq 0$. By taking the adjoint if necessary, we may assume
$c\neq 0$. By taking the adjoint if necessary, we may assume ![]() $c\neq 0$. Then observe that
$c\neq 0$. Then observe that ![]() $\theta ^\omega (x)c = cx$ for all
$\theta ^\omega (x)c = cx$ for all ![]() $x\in (M^\omega )_{\varphi ^\omega }$. Since
$x\in (M^\omega )_{\varphi ^\omega }$. Since ![]() $(M^\omega )_{\varphi ^\omega }' \cap M =\mathbb {C}$, by the polar decomposition, we can replace
$(M^\omega )_{\varphi ^\omega }' \cap M =\mathbb {C}$, by the polar decomposition, we can replace ![]() $c$ by a unitary element. This means (3) holds.
$c$ by a unitary element. This means (3) holds.
Proof Theorem A: (3)other$\Rightarrow$(4) By assumption, take ![]() $u\in \mathcal {U}(M)$ such that
$u\in \mathcal {U}(M)$ such that ![]() $\operatorname {Ad}(u)\circ \theta ^\omega = {\text { id}}$ on
$\operatorname {Ad}(u)\circ \theta ^\omega = {\text { id}}$ on ![]() $(M^\omega )_{\varphi ^\omega }$. Up to replacing
$(M^\omega )_{\varphi ^\omega }$. Up to replacing ![]() $\operatorname {Ad}(u)\circ \theta$ by
$\operatorname {Ad}(u)\circ \theta$ by ![]() $\theta$, we may assume
$\theta$, we may assume ![]() $u=1$. Then by Lemma 2.2, we have that
$u=1$. Then by Lemma 2.2, we have that ![]() $\theta (\varphi )=\varphi$. In particular,
$\theta (\varphi )=\varphi$. In particular, ![]() $\theta$ commutes with the modular action of
$\theta$ commutes with the modular action of ![]() $\varphi$.
$\varphi$.
We set
Observe that by ![]() $M_\varphi '\cap M=\mathbb {C}$ and
$M_\varphi '\cap M=\mathbb {C}$ and ![]() $\theta |_{M_\varphi }={\text { id}}$, the equality
$\theta |_{M_\varphi }={\text { id}}$, the equality ![]() $\theta ^n = \operatorname {Ad}(u)\circ \sigma ^\varphi _t$ implies
$\theta ^n = \operatorname {Ad}(u)\circ \sigma ^\varphi _t$ implies ![]() $u\in \mathbb {C}$, so we can actually remove
$u\in \mathbb {C}$, so we can actually remove ![]() $u\in \mathcal {U}(M)$ in the definition of
$u\in \mathcal {U}(M)$ in the definition of ![]() $H(\theta )$. Since
$H(\theta )$. Since ![]() $H(\theta )$ is a subgroup in
$H(\theta )$ is a subgroup in ![]() $\mathbb {Z}$, we can write
$\mathbb {Z}$, we can write ![]() $H(\theta )= k\mathbb {Z}$ for some
$H(\theta )= k\mathbb {Z}$ for some ![]() $k\geq 0$.
$k\geq 0$.
Assume that ![]() $k>0$ and
$k>0$ and ![]() $\theta ^k= \sigma ^\varphi _t$. Then, putting
$\theta ^k= \sigma ^\varphi _t$. Then, putting ![]() $\widetilde {\theta }:=\sigma ^\varphi _{-t/k}\circ \theta$, observe that
$\widetilde {\theta }:=\sigma ^\varphi _{-t/k}\circ \theta$, observe that ![]() $H(\widetilde {\theta })=H(\theta )$,
$H(\widetilde {\theta })=H(\theta )$, ![]() $\widetilde {\theta }^k={\text { id}}$, and
$\widetilde {\theta }^k={\text { id}}$, and ![]() $\widetilde {\theta }^\omega ={\text { id}}$ on
$\widetilde {\theta }^\omega ={\text { id}}$ on ![]() $(M^\omega )_{\varphi ^\omega }$. Hence up to replacing
$(M^\omega )_{\varphi ^\omega }$. Hence up to replacing ![]() $\widetilde {\theta }$ by
$\widetilde {\theta }$ by ![]() $\theta$, we may assume
$\theta$, we may assume ![]() $\theta ^k ={\text { id}}$. If
$\theta ^k ={\text { id}}$. If ![]() $k=0$, we do not need this replacement.
$k=0$, we do not need this replacement.
For each ![]() $k\geq 0$, set
$k\geq 0$, set ![]() $G:=\mathbb {Z}/k\mathbb {Z}$ and define an outer action
$G:=\mathbb {Z}/k\mathbb {Z}$ and define an outer action ![]() $G\curvearrowright M$ given by
$G\curvearrowright M$ given by ![]() $\{\theta ^n\}_{n\in \mathbb {Z}}$. We denote this action again by
$\{\theta ^n\}_{n\in \mathbb {Z}}$. We denote this action again by ![]() $\theta$. Put
$\theta$. Put ![]() $\widetilde {M}:=M\rtimes _\theta G$ with canonical expectation
$\widetilde {M}:=M\rtimes _\theta G$ with canonical expectation ![]() $E_M\colon \widetilde {M}\to M$ and note that
$E_M\colon \widetilde {M}\to M$ and note that ![]() $M'\cap \widetilde {M}=\mathbb {C}$ by the outerness of
$M'\cap \widetilde {M}=\mathbb {C}$ by the outerness of ![]() $\theta$. We extend
$\theta$. We extend ![]() $\varphi$ to
$\varphi$ to ![]() $\widetilde {M}$ by
$\widetilde {M}$ by ![]() $E_M$. Since
$E_M$. Since ![]() $\theta$ commutes with the modular action of
$\theta$ commutes with the modular action of ![]() $\varphi$, the continuous core of
$\varphi$, the continuous core of ![]() $\widetilde {M}$ is such that
$\widetilde {M}$ is such that
where ![]() $\theta \colon G\curvearrowright C_\varphi (M)$ on the right-hand side is the canonical extension.
$\theta \colon G\curvearrowright C_\varphi (M)$ on the right-hand side is the canonical extension.
The next claim is important to us.
Claim We have ![]() $M'\cap C_\varphi (\widetilde {M}) = \mathbb {C}$.
$M'\cap C_\varphi (\widetilde {M}) = \mathbb {C}$.
Proof of Claim Since the canonical extension ![]() $\theta \colon G\curvearrowright C_\varphi (M)$ is still outer (e.g. [Reference TakesakiTak03, Lemma XII.6.14]), the crossed product
$\theta \colon G\curvearrowright C_\varphi (M)$ is still outer (e.g. [Reference TakesakiTak03, Lemma XII.6.14]), the crossed product ![]() $C_\varphi (M)\rtimes _\theta G$ is a factor. Let
$C_\varphi (M)\rtimes _\theta G$ is a factor. Let ![]() $E:= \varphi \otimes {\text { id}}\colon \mathbb {B}(L^2(M)) \mathbin {\overline {\otimes }} \mathbb {B}(L^2(G\times \mathbb {R})) \to \mathbb {B}(L^2(G\times \mathbb {R}))$, where
$E:= \varphi \otimes {\text { id}}\colon \mathbb {B}(L^2(M)) \mathbin {\overline {\otimes }} \mathbb {B}(L^2(G\times \mathbb {R})) \to \mathbb {B}(L^2(G\times \mathbb {R}))$, where ![]() $\varphi$ is extended to a normal state on
$\varphi$ is extended to a normal state on ![]() $\mathbb {B}(L^2(M))$, and observe that it restricts to a conditional expectation
$\mathbb {B}(L^2(M))$, and observe that it restricts to a conditional expectation ![]() $M\rtimes (G\times \mathbb {R}) \to L(G\times \mathbb {R})$ (because
$M\rtimes (G\times \mathbb {R}) \to L(G\times \mathbb {R})$ (because ![]() $\theta$ and
$\theta$ and ![]() $\sigma ^\varphi$ preserve
$\sigma ^\varphi$ preserve ![]() $\varphi$).
$\varphi$).
Since the ![]() $G\times \mathbb {R}$ action is trivial on
$G\times \mathbb {R}$ action is trivial on ![]() $M_{\varphi }$, we have that
$M_{\varphi }$, we have that
We have ![]() $E(x)=x$ for all
$E(x)=x$ for all ![]() $x\in M_{\varphi }'\cap C_\varphi (\widetilde {M})$, so that
$x\in M_{\varphi }'\cap C_\varphi (\widetilde {M})$, so that ![]() $M_{\varphi }'\cap C_\varphi (\widetilde {M})=L(G\times \mathbb {R})$. Then since
$M_{\varphi }'\cap C_\varphi (\widetilde {M})=L(G\times \mathbb {R})$. Then since ![]() $G\times \mathbb {R}$ is abelian,
$G\times \mathbb {R}$ is abelian,
Since ![]() $C_\varphi (\widetilde {M})$ is a factor, the conclusion follows.
$C_\varphi (\widetilde {M})$ is a factor, the conclusion follows.
To finish the proof, we have to show ![]() $k=1$. For this, suppose by contradiction that
$k=1$. For this, suppose by contradiction that ![]() $k\neq 1$ and
$k\neq 1$ and ![]() $G=\mathbb {Z}/k\mathbb {Z}$ is a nontrivial group. Then observe that the inclusion
$G=\mathbb {Z}/k\mathbb {Z}$ is a nontrivial group. Then observe that the inclusion ![]() $M\subset \widetilde {M}$ is with expectation, regular,
$M\subset \widetilde {M}$ is with expectation, regular, ![]() $\mathrm {BC}_\varphi (M)=\mathbb {C}$, and
$\mathrm {BC}_\varphi (M)=\mathbb {C}$, and ![]() $M'\cap C_\varphi (\widetilde {M})\subset C_\varphi (M)$. Hence we can apply Theorem 2.5 and get that
$M'\cap C_\varphi (\widetilde {M})\subset C_\varphi (M)$. Hence we can apply Theorem 2.5 and get that ![]() $\mathrm {BC}_\varphi (M\subset \widetilde {M}) =\mathbb {C}$. Since
$\mathrm {BC}_\varphi (M\subset \widetilde {M}) =\mathbb {C}$. Since ![]() $G$ is nontrivial,
$G$ is nontrivial, ![]() $1\in G$ (the image of
$1\in G$ (the image of ![]() $1\in \mathbb {Z}$ in
$1\in \mathbb {Z}$ in ![]() $G$) is nontrivial. We denote by
$G$) is nontrivial. We denote by ![]() $\lambda _1^G\in LG$ the canonical unitary corresponding to
$\lambda _1^G\in LG$ the canonical unitary corresponding to ![]() $1\in G$. Then since
$1\in G$. Then since ![]() $\theta ^\omega ={\text { id}}$ on
$\theta ^\omega ={\text { id}}$ on ![]() $(M^\omega )_{\varphi ^\omega }$ and since
$(M^\omega )_{\varphi ^\omega }$ and since ![]() $\operatorname {Ad}(\lambda _1^G)\in \operatorname {Aut}(\widetilde {M})$ coincides with
$\operatorname {Ad}(\lambda _1^G)\in \operatorname {Aut}(\widetilde {M})$ coincides with ![]() $\theta$ on
$\theta$ on ![]() $M$, we get
$M$, we get
This is a contradiction because ![]() $1\in G$ is nontrivial. Thus we get
$1\in G$ is nontrivial. Thus we get ![]() $k=1$ and this finishes the proof.
$k=1$ and this finishes the proof.
Appendix A. Popa's  $\mathcal {G}$-singular MASAs in type
$\mathcal {G}$-singular MASAs in type  ${\rm III_1}$ factors
${\rm III_1}$ factors
The following theorem is an analogue of [Reference PopaPop83, Theorem 4.2] in the type III setting. It covers the case that ![]() $M$ is a type
$M$ is a type ![]() ${\rm II_1}$ factor, a type
${\rm II_1}$ factor, a type ![]() ${\rm III}_\lambda$ factor
${\rm III}_\lambda$ factor ![]() $(0<\lambda <1)$, or a type
$(0<\lambda <1)$, or a type ![]() ${\rm III_1}$ factor with trivial bicentralizer. The proof is a rather straightforward adaptation of [Reference PopaPop16, Reference Houdayer and PopaHP17], so we merely sketch it.
${\rm III_1}$ factor with trivial bicentralizer. The proof is a rather straightforward adaptation of [Reference PopaPop16, Reference Houdayer and PopaHP17], so we merely sketch it.
Theorem A.1 Let ![]() $M$ be a factor with separable predual and
$M$ be a factor with separable predual and ![]() $\varphi \in M_\ast$ a faithful state such that
$\varphi \in M_\ast$ a faithful state such that ![]() $M_\varphi '\cap M=\mathbb {C}$. Let
$M_\varphi '\cap M=\mathbb {C}$. Let ![]() $\{\theta _n\}_{n\geq 1}\subset \operatorname {Aut}(M)$ be a countable subset such that
$\{\theta _n\}_{n\geq 1}\subset \operatorname {Aut}(M)$ be a countable subset such that
for all ![]() $n\geq 1$. Put
$n\geq 1$. Put ![]() $\theta _0:={\text { id}}_M$ and
$\theta _0:={\text { id}}_M$ and ![]() $\mathcal {G}:=\{\theta _n\}_{n\geq 0}$.
$\mathcal {G}:=\{\theta _n\}_{n\geq 0}$.
Then there is an abelian von Neumann subalgebra ![]() $A\subset M_\varphi$ such that
$A\subset M_\varphi$ such that ![]() $A$ is a MASA in
$A$ is a MASA in ![]() $M$ and that
$M$ and that ![]() $A$ is
$A$ is ![]() $\mathcal {G}$-singular in the following sense: if
$\mathcal {G}$-singular in the following sense: if ![]() $\theta \in \mathcal {G}$ satisfies
$\theta \in \mathcal {G}$ satisfies
for some nonzero projection ![]() $p\in A$ and
$p\in A$ and ![]() $u\in \mathcal {U}(M)$, then
$u\in \mathcal {U}(M)$, then ![]() $\theta ={\text { id}}_M$ and
$\theta ={\text { id}}_M$ and ![]() $up=pu\in A$.
$up=pu\in A$.
We note that, since ![]() ${\text { id}}_M$ is contained in
${\text { id}}_M$ is contained in ![]() $\mathcal {G}$, the resulting MASA
$\mathcal {G}$, the resulting MASA ![]() $A\subset M$ is singular in the sense that
$A\subset M$ is singular in the sense that ![]() $uAu^*=A$ for
$uAu^*=A$ for ![]() $u\in \mathcal {U}(M)$ implies
$u\in \mathcal {U}(M)$ implies ![]() $u\in A$.
$u\in A$.
The next lemma is a variant of [Reference PopaPop16, Lemma 1.2.2].
Lemma A.2 Let ![]() $M$ be a von Neumann algebra,
$M$ be a von Neumann algebra, ![]() $\varphi \in M_\ast$ a faithful normal state, and
$\varphi \in M_\ast$ a faithful normal state, and ![]() $N\subset M_\varphi$ a diffuse von Neumann subalgebra. Then for every finite-dimensional abelian von Neumann subalgebra
$N\subset M_\varphi$ a diffuse von Neumann subalgebra. Then for every finite-dimensional abelian von Neumann subalgebra ![]() $D\subset N$, finite subset
$D\subset N$, finite subset ![]() $X\subset M$, and
$X\subset M$, and ![]() $\varepsilon >0$, there exists a finite-dimensional abelian von Neumann subalgebra
$\varepsilon >0$, there exists a finite-dimensional abelian von Neumann subalgebra ![]() $A\subset N$ containing
$A\subset N$ containing ![]() $D$ such that
$D$ such that
Proof. If ![]() $M$ is a finite von Neumann algebra, this is an equivalent form of the last statement of [Reference PopaPop16, Lemma 1.2.2]. For a general
$M$ is a finite von Neumann algebra, this is an equivalent form of the last statement of [Reference PopaPop16, Lemma 1.2.2]. For a general ![]() $M$, since
$M$, since ![]() $N$ is contained in
$N$ is contained in ![]() $M_\varphi$, we can use [Reference PopaPop95, Theorem A.1.2] and then follow the proof of [Reference PopaPop16, Lemma 1.2.2].
$M_\varphi$, we can use [Reference PopaPop95, Theorem A.1.2] and then follow the proof of [Reference PopaPop16, Lemma 1.2.2].
Proof of Theorem A.1 We fix the following setting.
• Let
 $M$ be a von Neumann algebra with separable predual,
$M$ be a von Neumann algebra with separable predual,  $\varphi \in M_\ast$ a faithful state, and
$\varphi \in M_\ast$ a faithful state, and  $N\subset M_\varphi$ a type
$N\subset M_\varphi$ a type  ${\rm II}$ von Neumann subalgebra such that
${\rm II}$ von Neumann subalgebra such that  $N'\cap M\subset N$. Set
$N'\cap M\subset N$. Set
 \[ \operatorname{Aut}_\varphi(N\subset M):= \{ \theta\in \operatorname{Aut}(M)\mid \theta(\varphi)=\varphi,\ \theta(N)=N \} . \]
\[ \operatorname{Aut}_\varphi(N\subset M):= \{ \theta\in \operatorname{Aut}(M)\mid \theta(\varphi)=\varphi,\ \theta(N)=N \} . \]
• Let
 $\{\theta _n\}_{n\geq 1}\subset \operatorname {Aut}_\varphi (N\subset M)$ be such that
where
$\{\theta _n\}_{n\geq 1}\subset \operatorname {Aut}_\varphi (N\subset M)$ be such that
where \[ \iota_{n}(N)'\cap (M\otimes \mathbb{M}_2)\subset M\oplus M, \quad \text{for all }n\geq 1, \]
\[ \iota_{n}(N)'\cap (M\otimes \mathbb{M}_2)\subset M\oplus M, \quad \text{for all }n\geq 1, \]
 $\iota _n:=\iota _{\theta _n}$ is as in Lemma 2.3.
$\iota _n:=\iota _{\theta _n}$ is as in Lemma 2.3.
We will find ![]() $A\subset N$ that satisfies the conclusion of Theorem A.1 for
$A\subset N$ that satisfies the conclusion of Theorem A.1 for ![]() $\mathcal {G}=\{\theta _n\}_{n\geq 0}$ with
$\mathcal {G}=\{\theta _n\}_{n\geq 0}$ with ![]() $\theta _0={\text { id}}$. Thanks to Lemma 2.3, this gives the proof of Theorem A.1.
$\theta _0={\text { id}}$. Thanks to Lemma 2.3, this gives the proof of Theorem A.1.
For a von Neumann subalgebra ![]() $B\subset M$ that is globally invariant by
$B\subset M$ that is globally invariant by ![]() $\sigma ^\varphi$, we denote by
$\sigma ^\varphi$, we denote by ![]() $E_B\colon M\to B$ the unique
$E_B\colon M\to B$ the unique ![]() $\varphi$-preserving conditional expectation, and by
$\varphi$-preserving conditional expectation, and by ![]() $e_N$ the corresponding Jones projection.
$e_N$ the corresponding Jones projection.
Lemma A.3 Retain the setting of the above proof. We fix a finite-dimensional abelian von Neumann subalgebra ![]() $A\subset N$, a projection
$A\subset N$, a projection ![]() $f\in A'\cap N$, and finite subsets
$f\in A'\cap N$, and finite subsets ![]() $X\subset M$ and
$X\subset M$ and ![]() $Y\subset \operatorname {Aut}_\varphi (N\subset M)$. Then, for each
$Y\subset \operatorname {Aut}_\varphi (N\subset M)$. Then, for each ![]() $\varepsilon >0$, there exist a finite-dimensional abelian von Neumann subalgebra
$\varepsilon >0$, there exist a finite-dimensional abelian von Neumann subalgebra ![]() $D\subset N$, which contains
$D\subset N$, which contains ![]() $A$ and
$A$ and ![]() $f$, and
$f$, and ![]() $v \in \mathcal {U}(Df)$ such that
$v \in \mathcal {U}(Df)$ such that
Proof. Since ![]() $A\vee \mathbb {C} f \subset N$ is finite-dimensional, by [Reference PopaPop81, Theorem 3.3] (see also [Reference Houdayer and PopaHP17, Lemma 2.2]), there is a commutative von Neumann subalgebra
$A\vee \mathbb {C} f \subset N$ is finite-dimensional, by [Reference PopaPop81, Theorem 3.3] (see also [Reference Houdayer and PopaHP17, Lemma 2.2]), there is a commutative von Neumann subalgebra ![]() $B\subset N$ that is a MASA in
$B\subset N$ that is a MASA in ![]() $M$ and that contains
$M$ and that contains ![]() $A\vee \mathbb {C} f$. We can write
$A\vee \mathbb {C} f$. We can write ![]() $B=\bigvee _k B_k$, where
$B=\bigvee _k B_k$, where ![]() $\{B_k\}_k$ is an increasing sequence of finite-dimensional von Neumann algebras such that
$\{B_k\}_k$ is an increasing sequence of finite-dimensional von Neumann algebras such that ![]() $B_0:=A\vee \mathbb {C} f$.
$B_0:=A\vee \mathbb {C} f$.
Since ![]() $A_f'\cap N_f$ is of type
$A_f'\cap N_f$ is of type ![]() ${\rm II}$ and
${\rm II}$ and ![]() $B$ is of type I, we have
$B$ is of type I, we have
By Lemma 2.9, take ![]() $v\in \mathcal {U}(A_f'\cap N_f)$ such that for all
$v\in \mathcal {U}(A_f'\cap N_f)$ such that for all ![]() $\theta \in Y$,
$\theta \in Y$,
By approximating ![]() $v$ by finite sums of projections, we may assume that
$v$ by finite sums of projections, we may assume that ![]() $v$ is contained in a finite-dimensional abelian subalgebra in
$v$ is contained in a finite-dimensional abelian subalgebra in ![]() $A_f'\cap N_f$. Hence there exists a finite-dimensional commutative von Neumann algebra
$A_f'\cap N_f$. Hence there exists a finite-dimensional commutative von Neumann algebra ![]() $D_1 \subset N_f$ containing
$D_1 \subset N_f$ containing ![]() $v$ and
$v$ and ![]() $A_f$.
$A_f$.
Since ![]() $e_{B_k'\cap M } \to e_{B'\cap M} = e_{B}$ strongly, there exists
$e_{B_k'\cap M } \to e_{B'\cap M} = e_{B}$ strongly, there exists ![]() $k$ such that
$k$ such that
Here we can exchange ![]() $E_{B_k'\cap M }$ by
$E_{B_k'\cap M }$ by ![]() $E_{D_2'\cap M_{f^\perp } }$, where
$E_{D_2'\cap M_{f^\perp } }$, where ![]() $D_2:=(B_k)_{f^\perp }$. Then
$D_2:=(B_k)_{f^\perp }$. Then ![]() $D:=D_1\oplus D_2 \subset N_f \oplus N_{f^\perp }\subset N$ works.
$D:=D_1\oplus D_2 \subset N_f \oplus N_{f^\perp }\subset N$ works.
Take a ![]() $\ast$-strongly dense subset
$\ast$-strongly dense subset ![]() $\{x_n\}_{n\in \mathbb {N}}\subset (M)_1$. Take projections
$\{x_n\}_{n\in \mathbb {N}}\subset (M)_1$. Take projections ![]() $\{e_n\}_{n\in \mathbb {N}}$ in
$\{e_n\}_{n\in \mathbb {N}}$ in ![]() $N$ which are
$N$ which are ![]() $\ast$-strongly dense in all projections in
$\ast$-strongly dense in all projections in ![]() $N$. We may assume that
$N$. We may assume that ![]() $e_0=x_0=1$ and that each
$e_0=x_0=1$ and that each ![]() $e_k$ appears infinitely many times in
$e_k$ appears infinitely many times in ![]() $\{e_n\}_{n\in \mathbb {N}}$.
$\{e_n\}_{n\in \mathbb {N}}$.
For each ![]() $n>0$, we denote the inclusion
$n>0$, we denote the inclusion ![]() $\iota _n(M)\subset M\otimes \mathbb {M}_2$ by
$\iota _n(M)\subset M\otimes \mathbb {M}_2$ by ![]() $M\subset M_n$. For
$M\subset M_n$. For ![]() $n=0$, we put
$n=0$, we put ![]() $M_0:=M$.
$M_0:=M$.
Claim There exist an increasing sequence of finite-dimensional von Neumann abelian subalgebras ![]() $A_n\subset N$, projections
$A_n\subset N$, projections ![]() $f_n\in A_n$, and unitaries
$f_n\in A_n$, and unitaries ![]() $v_n \in \mathcal {U}(A_nf_n)$ such that
$v_n \in \mathcal {U}(A_nf_n)$ such that
(P1)
 $\|f_n - e_n\|_\varphi \leq 7 \| e_n-E_{A_{n-1}'\cap N}(e_n) \|_\varphi$,
$\|f_n - e_n\|_\varphi \leq 7 \| e_n-E_{A_{n-1}'\cap N}(e_n) \|_\varphi$,(P2)
 $\| E_{A_{n}'\cap M}( x_i^* \theta _k(v_n) x_j )f_n^\perp \|_{\varphi }\leq 1/n$ for all
$\| E_{A_{n}'\cap M}( x_i^* \theta _k(v_n) x_j )f_n^\perp \|_{\varphi }\leq 1/n$ for all  $0\leq i,j,k\leq n$,
$0\leq i,j,k\leq n$,(P3)
 $\| E_{A_{n}'\cap M}(x_j) - E_{A_n}(x_j) \|_{\varphi }\leq 1/n$ for all
$\| E_{A_{n}'\cap M}(x_j) - E_{A_n}(x_j) \|_{\varphi }\leq 1/n$ for all  $0\leq j\leq n$,
$0\leq j\leq n$,(P4)
 $\| E_{A_{n}'\cap M_k}(x_j) - E_{A_n\vee (N'\cap M_k)}(x_j) \|_{\varphi }\leq 1/n$ for all
$\| E_{A_{n}'\cap M_k}(x_j) - E_{A_n\vee (N'\cap M_k)}(x_j) \|_{\varphi }\leq 1/n$ for all  $0\leq j\leq n$ and
$0\leq j\leq n$ and  $1\leq k\leq n$.
$1\leq k\leq n$.
Proof. Suppose that ![]() $(A_k,f_k,v_k)$ are constructed for
$(A_k,f_k,v_k)$ are constructed for ![]() $0\leq k \leq n$, and we will construct one for
$0\leq k \leq n$, and we will construct one for ![]() $k=n+1$. Following the proof of the first part of [Reference Houdayer and PopaHP17, Theorem 1], by using Lemma A.3, one can construct
$k=n+1$. Following the proof of the first part of [Reference Houdayer and PopaHP17, Theorem 1], by using Lemma A.3, one can construct ![]() $(A_{n+1},f_{n+1},v_{n+1})$ that satisfies (P1), (P2), and (P3). To see (P4), we put
$(A_{n+1},f_{n+1},v_{n+1})$ that satisfies (P1), (P2), and (P3). To see (P4), we put ![]() $D_{n+1} := A_{n+1}$, and below we construct
$D_{n+1} := A_{n+1}$, and below we construct ![]() $A_{n+1}$ that satisfies all the desired conditions.
$A_{n+1}$ that satisfies all the desired conditions.
We apply Lemma A.2 and find an abelian von Neumann subalgebra ![]() $B_{n+1}^0\subset N$ containing
$B_{n+1}^0\subset N$ containing ![]() $D_{n+1}$ such that
$D_{n+1}$ such that
Next we again apply Lemma A.2 and find an abelian von Neumann subalgebra ![]() $B^1_{n+1}\subset N$ containing
$B^1_{n+1}\subset N$ containing ![]() $B_{n+1}^0$ such that the same inequality holds for the inclusion
$B_{n+1}^0$ such that the same inequality holds for the inclusion ![]() $B^1_{n+1}\subset N\subset M_1$. We repeat this procedure and construct
$B^1_{n+1}\subset N\subset M_1$. We repeat this procedure and construct ![]() $B^k_{n+1}\subset N$ containing
$B^k_{n+1}\subset N$ containing ![]() $B_{n+1}^{k-1}$ such that
$B_{n+1}^{k-1}$ such that
Put ![]() $A_{n+1}:=B_{n+1}^{n+1}$. Then since the corresponding Jones projections satisfy
$A_{n+1}:=B_{n+1}^{n+1}$. Then since the corresponding Jones projections satisfy
for all ![]() $0\leq k\leq n+1$,
$0\leq k\leq n+1$, ![]() $A_{n+1}$ satisfies (P4).
$A_{n+1}$ satisfies (P4).
We next check (P1), (P2), and (P3) for this new ![]() $A_{n+1}$. We do not use
$A_{n+1}$. We do not use ![]() $A_{n+1}$ in (P1), hence it automatically holds. Regarding (P2) and (P3), since
$A_{n+1}$ in (P1), hence it automatically holds. Regarding (P2) and (P3), since ![]() $D_{n+1}\subset A_{n+1}$, one has
$D_{n+1}\subset A_{n+1}$, one has
so that (P2) and (P3) still hold for ![]() $A_{n+1}$.
$A_{n+1}$.
Take ![]() $A_n$ as in the claim, and define
$A_n$ as in the claim, and define ![]() $A := \bigvee _n A_n \subset N$. Then (P3) and (P4) imply that
$A := \bigvee _n A_n \subset N$. Then (P3) and (P4) imply that ![]() $A$ is a MASA in
$A$ is a MASA in ![]() $M$ and that
$M$ and that
We will show that ![]() $A$ satisfies the conclusion of Theorem A.1.
$A$ satisfies the conclusion of Theorem A.1.
Suppose now that there exist ![]() $\theta \in \mathcal {G}$,
$\theta \in \mathcal {G}$, ![]() $u\in \mathcal {U}(M)$, and a nonzero projection
$u\in \mathcal {U}(M)$, and a nonzero projection ![]() $p\in A$ such that
$p\in A$ such that
Since ![]() $A,\theta ^u(A)$ are MASAs in
$A,\theta ^u(A)$ are MASAs in ![]() $M$, putting
$M$, putting ![]() $q:=\theta ^u(p)\in A$, we have a
$q:=\theta ^u(p)\in A$, we have a ![]() $\ast$-isomorphism
$\ast$-isomorphism
Assume first ![]() $\theta ={\text { id}}$ and
$\theta ={\text { id}}$ and ![]() $\theta ^u|_{Ap}={\text { id}}_{Ap}$. Then since
$\theta ^u|_{Ap}={\text { id}}_{Ap}$. Then since ![]() $A$ is a MASA in
$A$ is a MASA in ![]() $M$, we get
$M$, we get ![]() $up=pu\in A$, which is the conclusion. So from now on, we assume either that
$up=pu\in A$, which is the conclusion. So from now on, we assume either that ![]() $\theta \neq {\text { id}}$, or
$\theta \neq {\text { id}}$, or ![]() $\theta ={\text { id}}$ and
$\theta ={\text { id}}$ and ![]() $\theta ^u|_{Ap}\neq {\text { id}}_{Ap}$. Then we will deduce a contradiction.
$\theta ^u|_{Ap}\neq {\text { id}}_{Ap}$. Then we will deduce a contradiction.
Claim There exists a nonzero projection ![]() $z\in Ap$ such that
$z\in Ap$ such that ![]() $\theta ^u(z)z=0$.
$\theta ^u(z)z=0$.
Proof. If ![]() $\theta = \theta _n$
$\theta = \theta _n$ ![]() $(n\geq 1)$ and
$(n\geq 1)$ and ![]() $\theta ^u|_{Ap} = {\text { id}}_{Ap}$, then
$\theta ^u|_{Ap} = {\text { id}}_{Ap}$, then ![]() $\big [{\kern-1.3pt}\begin{smallmatrix} 0 & pu \\ 0 & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in
$\big [{\kern-1.3pt}\begin{smallmatrix} 0 & pu \\ 0 & 0 \end{smallmatrix}{\kern-1.3pt}\big ]$ is contained in ![]() $A'\cap M_n \subset M\oplus M$, hence we have a contradiction. So we have
$A'\cap M_n \subset M\oplus M$, hence we have a contradiction. So we have ![]() $\theta ^u|_{Ap} \neq {\text { id}}_{Ap}$ in this case. The same holds if
$\theta ^u|_{Ap} \neq {\text { id}}_{Ap}$ in this case. The same holds if ![]() $\theta =\theta _0={\text { id}}_M$ by assumption.
$\theta =\theta _0={\text { id}}_M$ by assumption.
Put ![]() $q:=\theta ^u(p)$. If
$q:=\theta ^u(p)$. If ![]() $p=q$, then
$p=q$, then ![]() $\theta ^u$ defines a nontrivial automorphism on
$\theta ^u$ defines a nontrivial automorphism on ![]() $Ap$, so that
$Ap$, so that ![]() $z\in Ap$ exists. If
$z\in Ap$ exists. If ![]() $p\neq q$, then, putting
$p\neq q$, then, putting ![]() $z_0:=p-pq\in Ap$ and
$z_0:=p-pq\in Ap$ and ![]() $w_0:=q-pq\in Aq$, we have
$w_0:=q-pq\in Aq$, we have ![]() $z_0\neq 0$ or
$z_0\neq 0$ or ![]() $w_0\neq 0$. If
$w_0\neq 0$. If ![]() $z_0\neq 0$, then
$z_0\neq 0$, then ![]() $z:=z_0$ works. If
$z:=z_0$ works. If ![]() $w_0\neq 0$, then
$w_0\neq 0$, then ![]() $z:=(\theta ^u)^{-1}(w_0)$ works.
$z:=(\theta ^u)^{-1}(w_0)$ works.
We apply Lemma 2.1(3) to ![]() $A\subset M$ and
$A\subset M$ and ![]() $(\theta ^u)^{-1} \colon qMq \to pMp$ with
$(\theta ^u)^{-1} \colon qMq \to pMp$ with ![]() $(\theta ^u)^{-1}(Aq)=Ap$. By using
$(\theta ^u)^{-1}(Aq)=Ap$. By using ![]() $(\theta ^u)^{-1}=\operatorname {Ad}(\theta ^{-1}(u^*))\circ \theta ^{-1}$ and
$(\theta ^u)^{-1}=\operatorname {Ad}(\theta ^{-1}(u^*))\circ \theta ^{-1}$ and ![]() $\theta (\varphi )=\varphi$, there is a unique nonsingular positive self-adjoint element
$\theta (\varphi )=\varphi$, there is a unique nonsingular positive self-adjoint element ![]() $h$, which is affiliated with
$h$, which is affiliated with ![]() $Ap$, such that
$Ap$, such that
There exists a spectral projection ![]() $p_0\in Ap$ of
$p_0\in Ap$ of ![]() $h$ such that
$h$ such that
To deduce a contradiction, up to replacing ![]() $p,z,q$ by
$p,z,q$ by ![]() $p_0,zp_0,\theta ^u(p_0)$, we may assume
$p_0,zp_0,\theta ^u(p_0)$, we may assume ![]() $p=p_0$ (while still
$p=p_0$ (while still ![]() $z\leq p$). Then
$z\leq p$). Then ![]() $u\theta (z)$ is a partial isometry, for which there are
$u\theta (z)$ is a partial isometry, for which there are ![]() $\kappa _1,\kappa _2>0$ such that
$\kappa _1,\kappa _2>0$ such that
Claim The following assertions hold.
(a)
 \begin{align*}&&\|z f_n\|_\varphi &= \|\theta(v_nz)\|_\varphi\leq \kappa_1 \|E_{A_n'\cap M}(u \theta(v_nz) u^*)z^\perp \|_\varphi,\quad \text{for all}\ n\in \mathbb{N}; &&\end{align*}
\begin{align*}&&\|z f_n\|_\varphi &= \|\theta(v_nz)\|_\varphi\leq \kappa_1 \|E_{A_n'\cap M}(u \theta(v_nz) u^*)z^\perp \|_\varphi,\quad \text{for all}\ n\in \mathbb{N}; &&\end{align*}(b)
 \begin{align*}&& \|E_{A_n'\cap M}(u \theta(v_n z)u^*)z^\perp \|_\varphi &\leq \|E_{A_n'\cap M}( x \theta(v_n) y)z^\perp \|_\varphi + \kappa_2 \| u-x \|_\varphi &&\\ &&&\quad +\|x\| \| \theta(z)u^* - y\|_\varphi,\quad \text{for all}\ x,y\in M\ \text{and}\ n\in \mathbb{N}; &&\end{align*}
\begin{align*}&& \|E_{A_n'\cap M}(u \theta(v_n z)u^*)z^\perp \|_\varphi &\leq \|E_{A_n'\cap M}( x \theta(v_n) y)z^\perp \|_\varphi + \kappa_2 \| u-x \|_\varphi &&\\ &&&\quad +\|x\| \| \theta(z)u^* - y\|_\varphi,\quad \text{for all}\ x,y\in M\ \text{and}\ n\in \mathbb{N}; &&\end{align*}(c)
 \begin{align*}&&\|e_n - f_n\|_\varphi &\leq 7\|e_n-z\|_\varphi,\quad \text{for all}\ n\in \mathbb{N}. &&\end{align*}
\begin{align*}&&\|e_n - f_n\|_\varphi &\leq 7\|e_n-z\|_\varphi,\quad \text{for all}\ n\in \mathbb{N}. &&\end{align*}
Proof. We have only to follow arguments in [Reference Houdayer and PopaHP17, Theorem 1], but we give proofs for the reader's convenience. We explain only (a) and (c), since (b) is straightforward.
For (a), since ![]() $zf_n=f_nz$,
$zf_n=f_nz$, ![]() $v_n^*v_n = f_n$ and
$v_n^*v_n = f_n$ and ![]() $\theta (\varphi )=\varphi$,
$\theta (\varphi )=\varphi$,
Then since ![]() $u\theta (v_n z)u^* = \theta ^u(v_nz)\theta ^u(z)$,
$u\theta (v_n z)u^* = \theta ^u(v_nz)\theta ^u(z)$, ![]() $z\theta ^u(z)=0$, and
$z\theta ^u(z)=0$, and ![]() $\theta ^u(v_nz) \in Aq \subset A'\cap M$, one has
$\theta ^u(v_nz) \in Aq \subset A'\cap M$, one has
We thus have (a).
For (c), since ![]() $z\in A\subset A_{n-1}'\cap N$, combined with (P1), one has
$z\in A\subset A_{n-1}'\cap N$, combined with (P1), one has
We thus have (c).
Take a subsequence ![]() $\{n_k\}_k$ such that
$\{n_k\}_k$ such that ![]() $e_{n_k} \to z$ strongly. Then (c) implies that
$e_{n_k} \to z$ strongly. Then (c) implies that ![]() $e_{n_k} - f_{n_k}$ converges to
$e_{n_k} - f_{n_k}$ converges to ![]() $0$ strongly, so that
$0$ strongly, so that ![]() $zf_{n_k}\to z$ as well. We show that
$zf_{n_k}\to z$ as well. We show that ![]() $zf_{n_k}$ also converges to
$zf_{n_k}$ also converges to ![]() $0$, a contradiction.
$0$, a contradiction.
Fix ![]() $\varepsilon >0$ and take
$\varepsilon >0$ and take ![]() $x_i,x_j$ such that
$x_i,x_j$ such that ![]() $\kappa _2\| u-x_i^* \|_\varphi + \| \theta (z)u^* - x_j\|_\varphi <\varepsilon$. Then by (a) and (b),
$\kappa _2\| u-x_i^* \|_\varphi + \| \theta (z)u^* - x_j\|_\varphi <\varepsilon$. Then by (a) and (b),
 \begin{align*} \kappa_1^{-1}\|z f_n\|_\varphi &\leq \|E_{A_n'\cap M}(u \theta(v_n z) u^*)z^\perp \|_\varphi \\ &\leq \|E_{A_n'\cap M}( x_i^* \theta(v_n) x_j)z^\perp \|_\varphi + \varepsilon\\ &\leq \|E_{A_n'\cap M}( x_i^* \theta(v_n) x_j)f_n^\perp \|_\varphi + \|z^\perp - f_n^\perp\|_\varphi+ \varepsilon. \end{align*}
\begin{align*} \kappa_1^{-1}\|z f_n\|_\varphi &\leq \|E_{A_n'\cap M}(u \theta(v_n z) u^*)z^\perp \|_\varphi \\ &\leq \|E_{A_n'\cap M}( x_i^* \theta(v_n) x_j)z^\perp \|_\varphi + \varepsilon\\ &\leq \|E_{A_n'\cap M}( x_i^* \theta(v_n) x_j)f_n^\perp \|_\varphi + \|z^\perp - f_n^\perp\|_\varphi+ \varepsilon. \end{align*}
Then (P2) implies
Letting ![]() $\varepsilon \to 0$, we get
$\varepsilon \to 0$, we get ![]() $zf_{n_k}\to 0$ strongly, as desired.
$zf_{n_k}\to 0$ strongly, as desired.
Acknowledgements
The author would like to thank Yuki Arano, Toshihiko Masuda, and Reiji Tomatsu for fruitful conversations about automorphisms of von Neumann algebras. He also would like to thank Amine Marrakchi for letting him know about the recent work on relative bicentralizers.
Conflicts of interest
None
Financial support
The author is supported by JSPS KAKENHI Grant Number 20K14324.
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.