Article contents
Frobenius fields for Drinfeld modules of rank 2
Published online by Cambridge University Press: 01 July 2008
Abstract
Let ϕ be a Drinfeld module of rank 2 over the field of rational functions 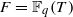 , with
, with 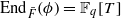 . Let K be a fixed imaginary quadratic field over F and d a positive integer. For each prime
. Let K be a fixed imaginary quadratic field over F and d a positive integer. For each prime 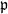 of good reduction for ϕ, let
of good reduction for ϕ, let 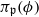 be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field
be a root of the characteristic polynomial of the Frobenius endomorphism of ϕ over the finite field 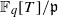 . Let Πϕ(K;d) be the number of primes
. Let Πϕ(K;d) be the number of primes 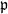 of degree d such that the field extension
of degree d such that the field extension 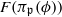 is the fixed imaginary quadratic field K. We present upper bounds for Πϕ(K;d) obtained by two different approaches, inspired by similar ones for elliptic curves. The first approach, inspired by the work of Serre, is to consider the image of Frobenius in a mixed Galois representation associated to K and to the Drinfeld module ϕ. The second approach, inspired by the work of Cojocaru, Fouvry and Murty, is based on an application of the square sieve. The bounds obtained with the first method are better, but depend on the fixed quadratic imaginary field K. In our application of the second approach, we improve the results of Cojocaru, Murty and Fouvry by considering projective Galois representations.
is the fixed imaginary quadratic field K. We present upper bounds for Πϕ(K;d) obtained by two different approaches, inspired by similar ones for elliptic curves. The first approach, inspired by the work of Serre, is to consider the image of Frobenius in a mixed Galois representation associated to K and to the Drinfeld module ϕ. The second approach, inspired by the work of Cojocaru, Fouvry and Murty, is based on an application of the square sieve. The bounds obtained with the first method are better, but depend on the fixed quadratic imaginary field K. In our application of the second approach, we improve the results of Cojocaru, Murty and Fouvry by considering projective Galois representations.
Keywords
MSC classification
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2008
References
The first author is supported in part by NSF grant DMS-0636750, and the second author is supported in part by a NSERC Discovery Grant.
- 4
- Cited by


