Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T00:43:52.178Z Has data issue: false hasContentIssue false
  • English
  • Français

Compactifications of reductive groups as moduli stacks of bundles

Part of: Semigroups Special varieties Linear algebraic groups and related topics Algebraic groups Families, fibrations Curves

Published online by Cambridge University Press:  18 August 2015

Johan Martens  and
Michael Thaddeus
Johan Martens
Affiliation:
School of Mathematics and Maxwell Institute, The University of Edinburgh, James Clerk Maxwell Building, Peter Guthrie Tait Road, Edinburgh EH9 3FD, Scotland email [email protected]
Michael Thaddeus
Affiliation:
Department of Mathematics, Columbia University, 2990 Broadway, New York, NY 10027, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 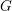$G$ be a split reductive group. We introduce the moduli problem of bundle chains parametrizing framed principal 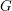$G$-bundles on chains of lines. Any fan supported in a Weyl chamber determines a stability condition on bundle chains. Its moduli stack provides an equivariant toroidal compactification of 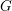$G$. All toric orbifolds may be thus obtained. Moreover, we get a canonical compactification of any semisimple 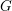$G$, which agrees with the wonderful compactification in the adjoint case, but which in other cases is an orbifold. Finally, we describe the connections with Losev–Manin’s spaces of weighted pointed curves and with Kausz’s compactification of 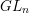$GL_{n}$.

Keywords

reductive groupscompactificationsmoduli problemsprincipal bundles

MSC classification

Primary: 14D23: Stacks and moduli problems
Secondary: 14H60: Vector bundles on curves and their moduli 14L30: Group actions on varieties or schemes (quotients) 14M27: Compactifications; symmetric and spherical varieties 20G15: Linear algebraic groups over arbitrary fields 20M32: Algebraic monoids
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 1 , January 2016 , pp. 62 - 98
Copyright
© The Authors 2015 

References

Abramovich, D., Corti, A. and Vistoli, A., Twisted bundles and admissible covers, Comm. Algebra 31 (2003), 3547–3618.CrossRefGoogle Scholar
Abramovich, D., Olsson, M. and Vistoli, A., Tame stacks in positive characteristic, Ann. Inst. Fourier (Grenoble) 58 (2008), 1057–1091.CrossRefGoogle Scholar
Alexeev, V. and Brion, M., Stable reductive varieties I: affine varieties, Invent. Math. 157 (2004), 227–274.CrossRefGoogle Scholar
Artin, M., Algebraization of formal moduli: I, in Global analysis: papers in honor of K. Kodaira, eds Spencer, D. C. and Iyanaga, S. (University of Tokyo and Princeton University Press, 1969), 21–71.Google Scholar
Artin, M., Versal deformations and algebraic stacks, Invent. Math. 27 (1974), 165–189.CrossRefGoogle Scholar
Batyrev, V. and Blume, M., On generalisations of Losev–Manin moduli spaces for classical root systems, Pure Appl. Math. Q. 7 (2011), 1053–1084; doi: 10.4310/PAMQ.2011.v7.n4.a2.CrossRefGoogle Scholar
Biswas, I. and Nagaraj, D. S., Principal bundles over the projective line, J. Algebra 322 (2009), 3478–3491.CrossRefGoogle Scholar
Borisov, L. A., Chen, L. and Smith, G. G., The orbifold Chow ring of toric Deligne–Mumford stacks, J. Amer. Math. Soc. 18 (2005), 193–215.CrossRefGoogle Scholar
Brion, M., The total coordinate ring of a wonderful variety, J. Algebra 313 (2007), 61–99.CrossRefGoogle Scholar
Brion, M., On automorphism groups of fiber bundles, Publ. Mat. Urug. 12 (2011), 39–66, arXiv:1012.4606.Google Scholar
Conrad, B., The Keel–Mori theorem via stacks, Preprint (2005),http://math.stanford.edu/∼conrad/papers/coarsespace.pdf.Google Scholar
Conrad, B., Gabber, O. and Prasad, G., Pseudo-reductive groups (Cambridge University Press, 2010).CrossRefGoogle Scholar
Cox, D. A., The homogeneous coordinate ring of a toric variety, J. Algebraic Geom. 4 (1995), 17–50.Google Scholar
Cox, D., Little, J. and Schenck, H., Toric varieties (American Mathematical Society, 2011).CrossRefGoogle Scholar
De Concini, C. and Procesi, C., Complete symmetric varieties, in Invariant theory (Montecatini, 1982), Lecture Notes in Mathematics, vol. 996 (Springer, 1983), 1–44.Google Scholar
De Concini, C. and Procesi, C., Complete symmetric varieties II: intersection theory, in Algebraic groups and related topics (Kyoto/Nagoya, 1983), Advanced Studies in Pure Mathematics, vol. 6 (North-Holland, 1985), 481–513.CrossRefGoogle Scholar
Deligne, P. and Mumford, D., The irreducibility of the space of curves of given genus, Publ. Math. Inst. Hautes Études Sci. 36 (1969), 75–109.CrossRefGoogle Scholar
Demazure, M. and Gabriel, P., Groupes algébriques (North-Holland, 1970).Google Scholar
Dolgachev, I., Lectures on invariant theory, London Mathematical Society Lecture Note Series, vol. 296 (Cambridge, 2003).CrossRefGoogle Scholar
Grothendieck, A., Eléments de géométrie algébrique, Publ. Math. Inst. Hautes Études Sci. 4 (1960), [vol. I], 8 (1961) [vol. II], 11 (1961), 17 (1963) [vol. III], 20 (1964), 24 (1965), 28 (1966), 32 (1967) [vol. IV].CrossRefGoogle Scholar
Evens, S. and Jones, B. F., On the wonderful compactification, Preprint (2008),arXiv:0801.0456.Google Scholar
Fantechi, B., Mann, E. and Nironi, F., Smooth toric Deligne–Mumford stacks, J. Reine Angew. Math. 648 (2010), 201–244.Google Scholar
Fulghesu, D., On the Chow ring of the stack of rational nodal curves, PhD thesis, Scuola Normale Superiore di Pisa (2005), http://fulghesu.eu/doc/tesi_perfezionamento.pdf.Google Scholar
Gieseker, D., A degeneration of the moduli space of stable bundles, J. Differential Geom. 19 (1984), 173–206.CrossRefGoogle Scholar
Grothendieck, A., Sur la classification des fibrés holomorphes sur la sphère de Riemann, Amer. J. Math. 79 (1957), 121–138.CrossRefGoogle Scholar
Gulbrandsen, M. G., Halle, L. H. and Hulek, K., A relative Hilbert–Mumford criterion, Manuscripta Math., to appear, doi:10.1007/s00229-015-0744-8.CrossRefGoogle Scholar
Hall, J., Moduli of singular curves, Preprint (2010), arXiv:1011.6007.Google Scholar
Harder, G., Halbeinfache gruppenschemata über vollständigen Kurven, Invent. Math. 6 (1968), 107–149.CrossRefGoogle Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, 1977).CrossRefGoogle Scholar
Hartshorne, R., Deformation theory, Graduate Texts in Mathematics, vol. 257 (Springer, 2010).CrossRefGoogle Scholar
Hassett, B., Moduli spaces of weighted pointed stable curves, Adv. Math. 173 (2003), 316–352.CrossRefGoogle Scholar
Hausel, T. and Sturmfels, B., Toric hyperkähler varieties, Doc. Math. 7 (2002), 495–534.CrossRefGoogle Scholar
Huruguen, M., Compactification d’espaces homogènes sphériques sur un corps quelconque, PhD thesis, Université de Grenoble (2011), http://tel.archives-ouvertes.fr/docs/00/71/64/02/PDF/24054_HURUGUEN_2011_archivage.pdf.Google Scholar
Huruguen, M., Toric varieties and spherical embeddings over an arbitrary field, J. Algebra 342 (2011), 212–234.CrossRefGoogle Scholar
Iwahori, N. and Matsumoto, H., On some Bruhat decomposition and the structure of the Hecke rings of p-adic Chevalley groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 5–48.CrossRefGoogle Scholar
de Jong, A. J. et al. , The stacks project, http://stacks.math.columbia.edu.Google Scholar
Kausz, I., A modular compactification of the general linear group, Doc. Math. 5 (2000), 553–594.CrossRefGoogle Scholar
Kausz, I., A Gieseker type degeneration of moduli stacks of vector bundles on curves, Trans. Amer. Math. Soc. 357 (2005), 4897–4955.CrossRefGoogle Scholar
Kempf, G., Knudsen, F., Mumford, D. and Saint-Donat, B., Toroidal embeddings I, Lecture Notes in Mathematics, vol. 339 (Springer, 1973).CrossRefGoogle Scholar
King, A., Moduli of representations of finite-dimensional algebras, Q. J. Math. (2) 45 (1994), 515–530.CrossRefGoogle Scholar
Kleiman, S. and Thorup, A., Complete bilinear forms, in Algebraic geometry (Sundance, UT, 1986), Lecture Notes in Mathematics, vol. 1311 (Springer, 1988).Google Scholar
Knutson, D., Algebraic spaces, Lecture Notes in Mathematics, vol. 203 (Springer, 1971).CrossRefGoogle Scholar
Kumar, S., Kac–Moody groups, their flag varieties and representation theory, Progress in Mathematics, vol. 204 (Birkhäuser, 2002).CrossRefGoogle Scholar
Laksov, D., Completed quadrics and linear maps, Algebraic geometry: Bowdoin 1985, Proceedings of Symposia in Pure Mathematics, vol. 46, Part 2, eds Bloch, Spencer et al. (American Mathematical Society, 1987), 321–370.Google Scholar
Laumon, G. and Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik, vol. 39 (Springer, 2000).CrossRefGoogle Scholar
Losev, A. and Manin, Y., New moduli spaces of pointed curves and pencils of flat connections, Michigan Math. J. 48 (2000), 443–472.CrossRefGoogle Scholar
Li, J., Stable morphisms to singular schemes and relative stable morphisms, J. Differential Geom. 57 (2001), 509–578.CrossRefGoogle Scholar
Martens, J. and Thaddeus, M., Variations on a theme of Grothendieck, Preprint (2012), arXiv:1210.8161.Google Scholar
Milne, J., Étale cohomology (Princeton University Press, 1980).Google Scholar
Nagaraj, D. S. and Seshadri, C. S., Degenerations of the moduli spaces of vector bundles on curves, II: Generalized Gieseker moduli spaces, Proc. Indian Acad. Sci. Math. Sci. 109 (1999), 165–201.CrossRefGoogle Scholar
Pezzini, G., Lectures on spherical and wonderful varieties, Les cours du CIRM 1 (2010), 33–53, ccirm.cedram.org/ccirm-bin/fitem?id=CCIRM_2010__1_1_33_0.CrossRefGoogle Scholar
Renner, L. E., Linear algebraic monoids, Encyclopaedia of Mathematical Sciences, vol. 134 (Springer, 2005).Google Scholar
Rittatore, A., Algebraic monoids and group embeddings, Transform. Groups 3 (1998), 375–396.CrossRefGoogle Scholar
Rittatore, A., Very flat reductive monoids, Publ. Mat. Urug. 9 (2001–2), 93–121.Google Scholar
Schmitt, A., The Hilbert compactification of the universal moduli space of semistable vector bundles over smooth curves, J. Differential Geom. 66 (2004), 169–209.CrossRefGoogle Scholar
Semple, J. G., On complete quadrics, J. Lond. Math. Soc. 23 (1948), 258–267.CrossRefGoogle Scholar
Semple, J. G., The variety whose points represent complete collineations of S r on S r′, Univ. Roma Ist. Naz. Alta Mat. Rend. Mat. e Appl. (5) 10 (1951), 201–208.Google Scholar
Semple, J. G., On complete quadrics, II, J. Lond. Math. Soc. 27 (1952), 280–287.CrossRefGoogle Scholar
Sernesi, E., Deformations of algebraic schemes, Grundlehren Math. Wiss., vol. 334 (Springer, 2006).Google Scholar
Springer, T. A., Some results on compactifications of semisimple groups, Proceedings of the International Congress of Mathematicians, vol. II (European Mathematical Society, Zürich, 2006), 1337–1348.Google Scholar
Steinberg, R., Regular elements of semi-simple algebraic groups, Publ. Math. Inst. Hautes Études Sci. 25 (1965), 49–80.CrossRefGoogle Scholar
Teodorescu, T., Principal bundles over chains or cycles of rational curves, Michigan Math. J. 50 (2002), 173–186.CrossRefGoogle Scholar
Thaddeus, M., Complete collineations revisited, Math. Ann. 315 (1999), 469–495.CrossRefGoogle Scholar
Timashev, D. A., Homogeneous spaces and equivariant embeddings, Encyclopaedia Math. Sci., vol. 138 (Springer, 2011).CrossRefGoogle Scholar
Vainsencher, I., Complete collineations and blowing up determinantal ideals, Math. Ann. 267 (1984), 417–432.CrossRefGoogle Scholar
Vinberg, E. B., On reductive algebraic semigroups, in Lie groups and Lie algebras: E.B. Dynkin’s Seminar, American Mathematical Society Translations: Series 2, vol. 169 (American Mathematical Society, 1995), 145–182.Google Scholar
Vistoli, A., Grothendieck topologies, fibered categories and descent theory, in Fundamental algebraic geometry: Grothendieck’s FGA explained, Mathematical Surveys and Monographs, vol. 123, eds Fantechi, B. et al. (American Mathematical Society, 2005).Google Scholar