Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T23:50:45.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Chern–Schwartz–MacPherson classes for Schubert cells in flag manifolds

Part of: Special varieties Projective and enumerative geometry Cycles and subschemes

Published online by Cambridge University Press:  14 November 2016

Paolo Aluffi  and
Leonardo C. Mihalcea
Paolo Aluffi
Affiliation:
Mathematics Department, Florida State University, Tallahassee, FL 32306, USA email [email protected]
Leonardo C. Mihalcea
Affiliation:
Department of Mathematics, Virginia Tech University, Blacksburg, VA 24061, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

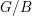We obtain an algorithm computing the Chern–Schwartz–MacPherson (CSM) classes of Schubert cells in a generalized flag manifold $G/B$ . In analogy to how the ordinary divided difference operators act on Schubert classes, each CSM class of a Schubert class is obtained by applying certain Demazure–Lusztig-type operators to the CSM class of a cell of dimension one less. These operators define a representation of the Weyl group on the homology of 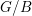$G/B$ . By functoriality, we deduce algorithmic expressions for CSM classes of Schubert cells in any flag manifold 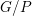$G/P$ . We conjecture that the CSM classes of Schubert cells are an effective combination of (homology) Schubert classes, and prove that this is the case in several classes of examples. We also extend our results and conjecture to the torus equivariant setting.

Keywords

Chern–Schwartz–MacPherson classhomogeneous spaceSchubert varietyDemazure–Lusztig operator

MSC classification

Primary: 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 14C17: Intersection theory, characteristic classes, intersection multiplicities 14N15: Classical problems, Schubert calculus
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 12 , December 2016 , pp. 2603 - 2625
Copyright
© The Authors 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aluffi, P., Differential forms with logarithmic poles and Chern–Schwartz–MacPherson classes of singular varieties , C. R. Acad. Sci. Paris Sér. I Math. 329 (1999), 619–624.Google Scholar
Aluffi, P., Classes de Chern des variétés singulières, revisitées , C. R. Math. Acad. Sci. Paris Sér. I Math. 342 (2006), 405–410.CrossRefGoogle Scholar
Aluffi, P., Limits of Chow groups, and a new construction of Chern–Schwartz–MacPherson classes , Pure Appl. Math. Q. 2 (2006), 915–941.CrossRefGoogle Scholar
Aluffi, P. and Mihalcea, L. C., Chern classes of Schubert cells and varieties , J. Algebraic Geom. 18 (2009), 63–100.Google Scholar
Bernšteĭn, I. N., Gel’fand, I. M. and Gel’fand, S. I., Schubert cells, and the cohomology of the spaces G/P , Uspekhi Mat. Nauk 28 (1973), 3–26.Google Scholar
Billey, S. and Lakshmibai, V., Singular loci of Schubert varieties, Progress in Mathematics, vol. 182 (Birkhäuser, Boston, MA, 2000).CrossRefGoogle Scholar
Brion, M. and Kumar, S., Frobenius splitting methods in geometry and representation theory, Progress in Mathematics, vol. 231 (Birkhäuser, Boston, MA, 2005).Google Scholar
Fulton, W., Intersection theory, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. [A Series of Modern Surveys in Mathematics], vol. 2, second edition (Springer, Berlin, 1998).Google Scholar
Fulton, W. and Woodward, C., On the quantum product of Schubert classes , J. Algebraic Geom. 13 (2004), 641–661.Google Scholar
Ginzburg, V., Characteristic varieties and vanishing cycles , Invent. Math. 84 (1986), 327–402.Google Scholar
Ginzburg, V., Geometric methods in the representation theory of Hecke algebras and quantum groups , in Representation theories and algebraic geometry (Montreal, PQ, 1997), NATO Advanced Science Institute Series C, Mathematical and Physical Sciences, vol. 514 (Kluwer Academic, Dordrecht, 1998), 127–183, notes by Vladimir Baranovsky [V. Yu. Baranovskiĭ].Google Scholar
Goresky, M. and Pardon, W., Chern classes of automorphic vector bundles , Invent. Math. 147 (2002), 561–612.Google Scholar
Huh, J., Positivity of Chern classes of Schubert cells and varieties , J. Algebraic Geom. 25 (2016), 177–199.Google Scholar
Humphreys, J. E., Reflection groups and Coxeter groups, Cambridge Studies in Advanced Mathematics, vol. 29 (Cambridge University Press, Cambridge, 1990).CrossRefGoogle Scholar
Jones, B. F., Singular Chern classes of Schubert varieties via small resolution , Int. Math. Res. Not. IMRN 2010 (2010), 1371–1416.Google Scholar
Kennedy, G., MacPherson’s Chern classes of singular algebraic varieties , Comm. Algebra 18 (1990), 2821–2839.CrossRefGoogle Scholar
Knutson, A., A Schubert calculus recurrence from the noncomplex $W$ -action on $G/B$ , Preprint (2003), arXiv:math/0306304v1.Google Scholar
MacPherson, R. D., Chern classes for singular algebraic varieties , Ann. of Math. (2) 100 (1974), 423–432.CrossRefGoogle Scholar
Maulik, D. and Okounkov, A., Quantum groups and quantum cohomology, Preprint (2012),arXiv:1211.1287.Google Scholar
Mihalcea, L. C., Binomial determinants and positivity of Chern–Schwartz–MacPherson classes , Australas. J. Combin. 62 (2015), 155–171.Google Scholar
Ohmoto, T., Equivariant Chern classes of singular algebraic varieties with group actions , Math. Proc. Cambridge Philos. Soc. 140 (2006), 115–134.Google Scholar
Rimányi, R., Tarasov, V. and Varchenko, A., Cohomology classes of conormal bundles of Schubert varieties and Yangian weight functions , Math. Z. 277 (2014), 1085–1104.CrossRefGoogle Scholar
Rimányi, R. and Varchenko, A., Equivariant Chern–Schwartz–MacPherson classes in partial flag varieties: interpolation and formulae, Preprint (2015), arXiv:1509.09315.Google Scholar
Schwartz, M.-H., Classes caractéristiques définies par une stratification d’une variété analytique complexe. I , C. R. Acad. Sci. Paris 260 (1965), 3262–3264.Google Scholar
Schwartz, M.-H., Classes caractéristiques définies par une stratification d’une variété analytique complexe. II , C. R. Acad. Sci. Paris 260 (1965), 3535–3537.Google Scholar
Stryker, J. P. III, Chern–Schwartz–MacPherson classes of graph hypersurfaces and Schubert varieties, PhD thesis, The Florida State University (2011).Google Scholar
Su, C., Restriction formula for stable basis of the Springer resolution, Selecta Math., to appear. Preprint (2015), arXiv:1501.04214.Google Scholar
Tymoczko, J. S., Permutation actions on equivariant cohomology of flag varieties , in Toric topology, Contemporary Mathematics, vol. 460 (American Mathematical Society, Providence, RI, 2008), 365–384.Google Scholar
Weber, A., Equivariant Chern classes and localization theorem , J. Singul. 5 (2012), 153–176.Google Scholar