Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-25T04:42:21.412Z Has data issue: false hasContentIssue false
  • English
  • Français

Characterization of products of theta divisors

Part of: (Co)homology theory Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  30 June 2014

Zhi Jiang ,
Martí Lahoz  and
Sofia Tirabassi
Zhi Jiang
Affiliation:
Département de Mathématiques d’Orsay, Université Paris-Sud 11, Bâtiment 425, F-91405 Orsay, France email [email protected]
Martí Lahoz
Affiliation:
Département de Mathématiques d’Orsay, Université Paris-Sud 11, Bâtiment 425, F-91405 Orsay, France email [email protected] Current address: Institut de Mathématiques de Jussieu, Université Paris 7 Denis Diderot, Bâtiment Sophie-Germain, Case 7032, F-75205 Paris, France
Sofia Tirabassi
Affiliation:
Math Department, University of Utah, 155 S 1400 E, Salt Lake City, UT 84112, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study products of irreducible theta divisors from two points of view. On the one hand, we characterize them as normal subvarieties of abelian varieties such that a desingularization has holomorphic Euler characteristic 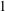$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}1$. On the other hand, we identify them up to birational equivalence among all varieties of maximal Albanese dimension. We also describe the structure of varieties 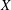$X$ of maximal Albanese dimension, with holomorphic Euler characteristic 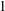$1$ and irregularity 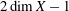$2\dim X-1$.

Keywords

theta divisorsEuler characteristicgeneric vanishing

MSC classification

Secondary: 14J10: Families, moduli, classification 14F17: Vanishing theorems 14E05: Rational and birational maps
Type
Research Article
Information
Compositio Mathematica , Volume 150 , Issue 8 , August 2014 , pp. 1384 - 1412
Copyright
© The Author(s) 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barja, M. A., Lahoz, M., Naranjo, J. C. and Pareschi, G., On the bicanonical map of irregular varieties, J. Algebraic Geom. 21 (2012), 445–471.Google Scholar
Beauville, A., Surfaces algébriques complexes, Astérisque 54 (1978).Google Scholar
Campana, F., Remarques sur le revêtement universel des variétés kählériennes compactes, Bull. Soc. Math. France 122 (1994), 255–284.Google Scholar
Chen, J. A., Debarre, O. and Jiang, Z., (2012), Varieties with vanishing holomorphic Euler characteristic, published online, J. Reine Angew. Math., doi:10.1515/crelle-2012-0073.Google Scholar
Chen, J. A. and Hacon, C. D., Pluricanonical maps of varieties of maximal Albanese dimension, Math. of Ann. (2) 320 (2001), 367–380.Google Scholar
Chen, J. A. and Hacon, C. D., A surface of general type with p g= q = 2 and K X2 = 5, Pacific J. Math. 223 (2006), 219–228.Google Scholar
Debarre, O., Inégalités numériques pour les surfaces de type général, Bull. Soc. Math. France 110 (1982), 319–346.Google Scholar
Debarre, O. and Hacon, C. D., Singularities of divisors on abelian varieties, Manuscripta Math. 122 (2007), 217–228.Google Scholar
Ein, L. and Lazarsfeld, R., Singularities of theta divisors and the birational geometry of irregular varieties, J. Amer. Math. Soc. 10 (1997), 243–258.Google Scholar
Green, M. and Lazarsfeld, R., Deformation theory, generic vanishing theorems, and some conjectures of Enriques, Catanese and Beauville, Invent. Math. 90 (1987), 389–407.Google Scholar
Green, M. and Lazarsfeld, R., Higher obstructions to deforming cohomology groups of line bundles, J. Amer. Math. Soc. 4 (1991), 87–103.Google Scholar
Hacon, C. D., Fourier transforms, generic vanishing theorems and polarizations of abelian varieties, Math. Z. 235 (2000), 717–726.CrossRefGoogle Scholar
Hacon, C. D. and Pardini, R., On the birational geometry of varieties of maximal Albanese dimension, J. Reine Angew. Math. 546 (2002), 177–199.Google Scholar
Hacon, C. D. and Pardini, R., Surfaces with p g= q = 3, Trans. Amer. Math. Soc. 354 (2002), 2631–2638.Google Scholar
Hacon, C. D. and Pardini, R., Birational characterization of products of curves of genus 2, Math. Res. Lett. 12 (2005), 129–140.Google Scholar
Huybrechts, D., Fourier–Mukai transforms in algebraic geometry, Oxford Mathematical Monographs (Clarendon Press, 2006).Google Scholar
Jiang, Z., Lahoz, M. and Tirabassi, S., On the Iitaka fibration of varieties of maximal Albanese dimension, Int. Math. Res. Not. IMRN 2013 (2013), 2984–3005.Google Scholar
Kollár, J., Higher direct images of dualizing sheaves. I, Ann. of Math. (2) 123 (1986), 11–42.Google Scholar
Kollár, J., Higher direct images of dualizing sheaves. II, Ann. of Math. (2) 124 (1986), 171–202.Google Scholar
Lazarsfeld, R. and Popa, M., Derivative complex, BGG correspondence, and numerical inequalities for compact Kähler manifolds, Invent. Math. 182 (2010), 605–633.Google Scholar
Mori, S., Classification of higher-dimensional varieties, in Algebraic geometry, Bowdoin, 1985 (Brunswick, Maine, 1985), Proceedings of Symposia in Pure Mathematics, vol. 46, Part 1 (American Mathematical Society, Providence, RI, 1987), 269–331.Google Scholar
Mukai, S., Duality between D (X) and D (X̂) with its application to Picard sheaves, Nagoya Math. J. 81 (1981), 153–175.Google Scholar
Pareschi, G., Basic results on irregular varieties via Fourier–Mukai methods, in Current developments in algebraic geometry, Mathematical Sciences Research Institute Publications, vol. 59 (Cambridge University Press, Cambridge, 2012), 379–403.Google Scholar
Pareschi, G. and Popa, M., Regularity on abelian varieties I, J. Amer. Math. Soc. 16 (2003), 285–302.Google Scholar
Pareschi, G. and Popa, M., Strong generic vanishing and a higher-dimensional Castelnuovo–de Franchis inequality, Duke Math. J. 150 (2009), 269–285.Google Scholar
Pareschi, G. and Popa, M., Regularity on abelian varieties III: relationship with generic vanishing and applications, in Grassmannians, moduli spaces and vector bundles, Clay Mathematics Proceedings, vol. 14 (American Mathematical Society, Providence, RI, 2011), 141–167.Google Scholar
Penegini, M. and Polizzi, F., Surfaces with p g= q = 2, K 2 = 6, and Albanese map of degree 2, Canad. J. Math. 65 (2013), 195–221.Google Scholar
Penegini, M. and Polizzi, F., On surfaces with p g= q = 2, K 2 = 5 and Albanese map of degree 3, Osaka J. Math. 50 (2013), 643–686.Google Scholar
Pirola, G. P., Surfaces with p g= q = 3, Manuscripta Math. 108 (2002), 163–170.Google Scholar
Serrano, F., Isotrivial fibered surfaces, Ann. Mat. Pura Appl. (IV) 171 (1996), 63–81.Google Scholar
Simpson, C., Subspaces of moduli spaces of rank one local systems, Ann. Sci. Éc. Norm. Supér. 26 (1993), 361–401.Google Scholar
Tirabassi, S., Syzygies, pluricanonical maps and the birational geometry of irregular varieties (Università degli studi Roma TRE, 2012).Google Scholar
Ueno, K., Classification theory of algebraic varieties and compact complex spaces, Lecture Notes in Mathematics, vol. 439 (Springer, 1975).Google Scholar
Viehweg, E., Positivity of direct image sheaves and applications to families of higher dimensional manifolds, ICTP Lecture Notes, vol. 6 (ICTP, Trieste, 2001), 249–284.Google Scholar
Viehweg, E., Weak positivity and the additivity of the Kodaira dimension for certain fiber spaces, in Algebraic varieties and analytic varieties (Tokyo, 1981), Advanced Studies in Pure Mathematics, vol. 1 (North-Holland, Amsterdam, 1983), 329–353.Google Scholar
Zhang, L., (2012), On the bicanonical maps of primitive varieties with $q(X) = {\rm dim}(X)$: the degree and the Euler number, Math. Z., to appear, doi:10.1007/s00209-013-1266-2.Google Scholar