Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T05:15:29.947Z Has data issue: false hasContentIssue false
  • English
  • Français

The special linear version of the projective bundle theorem

Part of: (Co)homology theory $K$-theory of forms

Published online by Cambridge University Press:  07 November 2014

Alexey Ananyevskiy
Alexey Ananyevskiy*
Affiliation:
Chebyshev Laboratory, St. Petersburg State University, 14th Line, 29b, Saint Petersburg 199178, Russia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

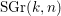A special linear Grassmann variety $\text{SGr}(k,n)$ is the complement to the zero section of the determinant of the tautological vector bundle over 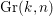$\text{Gr}(k,n)$. For an 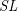$SL$-oriented representable ring cohomology theory 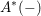$A^{\ast }(-)$ with invertible stable Hopf map 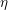${\it\eta}$, including Witt groups and 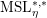$\text{MSL}_{{\it\eta}}^{\ast ,\ast }$, we have 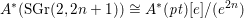$A^{\ast }(\text{SGr}(2,2n+1))\cong A^{\ast }(pt)[e]/(e^{2n})$, and 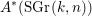$A^{\ast }(\text{SGr}(k,n))$ is a truncated polynomial algebra over 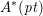$A^{\ast }(pt)$ whenever 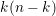$k(n-k)$ is even. A splitting principle for such theories is established. Using the computations for the special linear Grassmann varieties, we obtain a description of 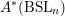$A^{\ast }(\text{BSL}_{n})$ in terms of homogeneous power series in certain characteristic classes of tautological bundles.

Keywords

special linear orientationstable Hopf mapEuler classPontryagin classesWitt groups

MSC classification

Primary: 14F42: Motivic cohomology; motivic homotopy theory 19G12: Witt groups of rings 19G99: None of the above, but in this section
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 3 , March 2015 , pp. 461 - 501
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ananyevskiy, A., On the relation of special linear algebraic cobordism to Witt groups, Preprint (2013), arXiv:1212.5780v2.Google Scholar
Conner, P. E. and Floyd, E. E., The relation of cobordism to K-theories, Lecture Notes in Mathematics, vol. 28 (Springer, Berlin, 1966).Google Scholar
Balmer, P., Derived Witt groups of a scheme, J. Pure Appl. Algebra 141 (1999), 101–129.CrossRefGoogle Scholar
Balmer, P., Witt groups, in Handbook of K-theory, Vols. 1, 2 (Springer, Berlin, 2005), 539–576.Google Scholar
Balmer, P. and Calmès, B., Witt groups of Grassmann varieties, J. Algebraic Geom. 21 (2012), 601–642.Google Scholar
Balmer, P. and Gille, S., Koszul complexes and symmetric forms over the punctured affine space, Proc. Lond. Math. Soc. (3) 91 (2005), 273–299.Google Scholar
Fulton, W., Young tableaux, with applications to representation theory and geometry (Cambridge University Press, Cambridge, 1997).Google Scholar
Hornbostel, J., A1-representability of Hermitian K-theory and Witt groups, Topology 44 (2005), 661–687.Google Scholar
Jardine, J. F., Motivic symmetric spectra, Doc. Math. 5 (2000), 445–552.CrossRefGoogle Scholar
Morel, F., An introduction to A1-homotopy theory, in Contemporary developments in algebraic K-theory, ICTP Lecture Notes, vol. XV (Abdus Salam International Center for Theoretical Physics, Trieste, 2004), 357–441.Google Scholar
Morel, F., A1-Algebraic topology over a field, Lecture Notes in Mathematics, vol. 2052 (Springer, 2012).Google Scholar
Morel, F. and Voevodsky, V., A1-homotopy theory of schemes, Publ. Math. Inst. Hautes Études Sci. 90 (1999), 45–143.CrossRefGoogle Scholar
Nenashev, A., Gysin maps in oriented theories, J. Algebra 302 (2006), 200–213.Google Scholar
Nenashev, A., Gysin maps in Balmer–Witt theory, J. Pure Appl. Algebra 211 (2007), 203–221.Google Scholar
Panin, I., Pimenov, K. and Röndigs, O., On the relation of Voevodsky’s algebraic cobordism to Quillen’s K-theory, Invent. Math. 175 (2009), 435–451.CrossRefGoogle Scholar
Panin, I., Pimenov, K. and Röndigs, O., On Voevodsky’s algebraic K-theory spectrum, in Algebraic topology, Abel Symposium, vol. 4 (Springer, Berlin, 2009), 279–330.Google Scholar
Panin, I. and Smirnov, A., Oriented cohomology theories of algebraic varieties, K-Theory 30 (2003), 265–314.CrossRefGoogle Scholar
Panin, I. and Walter, C., Quaternionic Grassmannians and Pontryagin classes in algebraic geometry, Preprint (2011), arXiv:1011.0649.Google Scholar
Panin, I. and Walter, C., On the motivic commutative spectrum BO, Preprint (2011),arXiv:1011.0650.Google Scholar
Panin, I. and Walter, C., On the algebraic cobordism spectra MSL and MSp, Preprint (2011),arXiv:1011.0651.Google Scholar
Panin, I. and Walter, C., On the relation of the symplectic algebraic cobordism to hermitian K-theory, Preprint (2011), arXiv:1011.0652.Google Scholar
Schlichting, M., Hermitian K-theory of exact categories, J. K-Theory 5 (2010), 105–165.Google Scholar
Voevodsky, V., A1-homotopy theory, Doc. Math. Extra Vol. I (1998), 579–604.Google Scholar