Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-27T19:20:33.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Schiffer variations and the generic Torelli theorem for hypersurfaces

Part of: Cycles and subschemes Families, fibrations Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  08 February 2022

Claire Voisin
Claire Voisin*
Affiliation:
CNRS, IMJ-PRG, 4 Place Jussieu, 75005 Paris, France [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove the generic Torelli theorem for hypersurfaces in 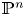$\mathbb {P}^{n}$ of degree 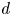$d$ dividing 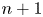$n+1$, for 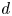$d$ sufficiently large. Our proof involves the higher-order study of the variation of Hodge structure along particular one-parameter families of hypersurfaces that we call ‘Schiffer variations.’ We also analyze the case of degree 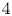$4$. Combined with Donagi's generic Torelli theorem and results of Cox and Green, this shows that the generic Torelli theorem for hypersurfaces holds with finitely many exceptions.

Keywords

Hodge structuresvariation of Hodge structurehypersurfacesTorelli theorem

MSC classification

Primary: 14C30: Transcendental methods, Hodge theory , Hodge conjecture 14C34: Torelli problem 14D07: Variation of Hodge structures 14J70: Hypersurfaces
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 1 , January 2022 , pp. 89 - 122
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The author is supported by the ERC Synergy Grant HyperK (Grant agreement No. 854361).

References

Bardelli, F. and Pirola, G., Curves of genus $g$ lying on a $g$-dimensional Jacobian variety, Invent. Math. 95 (1989), 263–276.CrossRefGoogle Scholar
Beauville, A., Les singularités du diviseur Theta de la jacobienne intermédiaire de l'hypersurface cubique dans $\mathbb {P}^{4}$, in Algebraic threefolds, Varenna, 1981, Lecture Notes in Mathematics, vol. 947 (Springer, 1982), 190–208.10.1007/BFb0093588CrossRefGoogle Scholar
Bogomolov, F. A., Holomorphic tensors and vector bundles on projective manifolds, Izv. Akad. Nauk SSSR Ser. Mat. 42 (1978), 1227–1287.Google Scholar
Carlson, J. and Griffiths, P., Infinitesimal variations of Hodge structure and the global Torelli theorem, in Géométrie algébrique, Angers, 1979, ed. Beauville, A. (Sijthoff-Noordhoff, 1980), 51–76.Google Scholar
Cattani, E., Deligne, P. and Kaplan, A., On the locus of Hodge classes, J. Amer. Math. Soc. 8 (1995), 483–506.10.1090/S0894-0347-1995-1273413-2CrossRefGoogle Scholar
Clemens, C. H. and Griffiths, P., The intermediate Jacobian of the cubic threefold, Ann. of Math. (2) 95 (1972), 281–356.10.2307/1970801CrossRefGoogle Scholar
Cox, D. and Green, M., Polynomial structures and generic Torelli for projective hypersurfaces, Compos. Math. 73 (1990), 121–124.Google Scholar
Donagi, R., Generic Torelli for projective hypersurfaces, Compos. Math. 50 (1983), 325–353.Google Scholar
Donagi, R. and Green, M., A new proof of the symmetrizer lemma and a stronger weak Torelli theorem for projective hypersurfaces, J. Differential Geom. 20 (1984), 459–461.CrossRefGoogle Scholar
Griffiths, P., On the periods of certain rational integrals, I and II, Ann. of Math. (2) 90 (1969), 460–541.CrossRefGoogle Scholar
Huybrechts, D. and Rennemo, J., Hochschild cohomology versus the Jacobian ring and the Torelli theorem for cubic fourfolds, Algebr. Geom. 6 (2019), 76–99.CrossRefGoogle Scholar
Mather, J. and Yau, S., Classification of isolated hypersurface singularities by their moduli algebras, Invent. Math. 69 (1982), 243–251.CrossRefGoogle Scholar
Piateski-Shapiro, A. and Shafarevich, I., Torelli's theorem for algebraic surfaces of type K3, Izv. Akad. Nauk SSSR Ser. Mat. 35 (1971), 530–572.Google Scholar
Tsuji, H., Stability of tangent bundles of minimal algebraic varieties, Topology 27 (1988), 429–442.CrossRefGoogle Scholar
Voisin, C., Théorème de Torelli pour les cubiques de $\mathbb {P}^{5}$, Invent. Math. 86 (1986), 577–601 (erratum Invent. Math. 172 (2008), 455–45).CrossRefGoogle Scholar
Voisin, C., A generic Torelli theorem for the quintic threefold, in New trends in algebraic geometry, eds Hulek, K., Catanese, F., Peters, Ch. and Reid, M., London Mathematical Society Lecture Note Series, vol. 264 (Cambridge University Press, 1999).Google Scholar
Voisin, C., Hodge theory and complex algebraic geometry II (Cambridge University Press, 2003).CrossRefGoogle Scholar
Yau, S.-T., On the Ricci curvature of a compact Kähler manifold and the complex Monge-Ampère equation. I, Comm. Pure Appl. Math. 31 (1978), 339–411.10.1002/cpa.3160310304CrossRefGoogle Scholar