Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Schneider, Friedrich Martin
2019.
Equivariant dissipation in non-archimedean groups.
Israel Journal of Mathematics,
Vol. 234,
Issue. 1,
p.
281.
Schneider, Friedrich Martin
2019.
Equivariant concentration in topological groups.
Geometry & Topology,
Vol. 23,
Issue. 2,
p.
925.
Schneider, Friedrich Martin
and
Solecki, Sławomir
2021.
Concentration of measure, classification of submeasures, and dynamics of L0.
Journal of Functional Analysis,
Vol. 280,
Issue. 5,
p.
108890.
Bühler, Theo
and
Kaimanovich, Vadim
2021.
Topology, Geometry, and Dynamics.
Vol. 772,
Issue. ,
p.
69.
Ivanov, Aleksander
2021.
Metric groups, unitary representations and continuous logic.
Communications in Mathematics,
Vol. 29,
Issue. 1,
p.
35.
Duda, Karol
and
Ivanov (Iwanow), Aleksander
2022.
Computable paradoxical decompositions.
International Journal of Algebra and Computation,
Vol. 32,
Issue. 05,
p.
953.
HAUSER, TILL
and
SCHNEIDER, FRIEDRICH MARTIN
2024.
Entropy of group actions beyond uniform lattices.
Ergodic Theory and Dynamical Systems,
p.
1.
Pestov, Vladimir G.
and
Schneider, Friedrich Martin
2024.
On invariant means and pre-syndetic subgroups.
Topology and its Applications,
p.
109093.
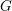 $G$
is amenable if and only if its left-translation action can be approximated in a uniform manner by amenable actions on the set
$G$
is amenable if and only if its left-translation action can be approximated in a uniform manner by amenable actions on the set
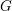 $G$
. As applications we obtain a topological version of Whyte’s geometric solution to the von Neumann problem and give an affirmative answer to a question posed by Rosendal.
$G$
. As applications we obtain a topological version of Whyte’s geometric solution to the von Neumann problem and give an affirmative answer to a question posed by Rosendal.