Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cho, Peter J.
and
Kim, Henry H.
2013.
Probabilistic properties of number fields.
Journal of Number Theory,
Vol. 133,
Issue. 12,
p.
4175.
Lamzouri, Youness
2015.
The distribution of Euler–Kronecker constants of quadratic fields.
Journal of Mathematical Analysis and Applications,
Vol. 432,
Issue. 2,
p.
632.
Cho, Peter J.
and
Kim, Henry H.
2018.
Moments of logarithmic derivatives of L-functions.
Journal of Number Theory,
Vol. 183,
Issue. ,
p.
40.
Cho, Peter J
and
Kim, Henry H
2020.
The Average of the Smallest Prime in a Conjugacy Class.
International Mathematics Research Notices,
Vol. 2020,
Issue. 6,
p.
1718.
Kim, Henry H.
2021.
Extreme Values of Euler-Kronecker Constants.
Uniform distribution theory,
Vol. 16,
Issue. 1,
p.
41.
Kim, Henry H.
2021.
Minimal generators of the ideal class group.
Journal of Number Theory,
Vol. 222,
Issue. ,
p.
157.
Garcia, Stephan Ramon
and
Lee, Ethan Simpson
2022.
Explicit estimates for Artin L-functions: Duke's short-sum theorem and Dedekind zeta residues.
Journal of Number Theory,
Vol. 238,
Issue. ,
p.
920.
Paul, Biplab
2023.
On values of logarithmic derivative of L-function attached to modular form.
International Journal of Number Theory,
Vol. 19,
Issue. 03,
p.
531.
Kim, Henry H.
2023.
Fourier coefficients of automorphic L-functions.
International Journal of Number Theory,
Vol. 19,
Issue. 10,
p.
2513.
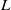 $L$-functions
$L$-functions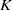 $K$ be a number field of degree
$K$ be a number field of degree  $n$, and let
$n$, and let 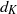 $d_K$ be its discriminant. Then, under the Artin conjecture, the generalized Riemann hypothesis and a certain zero-density hypothesis, we show that the upper and lower bounds of the logarithmic derivatives of Artin
$d_K$ be its discriminant. Then, under the Artin conjecture, the generalized Riemann hypothesis and a certain zero-density hypothesis, we show that the upper and lower bounds of the logarithmic derivatives of Artin 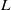 $L$-functions attached to
$L$-functions attached to 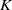 $K$ at
$K$ at 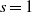 $s=1$ are
$s=1$ are 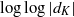 $\log \log |d_K|$ and
$\log \log |d_K|$ and 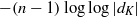 $-(n-1) \log \log |d_K|$, respectively. Unconditionally, we show that there are infinitely many number fields with the extreme logarithmic derivatives; they are families of number fields whose Galois closures have the Galois group
$-(n-1) \log \log |d_K|$, respectively. Unconditionally, we show that there are infinitely many number fields with the extreme logarithmic derivatives; they are families of number fields whose Galois closures have the Galois group 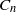 $C_n$ for
$C_n$ for 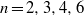 $n=2,3,4,6$,
$n=2,3,4,6$, 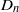 $D_n$ for
$D_n$ for 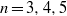 $n=3,4,5$,
$n=3,4,5$, 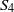 $S_4$ or
$S_4$ or 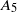 $A_5$.
$A_5$.