Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-21T17:49:43.481Z Has data issue: false hasContentIssue false
  • English
  • Français

Constructing elliptic curves from Galois representations

Part of: Arithmetic algebraic geometry Abelian varieties and schemes

Published online by Cambridge University Press:  29 August 2018

Andrew Snowden  and
Jacob Tsimerman
Andrew Snowden
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI, USA email [email protected]://www-personal.umich.edu/∼asnowden/
Jacob Tsimerman
Affiliation:
Department of Mathematics, University of Toronto, Toronto, CA, Canada email [email protected]://www.math.toronto.edu/∼jacobt/
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a non-isotrivial elliptic curve over an arithmetic surface, one obtains a lisse 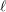$\ell$-adic sheaf of rank two over the surface. This lisse sheaf has a number of straightforward properties: cyclotomic determinant, finite ramification, rational traces of Frobenius elements, and somewhere not potentially good reduction. We prove that any lisse sheaf of rank two possessing these properties comes from an elliptic curve.

Keywords

Fontaine–Mazur conjectureDrinfeld modular curveLanglands program

MSC classification

Primary: 11G05: Elliptic curves over global fields 14K15: Arithmetic ground fields
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 10 , October 2018 , pp. 2045 - 2054
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

AS was supported by NSF grants DMS-1303082 and DMS-1453893 and a Sloan Fellowship.

References

Bosch, S., Lütkebohmert, W. and Raynaud, M., Néron models (Springer, Berlin, 1990).Google Scholar
Drinfeld, V. G., Elliptic modules II , Math. USSR-Sb 31 (1977), 159–170.Google Scholar
Drinfeld, V. G., Langland’s conjecture for GL(2) over function fields , in Proc. Int. Congress Mathematicians, Helsinki, 1978 (Academia Scientiarum Fennica, 1980), 565–574.Google Scholar
Drinfed, V. G., Two-dimensional ℓ-adic representations of the fundamental group of a curve over a finite field and automorphic forms on GL(2) , Amer. J. Math. 105 (1983), 85–114.Google Scholar
Faltings, G., Wüstholz, G., Grunewald, F., Schappacher, N. and Stuhler, U., Rational points, Aspects of Mathematics, vol. E6, third edition (Vieweg, Braunschweig, 1992).Google Scholar
Milne, J. S., Abelian varieties, http://www.jmilne.org/math/CourseNotes/AV110.pdf.Google Scholar
Serre, J.-P., Zeta and L functions , in Arithmetical algebraic geometry (Harper and Row, New York, NY, 1965), 82–92.Google Scholar
Grothendieck, A. and Raynaud, M., Revêtements étales et groupe fondamental (SGA 1), Documents Mathématiques (Paris), vol. 3 (Société Mathématique de France, 2003).Google Scholar
Shimura, G., Algebraic number fields and symplectic discontinuous groups , Ann. of Math. (2) 86 (1967), 503–592.Google Scholar
Taylor, R., Remarks on a conjecture of Fontaine and Mazur , J. Inst. Math. Jussieu 1 (2002), 125–143.Google Scholar