Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T01:28:31.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Characteristic directions of two-dimensional biholomorphisms

Part of: Holomorphic mappings and correspondences Singularities Complex dynamical systems

Published online by Cambridge University Press:  31 March 2020

Lorena López-Hernanz  and
Rudy Rosas
Lorena López-Hernanz
Affiliation:
Departamento de Física y Matemáticas, Universidad de Alcalá, Edificio de Ciencias, Carretera Madrid-Barcelona, Km. 33600, 28871Alcalá de Henares, Madrid, Spain email [email protected]
Rudy Rosas
Affiliation:
Departamento de Ciencias, Pontificia Universidad Católica del Perú, Av. Universitaria 1801, Lima, Peru email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for each characteristic direction 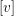$[v]$ of a tangent to the identity diffeomorphism of order 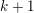$k+1$ in 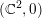$(\mathbb{C}^{2},0)$ there exist either an analytic curve of fixed points tangent to 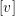$[v]$ or 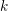$k$ parabolic manifolds where all the orbits are tangent to 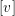$[v]$, and that at least one of these parabolic manifolds is or contains a parabolic curve.

Keywords

local holomorphic dynamicstangent to the identity mapscharacteristic directionsparabolic manifolds

MSC classification

Primary: 32H50: Iteration problems 37F99: None of the above, but in this section 32S65: Singularities of holomorphic vector fields and foliations
Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 5 , May 2020 , pp. 869 - 880
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author was partially supported by Ministerio de Economía y Competitividad, Spain, process MTM2016-77642-C2-1-P; the second author was supported by Vicerrectorado de Investigación de la Pontificia Universidad Católica del Perú.

References

Abate, M., The residual index and the dynamics of holomorphic maps tangent to the identity, Duke Math. J. 107 (2001), 173–207.CrossRefGoogle Scholar
Abate, M., Fatou flowers and parabolic curves, in Complex analysis and geometry, Springer Proceedings in Mathematics and Statistics, vol. 144 (Springer, Tokyo, 2015), 1–39.Google Scholar
Astorg, M., Buff, X., Dujardin, R., Peters, H. and Raissy, J., A two-dimensional polynomial mapping with a wandering Fatou component, Ann. of Math. (2) 184 (2016), 263–313.CrossRefGoogle Scholar
Brochero, F. E., Cano, F. and López-Hernanz, L., Parabolic curves for diffeomorphisms in ℂ2, Publ. Mat. 52 (2008), 189–194.CrossRefGoogle Scholar
Brunella, M., Some remarks on indices of holomorphic vector fields, Publ. Mat. 41 (1997), 527–544.CrossRefGoogle Scholar
Camacho, C., Lins Neto, A. and Sad, P., Topological invariants and equidesingularization for holomorphic vector fields, J. Differential Geom. 20 (1984), 143–174.CrossRefGoogle Scholar
Camacho, C. and Sad, P., Invariant varieties through singularities of holomorphic vector fields, Ann. of Math. (2) 115 (1982), 579–595.CrossRefGoogle Scholar
Camacho, C. and Sad, P., Pontos singulares de equações diferenciais analíticas, in 16° Colóquio Brasileiro de Matemática (Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, 1987).Google Scholar
Cano, F., Cerveau, D. and Déserti, J., Théorie élémentaire des feuilletages holomorphes singuliers, Échelles (Éditions Belin, Paris, 2013).Google Scholar
Écalle, J., Les fonctions résurgentes. Tome III. L’équation du pont et la classification analytique des objects locaux, Publications Mathématiques d’Orsay, 85-5 (Université de Paris-Sud, Département de Mathématiques, Orsay, 1985).Google Scholar
Fatou, P., Sur les équations fonctionelles, Bull. Soc. Math. France 47 (1919), 161–271.CrossRefGoogle Scholar
Hakim, M., Analytic transformations of (ℂp, 0) tangent to the identity, Duke Math. J. 92 (1998), 403–428.CrossRefGoogle Scholar
Leau, L., Étude sur les équations fonctionelles à une ou à plusieurs variables, Ann. Fac. Sci. Toulouse Sci. Math. Sci. Phys. 11 (1897), 1–110.Google Scholar
López-Hernanz, L., Raissy, J., Ribón, J. and Sanz-Sánchez, F., Stable manifolds of two-dimensional biholomorphisms asymptotic to formal curves, Int. Math. Res. Not. IMRN, doi:10.1093/imrn/rnz143.Google Scholar
López-Hernanz, L. and Sanz Sánchez, F., Parabolic curves of diffeomorphisms asymptotic to formal invariant curves, J. Reine Angew. Math. 739 (2018), 277–296.CrossRefGoogle Scholar
Mattei, J. F. and Salem, E., Modules formels locaux de feuilletages holomorphes, Preprint (2004), arXiv:math/0402256.Google Scholar
Molino, L., The dynamics of maps tangent to the identity and with nonvanishing index, Trans. Amer. Math. Soc. 361 (2009), 1597–1623.CrossRefGoogle Scholar
Ribón, J., Families of diffeomorphisms without periodic curves, Michigan Math. J. 53 (2005), 243–256.CrossRefGoogle Scholar
Seidenberg, A., Reduction of the singularities of the differential equation Ady = Bdx, Amer. J. Math. 90 (1968), 248–269.CrossRefGoogle Scholar
Vivas, L., Degenerate characteristic directions for maps tangent to the identity, Indiana Univ. Math. J. 61 (2012), 2019–2040.CrossRefGoogle Scholar