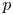Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T02:10:46.197Z Has data issue: false hasContentIssue false
  • English
  • Français

Big principal series, $p$-adic families and 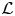$\mathcal {L}$-invariants

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  25 April 2022

Lennart Gehrmann  and
Giovanni Rosso
Lennart Gehrmann
Affiliation:
Fakultät für Mathematik, Universität Duisburg-Essen, Thea-Leymann-Straße 9, 45127 Essen, [email protected]
Giovanni Rosso
Affiliation:
Departments of Mathematics and Statistics, Concordia University, 1455 De Maisonneuve Blvd. W., Montréal, Québec, Canada H3G 1M8 [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In earlier work, the first named author generalized the construction of Darmon-style 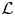$\mathcal {L}$-invariants to cuspidal automorphic representations of semisimple groups of higher rank, which are cohomological with respect to the trivial coefficient system and Steinberg at a fixed prime. In this paper, assuming that the Archimedean component of the group has discrete series we show that these automorphic 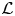$\mathcal {L}$-invariants can be computed in terms of derivatives of Hecke eigenvalues in 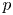$p$-adic families. Our proof is novel even in the case of modular forms, which was established by Bertolini, Darmon and Iovita. The main new technical ingredient is the Koszul resolution of locally analytic principal series representations by Kohlhaase and Schraen. As an application of our results we settle a conjecture of Spieß: we show that automorphic 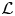$\mathcal {L}$-invariants of Hilbert modular forms of parallel weight 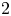$2$ are independent of the sign character used to define them. Moreover, we show that they are invariant under Jacquet–Langlands transfer and, in fact, equal to the Fontaine–Mazur 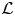$\mathcal {L}$-invariant of the associated Galois representation. Under mild assumptions, we also prove the equality of automorphic and Fontaine–Mazur 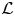$\mathcal {L}$-invariants for representations of definite unitary groups of arbitrary rank. Finally, we study the case of Bianchi modular forms to show how our methods, given precise results on eigenvarieties, can also work in the absence of discrete series representations.

Keywords

automorphic formsGalois representationsL-invariantsp-adic families

MSC classification

Primary: 11F55: Other groups and their modular and automorphic forms (several variables)
Secondary: 11F33: Congruences for modular and $p$-adic modular forms 11F70: Representation-theoretic methods; automorphic representations over local and global fields 11F75: Cohomology of arithmetic groups 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 2 , February 2022 , pp. 409 - 436
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

While working on this paper the first named author was visiting McGill University, supported by Deutsche Forschungsgemeinschaft, and he would like to thank these institutions. The second named author was partly funded by FRQNT grant 2019-NC-254031 and NSERC grant RGPIN-2018-04392. In addition, the authors would like to thank Henri Darmon, Michael Lipnowski, Vytautas Pas̆kūnas and Chris Williams for several intense and stimulating discussions. We also thank the referee for their careful reading of the paper and many suggestions.

References

Ash, A. and Stevens, G., $p$-adic deformations of arithmetic cohomology, Preprint (2008), https://math.bu.edu/people/ghs/preprints/Ash-Stevens-02-08.pdf.Google Scholar
Barnet-Lamb, T., Gee, T., Geraghty, D. and Taylor, R., Potential automorphy and change of weight, Ann. of Math. (2) 179 (2014), 501–609.CrossRefGoogle Scholar
Barrera Salazar, D., Dimitrov, M. and Jorza, A., $p$-adic $L$-functions of Hilbert cusp forms and the trivial zero conjecture, J. Eur. Math. Soc. (2021), doi:10.4171/JEMS/1165.Google Scholar
Barrera Salazar, D. and Williams, C., Exceptional zeros and $\mathcal {L}$-invariants of Bianchi modular forms, Trans. Amer. Math. Soc. 372 (2019), 1–34.CrossRefGoogle Scholar
Barrera Salazar, D. and Williams, C., Families of Bianchi modular symbols: critical base-change $p$-adic $L$-functions and $p$-adic Artin formalism, Selecta Math. (N.S.) 27 (2021), 82.CrossRefGoogle Scholar
Benois, D., $p$-adic heights and $p$-adic Hodge theory, Mém. Soc. Math. Fr. (N.S.) 167 (2021).Google Scholar
Bertolini, M., Darmon, H. and Iovita, A., Families of automorphic forms on definite quaternion algebras and Teitelbaum's conjecture, Astérisque 331 (2010), 29–64.Google Scholar
Borel, A., Admissible representations of a semi-simple group over a local field with vector fixed under an Iwahori subgroup, Invent. Math. 35 (1976), 233–260.CrossRefGoogle Scholar
Borel, A. and Serre, J.-P., Cohomologie d'immeubles et de groupes S-arithmétiques, Topology 15 (1976), 211–232.CrossRefGoogle Scholar
Caraiani, A., Monodromy and local-global compatibility for $l=p$, Algebra Number Theory 8 (2014), 1597–1646.CrossRefGoogle Scholar
Cartier, P., Representations of p-adic groups: a survey, in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 111–155.Google Scholar
Chenevier, G., The p-adic analytic space of pseudocharacters of a profinite group and pseudorepresentations over arbitrary rings, in Automorphic forms and Galois representations. Vol. 1, London Mathematical Society Lecture Note Series, vol. 414 (Cambridge University Press, Cambridge, 2014), 221–285.CrossRefGoogle Scholar
Darmon, H., Integration on $H_{ p}\times H$ and arithmetic applications, Ann. of Math. (2) 154 (2001), 589–639.CrossRefGoogle Scholar
Dasgupta, S., Stark–Heegner points on modular jacobians, Ann. Sci. Éc. Norm. Supér (4) 38 (2005), 427–469.CrossRefGoogle Scholar
Dasgupta, S. and Greenberg, M., L-invariants and Shimura curves, Algebra Number Theory 6 (2012), 455–485.CrossRefGoogle Scholar
Ding, Y., Simple $\mathcal {L}$-invariants for $\mathrm {GL}_n$, Trans. Amer. Math. Soc. 372 (2019), 7993–8042.CrossRefGoogle Scholar
Gehrmann, L., Derived Hecke algebra and automorphic L-invariants, Trans. Amer. Math. Soc. 372 (2019), 7767–7784.CrossRefGoogle Scholar
Gehrmann, L., Functoriality of automorphic $L$-invariants and applications, Doc. Math. 24 (2019), 1225–1243.Google Scholar
Gehrmann, L., Automorphic $\mathcal {L}$-invariants for reductive groups, J. Reine Angew. Math. 779 (2021), 57–103.CrossRefGoogle Scholar
Geraghty, D., Modularity lifting theorems for ordinary Galois representations, Math. Ann. 373 (2019), 1341–1427.CrossRefGoogle Scholar
Goldring, W., Galois representations associated to holomorphic limits of discrete series, Compos. Math. 150 (2014), 191–228.CrossRefGoogle Scholar
Greenberg, M., Stark–Heegner points and the cohomology of quaternionic Shimura varieties, Duke Math. J. 147 (2009), 541–575.CrossRefGoogle Scholar
Guitart, X., Masdeu, M. and Sengün, M. H., Darmon points on elliptic curves over number fields of arbitrary signature, Proc. Lond. Math. Soc. (3) 111 (2015), 484–518.CrossRefGoogle Scholar
Hansen, D., Universal eigenvarieties, trianguline Galois representations, and $p$-adic Langlands functoriality, J. Reine Angew. Math. 730 (2017), 1–64, with an appendix by James Newton.CrossRefGoogle Scholar
Howe, R. and Piatetski-Shapiro, I. I., Some examples of automorphic forms on ${\rm Sp}_{4}$, Duke Math. J. 50 (1983), 55–106.CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic forms. II, Amer. J. Math. 103 (1981), 777–815.CrossRefGoogle Scholar
Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I, Amer. J. Math. 103 (1981), 499–558.CrossRefGoogle Scholar
Januszewski, F., Rational structures on automorphic representations, Math. Ann. 370 (2018), 1805–1881.CrossRefGoogle Scholar
Knapp, A. W., Representation theory of semisimple groups, Princeton Landmarks in Mathematics (Princeton University Press, Princeton, NJ, 2001). An overview based on examples, reprint of the 1986 original.Google Scholar
Kohlhaase, J., The cohomology of locally analytic representations, J. Reine Angew. Math. 651 (2011), 187–240.Google Scholar
Kohlhaase, J. and Schraen, B., Homological vanishing theorems for locally analytic representations, Math. Ann. 353 (2012), 219–258.CrossRefGoogle Scholar
Longo, M., Rotger, V. and Vigni, S., On rigid analytic uniformization of Jacobians of Shimura curves, Amer. J. Math. 134 (2012), 1197–1246.CrossRefGoogle Scholar
Ollivier, R., Resolutions for principal series representations of $p$-adic ${\rm GL}_n$, Münster J. Math. 7 (2014), 225–240.Google Scholar
Orlik, S., On extensions of generalized Steinberg representations, J. Algebra 293 (2005), 611–630.CrossRefGoogle Scholar
Orton, L., An elementary proof of a weak exceptional zero conjecture, Can. J. Math. 56 (2004), 373–405.CrossRefGoogle Scholar
Piatetski-Shapiro, I. I., Multiplicity one theorems, in Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proceedings of Symposia in Pure Mathematics, vol. XXXIII (American Mathematical Society, Providence, RI, 1979), 209–212.Google Scholar
Reeder, M., On certain Iwahori invariants in the unramified principal series, Pacific J. Math. 153 (1992), 313–342.CrossRefGoogle Scholar
Rosso, G., $\mathcal {L}$-invariant for Siegel-Hilbert forms, Doc. Math. 20 (2015), 1227–1253.Google Scholar
Saito, T., Hilbert modular forms and $p$-adic Hodge theory, Compos. Math. 145 (2009), 1081–1113.CrossRefGoogle Scholar
Scholze, P., On torsion in the cohomology of locally symmetric varieties, Ann. of Math. (2) 182 (2015), 945–1066.10.4007/annals.2015.182.3.3CrossRefGoogle Scholar
Seveso, M. A., The Teitelbaum conjecture in the indefinite setting, Amer. J. Math. 135 (2013), 1525–1557.CrossRefGoogle Scholar
Soudry, D., A uniqueness theorem for representations of ${\rm GSO}(6)$ and the strong multiplicity one theorem for generic representations of ${\rm GSp}(4)$, Israel J. Math. 58 (1987), 257–287.CrossRefGoogle Scholar
Spieß, M., On special zeros of $p$-adic $L$-functions of Hilbert modular forms, Invent. Math. 196 (2014), 69–138.CrossRefGoogle Scholar
Spieß, M., On $\mathcal {L}$-invariants associated to Hilbert modular forms, Preprint (2020), arXiv:2005.11892.Google Scholar
Taylor, R., On Galois representations associated to Hilbert modular forms, Invent. Math. 98 (1989), 265–280.CrossRefGoogle Scholar
Teitelbaum, J. T., Values of $p$-adic $L$-functions and a $p$-adic Poisson kernel, Invent. Math. 101 (1990), 395–410.CrossRefGoogle Scholar
Thorne, J. A., Automorphy lifting for residually reducible $l$-adic Galois representations, J. Amer. Math. Soc. 28 (2015), 785–870.CrossRefGoogle Scholar
Urban, E., Eigenvarieties for reductive groups, Ann. of Math. (2) 174 (2011), 1685–1784.CrossRefGoogle Scholar
Venkat, G. and Williams, C., Stark–Heegner cycles attached to Bianchi modular forms, J. Lond. Math. Soc. 104 (2021), 394–422.CrossRefGoogle Scholar
Vignéras, M.-F., A criterion for integral structures and coefficient systems on the tree of ${\rm PGL}(2, F)$, Pure Appl. Math. Q. 4 (2008), 1291–1316.CrossRefGoogle Scholar
Wiles, A., On ordinary $\lambda$-adic representations associated to modular forms, Invent. Math. 94 (1988), 529–573.CrossRefGoogle Scholar