Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T05:03:39.541Z Has data issue: false hasContentIssue false
  • English
  • Français

Big Galois representations and 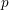$p$-adic 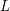$L$-functions

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  13 November 2014

Haruzo Hida
Haruzo Hida*
Affiliation:
Department of Mathematics, UCLA, Los Angeles, CA 90095-1555, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 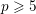$p\geqslant 5$ be a prime. If an irreducible component of the spectrum of the ‘big’ ordinary Hecke algebra does not have complex multiplication, under mild assumptions, we prove that the image of its Galois representation contains, up to finite error, a principal congruence subgroup 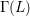${\rm\Gamma}(L)$ of 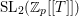$\text{SL}_{2}(\mathbb{Z}_{p}[[T]])$ for a principal ideal 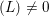$(L)\neq 0$ of 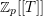$\mathbb{Z}_{p}[[T]]$ for the canonical ‘weight’ variable 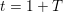$t=1+T$. If 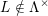$L\notin {\rm\Lambda}^{\times }$, the power series 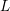$L$ is proven to be a factor of the Kubota–Leopoldt 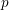$p$-adic 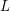$L$-function or of the square of the anticyclotomic Katz 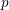$p$-adic 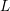$L$-function or a power of 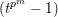$(t^{p^{m}}-1)$.

Keywords

p-adic L-functionHecke algebraGalois representationGalois deformation

MSC classification

Primary: 11F11: Holomorphic modular forms of integral weight 11F25: Hecke-Petersson operators, differential operators (one variable) 11F33: Congruences for modular and $p$-adic modular forms 11F80: Galois representations
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 4 , April 2015 , pp. 603 - 664
Copyright
© The Author 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bourbaki, N., Algèbre commutative (Hermann, Paris, 1961–1998).Google Scholar
Brown, K. S., Cohomology of groups, Graduate Texts in Mathematics, vol. 87 (Springer, New York, 1982).CrossRefGoogle Scholar
Carayol, H., Sur les représentations ℓ-adiques associées aux formes modulaires de Hilbert, Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 409–468.Google Scholar
Carayol, H., Formes modulaires et représentations galoisiennes à valeurs dans un anneau local compact, Contemp. Math. 165 (1994), 213–237.Google Scholar
Fischman, A., On the image of Λ-adic Galois representations, Ann. Inst. Fourier (Grenoble) 52 (2002), 351–378.CrossRefGoogle Scholar
Gelbart, S. S., Automorphic forms on adele groups, Annals of Mathematics Studies, vol. 83 (Princeton University Press, Princeton, NJ, 1975).Google Scholar
Ghate, E. and Vatsal, V., On the local behaviour of ordinary I-adic representations, Ann. Inst. Fourier (Grenoble) 54 (2004), 2143–2162.CrossRefGoogle Scholar
Hida, H., Iwasawa modules attached to congruences of cusp forms, Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 231–273.Google Scholar
Hida, H., Galois representations into GL2(ℤp[[X]]) attached to ordinary cusp forms, Invent. Math. 85 (1986), 545–613.CrossRefGoogle Scholar
Hida, H., Hecke algebras for GL1 and GL2, Sém. de Théorie des Nombres, Paris 1984–85, Progr. Math. 63 (1986), 131–163.Google Scholar
Hida, H., Modules of congruence of Hecke algebras and L-functions associated with cusp forms, Amer. J. Math. 110 (1988), 323–382.Google Scholar
Hida, H., Elementary theory of L-functions and Eisenstein series, London Mathematical Society Student Texts, vol. 26 (Cambridge University Press, Cambridge, 1993).Google Scholar
Hida, H., Modular forms and galois cohomology, Cambridge Studies in Advanced Mathematics, vol. 69 (Cambridge University Press, Cambridge, 2000).Google Scholar
Hida, H., Quadratic exercises in Iwasawa theory, Int. Math. Res. Notices IMRN 2009 (2009), 912–952; doi:10.1093/imrn/rnn151.Google Scholar
Hida, H., The Iwasawa 𝜇-invariant of p-adic Hecke L-functions, Ann. of Math. (2) 172 (2010), 41–137.Google Scholar
Hida, H., Geometric modular forms and elliptic curves, second edition (World Scientific Publishing Co., Singapore, 2011).CrossRefGoogle Scholar
Hida, H., Hecke fields of analytic families of modular forms, J. Amer. Math. Soc. 24 (2011), 51–80.Google Scholar
Hida, H., Constancy of adjoint L-invariant, J. Number Theory 131 (2011), 1331–1346.Google Scholar
Hida, H., Image of Λ-adic Galois representations modulo p, Invent. Math. 194 (2013), 1–40.Google Scholar
Hida, H., Local indecomposability of Tate modules of non-CM abelian varieties with real multiplication, J. Amer. Math. Soc. 26 (2013), 853–877.Google Scholar
Hida, H. and Tilouine, J., Anticyclotomic Katz p-adic L-functions and congruence modules, Ann. Sci. Éc. Norm. Supér. (4) 26 (1993), 189–259.Google Scholar
Hida, H. and Tilouine, J., On the anticyclotomic main conjecture for CM fields, Invent. Math. 117 (1994), 89–147.Google Scholar
Katz, N. M., p-adic L-functions for CM fields, Invent. Math. 49 (1978), 199–297.Google Scholar
Kutzko, P., The Langlands conjecture for Gl 2 of a local field, Ann. of Math. (2) 112 (1980), 381–412.CrossRefGoogle Scholar
Lipman, J., Desingularization of two-dimensional schemes, Ann. of Math. (2) 107 (1978), 151–207.CrossRefGoogle Scholar
Matsumura, H., Commutative ring theory, Cambridge Studies in Advanced Mathematics, vol. 8 (Cambridge University Press, New York, 1986).Google Scholar
Mazur, B., Deforming Galois representations, in Galois group over ℚ, Mathematical Sciences Research Institute Publications 16 (Springer, Berlin, 1989), 385–437.CrossRefGoogle Scholar
Mazur, B. and Tilouine, J., Représentations galoisiennes, différentielles de Kähler et ‘conjectures principales’, Publ. Math. Inst. Hautes Études Sci. 71 (1990), 65–103.Google Scholar
Mazur, B. and Wiles, A., On p-adic analytic families of Galois representations, Compositio Math. 59 (1986), 231–264.Google Scholar
Miyake, T., Modular forms, Springer Monographs in Mathematics (Springer, 1989).Google Scholar
Momose, F., On the l-adic representations attached to modular forms, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 28 (1981), 89–109.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves, Compositio Math. 115 (1999), 241–301.Google Scholar
Ohta, M., Ordinary p-adic étale cohomology groups attached to towers of elliptic modular curves. II, Math. Ann. 318 (2000), 557–583.Google Scholar
Ohta, M., Congruence modules related to Eisenstein series, Ann. Sci. Éc. Norm. Supér. (4) 36 (2003), 225–269.Google Scholar
Pink, R., Classification of pro-p subgroups of SL2 over a p-adic ring, where p is an odd prime, Compositio Math. 88 (1993), 251–264.Google Scholar
Ribet, K. A., On l-adic representations attached to modular forms, Invent. Math. 28 (1975), 245–275.Google Scholar
Ribet, K. A., A modular construction of unramified p-extensions of ℚ(𝜇p), Invent. Math. 34 (1976), 151–162.CrossRefGoogle Scholar
Ribet, K. A., On l-adic representations attached to modular forms. II, Glasg. Math. J. 27 (1985), 185–194.Google Scholar
Rubin, K., On the main conjecture of Iwasawa theory for imaginary quadratic fields, Invent. Math. 93 (1988), 701–713.Google Scholar
Schur, I., Untersuchungen über die Darstellung der endlichen Gruppen durch gebrochene lineare Substitutionen, J. Reine Angew. Math. 29 (1907), 85–137.Google Scholar
Serre, J.-P., Linear representations of finite groups, Graduate Texts in Mathematics, vol. 42 (Springer, 1977).Google Scholar
Shimura, G., Introduction to the arithmetic theory of automorphic functions (Iwanami-Shoten and Princeton University Press, 1971).Google Scholar
Skinner, C. M. and Wiles, A. J., Residually reducible representations and modular forms, Publ. Math. Inst. Hautes Études Sci. 89 (1999), 5–126.Google Scholar
Tilouine, J., Sur la conjecture principale anticyclotomique, Duke Math. J. 59 (1989), 629–673.Google Scholar
Vignéras, M.-F., Représentations modulaires de GL(2, F) en caractéristique l, F corps p-adique, p≠l, Compositio Math. 72 (1989), 33–66.Google Scholar
Weil, A., Exercices dyadiques, Invent. Math. 27 (1974), 1–22; Œuvres III, [1974e]).Google Scholar
Zassenhaus, H., The theory of groups (Courier Dover, 1999).Google Scholar
Zhao, B., Local indecomposability of Hilbert modular Galois representations, Ann. Inst. Fourier (Grenoble) to appear; arXiv:1204.4007v1 [math.NT].Google Scholar