Research Article
A Ramsey-Type Theorem in the Plane
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 127-135
-
- Article
- Export citation
Perfect Hashing and Probability
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 407-409
-
- Article
- Export citation
Front matter
CPC volume 3 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f3
-
- Article
-
- You have access
- Export citation
Research Article
Randomised Approximation in the Tutte Plane
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 137-143
-
- Article
- Export citation
Back matter
CPC volume 3 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation
Research Article
Almost Safe Group Testing with Few Tests†
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 411-419
-
- Article
- Export citation
An Extension of Foster's Network Theorem
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. 421-427
-
- Article
- Export citation
Front matter
CPC volume 3 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
CPC volume 3 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation
Front matter
CPC volume 3 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 12 September 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
CPC volume 3 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 12 September 2008, p. b1
-
- Article
-
- You have access
- Export citation

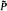 ,
,