Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-18T20:27:20.009Z Has data issue: false hasContentIssue false
  • English
  • Français

Singularity of sparse random matrices: simple proofs

Part of: Probability theory on algebraic and topological structures

Published online by Cambridge University Press:  15 June 2021

Asaf Ferber ,
Matthew Kwan  and
Lisa Sauermann
Asaf Ferber*
Affiliation:
Department of Mathematics, University of California, Irvine, CA92697, USA
Matthew Kwan
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA94305, USA
Lisa Sauermann
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ08540, USA
*
*Corresponding author. Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a random 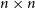$n\times n$ zero-one matrix with ‘sparsity’ p, sampled according to one of the following two models: either every entry is independently taken to be one with probability p (the ‘Bernoulli’ model) or each row is independently uniformly sampled from the set of all length-n zero-one vectors with exactly pn ones (the ‘combinatorial’ model). We give simple proofs of the (essentially best-possible) fact that in both models, if 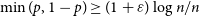$\min(p,1-p)\geq (1+\varepsilon)\log n/n$ for any constant 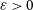$\varepsilon>0$, then our random matrix is nonsingular with probability 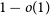$1-o(1)$. In the Bernoulli model, this fact was already well known, but in the combinatorial model this resolves a conjecture of Aigner-Horev and Person.

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 21 - 28
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by NSF Awards DMS-1954395 and DMS-1953799.

‡

Research supported by NSF Award DMS-1953990.

§

Research supported by NSF Grant CCF-1900460 and NSF Award DMS-2100157.

References

Addario-Berry, L. and Eslava, L. (2014) Hitting time theorems for random matrices. Combin. Probab. Comput. 23(5) 635–669.CrossRefGoogle Scholar
Aigner-Horev, E. and Person, Y. (2020) On sparse random combinatorial matrices. arXiv preprint arXiv:2010.07648.Google Scholar
Basak, A. and Rudelson, M. (2018) Sharp transition of the invertibility of the adjacency matrices of sparse random graphs. arXiv preprint arXiv:1809.08454.Google Scholar
Campos, M., Mattos, L., Morris, R. and Morrison, N. On the singularity of random symmetric matrices. Duke Math. J. 170(5) 881–907.Google Scholar
Costello, K. P. and Vu, V. H. (2008) The rank of random graphs. Random Struct. Alg. 33(3) 269–285.CrossRefGoogle Scholar
Costello, K. P. and Vu, V. (2010) On the rank of random sparse matrices. Combin. Probab. Comput. 19(3) 321–342.Google Scholar
ErdÖs, P. (1945) On a lemma of Littlewood and Offord. Bull. Amer. Math. Soc. 51 898–902.Google Scholar
Ferber, A. (2020) Singularity of random symmetric matrices – simple proof. arXiv preprint arXiv:2006.07439.Google Scholar
Ferber, A. and Jain, V. (2019) Singularity of random symmetric matrices—a combinatorial approach to improved bounds. Forum Math. Sigma 7 e22.CrossRefGoogle Scholar
Ferber, A., Jain, V., Luh, K. and Samotij, W. (to appear) On the counting problem in inverse Littlewood–Offord theory. J. Lond. Math. Soc.Google Scholar
Huang, J. (2018) Invertibility of adjacency matrices for random d -regular graphs. arXiv preprint arXiv:1807.06465.Google Scholar
Jain, V. (to appear) Approximate Spielman-Teng theorems for the least singular value of random combinatorial matrices Israel J. Math.Google Scholar
Jain, V., Sah, A. and Sawhney, M. (2020) Singularity of discrete random matrices II. arXiv preprint arXiv:2010.06554.Google Scholar
Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs, Wiley-Interscience Series in Discrete Mathematics and Optimization. Wiley-Interscience, New York.CrossRefGoogle Scholar
KomlÓs, J. (1967) On the determinant of $(0,\,1)$ matrices. Studia Sci. Math. Hungar. 2 7–21.Google Scholar
KomlÓs, J. (1968) On the determinant of random matrices. Studia Sci. Math. Hungar. 3 387–399.Google Scholar
Litvak, A. E., Lytova, A., Tikhomirov, K., Tomczak-Jaegermann, N. & Youssef, P. (2017) Adjacency matrices of random digraphs: singularity and anti-concentration. J. Math. Anal. Appl. 445(2) 1447–1491.CrossRefGoogle Scholar
MÉszÁros, A. (2020) The distribution of sandpile groups of random regular graphs. Trans. Amer. Math. Soc. 373(9) 6529–6594.CrossRefGoogle Scholar
Nguyen, H. H. (2013) On the singularity of random combinatorial matrices. SIAM J. Discrete Math. 27(1) 447–458.CrossRefGoogle Scholar
Nguyen, H. H. and Wood, M. M. (2018) Cokernels of adjacency matrices of random $ r $-regular graphs. arXiv preprint arXiv:1806.10068.Google Scholar
Nguyen, H. H. and Wood, M. M. (2018) Random integral matrices: universality of surjectivity and the cokernel. arXiv preprint arXiv:1806.00596.Google Scholar
Rudelson, M. and Vershynin, R. (2008) The Littlewood-Offord problem and invertibility of random matrices. Adv. Math. 218(2) 600–633.CrossRefGoogle Scholar
Tran, T. (2020) The smallest singular value of random combinatorial matrices. arXiv preprint arXiv:2007.06318.Google Scholar