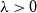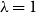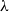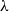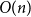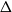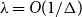1. Introduction
This paper studies the mixing time of the Glauber dynamics for the hard-core model assuming that the underlying graph is an arbitrary tree. In the hard-core model, we are given a graph
![]() $G=(V,E)$
and an activity
$G=(V,E)$
and an activity
![]() $\lambda \gt 0$
. The model is defined on the collection of all independent sets of
$\lambda \gt 0$
. The model is defined on the collection of all independent sets of
![]() $G$
(regardless of size), which we denote as
$G$
(regardless of size), which we denote as
![]() $\Omega$
. Each independent set
$\Omega$
. Each independent set
![]() $\sigma \in \Omega$
is assigned a weight
$\sigma \in \Omega$
is assigned a weight
![]() $w(\sigma )=\lambda ^{|\sigma |}$
where
$w(\sigma )=\lambda ^{|\sigma |}$
where
![]() $|\sigma |$
is the number of vertices contained in the independent set
$|\sigma |$
is the number of vertices contained in the independent set
![]() $\sigma$
. The Gibbs distribution
$\sigma$
. The Gibbs distribution
![]() $\mu$
is defined on
$\mu$
is defined on
![]() $\Omega$
: for
$\Omega$
: for
![]() $\sigma \in \Omega$
, let
$\sigma \in \Omega$
, let
![]() $\mu (\sigma )=w(\sigma )/Z$
where
$\mu (\sigma )=w(\sigma )/Z$
where
![]() $Z=\sum _{\tau \in \Omega } w(\tau )$
is known as the partition function. When
$Z=\sum _{\tau \in \Omega } w(\tau )$
is known as the partition function. When
![]() $\lambda =1$
then every independent set has weight one and hence the Gibbs distribution
$\lambda =1$
then every independent set has weight one and hence the Gibbs distribution
![]() $\mu$
is the uniform distribution over (unweighted) independent sets.
$\mu$
is the uniform distribution over (unweighted) independent sets.
Our goal is to sample from
![]() $\mu$
(or estimate
$\mu$
(or estimate
![]() $Z$
) in time polynomial in
$Z$
) in time polynomial in
![]() $n=|V|$
. Our focus is on trees. These sampling and counting problems are computationally easy on trees using dynamic programming algorithms. Nevertheless, our interest is to understand the convergence properties of a simple Markov Chain Monte Carlo (MCMC) algorithm known as the Glauber dynamics for sampling from the Gibbs distribution.
$n=|V|$
. Our focus is on trees. These sampling and counting problems are computationally easy on trees using dynamic programming algorithms. Nevertheless, our interest is to understand the convergence properties of a simple Markov Chain Monte Carlo (MCMC) algorithm known as the Glauber dynamics for sampling from the Gibbs distribution.
The Glauber dynamics (also known as the Gibbs sampler) is the simple single-site update Markov chain for sampling from the Gibbs distribution of a graphical model. For the hard-core model with activity
![]() $\lambda$
, the transitions
$\lambda$
, the transitions
![]() $X_t\rightarrow X_{t+1}$
of the Glauber dynamics are defined as follows: first, choose a random vertex
$X_t\rightarrow X_{t+1}$
of the Glauber dynamics are defined as follows: first, choose a random vertex
![]() $v$
. Then, with probability
$v$
. Then, with probability
![]() $\frac{\lambda }{1+\lambda }$
set
$\frac{\lambda }{1+\lambda }$
set
![]() $X{^\prime}=X_t\cup \{v\}$
and with the complementary probability set
$X{^\prime}=X_t\cup \{v\}$
and with the complementary probability set
![]() $X{^\prime}=X_t\setminus \{v\}$
. If
$X{^\prime}=X_t\setminus \{v\}$
. If
![]() $X{^\prime}$
is an independent set, then set
$X{^\prime}$
is an independent set, then set
![]() $X_{t+1}=X{^\prime}$
and otherwise set
$X_{t+1}=X{^\prime}$
and otherwise set
![]() $X_{t+1}=X_t$
.
$X_{t+1}=X_t$
.
We consider two standard notions of convergence to stationarity. The relaxation time is the inverse spectral gap, i.e.,
![]() $(1-\lambda ^*)^{-1}$
where
$(1-\lambda ^*)^{-1}$
where
![]() $\lambda ^*=\max \{\lambda _2,|\lambda _N|\}$
and
$\lambda ^*=\max \{\lambda _2,|\lambda _N|\}$
and
![]() $1 = \lambda _1 \gt \lambda _2\geq \dots \geq \lambda _N\gt -1$
are the eigenvalues of the transition matrix
$1 = \lambda _1 \gt \lambda _2\geq \dots \geq \lambda _N\gt -1$
are the eigenvalues of the transition matrix
![]() $P$
for the Glauber dynamics. The relaxation time is a key quantity in the running time for approximate counting algorithms (see, e.g., Štefankovič, Vempala, and Vigoda [Reference Štefankovič, Vempala and Vigoda33]). The mixing time is the number of steps, from the worst initial state, to reach within total variation distance
$P$
for the Glauber dynamics. The relaxation time is a key quantity in the running time for approximate counting algorithms (see, e.g., Štefankovič, Vempala, and Vigoda [Reference Štefankovič, Vempala and Vigoda33]). The mixing time is the number of steps, from the worst initial state, to reach within total variation distance
![]() $\leq 1/2e$
of the stationary distribution, which in our case is the Gibbs distribution
$\leq 1/2e$
of the stationary distribution, which in our case is the Gibbs distribution
![]() $\mu$
.
$\mu$
.
We say that
![]() $O(n)$
is the optimal relaxation time and that
$O(n)$
is the optimal relaxation time and that
![]() $O(n\log{n})$
is the optimal mixing time (see Hayes and Sinclair [Reference Hayes and Sinclair22] for a matching lower bound for any constant-degree graph). Here,
$O(n\log{n})$
is the optimal mixing time (see Hayes and Sinclair [Reference Hayes and Sinclair22] for a matching lower bound for any constant-degree graph). Here,
![]() $n$
denotes the size of the underlying graph. More generally, we say the Glauber dynamics is rapidly mixing when the mixing time is
$n$
denotes the size of the underlying graph. More generally, we say the Glauber dynamics is rapidly mixing when the mixing time is
![]() $\mathrm{poly}(n)$
.
$\mathrm{poly}(n)$
.
We establish bounds on the mixing time of the Glauber dynamics by means of approximate tensorization inequalities for the variance of the hard-core model. Interestingly, our analysis utilises nothing further than the inductive nature of the tree, e.g., we do not make any assumptions about spatial mixing properties of the Gibbs distribution. As a consequence, the bounds we obtain have no dependence on the maximum degree of the graph.
To be more specific we derive the following two group of results: We establish approximate tensorization of variance of the hard-core model on the tree for all
![]() $\lambda \lt 1.1$
. This implies optimal
$\lambda \lt 1.1$
. This implies optimal
![]() $O(n)$
relaxation time for the Glauber dynamics. Notably this also includes the uniform distribution over independent sets, i.e.,
$O(n)$
relaxation time for the Glauber dynamics. Notably this also includes the uniform distribution over independent sets, i.e.,
![]() $\lambda =1$
.
$\lambda =1$
.
We can now state our main results.
Theorem 1.1.
For any
![]() $n$
-vertex tree, for any
$n$
-vertex tree, for any
![]() $\lambda \lt 1.1$
the Glauber dynamics for sampling
$\lambda \lt 1.1$
the Glauber dynamics for sampling
![]() $\lambda$
-weighted independent sets in the hard-core model has an optimal relaxation time of
$\lambda$
-weighted independent sets in the hard-core model has an optimal relaxation time of
![]() $O(n)$
.
$O(n)$
.
We believe the optimal mixing results of Theorem1.1 are related to the reconstruction threshold, which we describe now. Consider the complete
![]() $\Delta$
-regular tree of height
$\Delta$
-regular tree of height
![]() $h$
; this is the rooted tree where all nodes at distance
$h$
; this is the rooted tree where all nodes at distance
![]() $\ell \lt h$
from the root have
$\ell \lt h$
from the root have
![]() $\Delta -1$
children and all nodes at distance
$\Delta -1$
children and all nodes at distance
![]() $h$
from the root are leaves. We are interested in how the configuration at the leaves affects the configuration at the root.
$h$
from the root are leaves. We are interested in how the configuration at the leaves affects the configuration at the root.
Consider fixing an assignment/configuration
![]() $\sigma$
to the leaves (i.e., specifying which leaves are fixed to occupied and which are unoccupied), we refer to this fixed assignment to the leaves as a boundary condition
$\sigma$
to the leaves (i.e., specifying which leaves are fixed to occupied and which are unoccupied), we refer to this fixed assignment to the leaves as a boundary condition
![]() $\sigma$
. Let
$\sigma$
. Let
![]() $\mu _\sigma$
denote the Gibbs distribution conditional on this fixed boundary condition
$\mu _\sigma$
denote the Gibbs distribution conditional on this fixed boundary condition
![]() $\sigma$
, and let
$\sigma$
, and let
![]() $p_\sigma$
denote the marginal probability that the root is occupied in
$p_\sigma$
denote the marginal probability that the root is occupied in
![]() $\mu _\sigma$
.
$\mu _\sigma$
.
The uniqueness threshold
![]() $\lambda _c(\Delta )$
measures the affect of the worst-case boundary condition on the root. For all
$\lambda _c(\Delta )$
measures the affect of the worst-case boundary condition on the root. For all
![]() $\lambda \lt \lambda _c(\Delta )$
, all
$\lambda \lt \lambda _c(\Delta )$
, all
![]() $\sigma \neq \sigma ^{\prime}$
, in the limit
$\sigma \neq \sigma ^{\prime}$
, in the limit
![]() $h\rightarrow \infty$
, we have
$h\rightarrow \infty$
, we have
![]() $p_\sigma =p_\sigma ^{\prime}$
; this is known as the (tree) uniqueness region. In contrast, for
$p_\sigma =p_\sigma ^{\prime}$
; this is known as the (tree) uniqueness region. In contrast, for
![]() $\lambda \gt \lambda _c(\Delta )$
there are pairs
$\lambda \gt \lambda _c(\Delta )$
there are pairs
![]() $\sigma \neq \sigma ^{\prime}$
(namely, all even occupied vs. odd occupied) for which the limits are different; this is the non-uniqueness region. The uniqueness threshold is at
$\sigma \neq \sigma ^{\prime}$
(namely, all even occupied vs. odd occupied) for which the limits are different; this is the non-uniqueness region. The uniqueness threshold is at
![]() $\lambda _c(\Delta )=(\Delta -1)^{\Delta -1}/(\Delta -2)^{\Delta } = O(1/\Delta )$
.
$\lambda _c(\Delta )=(\Delta -1)^{\Delta -1}/(\Delta -2)^{\Delta } = O(1/\Delta )$
.
In contrast, the reconstruction threshold
![]() $\lambda _r(\Delta )$
measures the affect on the root of a random/typical boundary condition. In particular, we fix an assignment
$\lambda _r(\Delta )$
measures the affect on the root of a random/typical boundary condition. In particular, we fix an assignment
![]() $c$
at the root and then generate the Gibbs distribution via an appropriately defined broadcasting process. Finally, we fix the boundary configuration
$c$
at the root and then generate the Gibbs distribution via an appropriately defined broadcasting process. Finally, we fix the boundary configuration
![]() $\sigma$
and ask whether, in the conditional Gibbs distribution
$\sigma$
and ask whether, in the conditional Gibbs distribution
![]() $\mu _\sigma$
, the root has a bias towards the initial assignment
$\mu _\sigma$
, the root has a bias towards the initial assignment
![]() $c$
. The non-reconstruction region
$c$
. The non-reconstruction region
![]() $\lambda \lt \lambda _r(\Delta )$
corresponds to when we cannot infer the root’s initial value, in expectation over the choice of the boundary configuration
$\lambda \lt \lambda _r(\Delta )$
corresponds to when we cannot infer the root’s initial value, in expectation over the choice of the boundary configuration
![]() $\sigma$
and in the limit
$\sigma$
and in the limit
![]() $h\rightarrow \infty$
, see Mossel [Reference Mossel28] for a more complete introduction to reconstruction.
$h\rightarrow \infty$
, see Mossel [Reference Mossel28] for a more complete introduction to reconstruction.
The reconstruction threshold is not known exactly but close bounds were established by Bhatnagar, Sly, and Tetali [Reference Bhatnagar, Sly and Tetali3] and Brightwell and Winkler [Reference Brightwell and Winkler5]; they showed that for constants
![]() $C_1,C_2\gt 0$
and sufficiently large
$C_1,C_2\gt 0$
and sufficiently large
![]() $\Delta$
:
$\Delta$
:
![]() $C_1\log ^2{\Delta }/\log \log{\Delta }\leq \lambda _r(\Delta )\leq C_2\log ^2{\Delta }$
, and hence
$C_1\log ^2{\Delta }/\log \log{\Delta }\leq \lambda _r(\Delta )\leq C_2\log ^2{\Delta }$
, and hence
![]() $\lambda _r(\Delta )$
is “increasing asymptotically” with
$\lambda _r(\Delta )$
is “increasing asymptotically” with
![]() $\Delta$
whereas the uniqueness threshold is a decreasing function of
$\Delta$
whereas the uniqueness threshold is a decreasing function of
![]() $\Delta$
. Martin [Reference Martin25] showed that
$\Delta$
. Martin [Reference Martin25] showed that
![]() $\lambda _r(\Delta )\gt e-1$
for all
$\lambda _r(\Delta )\gt e-1$
for all
![]() $\Delta$
. As a consequence, we conjecture that Theorem1.1 holds for all trees for all
$\Delta$
. As a consequence, we conjecture that Theorem1.1 holds for all trees for all
![]() $\lambda \lt e-1$
, which is close to the bound we obtain. A slowdown in the reconstruction region is known: Restrepo, Štefankovič, Vera, Vigoda, and Yang [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] showed that there are trees for which there is a polynomial slow down for
$\lambda \lt e-1$
, which is close to the bound we obtain. A slowdown in the reconstruction region is known: Restrepo, Štefankovič, Vera, Vigoda, and Yang [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] showed that there are trees for which there is a polynomial slow down for
![]() $\lambda \gt C$
for a constant
$\lambda \gt C$
for a constant
![]() $C\gt 0$
; an explicit constant
$C\gt 0$
; an explicit constant
![]() $C$
is not stated in [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] but using the Kesten–Stigum bound one can show
$C$
is not stated in [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] but using the Kesten–Stigum bound one can show
![]() $C\approx 28$
(by considering binary trees).
$C\approx 28$
(by considering binary trees).
For general graphs the appropriate threshold is the uniqueness threshold, which is
![]() $\lambda _c(\Delta )=O(1/\Delta )$
. In particular, for bipartite random
$\lambda _c(\Delta )=O(1/\Delta )$
. In particular, for bipartite random
![]() $\Delta$
-regular graphs the Glauber dynamics has optimal mixing in the uniqueness region by Chen, Liu and Vigoda [Reference Chen, Liu and Vigoda16], and is exponentially slow in the non-uniqueness region by Mossel, Weitz, and Wormald [Reference Mossel, Weitz and Wormald29] (see also [Reference Galanis, Štefankovič and Vigoda21]). Moreover, for general graphs there is a computational phase transition at the uniqueness threshold: optimal mixing on all graphs of maximum degree
$\Delta$
-regular graphs the Glauber dynamics has optimal mixing in the uniqueness region by Chen, Liu and Vigoda [Reference Chen, Liu and Vigoda16], and is exponentially slow in the non-uniqueness region by Mossel, Weitz, and Wormald [Reference Mossel, Weitz and Wormald29] (see also [Reference Galanis, Štefankovič and Vigoda21]). Moreover, for general graphs there is a computational phase transition at the uniqueness threshold: optimal mixing on all graphs of maximum degree
![]() $\Delta$
in the uniqueness region [Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12,Reference Chen, Liu and Vigoda16], and NP-hardness to approximately count/sample in the non-uniqueness region by Sly [Reference Sly31] (see also, [Reference Galanis, Štefankovič and Vigoda21,Reference Sly and Sun32]).
$\Delta$
in the uniqueness region [Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12,Reference Chen, Liu and Vigoda16], and NP-hardness to approximately count/sample in the non-uniqueness region by Sly [Reference Sly31] (see also, [Reference Galanis, Štefankovič and Vigoda21,Reference Sly and Sun32]).
There are a variety of mixing results for the special case on trees, which is the focus of this paper. In terms of establishing optimal mixing time bounds for the Glauber dynamics, previous results only applied to complete,
![]() $\Delta$
-regular trees. Seminal work of Martinelli, Sinclair, and Weitz [Reference Martinelli, Sinclair and Weitz26,Reference Martinelli, Sinclair and Weitz27] proved optimal mixing on complete
$\Delta$
-regular trees. Seminal work of Martinelli, Sinclair, and Weitz [Reference Martinelli, Sinclair and Weitz26,Reference Martinelli, Sinclair and Weitz27] proved optimal mixing on complete
![]() $\Delta$
-regular trees for all
$\Delta$
-regular trees for all
![]() $\lambda$
. The intuitive reason this holds for all
$\lambda$
. The intuitive reason this holds for all
![]() $\lambda$
is that the complete tree corresponds to one of the two extremal phases (all even boundary or all odd boundary) and hence it does not exhibit the phase co-existence which causes mixing. As mentioned earlier, [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] shows that there is a fixed assignment
$\lambda$
is that the complete tree corresponds to one of the two extremal phases (all even boundary or all odd boundary) and hence it does not exhibit the phase co-existence which causes mixing. As mentioned earlier, [Reference Restrepo, Štefankovič, Vera, Vigoda and Yang30] shows that there is a fixed assignment
![]() $\tau$
for the leaves of the complete,
$\tau$
for the leaves of the complete,
![]() $\Delta$
-regular tree so that the mixing time slows down in the reconstruction region; intuitively, this boundary condition
$\Delta$
-regular tree so that the mixing time slows down in the reconstruction region; intuitively, this boundary condition
![]() $\tau$
corresponds to the assignment obtained by the broadcasting process.
$\tau$
corresponds to the assignment obtained by the broadcasting process.
For more general trees the following results were known. A classical result of Berger, Kenyon, Mossel and Peres [Reference Berger, Kenyon, Mossel and Peres2] proves polynomial mixing time for trees with constant maximum degree [Reference Berger, Kenyon, Mossel and Peres2]. A very recent result of Eppstein and Frishberg [Reference Eppstein and Frishberg19] proved polynomial mixing time
![]() $n^{C(\lambda )}$
of the Glauber dynamics for graphs with bounded tree-width which includes arbitrary trees, however the polynomial exponent is
$n^{C(\lambda )}$
of the Glauber dynamics for graphs with bounded tree-width which includes arbitrary trees, however the polynomial exponent is
![]() $C(\lambda )=O(1+|\log (\lambda )|)$
for trees; see more recent work of Chen [Reference Chen10] for further improvements. For other combinatorial models, rapid mixing for the Glauber dynamics on trees with bounded maximum degree was established for
$C(\lambda )=O(1+|\log (\lambda )|)$
for trees; see more recent work of Chen [Reference Chen10] for further improvements. For other combinatorial models, rapid mixing for the Glauber dynamics on trees with bounded maximum degree was established for
![]() $k$
-colorings in [Reference Lucier, Molloy and Peres24] and edge-colorings in [Reference Delcourt, Heinrich and Perarnau18].
$k$
-colorings in [Reference Lucier, Molloy and Peres24] and edge-colorings in [Reference Delcourt, Heinrich and Perarnau18].
Spectral independence is a powerful notion in the analysis of the convergence rate of MCMC algorithms. For independent sets on an
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $G=(V,E)$
, spectral independence considers the
$G=(V,E)$
, spectral independence considers the
![]() $n\times n$
pairwise influence matrix
$n\times n$
pairwise influence matrix
![]() ${\mathcal{I}}_G$
where
${\mathcal{I}}_G$
where
![]() ${\mathcal{I}}_G(v,w)=\mathrm{Prob}_{\sigma \sim \mu }(v\in \sigma \ |\ w\in \sigma )-\mathrm{Prob}_{\sigma \sim \mu }(v\in \sigma \ |\ w\notin \sigma )$
; this matrix is closely related to the vertex covariance matrix. We say that spectral independence holds if the maximum eigenvalue of
${\mathcal{I}}_G(v,w)=\mathrm{Prob}_{\sigma \sim \mu }(v\in \sigma \ |\ w\in \sigma )-\mathrm{Prob}_{\sigma \sim \mu }(v\in \sigma \ |\ w\notin \sigma )$
; this matrix is closely related to the vertex covariance matrix. We say that spectral independence holds if the maximum eigenvalue of
![]() ${\mathcal{I}}_{G{^\prime}}$
for all vertex-induced subgraphs
${\mathcal{I}}_{G{^\prime}}$
for all vertex-induced subgraphs
![]() $G{^\prime}$
of
$G{^\prime}$
of
![]() $G$
are bounded by a constant. Spectral independence was introduced by Anari, Liu, and Oveis Gharan [Reference Anari, Liu and Gharan1]. Chen, Liu, and Vigoda [Reference Chen, Liu and Vigoda16] proved that spectral independence, together with a simple condition known as marginal boundedness which is a lower bound on the marginal probability of a valid vertex-spin pair, implies optimal mixing time of the Glauber dynamics for constant-degree graphs. This has led to a flurry of optimal mixing results, e.g., [Reference Blanca, Caputo, Chen, Parisi, Štefankovič and Vigoda4,Reference Chen and Gu14,Reference Chen, Liu, Mani and Moitra15,Reference Chen, Liu and Vigoda17,Reference Liu23].
$G$
are bounded by a constant. Spectral independence was introduced by Anari, Liu, and Oveis Gharan [Reference Anari, Liu and Gharan1]. Chen, Liu, and Vigoda [Reference Chen, Liu and Vigoda16] proved that spectral independence, together with a simple condition known as marginal boundedness which is a lower bound on the marginal probability of a valid vertex-spin pair, implies optimal mixing time of the Glauber dynamics for constant-degree graphs. This has led to a flurry of optimal mixing results, e.g., [Reference Blanca, Caputo, Chen, Parisi, Štefankovič and Vigoda4,Reference Chen and Gu14,Reference Chen, Liu, Mani and Moitra15,Reference Chen, Liu and Vigoda17,Reference Liu23].
The limitation of the above spectral independence results is that they only hold for graphs with constant maximum degree
![]() $\Delta$
. There are several noteworthy results that achieve a stronger form of spectral independence which establishes optimal mixing for unbounded degree graphs [Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12]; however all of these results for general graphs only achieve rapid mixing in the tree uniqueness region which corresponds to
$\Delta$
. There are several noteworthy results that achieve a stronger form of spectral independence which establishes optimal mixing for unbounded degree graphs [Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12]; however all of these results for general graphs only achieve rapid mixing in the tree uniqueness region which corresponds to
![]() $\lambda =O(1/\Delta )$
whereas we are aiming for
$\lambda =O(1/\Delta )$
whereas we are aiming for
![]() $\lambda =\Theta (1)$
.
$\lambda =\Theta (1)$
.
The inductive approach we use to establish approximate tensorization inequalities can also be utilised to establish spectral independence. In fact, we show that spectral independence holds for any tree when
![]() $\lambda \lt 1.3$
, including the case where
$\lambda \lt 1.3$
, including the case where
![]() $\lambda =1$
, see Section 4. Applying the results of Anari, Liu, and Oveis Gharan [Reference Anari, Liu and Gharan1] we obtain a
$\lambda =1$
, see Section 4. Applying the results of Anari, Liu, and Oveis Gharan [Reference Anari, Liu and Gharan1] we obtain a
![]() $\mathrm{poly}(n)$
bound on the mixing time, but with a large constant in the exponent of
$\mathrm{poly}(n)$
bound on the mixing time, but with a large constant in the exponent of
![]() $n$
. For constant-degree trees we obtain the following optimal mixing result by applying the results of Chen, Liu, and Vigoda [Reference Chen, Liu and Vigoda16] (see also [Reference Blanca, Caputo, Chen, Parisi, Štefankovič and Vigoda4,Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12]).
$n$
. For constant-degree trees we obtain the following optimal mixing result by applying the results of Chen, Liu, and Vigoda [Reference Chen, Liu and Vigoda16] (see also [Reference Blanca, Caputo, Chen, Parisi, Štefankovič and Vigoda4,Reference Chen and Eldan11,Reference Chen, Feng, Yin and Zhang12]).
Theorem 1.2.
For all constant
![]() $\Delta$
, all
$\Delta$
, all
![]() $\lambda \leq 1.3$
, for any tree
$\lambda \leq 1.3$
, for any tree
![]() $T$
with maximum degree
$T$
with maximum degree
![]() $\Delta$
, the Glauber dynamics for sampling
$\Delta$
, the Glauber dynamics for sampling
![]() $\lambda$
-weighted independent sets has an optimal mixing time of
$\lambda$
-weighted independent sets has an optimal mixing time of
![]() $O(n\log{n})$
.
$O(n\log{n})$
.
Interestingly, combining the spectral independence results from the proof Theorem1.2 with results of Chen, Feng, Yin, and Zhang [[Reference Chen, Feng, Yin and Zhang13], Theorem 1.9], we are able to strengthen Theorem1.1 by allowing larger fugacities, i.e.,
![]() $\lambda \leq 1.3$
.
$\lambda \leq 1.3$
.
Corollary 1.3.
For any
![]() $n$
-vertex tree, for any
$n$
-vertex tree, for any
![]() $\lambda \leq 1.3$
the Glauber dynamics for sampling
$\lambda \leq 1.3$
the Glauber dynamics for sampling
![]() $\lambda$
-weighted independent sets in the hard-core model has an optimal relaxation time of
$\lambda$
-weighted independent sets in the hard-core model has an optimal relaxation time of
![]() $O(n)$
.
$O(n)$
.
In the next section we recall the key functional definitions and basic properties of variance that will be useful later in the proofs. In Section 3 we prove approximate tensorization of variance which establishes Theorem1.1. We establish spectral independence and prove Theorem1.2 in Section 4.
Remark 1.4. An earlier version of this paper [Reference Efthymiou, C., Hayes, T. P., Štefankovič, D. and Vigoda, E.20] claimed to prove
![]() $O(n\log{n})$
mixing time for
$O(n\log{n})$
mixing time for
![]() $\lambda \leq .44$
for any tree (without any constraint on the maximum degree). There was a mistake in that proof. In particular, inequality (54) is false. Moreover, Zongchen Chen pointed out a simple test function
$\lambda \leq .44$
for any tree (without any constraint on the maximum degree). There was a mistake in that proof. In particular, inequality (54) is false. Moreover, Zongchen Chen pointed out a simple test function
![]() $f$
which shows that entropy tensorization and modified log-Sobolev inequality do not hold for the star graph with constants independent of the degree.
$f$
which shows that entropy tensorization and modified log-Sobolev inequality do not hold for the star graph with constants independent of the degree.
A recent paper of Chen, Yang, Yin, and Zhang [Reference Chen, Yang, Yin and Zhang9] improves Corollary 1.3 to obtain optimal relaxation time on trees for
![]() $\lambda \lt e^2$
.
$\lambda \lt e^2$
.
2. Preliminaries
2.1 Standard definitions
Let
![]() $P$
be the transition matrix of a Markov chain
$P$
be the transition matrix of a Markov chain
![]() $\{X_t\}$
with a finite state space
$\{X_t\}$
with a finite state space
![]() $\Omega$
and equilibrium distribution
$\Omega$
and equilibrium distribution
![]() $\mu$
. For
$\mu$
. For
![]() $t\geq 0$
and
$t\geq 0$
and
![]() $\sigma \in \Omega$
, let
$\sigma \in \Omega$
, let
![]() $P^{t}(\sigma, \cdot )$
denote the distribution of
$P^{t}(\sigma, \cdot )$
denote the distribution of
![]() $X_t$
when the initial state of the chain satisfies
$X_t$
when the initial state of the chain satisfies
![]() $X_0=\sigma$
. The mixing time of the Markov chain
$X_0=\sigma$
. The mixing time of the Markov chain
![]() $\{X_t\}_{t \geq 0}$
is defined by
$\{X_t\}_{t \geq 0}$
is defined by
The transition matrix
![]() $P$
with stationary distribution
$P$
with stationary distribution
![]() $\mu$
is called time reversible if it satisfies the so-called detailed balance relation, i.e., for any
$\mu$
is called time reversible if it satisfies the so-called detailed balance relation, i.e., for any
![]() $x, y\in \Omega$
we have
$x, y\in \Omega$
we have
![]() $\mu (x)P(x,y)=P(y,x)\mu (y)$
. For
$\mu (x)P(x,y)=P(y,x)\mu (y)$
. For
![]() $P$
that is time reversible the set of eigenvalues are real numbers and we denote them as
$P$
that is time reversible the set of eigenvalues are real numbers and we denote them as
![]() $1=\lambda _1\geq \lambda _2\geq \ldots \lambda _{|\Omega |}\geq -1$
. Let
$1=\lambda _1\geq \lambda _2\geq \ldots \lambda _{|\Omega |}\geq -1$
. Let
![]() $\lambda ^*=\max \{|\lambda _2|, |\lambda _{|\Omega |}|\}$
, then we define the relaxation time
$\lambda ^*=\max \{|\lambda _2|, |\lambda _{|\Omega |}|\}$
, then we define the relaxation time
![]() $T_{\text{relax}}$
by
$T_{\text{relax}}$
by
The quantity
![]() $1-\lambda ^*$
is also known as the spectral gap of
$1-\lambda ^*$
is also known as the spectral gap of
![]() $P$
. We use
$P$
. We use
![]() $T_{\text{relax}}$
to bound
$T_{\text{relax}}$
to bound
![]() $T_{\text{mix}}$
by using the following inequality
$T_{\text{mix}}$
by using the following inequality
2.2 Gibbs distributions and functional analytic definitions
For a graph
![]() $G=(V,E)$
and
$G=(V,E)$
and
![]() $\lambda \gt 0$
, let
$\lambda \gt 0$
, let
![]() $\mu =\mu _{G,\lambda }$
be the hard-core model on this graph with activity
$\mu =\mu _{G,\lambda }$
be the hard-core model on this graph with activity
![]() $\lambda$
, while let
$\lambda$
, while let
![]() $\Omega \subseteq 2^V$
be the support of
$\Omega \subseteq 2^V$
be the support of
![]() $\mu$
, i.e.,
$\mu$
, i.e.,
![]() $\Omega$
are the collection of independent sets of
$\Omega$
are the collection of independent sets of
![]() $G$
.
$G$
.
For any function
![]() $f\,:\,\Omega \to \mathbb{R}_{\geq 0}$
, we let
$f\,:\,\Omega \to \mathbb{R}_{\geq 0}$
, we let
![]() $\mu (f)$
is the expected value of
$\mu (f)$
is the expected value of
![]() $f$
with respect to
$f$
with respect to
![]() $\mu$
, i.e.,
$\mu$
, i.e.,
Analogously, we define variance of
![]() $f$
with respect to
$f$
with respect to
![]() $\mu$
by
$\mu$
by
We are also using the following equation for
![]() $\mathrm{Var}(f)$
,
$\mathrm{Var}(f)$
,
For any subset
![]() $S \subseteq V$
, let
$S \subseteq V$
, let
![]() $\Omega _S$
denote the set of independent sets on
$\Omega _S$
denote the set of independent sets on
![]() $S$
. Then, let
$S$
. Then, let
![]() $\mu _S$
denote the marginal of
$\mu _S$
denote the marginal of
![]() $\mu$
on
$\mu$
on
![]() $S$
; that is, for any
$S$
; that is, for any
![]() $\sigma \in \Omega _S$
, we have that
$\sigma \in \Omega _S$
, we have that
For any
![]() $S\subset V$
, any
$S\subset V$
, any
![]() $\tau \in \Omega _{V\setminus S}$
, we let
$\tau \in \Omega _{V\setminus S}$
, we let
![]() $\mu ^{\tau }_S$
be the distribution
$\mu ^{\tau }_S$
be the distribution
![]() $\mu$
conditional on the configuration
$\mu$
conditional on the configuration
![]() $\tau$
on
$\tau$
on
![]() $V\setminus S$
, and let
$V\setminus S$
, and let
![]() $\Omega _S^\tau$
to be the support of
$\Omega _S^\tau$
to be the support of
![]() $\mu ^\tau _S$
.
$\mu ^\tau _S$
.
For any
![]() $S \subseteq V$
, for any
$S \subseteq V$
, for any
![]() $\tau \in \Omega _{V \setminus S}$
, we define the function
$\tau \in \Omega _{V \setminus S}$
, we define the function
![]() $f_{\tau }\,:\, \Omega ^{\tau }_S \to \mathbb{R}_{\geq 0}$
such that
$f_{\tau }\,:\, \Omega ^{\tau }_S \to \mathbb{R}_{\geq 0}$
such that
![]() $f_{\tau }(\sigma ) = f(\tau \cup \sigma )$
for all
$f_{\tau }(\sigma ) = f(\tau \cup \sigma )$
for all
![]() $\sigma \in \Omega ^\tau _S$
.
$\sigma \in \Omega ^\tau _S$
.
Let
Let
![]() $\mathrm{Var}_S^\tau (f)$
denote the variance of
$\mathrm{Var}_S^\tau (f)$
denote the variance of
![]() $f_\tau$
with respect to the conditional distribution
$f_\tau$
with respect to the conditional distribution
![]() $\mu ^\tau _S$
:
$\mu ^\tau _S$
:
Furthermore, we let
i.e.,
![]() $\mu (\mathrm{Var}_S(f))$
is the average of
$\mu (\mathrm{Var}_S(f))$
is the average of
![]() $\mathrm{Var}_S^\tau (f)$
with respect to
$\mathrm{Var}_S^\tau (f)$
with respect to
![]() $\tau$
being distributed as in
$\tau$
being distributed as in
![]() $\mu _{V \setminus S}({\cdot})$
. For the sake of brevity, when
$\mu _{V \setminus S}({\cdot})$
. For the sake of brevity, when
![]() $S=\{v\}$
, i.e., the set
$S=\{v\}$
, i.e., the set
![]() $S$
is a singleton, we use
$S$
is a singleton, we use
![]() $\mu (\mathrm{Var}_v(f))$
.
$\mu (\mathrm{Var}_v(f))$
.
Finally, let
i.e.,
![]() $\mathrm{Var}(\mu _S(f))$
is the variance of
$\mathrm{Var}(\mu _S(f))$
is the variance of
![]() $\mu _S^\tau (f)$
with respect to
$\mu _S^\tau (f)$
with respect to
![]() $\tau$
being distributed as in
$\tau$
being distributed as in
![]() $\mu _{V \setminus S}({\cdot})$
.
$\mu _{V \setminus S}({\cdot})$
.
When
![]() $X$
is the following two-valued random variable:
$X$
is the following two-valued random variable:
 \begin{equation*} X = \begin {cases} A & \mbox { with probability $p$} \\ B & \mbox { with probability $1-p$}, \end {cases} \end{equation*}
\begin{equation*} X = \begin {cases} A & \mbox { with probability $p$} \\ B & \mbox { with probability $1-p$}, \end {cases} \end{equation*}
then one formulation for the variance that will be convenient for us is
2.3 Approximate tensorization of variance
To bound the convergence rate of the Glauber dynamics we consider the approximate tensorization of variance as introduced in [Reference Caputo, Menz and Tetali7].
We begin with the definition of approximate tensorization of variance.
Definition 2.1 (Variance Tensorization). A distribution
![]() $\mu$
with support
$\mu$
with support
![]() $\Omega \subseteq \{\pm 1\}^V$
satisfies the approximate tensorisation of Variance with constant
$\Omega \subseteq \{\pm 1\}^V$
satisfies the approximate tensorisation of Variance with constant
![]() $C\gt 0$
, denoted using the predicate
$C\gt 0$
, denoted using the predicate
![]() $VT(C)$
, if for all
$VT(C)$
, if for all
![]() $f\,:\,\Omega \to \mathbb{R}_{\geq 0}$
we have that
$f\,:\,\Omega \to \mathbb{R}_{\geq 0}$
we have that
For a vertex
![]() $x$
, recall that
$x$
, recall that
![]() $\mathrm{Var}_{x}[f]= \sum _{\sigma }\mu _{V\setminus \{x\}}(\sigma )\mathrm{Var}^{\sigma }_{x}[f_{\sigma }]$
. Variance tensorization
$\mathrm{Var}_{x}[f]= \sum _{\sigma }\mu _{V\setminus \{x\}}(\sigma )\mathrm{Var}^{\sigma }_{x}[f_{\sigma }]$
. Variance tensorization
![]() $VT(C)$
yields the following bound on the relaxation time of the Glauber dynamics [Reference Caputo6,Reference Caputo, Menz and Tetali7]:
$VT(C)$
yields the following bound on the relaxation time of the Glauber dynamics [Reference Caputo6,Reference Caputo, Menz and Tetali7]:
2.4 Decomposition of variance
We use the following basic decomposition properties for variance. The following lemma follows from a decomposition of relative entropy, see [[Reference Caputo and Parisi8], Lemma3.1] (see also [[Reference Blanca, Caputo, Chen, Parisi, Štefankovič and Vigoda4], Lemma2.3]).
Lemma 2.2.
For any
![]() $S\subset V$
, for any
$S\subset V$
, for any
![]() $f\geq 0$
:
$f\geq 0$
:
where
![]() $\mathrm{Var}(\mu _S(f))$
is defined in Eq. (6).
$\mathrm{Var}(\mu _S(f))$
is defined in Eq. (6).
We utilise the following variance factorisation for product measures, see [[Reference Caputo6], Eqn (4.7)].
Lemma 2.3.
Consider
![]() $U,W\subset V$
where
$U,W\subset V$
where
![]() $\mathrm{dist}(U,W) \ge 2$
. Then for all
$\mathrm{dist}(U,W) \ge 2$
. Then for all
![]() $f\geq 0$
we have:
$f\geq 0$
we have:
On a first account, the reader might find it challenging to parse the expression
![]() $\mu [\mathrm{Var}_U(\mu _W(f)) ]$
. In that respect, (5) and (6) might be useful. Specifically,
$\mu [\mathrm{Var}_U(\mu _W(f)) ]$
. In that respect, (5) and (6) might be useful. Specifically,
![]() $\mu [\mathrm{Var}_U(\mu _W(f)) ]$
is the expectation of
$\mu [\mathrm{Var}_U(\mu _W(f)) ]$
is the expectation of
![]() $\mathrm{Var}^{\tau }_U(\mu _W(f))$
with respect to
$\mathrm{Var}^{\tau }_U(\mu _W(f))$
with respect to
![]() $\tau$
being distributed as in
$\tau$
being distributed as in
![]() $\mu _{\bar{U}\cap \bar{W}}$
. Furthermore,
$\mu _{\bar{U}\cap \bar{W}}$
. Furthermore,
![]() $\mathrm{Var}^{\tau }_U(\mu _W(f))$
corresponds to the variance of
$\mathrm{Var}^{\tau }_U(\mu _W(f))$
corresponds to the variance of
![]() $\mu _W^{\tau, \sigma }(f)$
with respect to the configurations
$\mu _W^{\tau, \sigma }(f)$
with respect to the configurations
![]() $\tau$
at
$\tau$
at
![]() $V\setminus (U\cup W)$
and
$V\setminus (U\cup W)$
and
![]() $\sigma$
at
$\sigma$
at
![]() $U$
, while
$U$
, while
![]() $\tau$
is fixed and
$\tau$
is fixed and
![]() $\sigma$
is distributed as in
$\sigma$
is distributed as in
![]() $\mu ^{\tau }_{U}({\cdot})$
.
$\mu ^{\tau }_{U}({\cdot})$
.
Proof.
We apply [[Reference Caputo6], Equation (4.7)], which reaches the same conclusion under the assumptions that
![]() $U \cap W = \emptyset$
and
$U \cap W = \emptyset$
and
![]() $\mu _U \mu _W = \mu _W \mu _U$
. In the current context, the reason these conditional expectation operators commute here is that, because
$\mu _U \mu _W = \mu _W \mu _U$
. In the current context, the reason these conditional expectation operators commute here is that, because
![]() $\mathrm{dist}(U,W) \ge 2$
, if we let
$\mathrm{dist}(U,W) \ge 2$
, if we let
![]() $S$
be an independent set sampled according to distribution
$S$
be an independent set sampled according to distribution
![]() $\mu$
, then the random variables
$\mu$
, then the random variables
![]() $S \cap U$
and
$S \cap U$
and
![]() $S \cap W$
are conditionally independent given
$S \cap W$
are conditionally independent given
![]() $S \setminus (U \cup W)$
.
$S \setminus (U \cup W)$
.
3. Variance factorization
In this section we prove Theorem1.1, establishing an optimal bound on the relaxation time for the Glauber dynamics on any tree for
![]() $\lambda \leq 1.1$
. We will prove this by establishing variance tensorization, see Definition 2.1.
$\lambda \leq 1.1$
. We will prove this by establishing variance tensorization, see Definition 2.1.
Consider a graph
![]() $G=(V,E)$
and a collection of fugacities
$G=(V,E)$
and a collection of fugacities
![]() $\lambda _i$
for each
$\lambda _i$
for each
![]() $i\in V$
. Throughout this section we will assume that all the fugacities are bounded by
$i\in V$
. Throughout this section we will assume that all the fugacities are bounded by
![]() $1.1$
. Consider the following more general definition of the Gibbs distribution
$1.1$
. Consider the following more general definition of the Gibbs distribution
![]() $\mu$
for the hard-core model, where for an independent set
$\mu$
for the hard-core model, where for an independent set
![]() $S$
,
$S$
,
Let
![]() $T{^\prime}=(V{^\prime},E{^\prime})$
be a tree, let
$T{^\prime}=(V{^\prime},E{^\prime})$
be a tree, let
![]() $\{\lambda ^{\prime}_w\}_{w\in V^{\prime}}$
be a collection of fugacities and let
$\{\lambda ^{\prime}_w\}_{w\in V^{\prime}}$
be a collection of fugacities and let
![]() $\mu^{\prime}$
be the corresponding Gibbs distribution. We will establish the following variance tensorization inequality: for all
$\mu^{\prime}$
be the corresponding Gibbs distribution. We will establish the following variance tensorization inequality: for all
![]() $f{^\prime}\,:\,2^{V{^\prime}}\rightarrow{\mathbb R}$
$f{^\prime}\,:\,2^{V{^\prime}}\rightarrow{\mathbb R}$
where
![]() $F\,:\,{\mathbb{R}}_{\geq 0}\rightarrow{\mathbb{R}}_{\geq 0}$
is a function to be determined later (in Lemma 3.1). We refer to
$F\,:\,{\mathbb{R}}_{\geq 0}\rightarrow{\mathbb{R}}_{\geq 0}$
is a function to be determined later (in Lemma 3.1). We refer to
![]() $\mathrm{Var}(f{^\prime})$
as the “global” variance and we refer to
$\mathrm{Var}(f{^\prime})$
as the “global” variance and we refer to
![]() $\mu^{\prime}(\mathrm{Var}_x(f{^\prime}))$
as the “local” variance (of
$\mu^{\prime}(\mathrm{Var}_x(f{^\prime}))$
as the “local” variance (of
![]() $f{^\prime}$
at
$f{^\prime}$
at
![]() $x$
).
$x$
).
We will establish (12) using induction. Let
![]() $v$
be a vertex of degree
$v$
be a vertex of degree
![]() $1$
in
$1$
in
![]() $T{^\prime}$
and let
$T{^\prime}$
and let
![]() $u$
be the unique neighbour of
$u$
be the unique neighbour of
![]() $v$
. Let
$v$
. Let
![]() $T=(V,E)$
be the tree by removing
$T=(V,E)$
be the tree by removing
![]() $v$
from
$v$
from
![]() $T{^\prime}$
, i.e.,
$T{^\prime}$
, i.e.,
![]() $T$
is the induced subgraph of
$T$
is the induced subgraph of
![]() $T{^\prime}$
on
$T{^\prime}$
on
![]() $V=V{^\prime}\setminus \{v\}$
. Let
$V=V{^\prime}\setminus \{v\}$
. Let
![]() $\{\lambda _w\}_{w\in V}$
be a collection of fugacities where
$\{\lambda _w\}_{w\in V}$
be a collection of fugacities where
![]() $\lambda _w = \lambda ^{\prime}_w$
for
$\lambda _w = \lambda ^{\prime}_w$
for
![]() $w\neq u$
and
$w\neq u$
and
![]() $\lambda _u=\lambda ^{\prime}_u/(1+\lambda ^{\prime}_v)$
. Let
$\lambda _u=\lambda ^{\prime}_u/(1+\lambda ^{\prime}_v)$
. Let
![]() $\mu$
be the hard-core measure on
$\mu$
be the hard-core measure on
![]() $T$
with fugacities
$T$
with fugacities
![]() $\{\lambda _w\}_{w\in V}$
.
$\{\lambda _w\}_{w\in V}$
.
Note that for
![]() $S\subseteq V$
we have
$S\subseteq V$
we have
Fix a function
![]() $f{^\prime}\,:\,2^{V{^\prime}}\rightarrow{\mathbb{R}}$
. Let
$f{^\prime}\,:\,2^{V{^\prime}}\rightarrow{\mathbb{R}}$
. Let
![]() $f\,:\,2^V\rightarrow{\mathbb{R}}$
be defined by
$f\,:\,2^V\rightarrow{\mathbb{R}}$
be defined by
Note that
![]() $f{^\prime}$
is defined on independent sets of the tree
$f{^\prime}$
is defined on independent sets of the tree
![]() $T{^\prime}$
and
$T{^\prime}$
and
![]() $f$
is the natural projection of
$f$
is the natural projection of
![]() $f{^\prime}$
to the tree
$f{^\prime}$
to the tree
![]() $T$
. Since
$T$
. Since
![]() $f=\mu^{\prime}_v(f{^\prime})$
, then by Lemma 2.2 we have that:
$f=\mu^{\prime}_v(f{^\prime})$
, then by Lemma 2.2 we have that:
For measure
![]() $\mu^{\prime}$
, when we condition on the configuration at
$\mu^{\prime}$
, when we condition on the configuration at
![]() $u$
, the configuration at
$u$
, the configuration at
![]() $V\setminus \{u\}$
is independent of that at
$V\setminus \{u\}$
is independent of that at
![]() $\{v\}$
. Hence, from Equation (10) for any
$\{v\}$
. Hence, from Equation (10) for any
![]() $x\not \in \{u,v\}$
(by setting
$x\not \in \{u,v\}$
(by setting
![]() $U=\{x\}$
and
$U=\{x\}$
and
![]() $W=\{v\}$
) we have:
$W=\{v\}$
) we have:
Since by (13) we have
![]() $\mu (\mathrm{Var}_x(f))=\mu^{\prime}(\mathrm{Var}_x(f))$
, the above implies that
$\mu (\mathrm{Var}_x(f))=\mu^{\prime}(\mathrm{Var}_x(f))$
, the above implies that
The following lemma is the main technical ingredient. It bounds the local variance at
![]() $u$
for the smaller graph
$u$
for the smaller graph
![]() $T$
in terms of the local variance at
$T$
in terms of the local variance at
![]() $u$
and
$u$
and
![]() $v$
in the original graph
$v$
in the original graph
![]() $T{^\prime}$
.
$T{^\prime}$
.
Lemma 3.1.
For
![]() $F(x)=1000 (1+x)^2 \exp\!(1.3x)$
and any
$F(x)=1000 (1+x)^2 \exp\!(1.3x)$
and any
![]() $\lambda _v,\lambda _u\in (0,1.1]$
we have:
$\lambda _v,\lambda _u\in (0,1.1]$
we have:
We now utilise the above lemma to prove the main theorem for the relaxation time. We then go back to prove Lemma 3.1.
Proof of Theorem 1.1. Note Equation (17) is equivalent to:
We can prove variance tensorization by induction as follows:
 \begin{align*} \mathrm{Var}(f{^\prime}) &= \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + \mathrm{Var}(f) \\ &\leq \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + \sum _{x\in V} F(\lambda _x) \mu (\mathrm{Var}_x(f)) \\ & \leq \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + F(\lambda _u) \mu (\mathrm{Var}_u(f)) + \sum _{x\in V\setminus \{u\}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})) \\ & \le F(\lambda ^{\prime}_v)\mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + F(\lambda ^{\prime}_u) \mu^{\prime}(\mathrm{Var}_u(f{^\prime})) + \sum _{x\in V\setminus \{u\}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})) \\ & = \sum _{x\in V^{\prime}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})). \end{align*}
\begin{align*} \mathrm{Var}(f{^\prime}) &= \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + \mathrm{Var}(f) \\ &\leq \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + \sum _{x\in V} F(\lambda _x) \mu (\mathrm{Var}_x(f)) \\ & \leq \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + F(\lambda _u) \mu (\mathrm{Var}_u(f)) + \sum _{x\in V\setminus \{u\}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})) \\ & \le F(\lambda ^{\prime}_v)\mu^{\prime}(\mathrm{Var}_v(f{^\prime})) + F(\lambda ^{\prime}_u) \mu^{\prime}(\mathrm{Var}_u(f{^\prime})) + \sum _{x\in V\setminus \{u\}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})) \\ & = \sum _{x\in V^{\prime}} F(\lambda ^{\prime}_x) \mu^{\prime}(\mathrm{Var}_x(f{^\prime})). \end{align*}
For the first line, we use Equation (15). The second line follows from the inductive hypothesis. For the third line, we use Equation (16) and the fact that
![]() $F(\lambda _x)\leq F(\lambda ^{\prime}_x)$
, since
$F(\lambda _x)\leq F(\lambda ^{\prime}_x)$
, since
![]() $F$
is increasing and
$F$
is increasing and
![]() $\lambda _x\leq \lambda ^{\prime}_x$
. The fourth line follows by using Equation (18).
$\lambda _x\leq \lambda ^{\prime}_x$
. The fourth line follows by using Equation (18).
Our task now is to prove Lemma 3.1. The following technical inequality will be useful.
Lemma 3.2.
Let
![]() $p\in [0,1]$
. Suppose
$p\in [0,1]$
. Suppose
![]() $s_1,s_2\gt 0$
satisfy
$s_1,s_2\gt 0$
satisfy
![]() $s_1 s_2 \geq 1$
. Then for all
$s_1 s_2 \geq 1$
. Then for all
![]() $A,B,C\in{\mathbb{R}}$
we have
$A,B,C\in{\mathbb{R}}$
we have
Proof. Equation (19) is equivalent to
We derive the above by subtracting
![]() $(C-A)^2$
and
$(C-A)^2$
and
![]() $(1-p)^2(B-A)^2$
from both sides of equation (19) and rearranging.
$(1-p)^2(B-A)^2$
from both sides of equation (19) and rearranging.
A simple application of the AM-GM inequality implies that
Then, equation (20) follows from the observation that the left-hand side of the above inequality is at least
![]() $2(1-p)(C-A)(A-B)$
, i.e., since
$2(1-p)(C-A)(A-B)$
, i.e., since
![]() $s_1s_2\geq 1$
.
$s_1s_2\geq 1$
.
We can now prove the main lemma.
Proof of Lemma 3.1 . Our goal is to prove Eq. (17), let us recall its statement:
We will consider each of these local variances
![]() $\mu (\mathrm{Var}_u(f))$
,
$\mu (\mathrm{Var}_u(f))$
,
![]() $\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, and
$\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, and
![]() $\mu^{\prime}(\mathrm{Var}_u(f{^\prime}))$
. We will express each of them as a sum over independent sets
$\mu^{\prime}(\mathrm{Var}_u(f{^\prime}))$
. We will express each of them as a sum over independent sets
![]() $S$
of
$S$
of
![]() $V{^\prime}$
. We can then establish Eq. (17) in a pointwise manner by considering the corresponding inequality for each independent set
$V{^\prime}$
. We can then establish Eq. (17) in a pointwise manner by considering the corresponding inequality for each independent set
![]() $S$
.
$S$
.
Let us begin by looking at the general definition of the expected local variance
![]() $\mu^{\prime}(\mathrm{Var}_x(f{^\prime}))$
for any
$\mu^{\prime}(\mathrm{Var}_x(f{^\prime}))$
for any
![]() $x\in V{^\prime}$
. Applying the definition in Eq. (5) and then simplifying we obtain the following (a reader familar with the notation can apply Eq. (7) to skip directly to the last line):
$x\in V{^\prime}$
. Applying the definition in Eq. (5) and then simplifying we obtain the following (a reader familar with the notation can apply Eq. (7) to skip directly to the last line):
 \begin{align} \nonumber\!\!{\mu^{\prime}(\mathrm{Var}_x(f{^\prime})) } \\ &= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \mu^{\prime}_{V{^\prime} \setminus \{x\}}(S)\cdot \mathrm{Var}_x^S(f_S) \nonumber \\ &= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \left ( \sum _{T\subseteq \{x\}} \mu^{\prime}(S\cup T)\right ) \left ( \frac 12\sum _{T,U\subseteq \{x\}, T\neq U} \mu _{x}^{{^\prime}S}(T)\mu _x^{{^\prime}S}(U)(f{^\prime}(S\cup T)-f{^\prime}(S\cup U))^2\right )\!\! \nonumber \\&= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \left ( \sum _{T\subseteq \{x\}} \mu^{\prime}(S\cup T)\right ) \left ( \mu _{x}^{{^\prime}S}(x)\mu _x^{{^\prime}S}(\emptyset )(f{^\prime}(S)-f{^\prime}(S\cup \{x\}))^2\right )\! \nonumber \\ &= \sum _{S\subseteq V{^\prime}\setminus \{x\}} \Big (\mu^{\prime}(S)+\mu^{\prime}(S\cup \{x\})\Big ) \frac{\mu^{\prime}(S)\mu^{\prime}(S\cup \{x\})}{(\mu^{\prime}(S)+\mu^{\prime}(S\cup \{x\}))^2} \Big (f{^\prime}(S) - f{^\prime}(S\cup \{x\}) \Big )^2 . \end{align}
\begin{align} \nonumber\!\!{\mu^{\prime}(\mathrm{Var}_x(f{^\prime})) } \\ &= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \mu^{\prime}_{V{^\prime} \setminus \{x\}}(S)\cdot \mathrm{Var}_x^S(f_S) \nonumber \\ &= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \left ( \sum _{T\subseteq \{x\}} \mu^{\prime}(S\cup T)\right ) \left ( \frac 12\sum _{T,U\subseteq \{x\}, T\neq U} \mu _{x}^{{^\prime}S}(T)\mu _x^{{^\prime}S}(U)(f{^\prime}(S\cup T)-f{^\prime}(S\cup U))^2\right )\!\! \nonumber \\&= \sum _{S \subseteq V{^\prime} \setminus \{x\}} \left ( \sum _{T\subseteq \{x\}} \mu^{\prime}(S\cup T)\right ) \left ( \mu _{x}^{{^\prime}S}(x)\mu _x^{{^\prime}S}(\emptyset )(f{^\prime}(S)-f{^\prime}(S\cup \{x\}))^2\right )\! \nonumber \\ &= \sum _{S\subseteq V{^\prime}\setminus \{x\}} \Big (\mu^{\prime}(S)+\mu^{\prime}(S\cup \{x\})\Big ) \frac{\mu^{\prime}(S)\mu^{\prime}(S\cup \{x\})}{(\mu^{\prime}(S)+\mu^{\prime}(S\cup \{x\}))^2} \Big (f{^\prime}(S) - f{^\prime}(S\cup \{x\}) \Big )^2 . \end{align}
Notice in Eq. (21) that the only
![]() $S\subset V{^\prime}\setminus \{x\}$
which contribute are those where
$S\subset V{^\prime}\setminus \{x\}$
which contribute are those where
![]() $x$
is unblocked (i.e., no neighbour of
$x$
is unblocked (i.e., no neighbour of
![]() $x$
is included in the independent set
$x$
is included in the independent set
![]() $S$
) because we need that
$S$
) because we need that
![]() $S$
and
$S$
and
![]() $S\cup \{x\}$
are both independent sets and hence have positive measure in
$S\cup \{x\}$
are both independent sets and hence have positive measure in
![]() $\mu^{\prime}$
.
$\mu^{\prime}$
.
Let us now consider each of the local variances appearing in Eq. (17) (expressed using carefully chosen summations that will allow us to prove (17) term-by-term in terms of
![]() $S$
).
$S$
).
Let
![]() $Q_1\,:\!=\,\mu (\mathrm{Var}_u(f))$
denote the expected local variance of
$Q_1\,:\!=\,\mu (\mathrm{Var}_u(f))$
denote the expected local variance of
![]() $f$
at
$f$
at
![]() $u$
. We will use (21) (applied to
$u$
. We will use (21) (applied to
![]() $T$
instead of
$T$
instead of
![]() $T{^\prime}$
); note that only
$T{^\prime}$
); note that only
![]() $S$
where
$S$
where
![]() $u$
is unblocked (that is, when no neighbour of
$u$
is unblocked (that is, when no neighbour of
![]() $u$
is occupied) contribute to the local variance. Moreover, we can express the expected local variance of
$u$
is occupied) contribute to the local variance. Moreover, we can express the expected local variance of
![]() $f$
at
$f$
at
![]() $u$
in terms of only those
$u$
in terms of only those
![]() $S$
where
$S$
where
![]() $u\in S$
. In particular, consider an independent set
$u\in S$
. In particular, consider an independent set
![]() $S{^\prime}$
where
$S{^\prime}$
where
![]() $u\notin S{^\prime}$
. Note that if
$u\notin S{^\prime}$
. Note that if
![]() $u$
is blocked (i.e.,
$u$
is blocked (i.e.,
![]() $N(u)\cap S{^\prime}\neq \emptyset$
) then the local variance at
$N(u)\cap S{^\prime}\neq \emptyset$
) then the local variance at
![]() $u$
is zero for this term. And for those
$u$
is zero for this term. And for those
![]() $S{^\prime}$
where
$S{^\prime}$
where
![]() $u\notin S{^\prime}$
and
$u\notin S{^\prime}$
and
![]() $u$
is unblocked then the local variance has the same contribution as
$u$
is unblocked then the local variance has the same contribution as
![]() $S=S{^\prime}\cup \{u\}$
times
$S=S{^\prime}\cup \{u\}$
times
![]() $1/\lambda _u$
(since
$1/\lambda _u$
(since
![]() $\mu (S{^\prime}\cup \{u\})=\lambda _u \mu (S{^\prime})$
). Hence the expected local variance of
$\mu (S{^\prime}\cup \{u\})=\lambda _u \mu (S{^\prime})$
). Hence the expected local variance of
![]() $f$
at
$f$
at
![]() $u$
is given by
$u$
is given by
We have
![]() $f(S)=f{^\prime}(S)$
(since
$f(S)=f{^\prime}(S)$
(since
![]() $u\in S$
) and
$u\in S$
) and
![]() $f(S\setminus \{u\}) = \frac{1}{1+\lambda ^{\prime}_v} f{^\prime}(S\setminus \{u\}) - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} f{^\prime}(S\setminus \{u\}\cup \{v\})$
. Plugging these in and simplifying we obtain the following:
$f(S\setminus \{u\}) = \frac{1}{1+\lambda ^{\prime}_v} f{^\prime}(S\setminus \{u\}) - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} f{^\prime}(S\setminus \{u\}\cup \{v\})$
. Plugging these in and simplifying we obtain the following:
 \begin{equation} Q_1 = \frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v} \sum _{S\subseteq V; u\in S} \mu (S){\left (f{^\prime}(S)-\frac{1}{1+\lambda ^{\prime}_v} f{^\prime}(S-u) - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} f{^\prime}(S-u+v)\right )}^2. \end{equation}
\begin{equation} Q_1 = \frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v} \sum _{S\subseteq V; u\in S} \mu (S){\left (f{^\prime}(S)-\frac{1}{1+\lambda ^{\prime}_v} f{^\prime}(S-u) - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} f{^\prime}(S-u+v)\right )}^2. \end{equation}
We now consider
![]() $Q_2\,:\!=\,\mu^{\prime}(\mathrm{Var}_u(f{^\prime}))$
. As we did for
$Q_2\,:\!=\,\mu^{\prime}(\mathrm{Var}_u(f{^\prime}))$
. As we did for
![]() $Q_1$
we can express
$Q_1$
we can express
![]() $Q_2$
as a sum over indpendent sets
$Q_2$
as a sum over indpendent sets
![]() $S$
where
$S$
where
![]() $u\in S$
. In this case for an independent set
$u\in S$
. In this case for an independent set
![]() $S$
where
$S$
where
![]() $u\in S$
, consider
$u\in S$
, consider
![]() $S{^\prime}=S\setminus \{u\}$
and note that the following hold
$S{^\prime}=S\setminus \{u\}$
and note that the following hold
and
Hence, we have the following:
 \begin{align} \nonumber Q_2 \,:\!=\, \mu^{\prime}(\mathrm{Var}_u(f{^\prime})) & = \sum _{S\subseteq V; u\in S} \mu (S) \left (1+\frac{1}{\lambda ^{\prime}_u}\frac{1}{1+\lambda ^{\prime}_v}\right )\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_u}\frac{1}{1+\lambda ^{\prime}_u} \left (f{^\prime}(S-u)-f{^\prime}(S)\right )^2 \\ & = \left (\lambda ^{\prime}_u + \frac{1}{1+\lambda ^{\prime}_v} \right ) \frac{1}{(1+\lambda ^{\prime}_u)^2} \sum _{S\subseteq V; u\in S} \mu (S) \left (f{^\prime}(S)-f{^\prime}(S-u)\right )^2. \end{align}
\begin{align} \nonumber Q_2 \,:\!=\, \mu^{\prime}(\mathrm{Var}_u(f{^\prime})) & = \sum _{S\subseteq V; u\in S} \mu (S) \left (1+\frac{1}{\lambda ^{\prime}_u}\frac{1}{1+\lambda ^{\prime}_v}\right )\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_u}\frac{1}{1+\lambda ^{\prime}_u} \left (f{^\prime}(S-u)-f{^\prime}(S)\right )^2 \\ & = \left (\lambda ^{\prime}_u + \frac{1}{1+\lambda ^{\prime}_v} \right ) \frac{1}{(1+\lambda ^{\prime}_u)^2} \sum _{S\subseteq V; u\in S} \mu (S) \left (f{^\prime}(S)-f{^\prime}(S-u)\right )^2. \end{align}
Finally, we consider
![]() $\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, the expected local variance of
$\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, the expected local variance of
![]() $f{^\prime}$
at
$f{^\prime}$
at
![]() $v$
. We will establish a lower bound which we will denote by
$v$
. We will establish a lower bound which we will denote by
![]() $Q_3$
(note,
$Q_3$
(note,
![]() $Q_1$
and
$Q_1$
and
![]() $Q_2$
were identities but here we will have an inequality).
$Q_2$
were identities but here we will have an inequality).
To compute
![]() $\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, the expected local variance of
$\mu^{\prime}(\mathrm{Var}_v(f{^\prime}))$
, the expected local variance of
![]() $f{^\prime}$
at
$f{^\prime}$
at
![]() $v$
, we need to generate an independent set
$v$
, we need to generate an independent set
![]() $S{^\prime}$
from
$S{^\prime}$
from
![]() $\mu^{\prime}$
. Only those
$\mu^{\prime}$
. Only those
![]() $S{^\prime}$
where
$S{^\prime}$
where
![]() $v$
is unblocked (that is where
$v$
is unblocked (that is where
![]() $u$
is not in
$u$
is not in
![]() $S{^\prime}$
) contribute to the local variance. We can generate
$S{^\prime}$
) contribute to the local variance. We can generate
![]() $S{^\prime}$
by generating
$S{^\prime}$
by generating
![]() $S$
from
$S$
from
![]() $\mu$
(whether we add or do not add
$\mu$
(whether we add or do not add
![]() $v$
does not change the contribution to the local variance). As in Eq. (21), we obtain the following:
$v$
does not change the contribution to the local variance). As in Eq. (21), we obtain the following:
 \begin{align*} \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) & = \sum _{S{^\prime}\subseteq V; u\not \in S{^\prime}} \mu (S{^\prime}) \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S{^\prime}\cup \{v\})-f{^\prime}(S{^\prime})\right )^2 \\ & \geq \sum _{\substack{S{^\prime}\subseteq V; u\not \in S{^\prime}\\ \textrm{$u$ is unblocked}}} \mu (S{^\prime}) \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S{^\prime}\cup \{v\})-f{^\prime}(S{^\prime})\right )^2 \\ & = \sum _{S\subseteq V; u\in S} \mu (S) \frac{1}{\lambda ^{\prime}_u} \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S\cup \{v\}\setminus \{u\})-f{^\prime}(S\setminus \{u\})\right )^2. \end{align*}
\begin{align*} \mu^{\prime}(\mathrm{Var}_v(f{^\prime})) & = \sum _{S{^\prime}\subseteq V; u\not \in S{^\prime}} \mu (S{^\prime}) \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S{^\prime}\cup \{v\})-f{^\prime}(S{^\prime})\right )^2 \\ & \geq \sum _{\substack{S{^\prime}\subseteq V; u\not \in S{^\prime}\\ \textrm{$u$ is unblocked}}} \mu (S{^\prime}) \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S{^\prime}\cup \{v\})-f{^\prime}(S{^\prime})\right )^2 \\ & = \sum _{S\subseteq V; u\in S} \mu (S) \frac{1}{\lambda ^{\prime}_u} \frac{1}{1+\lambda ^{\prime}_v} \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v} \left (f{^\prime}(S\cup \{v\}\setminus \{u\})-f{^\prime}(S\setminus \{u\})\right )^2. \end{align*}
Let
![]() $Q_3$
denote the lower bound we obtained above:
$Q_3$
denote the lower bound we obtained above:
Plugging in (22), (23), (24) we obtain that Eq. (17) follows from the following inequality:
We will establish (25) term-by-term, that is, for each
![]() $S$
in the sums of (22), (23), (24). Fix
$S$
in the sums of (22), (23), (24). Fix
![]() $S\subseteq V$
such that
$S\subseteq V$
such that
![]() $u\in S$
and let
$u\in S$
and let
![]() $A=f{^\prime}(S-u)$
,
$A=f{^\prime}(S-u)$
,
![]() $B=f{^\prime}(S-u+v)$
, and
$B=f{^\prime}(S-u+v)$
, and
![]() $C=f{^\prime}(S)$
. We need to show
$C=f{^\prime}(S)$
. We need to show
 \begin{equation} \begin{split} \frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}\left (C -\frac{1}{1+\lambda ^{\prime}_v} A - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v}B \right ) ^2 F\left (\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right ) \hspace{1.5in} \\ \leq \frac{1 + \lambda ^{\prime}_v + \lambda ^{\prime}_u }{ 1+\lambda ^{\prime}_v } \frac{1}{(1+\lambda ^{\prime}_u)^2}\left (C-A\right )^2 F(\lambda ^{\prime}_u) + \frac{1}{\lambda ^{\prime}_u(1+\lambda ^{\prime}_v)^2}(B-A)^2\left (F(\lambda ^{\prime}_v) - 1\right ) . \end{split} \end{equation}
\begin{equation} \begin{split} \frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}\left (C -\frac{1}{1+\lambda ^{\prime}_v} A - \frac{\lambda ^{\prime}_v}{1+\lambda ^{\prime}_v}B \right ) ^2 F\left (\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right ) \hspace{1.5in} \\ \leq \frac{1 + \lambda ^{\prime}_v + \lambda ^{\prime}_u }{ 1+\lambda ^{\prime}_v } \frac{1}{(1+\lambda ^{\prime}_u)^2}\left (C-A\right )^2 F(\lambda ^{\prime}_u) + \frac{1}{\lambda ^{\prime}_u(1+\lambda ^{\prime}_v)^2}(B-A)^2\left (F(\lambda ^{\prime}_v) - 1\right ) . \end{split} \end{equation}
Let
![]() $p=1/(1+\lambda ^{\prime}_v)$
. We will match (19) to (26), by first dividing both sides of (26) by
$p=1/(1+\lambda ^{\prime}_v)$
. We will match (19) to (26), by first dividing both sides of (26) by
![]() $\frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}F\left (\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )$
and then choosing
$\frac{1+\lambda ^{\prime}_v}{1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}F\left (\frac{\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )$
and then choosing
 \begin{equation*} 1+s_1 = \left (\frac {1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}{(1+\lambda ^{\prime}_v)(1+\lambda ^{\prime}_u)}\right )^2 \cdot \frac {F(\lambda ^{\prime}_u)}{F\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )}\quad \mbox {and}\quad 1+s_2 = \frac {1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}{\lambda ^{\prime}_u(1+\lambda ^{\prime}_v){\lambda ^{\prime}_v}^2} \cdot \frac {F(\lambda ^{\prime}_v)-1}{F\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )} . \end{equation*}
\begin{equation*} 1+s_1 = \left (\frac {1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}{(1+\lambda ^{\prime}_v)(1+\lambda ^{\prime}_u)}\right )^2 \cdot \frac {F(\lambda ^{\prime}_u)}{F\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )}\quad \mbox {and}\quad 1+s_2 = \frac {1+\lambda ^{\prime}_u+\lambda ^{\prime}_v}{\lambda ^{\prime}_u(1+\lambda ^{\prime}_v){\lambda ^{\prime}_v}^2} \cdot \frac {F(\lambda ^{\prime}_v)-1}{F\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )} . \end{equation*}
Note that with this choice of
![]() $s_1$
and
$s_1$
and
![]() $s_2$
equations (19) and (26) are equivalent, and hence to prove (26) it is enough to show
$s_2$
equations (19) and (26) are equivalent, and hence to prove (26) it is enough to show
![]() $s_1 s_2\geq 1$
.
$s_1 s_2\geq 1$
.
Claim 3.3.
![]() $s_1s_2\geq 1.$
$s_1s_2\geq 1.$
This completes the proof of the lemma.
We use the following lemma to prove Claim 3.3
Lemma 3.4.
Let
![]() $\alpha =1.1$
and
$\alpha =1.1$
and
![]() $\beta =1.3$
. Suppose
$\beta =1.3$
. Suppose
![]() $x,y\in (0,\alpha ]$
are such that
$x,y\in (0,\alpha ]$
are such that
![]() $(1+x)y\in [0,\alpha ]$
. Then
$(1+x)y\in [0,\alpha ]$
. Then
Proof.
We will show that for
![]() $x,y,(1+x)y\in (0,\alpha ]$
we have
$x,y,(1+x)y\in (0,\alpha ]$
we have
and
To see that (28) and (29) imply (27) note
where the first inequality follows from (28) and the second from (29).
Note that the constraints on
![]() $x,y$
imply that
$x,y$
imply that
![]() $y+xy\leq \alpha$
and
$y+xy\leq \alpha$
and
![]() $xy\leq \alpha y$
. Hence
$xy\leq \alpha y$
. Hence
![]() $xy \leq \alpha /(1+1/\alpha )$
. To prove (29) it is sufficient to show for
$xy \leq \alpha /(1+1/\alpha )$
. To prove (29) it is sufficient to show for
![]() $z\in [0,\alpha /(1+1/\alpha )]$
$z\in [0,\alpha /(1+1/\alpha )]$
We have
Hence
![]() $\left (\exp\! (\beta z) - 1\right )\left (1.15 - z \right ) - 1.1 z$
is concave and we only need to check (30) for the endpoints of the interval; for
$\left (\exp\! (\beta z) - 1\right )\left (1.15 - z \right ) - 1.1 z$
is concave and we only need to check (30) for the endpoints of the interval; for
![]() $z=0$
LHS of (30) is zero, for
$z=0$
LHS of (30) is zero, for
![]() $z=\alpha /(1+1/\alpha )$
the LHS of (30) has value larger than
$z=\alpha /(1+1/\alpha )$
the LHS of (30) has value larger than
![]() $0.005$
. This concludes the proof of (29).
$0.005$
. This concludes the proof of (29).
To prove (28) note that
Hence we only need to prove (28) for
![]() $y=\alpha /(1+x)$
; this simplifies to showing
$y=\alpha /(1+x)$
; this simplifies to showing
For
![]() $x=0$
and
$x=0$
and
![]() $x=1.1$
we have that (32) is satisfied (using interval arithmetic). Let
$x=1.1$
we have that (32) is satisfied (using interval arithmetic). Let
The critical points of
![]() $Q(x)$
are roots of
$Q(x)$
are roots of
Since this polynomial is increasing when
![]() $x$
is non-negative, it has exactly one positive real root, which is in the interval
$x$
is non-negative, it has exactly one positive real root, which is in the interval
![]() $[0.30765554,0.30765555]$
. The value of
$[0.30765554,0.30765555]$
. The value of
![]() $Q(x)$
on both endpoints of the interval is at least
$Q(x)$
on both endpoints of the interval is at least
![]() $0.0032$
. The derivative of
$0.0032$
. The derivative of
![]() $Q(x)$
(a rational function) is bounded in absolute value by
$Q(x)$
(a rational function) is bounded in absolute value by
![]() $1$
on the interval and hence
$1$
on the interval and hence
![]() $Q(x)\gt 0$
on the entire interval (in particular at the critical point). This proves (32).
$Q(x)\gt 0$
on the entire interval (in particular at the critical point). This proves (32).
We can now complete the proof of Claim 3.3.
Proof of Claim 3.3
. We will use the following substitution to simplify the expression
![]() $F(x)=(1+x)^2 H(x)$
. Note that
$F(x)=(1+x)^2 H(x)$
. Note that
![]() $H(x)=1000\exp\! (1.3x)=1000\exp\! (\beta x)$
. In terms of
$H(x)=1000\exp\! (1.3x)=1000\exp\! (\beta x)$
. In terms of
![]() $H(x)$
we have
$H(x)$
we have
 \begin{equation*} 1+s_1 = \frac {H(\lambda ^{\prime}_u)}{H\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )}\quad \mbox {and}\quad 1+s_2 = \frac {1+\lambda ^{\prime}_v}{(1+\lambda ^{\prime}_u+\lambda ^{\prime}_v)\lambda ^{\prime}_u}\cdot \frac {(1+\lambda ^{\prime}_v)^2 H(\lambda ^{\prime}_v) - 1}{H\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )} . \end{equation*}
\begin{equation*} 1+s_1 = \frac {H(\lambda ^{\prime}_u)}{H\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )}\quad \mbox {and}\quad 1+s_2 = \frac {1+\lambda ^{\prime}_v}{(1+\lambda ^{\prime}_u+\lambda ^{\prime}_v)\lambda ^{\prime}_u}\cdot \frac {(1+\lambda ^{\prime}_v)^2 H(\lambda ^{\prime}_v) - 1}{H\left (\frac {\lambda ^{\prime}_u}{1+\lambda ^{\prime}_v}\right )} . \end{equation*}
Let
![]() $\lambda ^{\prime}_v=x$
and
$\lambda ^{\prime}_v=x$
and
![]() $\lambda ^{\prime}_u=y(1+x)$
. We have
$\lambda ^{\prime}_u=y(1+x)$
. We have
Recall, our goal is to show
![]() $s_1s_2\geq 1$
. First we show that for
$s_1s_2\geq 1$
. First we show that for
![]() $x,y\in (0,1.1]$
such that
$x,y\in (0,1.1]$
such that
![]() $(1+x)y\leq 1.1$
we have
$(1+x)y\leq 1.1$
we have
Note that (33) is equivalent to
Note that the RHS of (34) is increasing in
![]() $y$
and hence it is sufficient to show (34) for the maximal value of
$y$
and hence it is sufficient to show (34) for the maximal value of
![]() $y=1.1/(1+x)$
; this is equivalent to
$y=1.1/(1+x)$
; this is equivalent to
the last inequality follows from
checked using Sturm sequences. This concludes the proof of (33).
Note that Lemma 3.4 is equivalent to the following
and hence
which combined with (33) yields
![]() $s_1 s_2\geq 1.1(999/1000) \gt 1$
, concluding the proof.
$s_1 s_2\geq 1.1(999/1000) \gt 1$
, concluding the proof.
4. Spectral independence for trees
Let
![]() $G=(V,E)$
be a graph. Suppose we have a set of fugacities
$G=(V,E)$
be a graph. Suppose we have a set of fugacities
![]() $\lambda _i$
for each
$\lambda _i$
for each
![]() $i\in V$
, and consider the corresponding Gibbs distribution. Recall that the influence matrix
$i\in V$
, and consider the corresponding Gibbs distribution. Recall that the influence matrix
![]() ${\mathcal{I}}_G$
has
${\mathcal{I}}_G$
has
![]() $u,v$
entry
$u,v$
entry
![]() ${\mbox{Inf}}(u\rightarrow v)$
, where
${\mbox{Inf}}(u\rightarrow v)$
, where
Let
![]() $u,v$
be any two vertices in a graph. We have
$u,v$
be any two vertices in a graph. We have
We have
Let
![]() $D$
be diagonal matrix with entries
$D$
be diagonal matrix with entries
![]() $\mu (v\in I)\mu (v\not \in I)$
. Equation (36) means that
$\mu (v\in I)\mu (v\not \in I)$
. Equation (36) means that
![]() $D{\mathcal{I}}_G$
is symmetric. That also means that
$D{\mathcal{I}}_G$
is symmetric. That also means that
![]() $D^{1/2}{\mathcal{I}}_G D^{-1/2}$
is symmetric (since it is obtained from
$D^{1/2}{\mathcal{I}}_G D^{-1/2}$
is symmetric (since it is obtained from
![]() $D{\mathcal{I}}_G$
by multiplying by the same diagonal matrix on the left and on the right). The
$D{\mathcal{I}}_G$
by multiplying by the same diagonal matrix on the left and on the right). The
![]() $u,v$
entry in
$u,v$
entry in
![]() $D^{1/2}{\mathcal{I}}_G D^{-1/2}$
is
$D^{1/2}{\mathcal{I}}_G D^{-1/2}$
is
which is equal to
![]() $\pm \sqrt{{\mbox{Inf}}(u\rightarrow v){\mbox{Inf}}(v\rightarrow u)}$
(take geometric mean of the sides of (37)). We will call
$\pm \sqrt{{\mbox{Inf}}(u\rightarrow v){\mbox{Inf}}(v\rightarrow u)}$
(take geometric mean of the sides of (37)). We will call
![]() $M = D^{1/2}{\mathcal{I}}_G D^{-1/2}$
the symmetrised influence matrix (since it is similar to the influence matrix, it has the same spectral radius).
$M = D^{1/2}{\mathcal{I}}_G D^{-1/2}$
the symmetrised influence matrix (since it is similar to the influence matrix, it has the same spectral radius).
We will prove the following result.
Lemma 4.1.
For any forest
![]() $T$
with fugacities in
$T$
with fugacities in
![]() $ [0,1.3]$
the spectral radius of the influence matrix of the hard-core model on
$ [0,1.3]$
the spectral radius of the influence matrix of the hard-core model on
![]() $T$
is bounded by 10000.
$T$
is bounded by 10000.
We will prove Lemma 4.1 by induction; we will prove the following strengthened statement.
Lemma 4.2.
For any forest
![]() $T$
with fugacities in
$T$
with fugacities in
![]() $[0,1.3]$
the symmetrised influence matrix
$[0,1.3]$
the symmetrised influence matrix
![]() $M$
of the hard-core model on
$M$
of the hard-core model on
![]() $T$
satisfies
$T$
satisfies
Proof.
Let
![]() $T=(V,E)$
be a forest. Let
$T=(V,E)$
be a forest. Let
![]() $v$
be a vertex of degree
$v$
be a vertex of degree
![]() $1$
in
$1$
in
![]() $T$
. Let
$T$
. Let
![]() $u$
be the neighbour of
$u$
be the neighbour of
![]() $v$
in
$v$
in
![]() $T$
. Let
$T$
. Let
![]() $T{^\prime}=(V{^\prime},E{^\prime})$
be
$T{^\prime}=(V{^\prime},E{^\prime})$
be
![]() $T$
with
$T$
with
![]() $v$
removed. Let
$v$
removed. Let
![]() $\lambda ^{\prime}_i = \lambda _i$
for
$\lambda ^{\prime}_i = \lambda _i$
for
![]() $i\in V{^\prime}\setminus \{u\}$
. Let
$i\in V{^\prime}\setminus \{u\}$
. Let
![]() $\lambda ^{\prime}_u = \lambda _u / (1+\lambda _v)$
. Let
$\lambda ^{\prime}_u = \lambda _u / (1+\lambda _v)$
. Let
![]() $\mu^{\prime}$
be the hard-core model on
$\mu^{\prime}$
be the hard-core model on
![]() $T{^\prime}$
with fugacities
$T{^\prime}$
with fugacities
![]() $\{\lambda ^{\prime}_i\}_{i\in V{^\prime}}$
. Note that
$\{\lambda ^{\prime}_i\}_{i\in V{^\prime}}$
. Note that
![]() $\mu^{\prime}$
is the same as the marginalisation of
$\mu^{\prime}$
is the same as the marginalisation of
![]() $\mu$
to
$\mu$
to
![]() $V{^\prime}$
, that is, for an independent set
$V{^\prime}$
, that is, for an independent set
![]() $I$
of
$I$
of
![]() $T{^\prime}$
we have
$T{^\prime}$
we have
where
![]() $J$
ranges over independent sets of
$J$
ranges over independent sets of
![]() $T$
that contain
$T$
that contain
![]() $I$
.
$I$
.
Let
![]() $M$
be the symmetrised influence matrix for
$M$
be the symmetrised influence matrix for
![]() $\mu$
and let
$\mu$
and let
![]() $M{^\prime}$
be the symmetrised influence matrix for
$M{^\prime}$
be the symmetrised influence matrix for
![]() $\mu^{\prime}$
. Note that (38) implies that
$\mu^{\prime}$
. Note that (38) implies that
![]() $M{^\prime}$
is a submatrix of
$M{^\prime}$
is a submatrix of
![]() $M$
(removing the column and row of
$M$
(removing the column and row of
![]() $M$
corresponding to vertex
$M$
corresponding to vertex
![]() $v$
yields
$v$
yields
![]() $M{^\prime}$
).
$M{^\prime}$
).
It is standard to show, e.g., see [[Reference Anari, Liu and Gharan1], Lemma B.3], that
and
Let
![]() $\tau ^2={\mbox{Inf}}(v\rightarrow u){\mbox{Inf}}(u\rightarrow v)$
. Note that, using (35), we have
$\tau ^2={\mbox{Inf}}(v\rightarrow u){\mbox{Inf}}(u\rightarrow v)$
. Note that, using (35), we have
From (39) and (40) we have that
![]() $M$
and
$M$
and
![]() $M{^\prime}$
have the following form (
$M{^\prime}$
have the following form (
![]() $Q$
is a matrix and
$Q$
is a matrix and
![]() $z$
is a vector):
$z$
is a vector):
 \begin{equation*} M{^\prime}=\left ( \begin {array}{c@{\quad}c} Q & z \\ z^T & 0 \\ \end {array} \right ) \quad \mbox {and}\quad M =\left ( \begin {array}{c@{\quad}c@{\quad}c} Q & z & \tau z \\ z^T & 0 & \tau \\ \tau z^T & \tau & 0 \\ \end {array} \right ) . \end{equation*}
\begin{equation*} M{^\prime}=\left ( \begin {array}{c@{\quad}c} Q & z \\ z^T & 0 \\ \end {array} \right ) \quad \mbox {and}\quad M =\left ( \begin {array}{c@{\quad}c@{\quad}c} Q & z & \tau z \\ z^T & 0 & \tau \\ \tau z^T & \tau & 0 \\ \end {array} \right ) . \end{equation*}
Let
![]() $F$
be an increasing function on
$F$
be an increasing function on
![]() $[0,1.3]$
. We will take
$[0,1.3]$
. We will take
![]() $F(x)=1/H(x)$
where
$F(x)=1/H(x)$
where
![]() $H(x)=(a-x^b)/400$
and
$H(x)=(a-x^b)/400$
and
![]() $a=1.3$
,
$a=1.3$
,
![]() $b=0.78$
. (We will keep
$b=0.78$
. (We will keep
![]() $a$
and
$a$
and
![]() $b$
as variables to elucidate the choice of
$b$
as variables to elucidate the choice of
![]() $a$
and
$a$
and
![]() $b$
in the proof below.) Suppose that we know
$b$
in the proof below.) Suppose that we know
![]() $M{^\prime} \preceq{\mathrm{diag}}(F(\lambda ^{\prime}_i))$
and we want to conclude
$M{^\prime} \preceq{\mathrm{diag}}(F(\lambda ^{\prime}_i))$
and we want to conclude
![]() $M\preceq{\mathrm{diag}}(F(\lambda _i))$
. Let
$M\preceq{\mathrm{diag}}(F(\lambda _i))$
. Let
![]() $W$
be a diagonal matrix with entries
$W$
be a diagonal matrix with entries
![]() $F(\lambda _i)$
for
$F(\lambda _i)$
for
![]() $i\in V\setminus \{u,v\}$
. We can restate our goal as follows.
$i\in V\setminus \{u,v\}$
. We can restate our goal as follows.
 \begin{equation*} \mbox {KNOW:}\left ( \begin {array}{c@{\quad}c@{\quad}} W - Q & -z \\ -z^T & F\Big (\frac {\lambda _u}{1+\lambda _v}\Big ) \\ \end {array} \right )\succeq 0 \quad \quad \mbox {WANT:}\left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}} W - Q & -z & -\tau z \\ -z^T & F(\lambda _u) & -\tau \\ -\tau z^T & -\tau & F(\lambda _v) \\ \end {array} \right )\succeq 0 . \end{equation*}
\begin{equation*} \mbox {KNOW:}\left ( \begin {array}{c@{\quad}c@{\quad}} W - Q & -z \\ -z^T & F\Big (\frac {\lambda _u}{1+\lambda _v}\Big ) \\ \end {array} \right )\succeq 0 \quad \quad \mbox {WANT:}\left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}} W - Q & -z & -\tau z \\ -z^T & F(\lambda _u) & -\tau \\ -\tau z^T & -\tau & F(\lambda _v) \\ \end {array} \right )\succeq 0 . \end{equation*}
Since
![]() $F$
will be an increasing function, we have
$F$
will be an increasing function, we have
![]() $F(\lambda _u / (1+\lambda _v))\lt F(\lambda _u)$
.
$F(\lambda _u / (1+\lambda _v))\lt F(\lambda _u)$
.
The condition we want is equivalent (by applying row and column operations, specifically subtracting
![]() $u$
-th row/column times
$u$
-th row/column times
![]() $\tau$
from the
$\tau$
from the
![]() $v$
-th row/column) to
$v$
-th row/column) to
 \begin{equation*}\left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}} W - Q & -z & 0 \\ -z^T & F(\lambda _u) & -\tau (1+F(\lambda _u)) \\ 0 & -\tau (1+F(\lambda _u)) & F(\lambda _v) + 2\tau ^2 + \tau ^2 F(\lambda _u)\\ \end {array} \right )\succeq 0 . \end{equation*}
\begin{equation*}\left ( \begin {array}{c@{\quad}c@{\quad}c@{\quad}} W - Q & -z & 0 \\ -z^T & F(\lambda _u) & -\tau (1+F(\lambda _u)) \\ 0 & -\tau (1+F(\lambda _u)) & F(\lambda _v) + 2\tau ^2 + \tau ^2 F(\lambda _u)\\ \end {array} \right )\succeq 0 . \end{equation*}
If we show
 \begin{equation} \left ( \begin{array}{c@{\quad}c@{\quad}} F(\lambda _u) - F(\lambda _u / (1+\lambda _v)) & -\tau (1+F(\lambda _u)) \\ -\tau (1+F(\lambda _u)) & F(\lambda _v) + 2\tau ^2 + \tau ^2 F(\lambda _u) \\ \end{array} \right )\succeq 0, \end{equation}
\begin{equation} \left ( \begin{array}{c@{\quad}c@{\quad}} F(\lambda _u) - F(\lambda _u / (1+\lambda _v)) & -\tau (1+F(\lambda _u)) \\ -\tau (1+F(\lambda _u)) & F(\lambda _v) + 2\tau ^2 + \tau ^2 F(\lambda _u) \\ \end{array} \right )\succeq 0, \end{equation}
then the conclusion will follow (adding the “know” positive semidefinite matrix and (42) (expanded with zeros to match dimensions) yields that the “want” matrix is positive semidefinite). Equation (42) is equivalent to checking if the determinant is positive (since the entry in the first row/column is positive), that is, we need to check
Hence it is sufficient (using (41)) to show
Letting
![]() $H(x)=1/F(x)$
the condition becomes the following
$H(x)=1/F(x)$
the condition becomes the following
We are going to search for
![]() $H$
that is 1) bounded from above by
$H$
that is 1) bounded from above by
![]() $1/300$
, 2) bounded away from
$1/300$
, 2) bounded away from
![]() $0$
on
$0$
on
![]() $[0,1.3]$
and 3) that satisfies
$[0,1.3]$
and 3) that satisfies
Note that such
![]() $H$
will also satisfy (43) since
$H$
will also satisfy (43) since
![]() $H\Big (\frac{\lambda _u}{1+\lambda _v}\Big )H(\lambda _u) + 2H(\lambda _u)\leq 1/100$
(here the choice of
$H\Big (\frac{\lambda _u}{1+\lambda _v}\Big )H(\lambda _u) + 2H(\lambda _u)\leq 1/100$
(here the choice of
![]() $1/100$
is arbitrary; we just need something sufficiently small).
$1/100$
is arbitrary; we just need something sufficiently small).
We will search for
![]() $H$
of the following form:
$H$
of the following form:
![]() $H(x) \propto a - x^b$
. Note that (44) is invariant under scaling of
$H(x) \propto a - x^b$
. Note that (44) is invariant under scaling of
![]() $H$
and hence satisfying the upper bound of
$H$
and hence satisfying the upper bound of
![]() $1/300$
can be achieved by scaling of
$1/300$
can be achieved by scaling of
![]() $H$
. Ultimately the price we will pay for
$H$
. Ultimately the price we will pay for
![]() $H$
being small is that
$H$
being small is that
![]() $F$
is big and hence we get a weaker upper bound on the spectral radius of
$F$
is big and hence we get a weaker upper bound on the spectral radius of
![]() $M$
; we do not optimise the constants at this point. Consider the following function
$M$
; we do not optimise the constants at this point. Consider the following function
![]() $L$
(obtained as LHS of (44) divided by RHS of (44), excluding the constant term
$L$
(obtained as LHS of (44) divided by RHS of (44), excluding the constant term
![]() $1+1/100$
):
$1+1/100$
):
The minimum of the first term in (45) is attained for
![]() $\lambda _u=(1-b)/b$
and hence setting
$\lambda _u=(1-b)/b$
and hence setting
![]() $b=.78$
we have that:
$b=.78$
we have that:
For the second term in (45) by setting
![]() $a=1.3$
we have the following:
$a=1.3$
we have the following:
The second inequality in (47) is obtained from the following inequality which is valid for
![]() $b\in [0,1]$
and
$b\in [0,1]$
and
![]() $x\geq 0$
:
$x\geq 0$
:
For the above, it suffices to prove that
We have that for
![]() $b\leq 1$
:
$b\leq 1$
:
 \begin{align*} (1+x)^{b} - b x (1+x)^{b-1}&=(1+x)^{b-1}(1 - (b-1)x) \\ &\geq (1+x)^{b-1}(1+x)^{-(b-1)} & \mbox{by Bernoulli's inequality} \\ & \geq 1. \end{align*}
\begin{align*} (1+x)^{b} - b x (1+x)^{b-1}&=(1+x)^{b-1}(1 - (b-1)x) \\ &\geq (1+x)^{b-1}(1+x)^{-(b-1)} & \mbox{by Bernoulli's inequality} \\ & \geq 1. \end{align*}
Finally, plugging in (46) and (47) into (45) we obtain:
Equation (50) implies that (44) is satisfied. Recall that the statement of the lemma assumed that the fugacities are in the interval
![]() $[0,1.3]$
. For
$[0,1.3]$
. For
![]() $\lambda \in [0,1.3]$
we have
$\lambda \in [0,1.3]$
we have
This implies that
![]() $H$
satisfies (43) and hence for
$H$
satisfies (43) and hence for
we have (42) and this completes the proof of Lemma 4.2 by induction.
We can now complete the proof for spectral independence.
Proof of Theorem 1.2
. We apply Theorem 1.12 of [Reference Chen, Liu and Vigoda16] which says that if for all pinnings we have
![]() $\eta$
-spectral independence and
$\eta$
-spectral independence and
![]() $b$
-marginally boundedness then the mixing time of the Glauber dynamics is
$b$
-marginally boundedness then the mixing time of the Glauber dynamics is
![]() $C(\eta, \Delta, b)n\log{n}$
. A pinning refers to a fixed configuration
$C(\eta, \Delta, b)n\log{n}$
. A pinning refers to a fixed configuration
![]() $\tau$
on a subset
$\tau$
on a subset
![]() $S$
of vertices; for the hard-core model a pinning of a tree
$S$
of vertices; for the hard-core model a pinning of a tree
![]() $T$
corresponds to the hard-core model on a forest which is an induced subgraph. Hence, Lemma 4.1 implies that
$T$
corresponds to the hard-core model on a forest which is an induced subgraph. Hence, Lemma 4.1 implies that
![]() $\eta$
-spectral independence holds for all pinnings with
$\eta$
-spectral independence holds for all pinnings with
![]() $\eta =10000$
. The condition
$\eta =10000$
. The condition
![]() $b$
-marginally boundedness (see Definition 1.9 in [Reference Chen, Liu and Vigoda16]) says that for every pinning
$b$
-marginally boundedness (see Definition 1.9 in [Reference Chen, Liu and Vigoda16]) says that for every pinning
![]() $\tau$
on a subset
$\tau$
on a subset
![]() $S\subset V$
, for every vertex
$S\subset V$
, for every vertex
![]() $v\notin S$
, for every assignment to
$v\notin S$
, for every assignment to
![]() $v$
denoted as
$v$
denoted as
![]() $\sigma (v)$
which has positive probability in the conditional Gibbs distribution
$\sigma (v)$
which has positive probability in the conditional Gibbs distribution
![]() $\mu _\tau$
, then the marginal probability is lower bounded as
$\mu _\tau$
, then the marginal probability is lower bounded as
![]() $\mu _\tau (\sigma (v))\geq b$
. This holds for
$\mu _\tau (\sigma (v))\geq b$
. This holds for
![]() $b\geq \min \{1,\lambda \}/[\lambda +(1+\lambda )^\Delta ]$
. Hence, [[Reference Chen, Liu and Vigoda16], Theorem 1.12] implies Theorem1.2.
$b\geq \min \{1,\lambda \}/[\lambda +(1+\lambda )^\Delta ]$
. Hence, [[Reference Chen, Liu and Vigoda16], Theorem 1.12] implies Theorem1.2.
5. Proof of Corollary 1.3
We prove Corollary 1.3 by combining the spectral independence result in Lemma 4.1 and Theorem1.1, while we utilise [[Reference Chen, Feng, Yin and Zhang13], Theorem 1.9].
In [Reference Chen, Feng, Yin and Zhang13], they introduce the notion of “complete
![]() $\eta$
-spectral independence”. Let
$\eta$
-spectral independence”. Let
![]() $\mu$
be the hard-core model on graph
$\mu$
be the hard-core model on graph
![]() $G=(V,E)$
with fugacity
$G=(V,E)$
with fugacity
![]() $\lambda$
. For
$\lambda$
. For
![]() $\eta \gt 0$
, complete
$\eta \gt 0$
, complete
![]() $\eta$
-spectral independence for
$\eta$
-spectral independence for
![]() $\mu$
corresponds to the following condition: For any induced subgraph
$\mu$
corresponds to the following condition: For any induced subgraph
![]() $G{^\prime}$
of
$G{^\prime}$
of
![]() $G$
, for the hard-core model
$G$
, for the hard-core model
![]() $\mu^{\prime}$
on
$\mu^{\prime}$
on
![]() $G{^\prime}$
such that each vertex
$G{^\prime}$
such that each vertex
![]() $v\in V$
has fugacity
$v\in V$
has fugacity
![]() $\lambda ^{\prime}_v\leq \lambda$
, the corresponding influence matrix
$\lambda ^{\prime}_v\leq \lambda$
, the corresponding influence matrix
![]() $\mathcal{I}_{G{^\prime}}$
has spectral radius at most
$\mathcal{I}_{G{^\prime}}$
has spectral radius at most
![]() $\eta$
.
$\eta$
.
Lemma 4.1 is equivalent to complete
![]() $\eta$
-spectral independence for all
$\eta$
-spectral independence for all
![]() $\lambda \leq 1.3$
with
$\lambda \leq 1.3$
with
![]() $\eta \leq 10000$
. We can now prove Corollary 1.3.
$\eta \leq 10000$
. We can now prove Corollary 1.3.
Proof of Corollary
1.3. For the forest
![]() $T$
, let
$T$
, let
![]() $\mu$
be the hard-core model with fugacity
$\mu$
be the hard-core model with fugacity
![]() $\lambda \leq 1.3$
. Also, let
$\lambda \leq 1.3$
. Also, let
![]() $\gamma$
be the spectral gap for Glauber dynamics on
$\gamma$
be the spectral gap for Glauber dynamics on
![]() $\mu$
. Corollary 1.3 follows by showing that
$\mu$
. Corollary 1.3 follows by showing that
![]() $\gamma =\Omega (n^{-1})$
.
$\gamma =\Omega (n^{-1})$
.
First, note that if
![]() $\lambda \lt 1.1$
, then Theorem1.1 already implies
$\lambda \lt 1.1$
, then Theorem1.1 already implies
![]() $\gamma =\Omega (n^{-1})$
. We now focus on the case where
$\gamma =\Omega (n^{-1})$
. We now focus on the case where
![]() $\lambda \in [1.1,1.3]$
.
$\lambda \in [1.1,1.3]$
.
For the same forest
![]() $T$
, let
$T$
, let
![]() $\widehat{\mu }$
be the hard-core model on
$\widehat{\mu }$
be the hard-core model on
![]() $T$
with fugacity
$T$
with fugacity
![]() $\widehat{\lambda }=1$
. Let
$\widehat{\lambda }=1$
. Let
![]() $\widehat{\gamma }$
be the spectral gap for Glauber dynamics on
$\widehat{\gamma }$
be the spectral gap for Glauber dynamics on
![]() $\widehat{\mu }$
. From Theorem1.1, we have that
$\widehat{\mu }$
. From Theorem1.1, we have that
Lemma 4.1 and [[Reference Chen, Yang, Yin and Zhang9], Theorem 1.9] imply the following relation between
![]() $\gamma$
and
$\gamma$
and
![]() $\widehat{\gamma }$
: for
$\widehat{\gamma }$
: for
![]() $\theta =\lambda$
and
$\theta =\lambda$
and
![]() $\eta \leq 10000$
, we have
$\eta \leq 10000$
, we have
From (52) and (53), we get that
![]() $\gamma =\Omega (n^{-1})$
, for any
$\gamma =\Omega (n^{-1})$
, for any
![]() $\lambda \in [1.1,1.3]$
.
$\lambda \in [1.1,1.3]$
.
From the above we have established Corollary 1.3.