Article contents
On Universal Threshold Graphs
Published online by Cambridge University Press: 12 September 2008
Abstract
A graph G is threshold if there exists a ‘weight’ function w: V(G) → R such that the total weight of any stable set of G is less than the total weight of any non-stable set of G. Let 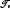 n denote the set of threshold graphs with n vertices. A graph is called
n denote the set of threshold graphs with n vertices. A graph is called 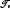 n-universal if it contains every threshold graph with n vertices as an induced subgraph.
n-universal if it contains every threshold graph with n vertices as an induced subgraph. 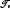 n-universal threshold graphs are of special interest, since they are precisely those
n-universal threshold graphs are of special interest, since they are precisely those 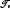 n-universal graphs that do not contain any non-threshold induced subgraph.
n-universal graphs that do not contain any non-threshold induced subgraph.
In this paper we shall study minimum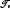 n-universal (threshold) graphs, i.e.
n-universal (threshold) graphs, i.e.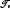 n-universal (threshold) graphs having the minimum number of vertices.
n-universal (threshold) graphs having the minimum number of vertices.
It is shown that for any n ≥ 3 there exist minimum 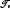 n-universal graphs, which are themselves threshold, and others which are not.
n-universal graphs, which are themselves threshold, and others which are not.
Two extremal minimum 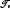 n-universal graphs having respectively the minimum and the maximum number of edges are described, it is proved that they are unique, and that they are threshold graphs.
n-universal graphs having respectively the minimum and the maximum number of edges are described, it is proved that they are unique, and that they are threshold graphs.
The set of all minimum 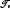 n-universal threshold graphs is then described constructively; it is shown that it forms a lattice isomorphic to the n − 1 dimensional Boolean cube, and that the minimum and the maximum elements of this lattice are the two extremal graphs introduced above.
n-universal threshold graphs is then described constructively; it is shown that it forms a lattice isomorphic to the n − 1 dimensional Boolean cube, and that the minimum and the maximum elements of this lattice are the two extremal graphs introduced above.
The proofs provide a (polynomial) recursive procedure that determines for any threshold graph G with n vertices and for any minimum 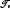 n-universal threshold graph T, an induced subgraph G' of T isomorphic to G.
n-universal threshold graph T, an induced subgraph G' of T isomorphic to G.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1994
References
- 9
- Cited by


