No CrossRef data available.
Published online by Cambridge University Press: 28 November 2022
We prove new mixing rate estimates for the random walks on homogeneous spaces determined by a probability distribution on a finite group
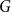 $G$
. We introduce the switched random walk determined by a finite set of probability distributions on
$G$
. We introduce the switched random walk determined by a finite set of probability distributions on
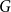 $G$
, prove that its long-term behaviour is determined by the Fourier joint spectral radius of the distributions, and give Hermitian sum-of-squares algorithms for the effective estimation of this quantity.
$G$
, prove that its long-term behaviour is determined by the Fourier joint spectral radius of the distributions, and give Hermitian sum-of-squares algorithms for the effective estimation of this quantity.