Article contents
The Infinite limit of random permutations avoiding patterns of length three
Published online by Cambridge University Press: 14 October 2019
Abstract
For 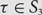 $$\tau \in {S_3}$$, let
$$\tau \in {S_3}$$, let 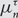 $$\mu _n^\tau $$ denote the uniformly random probability measure on the set of
$$\mu _n^\tau $$ denote the uniformly random probability measure on the set of  $$\tau $$-avoiding permutations in
$$\tau $$-avoiding permutations in 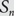 $${S_n}$$. Let
$${S_n}$$. Let 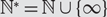 $${\mathbb {N}^*} = {\mathbb {N}} \cup \{ \infty \} $$ with an appropriate metric and denote by
$${\mathbb {N}^*} = {\mathbb {N}} \cup \{ \infty \} $$ with an appropriate metric and denote by 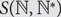 $$S({\mathbb{N}},{\mathbb{N}^*})$$ the compact metric space consisting of functions
$$S({\mathbb{N}},{\mathbb{N}^*})$$ the compact metric space consisting of functions 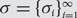 $$\sigma {\rm{ = }}\{ {\sigma _i}\} _{i = 1}^\infty {\rm{ }}$$ from
$$\sigma {\rm{ = }}\{ {\sigma _i}\} _{i = 1}^\infty {\rm{ }}$$ from 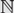 $$\mathbb {N}$$ to
$$\mathbb {N}$$ to 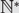 $${\mathbb {N}^ * }$$ which are injections when restricted to
$${\mathbb {N}^ * }$$ which are injections when restricted to 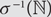 $${\sigma ^{ - 1}}(\mathbb {N})$$; that is, if
$${\sigma ^{ - 1}}(\mathbb {N})$$; that is, if 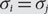 $${\sigma _i}{\rm{ = }}{\sigma _j}$$,
$${\sigma _i}{\rm{ = }}{\sigma _j}$$, 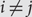 $$i \ne j$$, then
$$i \ne j$$, then  $${\sigma _i} = \infty $$. Extending permutations
$${\sigma _i} = \infty $$. Extending permutations 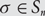 $$\sigma \in {S_n}$$ by defining
$$\sigma \in {S_n}$$ by defining  $${\sigma _j} = j$$, for
$${\sigma _j} = j$$, for 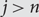 $$j \gt n$$, we have
$$j \gt n$$, we have 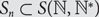 $${S_n} \subset S({\mathbb{N}},{{\mathbb{N}}^*})$$. For each
$${S_n} \subset S({\mathbb{N}},{{\mathbb{N}}^*})$$. For each 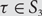 $$\tau \in {S_3}$$, we study the limiting behaviour of the measures
$$\tau \in {S_3}$$, we study the limiting behaviour of the measures 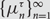 $$\{ \mu _n^\tau \} _{n = 1}^\infty $$ on
$$\{ \mu _n^\tau \} _{n = 1}^\infty $$ on 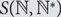 $$S({\mathbb{N}},{\mathbb{N}^*})$$. We obtain partial results for the permutation
$$S({\mathbb{N}},{\mathbb{N}^*})$$. We obtain partial results for the permutation 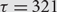 $$\tau = 321$$ and complete results for the other five permutations
$$\tau = 321$$ and complete results for the other five permutations 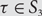 $$\tau \in {S_3}$$.
$$\tau \in {S_3}$$.
MSC classification
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
References
- 2
- Cited by


