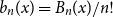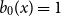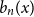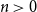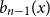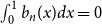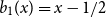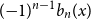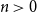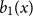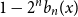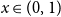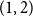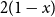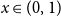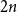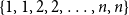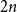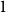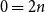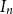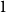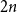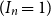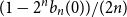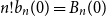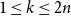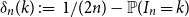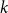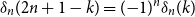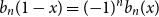1. Introduction
The Bernoulli polynomials
![]() $(B_n(x))_{n \geq 0}$
are a special sequence of univariate polynomials with rational coefficients. They are named after the Swiss mathematician Jakob Bernoulli (1654–1705), who (in his Ars Conjectandi published posthumously in Basel 1713) found the sum of
$(B_n(x))_{n \geq 0}$
are a special sequence of univariate polynomials with rational coefficients. They are named after the Swiss mathematician Jakob Bernoulli (1654–1705), who (in his Ars Conjectandi published posthumously in Basel 1713) found the sum of
![]() $m$
th powers of the first
$m$
th powers of the first
![]() $n$
positive integers using the instance
$n$
positive integers using the instance
![]() $x = 1$
of the power sum formula
$x = 1$
of the power sum formula
 \begin{equation} \sum _{k=0}^{n-1} (x+k)^{m} = \frac{ B_{m+1} (x+n) - B_{m+1}(x) }{ m + 1}, \qquad (n = 1,2, \ldots, m = 0,1,2, \ldots ) . \end{equation}
\begin{equation} \sum _{k=0}^{n-1} (x+k)^{m} = \frac{ B_{m+1} (x+n) - B_{m+1}(x) }{ m + 1}, \qquad (n = 1,2, \ldots, m = 0,1,2, \ldots ) . \end{equation}
The evaluations
![]() $B_m\,:\!=\, B_m(0)$
and
$B_m\,:\!=\, B_m(0)$
and
![]() $B_m(1) = ({-}1)^{m} B_m$
are known as the Bernoulli numbers, from which the polynomials are recovered as
$B_m(1) = ({-}1)^{m} B_m$
are known as the Bernoulli numbers, from which the polynomials are recovered as
These polynomials have been well studied, starting from the early work of Faulhaber, Bernoulli, Seki and Euler in the
![]() $17$
th and early
$17$
th and early
![]() $18$
th centuries. They can be defined in multiple ways. For example, Euler defined the Bernoulli polynomials by their exponential generating function
$18$
th centuries. They can be defined in multiple ways. For example, Euler defined the Bernoulli polynomials by their exponential generating function
Beyond evaluating power sums, the Bernoulli numbers and polynomials are useful in other contexts and appear in many areas in mathematics, among which we mention number theory [Reference Agoh1, Reference Arakawa, Ibukiyama and Kaneko2, Reference Ayoub4, Reference Mazur28], Lie theory [Reference Bourbaki6, Reference Buijs, Carrasquel-Vera and Murillo7, Reference Magnus27, Reference Romik36], algebraic geometry and topology [Reference Hirzebruch and Schwarzenberger17, Reference Milnor and Kervaire29], probability [Reference Biane, Pitman and Yor5, Reference Ikeda and Taniguchi19, Reference Ikeda and Taniguchi20, Reference Lévy25, Reference Lévy26, Reference Pitman and Yor34, Reference Sun39] and numerical approximation [Reference Phillips33, Reference Steffensen38].
The factorially normalised Bernoulli polynomials
![]() $b_n(x)\,:\!=\, B_n(x)/n!$
can also be defined inductively as follows (see [Reference Montgomery30, §9.5]). Beginning with
$b_n(x)\,:\!=\, B_n(x)/n!$
can also be defined inductively as follows (see [Reference Montgomery30, §9.5]). Beginning with
![]() $b_0(x) = B_0(x) = 1$
, for each positive integer
$b_0(x) = B_0(x) = 1$
, for each positive integer
![]() $n$
, the function
$n$
, the function
![]() $x \mapsto b_n(x)$
is the unique anti-derivative of
$x \mapsto b_n(x)$
is the unique anti-derivative of
![]() $x \mapsto b_{n-1}(x)$
that integrates to
$x \mapsto b_{n-1}(x)$
that integrates to
![]() $0$
over
$0$
over
![]() $[0,1]$
:
$[0,1]$
:
So the first few polynomials
![]() $b_n(x)$
are
$b_n(x)$
are
 \begin{align*} b_0(x) &= 1, &b_1(x) &= x - 1/2,\\[3pt] b_2(x) &= \frac{1}{2!}(x^2 - x - 1/6), &b_3(x) &= \frac{1}{3!}(x^3 - 3 x^2/2 + x/2). \end{align*}
\begin{align*} b_0(x) &= 1, &b_1(x) &= x - 1/2,\\[3pt] b_2(x) &= \frac{1}{2!}(x^2 - x - 1/6), &b_3(x) &= \frac{1}{3!}(x^3 - 3 x^2/2 + x/2). \end{align*}
As shown in [Reference Montgomery30, Theorem 9.7] starting from (1.4), the functions
![]() $f(x) = b_n(x)$
with argument
$f(x) = b_n(x)$
with argument
![]() $x \in [0,1)$
are also characterised by the simple form of their Fourier transform
$x \in [0,1)$
are also characterised by the simple form of their Fourier transform
which is given by
 \begin{equation} \begin{alignedat}{2} \widehat{b}_0(k) &= 1[ k = 0], \qquad &\mbox{for } k \in \mathbb{Z} ; \\[3pt] \widehat{b}_n(0) &= 0 \quad \text{and} \quad \widehat{b}_n(k) = - \frac{1}{(2 \pi i k)^n}, \qquad &\mbox{for } n \gt 0 \mbox{ and } k \ne 0, \end{alignedat} \end{equation}
\begin{equation} \begin{alignedat}{2} \widehat{b}_0(k) &= 1[ k = 0], \qquad &\mbox{for } k \in \mathbb{Z} ; \\[3pt] \widehat{b}_n(0) &= 0 \quad \text{and} \quad \widehat{b}_n(k) = - \frac{1}{(2 \pi i k)^n}, \qquad &\mbox{for } n \gt 0 \mbox{ and } k \ne 0, \end{alignedat} \end{equation}
with the notation
![]() $1[\dots ]$
equal to
$1[\dots ]$
equal to
![]() $1$
if
$1$
if
![]() $[\dots ]$
holds and
$[\dots ]$
holds and
![]() $0$
otherwise. It follows from the Fourier expansion of
$0$
otherwise. It follows from the Fourier expansion of
![]() $b_{n}(x)$
:
$b_{n}(x)$
:
 \begin{equation*} b_n(x) = - \frac {2}{(2\pi )^n} \sum _{k = 1}^{\infty } \frac {1}{k^n} \cos \left (2k\pi x - \frac {n\pi }{2}\right ) \end{equation*}
\begin{equation*} b_n(x) = - \frac {2}{(2\pi )^n} \sum _{k = 1}^{\infty } \frac {1}{k^n} \cos \left (2k\pi x - \frac {n\pi }{2}\right ) \end{equation*}
that there exists a constant
![]() $C \gt 0$
such that
$C \gt 0$
such that
see [Reference Lehmer22]. So as
![]() $n \uparrow \infty$
the polynomials
$n \uparrow \infty$
the polynomials
![]() $b_n(x)$
looks like shifted cosine functions. Besides (1.3) and (1.4), several other characterisations of the Bernoulli polynomials are described in [Reference Costabile, Dell’Accio and Gualtieri10, Reference Lehmer23].
$b_n(x)$
looks like shifted cosine functions. Besides (1.3) and (1.4), several other characterisations of the Bernoulli polynomials are described in [Reference Costabile, Dell’Accio and Gualtieri10, Reference Lehmer23].
This article first draws attention to a simple characterisation of the Bernoulli polynomials by circular convolution and, more importantly, provides an interesting probabilistic and combinatorial interpretation in terms of statistics of random permutations of a multiset.
For a pair of functions
![]() $f = f(u)$
and
$f = f(u)$
and
![]() $g = g(u)$
, defined for
$g = g(u)$
, defined for
![]() $u$
in
$u$
in
![]() $[0,1)$
identified with the circle group
$[0,1)$
identified with the circle group
![]() ${\mathbb{T}}\,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$
, with
${\mathbb{T}}\,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$
, with
![]() $f$
and
$f$
and
![]() $g$
integrable with respect to Lebesgue measure on
$g$
integrable with respect to Lebesgue measure on
![]() $\mathbb{T}$
, their circular convolution
$\mathbb{T}$
, their circular convolution
![]() $f\circledast g$
is the function
$f\circledast g$
is the function
Here
![]() $u-v$
is evaluated in the circle group
$u-v$
is evaluated in the circle group
![]() $\mathbb{T}$
, that is modulo
$\mathbb{T}$
, that is modulo
![]() $1$
, and
$1$
, and
![]() $dv$
is the shift-invariant Lebesgue measure on
$dv$
is the shift-invariant Lebesgue measure on
![]() $\mathbb{T}$
with total measure
$\mathbb{T}$
with total measure
![]() $1$
. Iteration of this operation defines the
$1$
. Iteration of this operation defines the
![]() $n$
th convolution power
$n$
th convolution power
![]() $u \mapsto f^{\circledast n}(u)$
for each positive integer
$u \mapsto f^{\circledast n}(u)$
for each positive integer
![]() $n$
, each integrable
$n$
, each integrable
![]() $f$
, and
$f$
, and
![]() $u \in{\mathbb{T}}$
.
$u \in{\mathbb{T}}$
.
Theorem 1.1.
The factorially normalised Bernoulli polynomials
![]() $b_n(x) = \frac{B_n(x)}{n!}$
are characterised by:
$b_n(x) = \frac{B_n(x)}{n!}$
are characterised by:
-
1.
 $b_0(x) = 1$
and
$b_0(x) = 1$
and
 $b_1(x) = x - 1/2$
,
$b_1(x) = x - 1/2$
, -
2. for
 $n \gt 0$
the
$n \gt 0$
the
 $n$
-fold circular convolution of
$n$
-fold circular convolution of
 $b_1(x)$
with itself is
$b_1(x)$
with itself is
 $({-}1)^{n-1} b_n(x)$
; that is
(1.9)
$({-}1)^{n-1} b_n(x)$
; that is
(1.9) \begin{equation} b_n(x) = ({-}1)^{n-1} b_1^{\circledast n}(x). \end{equation}
\begin{equation} b_n(x) = ({-}1)^{n-1} b_1^{\circledast n}(x). \end{equation}
In view of the identity
![]() $\widehat{f \circledast g} = \widehat{f} \ \widehat{g}$
, Theorem 1.1 follows from the classical Fourier evaluation (1.6) and uniqueness of the Fourier transform. A more elementary proof of Theorem 1.1, without Fourier transforms, is provided in Section 2. So the Fourier evaluation (1.6) may be regarded as a corollary of Theorem 1.1. That theorem can also be reformulated as follows:
$\widehat{f \circledast g} = \widehat{f} \ \widehat{g}$
, Theorem 1.1 follows from the classical Fourier evaluation (1.6) and uniqueness of the Fourier transform. A more elementary proof of Theorem 1.1, without Fourier transforms, is provided in Section 2. So the Fourier evaluation (1.6) may be regarded as a corollary of Theorem 1.1. That theorem can also be reformulated as follows:
Corollary 1.2. The following identities hold for circular convolution of factorially normalised Bernoulli polynomials:
 \begin{align*} b_0(x) \circledast b_0(x) &= b_0(x)\\[3pt] b_0(x) \circledast b_n(x) &= 0, \quad (n \geq 1),\\[3pt] b_n(x) \circledast b_m(x) &= - b_{n + m}(x), \quad (n, m \geq 1).\\[3pt] \end{align*}
\begin{align*} b_0(x) \circledast b_0(x) &= b_0(x)\\[3pt] b_0(x) \circledast b_n(x) &= 0, \quad (n \geq 1),\\[3pt] b_n(x) \circledast b_m(x) &= - b_{n + m}(x), \quad (n, m \geq 1).\\[3pt] \end{align*}
In particular, for positive integers
![]() $n$
and
$n$
and
![]() $m$
, this evaluation of
$m$
, this evaluation of
![]() $(b_n \circledast b_m)(1)$
yields an identity which appears in [Reference Nörlund32, p. 31]:
$(b_n \circledast b_m)(1)$
yields an identity which appears in [Reference Nörlund32, p. 31]:
Here the first equality is due to the well-known reflection symmetry of the Bernoulli polynomials
which is the identity of coefficients of
![]() $\lambda ^m$
in the elementary identity of Eulerian generating functions
$\lambda ^m$
in the elementary identity of Eulerian generating functions
The rest of this article is organised as follows. Section 2 gives an elementary proof for Theorem 1.1, and discusses circular convolution of polynomials. In Section 3 we highlight the fact that
![]() $1 - 2^n b_n(x)$
is the probability density at
$1 - 2^n b_n(x)$
is the probability density at
![]() $x \in (0,1)$
of the fractional part of a sum of
$x \in (0,1)$
of the fractional part of a sum of
![]() $n$
independent random variables, each with the beta
$n$
independent random variables, each with the beta
![]() $(1,2)$
probability density
$(1,2)$
probability density
![]() $2(1-x)$
at
$2(1-x)$
at
![]() $x \in (0,1)$
. Because the minimum of two independent uniform
$x \in (0,1)$
. Because the minimum of two independent uniform
![]() $[0,1]$
variables has this beta
$[0,1]$
variables has this beta
![]() $(1,2)$
probability density the circular convolution of
$(1,2)$
probability density the circular convolution of
![]() $n$
independent beta
$n$
independent beta
![]() $(1,2)$
variables is closely related to a continuous model we call the Bernoulli clock: Spray the circle
$(1,2)$
variables is closely related to a continuous model we call the Bernoulli clock: Spray the circle
![]() ${\mathbb{T}} = [0,1)$
of circumference
${\mathbb{T}} = [0,1)$
of circumference
![]() $1$
with
$1$
with
![]() $2n$
i.i.d uniform positions
$2n$
i.i.d uniform positions
![]() $U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$
with order statistics
$U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$
with order statistics
Starting from the origin
![]() $0$
, move clockwise to the first of position of the pair
$0$
, move clockwise to the first of position of the pair
![]() $(U_1, U^{\prime}_1)$
, continue clockwise to the first position of the pair
$(U_1, U^{\prime}_1)$
, continue clockwise to the first position of the pair
![]() $(U_2, U^{\prime}_2)$
, and so on, continuing clockwise around the circle until the first of the two positions
$(U_2, U^{\prime}_2)$
, and so on, continuing clockwise around the circle until the first of the two positions
![]() $(U_n,U^{\prime}_n)$
is encountered at a random index
$(U_n,U^{\prime}_n)$
is encountered at a random index
![]() $1 \leq I_n \leq 2n$
(i.e. we stop at
$1 \leq I_n \leq 2n$
(i.e. we stop at
![]() $U_{I_n:2n}$
) after having made a random number
$U_{I_n:2n}$
) after having made a random number
![]() $0 \leq D_n \leq n - 1$
turns around the circle. Then for each positive integer
$0 \leq D_n \leq n - 1$
turns around the circle. Then for each positive integer
![]() $n$
, the event
$n$
, the event
![]() $( I_n = 1)$
has probability
$( I_n = 1)$
has probability
where
![]() $n! b_n(0) = B_n(0)$
is the
$n! b_n(0) = B_n(0)$
is the
![]() $n$
th Bernoulli number. For
$n$
th Bernoulli number. For
![]() $ 1 \le k \le 2 n$
, the difference
$ 1 \le k \le 2 n$
, the difference
is a polynomial function of
![]() $k$
, which is closely related to
$k$
, which is closely related to
![]() $b_n(x)$
. In particular, this difference has the surprising symmetry
$b_n(x)$
. In particular, this difference has the surprising symmetry
which is a combinatorial analogue of the reflection symmetry (1.11) for the Bernoulli polynomials.
Stripping down the clock model, the random variables
![]() $I_n$
and
$I_n$
and
![]() $D_n$
are two statistics of permutations of the multiset
$D_n$
are two statistics of permutations of the multiset
Section 4 discusses the combinatorics behind the distributions of
![]() $I_n$
and
$I_n$
and
![]() $D_n$
. In Section 5 we generalise the Bernoulli clock model to offer a new perspective on the work of Horton and Kurn [Reference Horton and Kurn18] and the more recent work of Clifton et al [Reference Clifton, Deb, Huang, Spiro and Yoo8]. In particular, we provide a probabilistic interpretation for the permutation counting problem in [Reference Horton and Kurn18] and prove Conjectures 4.1 and 4.2 of [Reference Clifton, Deb, Huang, Spiro and Yoo8]. Moreover, we explicitly compute the mean function on
$D_n$
. In Section 5 we generalise the Bernoulli clock model to offer a new perspective on the work of Horton and Kurn [Reference Horton and Kurn18] and the more recent work of Clifton et al [Reference Clifton, Deb, Huang, Spiro and Yoo8]. In particular, we provide a probabilistic interpretation for the permutation counting problem in [Reference Horton and Kurn18] and prove Conjectures 4.1 and 4.2 of [Reference Clifton, Deb, Huang, Spiro and Yoo8]. Moreover, we explicitly compute the mean function on
![]() $[0,1]$
of a renewal process with i.i.d. beta(
$[0,1]$
of a renewal process with i.i.d. beta(
![]() $1,m$
)-jumps. The expression of this mean function is given in terms of the complex roots of the exponential polynomial
$1,m$
)-jumps. The expression of this mean function is given in terms of the complex roots of the exponential polynomial
![]() $E_m(x) \,:\!=\, 1 + x/1! + \dots + x^m/m!$
, and its derivatives at
$E_m(x) \,:\!=\, 1 + x/1! + \dots + x^m/m!$
, and its derivatives at
![]() $0$
are precisely the moments of these roots, as studied in [Reference Zemyan40].
$0$
are precisely the moments of these roots, as studied in [Reference Zemyan40].
The circular convolution identities for Bernoulli polynomials are closely related to the decomposition of a realvalued random variable -
![]() $X$
into its integer part
$X$
into its integer part
![]() $\lfloor X \rfloor \in \mathbb{Z}$
and its fractional part
$\lfloor X \rfloor \in \mathbb{Z}$
and its fractional part
![]() $ X^\circ \in{\mathbb{T}} \,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$
:
$ X^\circ \in{\mathbb{T}} \,:\!=\,{\mathbb{R}}/\mathbb{Z} = [0,1)$
:
If
![]() $\gamma _{1}$
is a random variable with standard exponential distribution, then for each positive real
$\gamma _{1}$
is a random variable with standard exponential distribution, then for each positive real
![]() $\lambda$
we have the expansion
$\lambda$
we have the expansion
 \begin{equation} \frac{d}{du}{\mathbb{P}}( (\gamma _1/\lambda )^\circ \le u ) = \frac{\lambda e^{- \lambda u } }{ 1 - e^{-\lambda } } = B(u,-\lambda ) = \sum _{n \ge 0} b_n(u) ({-}\lambda )^n . \end{equation}
\begin{equation} \frac{d}{du}{\mathbb{P}}( (\gamma _1/\lambda )^\circ \le u ) = \frac{\lambda e^{- \lambda u } }{ 1 - e^{-\lambda } } = B(u,-\lambda ) = \sum _{n \ge 0} b_n(u) ({-}\lambda )^n . \end{equation}
Here the first two equations hold for all real
![]() $\lambda \ne 0$
and
$\lambda \ne 0$
and
![]() $u \in [0,1)$
, but the final equality holds with a convergent power series only for
$u \in [0,1)$
, but the final equality holds with a convergent power series only for
![]() $0 \lt |\lambda | \lt 2 \pi$
. Section 6 presents a generalisation of formula (1.15) with the standard exponential variable
$0 \lt |\lambda | \lt 2 \pi$
. Section 6 presents a generalisation of formula (1.15) with the standard exponential variable
![]() $\gamma _1$
replaced by the gamma distributed sum
$\gamma _1$
replaced by the gamma distributed sum
![]() $\gamma _r$
of
$\gamma _r$
of
![]() $r$
independent copies of
$r$
independent copies of
![]() $\gamma _1$
, for a positive integer
$\gamma _1$
, for a positive integer
![]() $r$
. This provides an elementary probabilistic interpretation and proof of a formula due to Erdélyi, Magnus, Oberhettinger, and Tricomi [Reference Erdélyi, Magnus, Oberhettinger and Tricomi15, Section 1.11, page 30] relating the Hurwitz-Lerch zeta function (first studied in [Reference Lerch24])
$r$
. This provides an elementary probabilistic interpretation and proof of a formula due to Erdélyi, Magnus, Oberhettinger, and Tricomi [Reference Erdélyi, Magnus, Oberhettinger and Tricomi15, Section 1.11, page 30] relating the Hurwitz-Lerch zeta function (first studied in [Reference Lerch24])
to Bernoulli polynomials. Moreover, the expansion (6.4) in Proposition 6.1 quantifies how the distribution of the fractional part of a
![]() $\gamma _{r,\lambda }$
random variable approaches the uniform distribution on the circle in terms of Bernoulli polynomials, where the latter are viewed as signed measures on the circle.
$\gamma _{r,\lambda }$
random variable approaches the uniform distribution on the circle in terms of Bernoulli polynomials, where the latter are viewed as signed measures on the circle.
2. Circular convolution of polynomials
Theorem 1.1 follows easily by induction on
![]() $n$
from the characterisation (1.4) of the Bernoulli polynomials, and the action of circular convolution by the function
$n$
from the characterisation (1.4) of the Bernoulli polynomials, and the action of circular convolution by the function
as described by the following lemma.
Lemma 2.1.
For each Riemann integrable function
![]() $f$
with domain
$f$
with domain
![]() $[0,1)$
, the circular convolution
$[0,1)$
, the circular convolution
![]() $h = f \circledast ({-}b_1)$
is continuous on
$h = f \circledast ({-}b_1)$
is continuous on
![]() $\mathbb{T}$
, implying
$\mathbb{T}$
, implying
![]() $h(0) = h(1{-})$
. Moreover,
$h(0) = h(1{-})$
. Moreover,
and at each
![]() $u \in (0,1)$
at which
$u \in (0,1)$
at which
![]() $f$
is continuous,
$f$
is continuous,
![]() $h$
is differentiable with
$h$
is differentiable with
In particular, if
![]() $f$
is bounded and continuous on
$f$
is bounded and continuous on
![]() $(0,1)$
, then
$(0,1)$
, then
![]() $h = f \circledast ({-}b_1)$
is the unique continuous function
$h = f \circledast ({-}b_1)$
is the unique continuous function
![]() $h$
on
$h$
on
![]() $\mathbb{T}$
subject to (
2.2
) with derivative (
2.3
) at every
$\mathbb{T}$
subject to (
2.2
) with derivative (
2.3
) at every
![]() $u \in (0,1)$
.
$u \in (0,1)$
.
Proof. According to the definition of circular convolution (1.8),
In particular, for
![]() $g(u) = - b_1(u)$
, and a generic integrable function
$g(u) = - b_1(u)$
, and a generic integrable function
![]() $f$
,
$f$
,
 \begin{align*} ( f \circledast ({-}b_1) )(u) &= \int _0^u f(v) ( v - u + 1/2) dv + \int _u^1 f(v) ( v - u - 1/2) dv \\[3pt] &= \frac{1}{2} \left [ \int _0^u f(v) d v - \int _u ^1 f(v) dv \right ] - u \int _0^1 f(v) dv + \int _0^1 v f(v) dv. \end{align*}
\begin{align*} ( f \circledast ({-}b_1) )(u) &= \int _0^u f(v) ( v - u + 1/2) dv + \int _u^1 f(v) ( v - u - 1/2) dv \\[3pt] &= \frac{1}{2} \left [ \int _0^u f(v) d v - \int _u ^1 f(v) dv \right ] - u \int _0^1 f(v) dv + \int _0^1 v f(v) dv. \end{align*}
Differentiate this identity with respect to
![]() $u$
, to see that
$u$
, to see that
![]() $h \,:\!=\, f \circledast ({-}b_1)$
has the derivative displayed in (2.3) at every
$h \,:\!=\, f \circledast ({-}b_1)$
has the derivative displayed in (2.3) at every
![]() $u \in (0,1)$
at which
$u \in (0,1)$
at which
![]() $f$
is continuous, by the fundamental theorem of calculus. Also, this identity shows
$f$
is continuous, by the fundamental theorem of calculus. Also, this identity shows
![]() $h$
is continuous on
$h$
is continuous on
![]() $(0,1)$
with
$(0,1)$
with
![]() $h(0) = h(0{+}) = h(1{-})$
, hence
$h(0) = h(0{+}) = h(1{-})$
, hence
![]() $h$
is continous with respect to the topology of the circle
$h$
is continous with respect to the topology of the circle
![]() $\mathbb{T}$
. This
$\mathbb{T}$
. This
![]() $h$
has integral
$h$
has integral
![]() $0$
by associativity of circular convolution:
$0$
by associativity of circular convolution:
![]() $h \circledast 1 = f \circledast ({-}b_1) \circledast 1 = f \circledast 0 = 0$
. Assuming further that
$h \circledast 1 = f \circledast ({-}b_1) \circledast 1 = f \circledast 0 = 0$
. Assuming further that
![]() $f$
is bounded and continuous on
$f$
is bounded and continuous on
![]() $(0,1)$
, the uniqueness of
$(0,1)$
, the uniqueness of
![]() $h$
is obvious.
$h$
is obvious.
The reformulation of Theorem 1.1 in Corollary 1.2 displays how simple it is to convolve Bernoulli polynomials on the circle. On the other hand, convolving monomials is less pleasant, as the following calculations show.
Lemma 2.2.
For real parameters
![]() $n \gt 0$
and
$n \gt 0$
and
![]() $m \gt - 1$
,
$m \gt - 1$
,
Proof. Integrate by parts to obtain
 \begin{align*}{x^n} \circledast{x^m} &= \int _{0}^{x} u^{n} (x - u)^m du + \int _{x}^{1} u^{n} (1 + x - u)^m du \\[3pt] &= \frac{n}{m+1}\int _{0}^{x} u^{n-1} (x - u)^{m+1} du + \frac{n}{m+1} \int _{x}^{1} u^{n-1} (1 + x - u)^m du + \frac{x^n - x^{m+1}}{m+1} \end{align*}
\begin{align*}{x^n} \circledast{x^m} &= \int _{0}^{x} u^{n} (x - u)^m du + \int _{x}^{1} u^{n} (1 + x - u)^m du \\[3pt] &= \frac{n}{m+1}\int _{0}^{x} u^{n-1} (x - u)^{m+1} du + \frac{n}{m+1} \int _{x}^{1} u^{n-1} (1 + x - u)^m du + \frac{x^n - x^{m+1}}{m+1} \end{align*}
and hence (2.4).
Proposition 2.3 (Convolving monomials). For each positive integer
![]() $n$
$n$
and for all positive integers
![]() $m$
and
$m$
and
![]() $n$
$n$
 \begin{equation} {x^m} \circledast{x^n} ={x^n} \circledast{x^m} = \frac{n! \ m!}{(n+m+1)!} + \sum _{k = 0}^{n-1} \frac{n!}{ (n-k)! (m+1)_{k+1}} ({x}^{n-k} -{x}^{m+k+1}) \end{equation}
\begin{equation} {x^m} \circledast{x^n} ={x^n} \circledast{x^m} = \frac{n! \ m!}{(n+m+1)!} + \sum _{k = 0}^{n-1} \frac{n!}{ (n-k)! (m+1)_{k+1}} ({x}^{n-k} -{x}^{m+k+1}) \end{equation}
and with the Pochhammer notation
![]() $(m+1)_{k+1} \,:\!=\, (m+1) \dots (m+k+1)$
. In particular
$(m+1)_{k+1} \,:\!=\, (m+1) \dots (m+k+1)$
. In particular
Proof. By induction, using Lemma 2.2.
Remark 2.4.
-
1. By inspection of (2.6) the polynomial
 $\left ({x^n} \circledast{x^m} - \frac{n! \ m!}{(n+m+1)!}\right )/ x$
is an anti-reciprocal polynomial with rational coefficients.
$\left ({x^n} \circledast{x^m} - \frac{n! \ m!}{(n+m+1)!}\right )/ x$
is an anti-reciprocal polynomial with rational coefficients. -
2. Theorem 1.1 can be proved by inductive application of Proposition 2.3 to the expansion of the Bernoulli polynomials
 $B_n(x)$
in the monomial basis. This argument is unnecessarily complicated, but boils down to two following identities for the Bernoulli numbers
$B_n(x)$
in the monomial basis. This argument is unnecessarily complicated, but boils down to two following identities for the Bernoulli numbers
 $B_n\,:\!=\, B_n(0)$
for
$B_n\,:\!=\, B_n(0)$
for
 $n \geq 1$
:(2.7)
$n \geq 1$
:(2.7) \begin{equation} B_{n} = \frac{-1}{n + 1} \sum _{k = 0}^{n-1} \binom{n+1}{k} B_{k} \end{equation}
(2.8)The identity (2.7) is a commonly used recursion for the Bernoulli numbers. We do not know any reference for (2.8), but this can be checked by manipulation of Euler’s generating function (1.3). We refer the reader to Section A for more details.
\begin{equation} B_{n} = \frac{-1}{n + 1} \sum _{k = 0}^{n-1} \binom{n+1}{k} B_{k} \end{equation}
(2.8)The identity (2.7) is a commonly used recursion for the Bernoulli numbers. We do not know any reference for (2.8), but this can be checked by manipulation of Euler’s generating function (1.3). We refer the reader to Section A for more details. \begin{equation}\frac{B_{n+1}}{(n+1)!} = - \sum _{k = 0}^{n} \frac{1}{(k+2)!} \frac{B_{n-k}}{(n-k)!}. \end{equation}
\begin{equation}\frac{B_{n+1}}{(n+1)!} = - \sum _{k = 0}^{n} \frac{1}{(k+2)!} \frac{B_{n-k}}{(n-k)!}. \end{equation}
-
3. Using the hypergeometric function
 $F \,:\!=\,{}_{2}{F}_1$
, it follows from Equation (2.6) that:
$F \,:\!=\,{}_{2}{F}_1$
, it follows from Equation (2.6) that: \begin{align*} x^{n} \circledast x^m & = \frac {n! m!}{(m+n+1)!} x^{m+n+1} + \frac {x^{n}}{m+1} F\left (1,-n;\,m+2;\, \frac {-1}{x}\right )\nonumber\\[3pt]& \quad - \frac {x^{m+1}}{m+1} F(1,-n;\,m+2;\,-x).\end{align*}
\begin{align*} x^{n} \circledast x^m & = \frac {n! m!}{(m+n+1)!} x^{m+n+1} + \frac {x^{n}}{m+1} F\left (1,-n;\,m+2;\, \frac {-1}{x}\right )\nonumber\\[3pt]& \quad - \frac {x^{m+1}}{m+1} F(1,-n;\,m+2;\,-x).\end{align*}
3. Probabilistic interpretation
For positive real numbers
![]() $a,b \gt 0$
, recall that the beta
$a,b \gt 0$
, recall that the beta
![]() $(a,b)$
probability distribution, has density
$(a,b)$
probability distribution, has density
with respect the the Lebesgue measure on
![]() $\mathbb{R}$
, where
$\mathbb{R}$
, where
![]() $\Gamma$
denotes Euler’s gamma function [Reference Artin3] :
$\Gamma$
denotes Euler’s gamma function [Reference Artin3] :
The following corollary offers a probabilistic interpretations of Theorem 1.1 in terms of the fractional part of a sum of
![]() $n$
i.i.d beta
$n$
i.i.d beta
![]() $(1,2)$
-distributed random variables on the circle.
$(1,2)$
-distributed random variables on the circle.
Corollary 3.1.
The probability density of the sum of
![]() $n$
independent beta
$n$
independent beta
![]() $(1,2)$
random variables in the circle
$(1,2)$
random variables in the circle
![]() ${\mathbb{T}} ={\mathbb{R}}/ \mathbb{Z}$
is
${\mathbb{T}} ={\mathbb{R}}/ \mathbb{Z}$
is
Proof. Note that
![]() $b_0(u) = 1$
and the density of a beta
$b_0(u) = 1$
and the density of a beta
![]() $(1,2)$
random variable is
$(1,2)$
random variable is
![]() $2(1 - u) = 1 - 2b_1(u)$
for
$2(1 - u) = 1 - 2b_1(u)$
for
![]() $0 \lt u \lt 1$
. So the result follows by induction from Corollary 1.2.
$0 \lt u \lt 1$
. So the result follows by induction from Corollary 1.2.
Recall that a beta(
![]() $1,2$
) random variable can be constructed as the minimum of two independent uniform random variables in
$1,2$
) random variable can be constructed as the minimum of two independent uniform random variables in
![]() $[0,1]$
. Let
$[0,1]$
. Let
![]() $U_1, U^{\prime}_{1}, \dots,U_n,U^{\prime}_{n}$
be a sequence of
$U_1, U^{\prime}_{1}, \dots,U_n,U^{\prime}_{n}$
be a sequence of
![]() $2n$
i.i.d random random variables with uniform distribution on
$2n$
i.i.d random random variables with uniform distribution on
![]() ${\mathbb{T}} = [0,1)$
. We think of these variables as random positions around a circle of circumference
${\mathbb{T}} = [0,1)$
. We think of these variables as random positions around a circle of circumference
![]() $1$
. On the event of probability one that the
$1$
. On the event of probability one that the
![]() $U_i$
and
$U_i$
and
![]() $U^{\prime}_i$
are all distinct, we define the following variables:
$U^{\prime}_i$
are all distinct, we define the following variables:
-
1.
 $U_{1:2n} \lt U_{2:2n} \lt \cdots \lt U_{2n:2n}$
the order statistics of the variables
$U_{1:2n} \lt U_{2:2n} \lt \cdots \lt U_{2n:2n}$
the order statistics of the variables
 $U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$
,
$U_1, U^{\prime}_1, \dots, U_n, U^{\prime}_n$
, -
2.
 $X_1 \,:\!=\, \min (U_1, U^{\prime}_1)$
$X_1 \,:\!=\, \min (U_1, U^{\prime}_1)$
-
3. for
 $2 \le k \le n$
, the variable
$2 \le k \le n$
, the variable
 $X_{k}$
is the spacing around the circle from
$X_{k}$
is the spacing around the circle from
 $X_{k-1}$
to whichever of
$X_{k-1}$
to whichever of
 $U_{k}, U^{\prime}_{k}$
is encountered first moving clockwise around
$U_{k}, U^{\prime}_{k}$
is encountered first moving clockwise around
 $\mathbb{T}$
from
$\mathbb{T}$
from
 $X_{k-1}$
,
$X_{k-1}$
, -
4.
 $I_k$
is the random index in
$I_k$
is the random index in
 $\{1, \dots, 2n\}$
such that
$\{1, \dots, 2n\}$
such that
 $X_k = U_{I_k:2n}$
.
$X_k = U_{I_k:2n}$
. -
5.
 $D_n \in \{0, \dots, n-1 \}$
is the random number of full rotations around
$D_n \in \{0, \dots, n-1 \}$
is the random number of full rotations around
 $\mathbb{T}$
to find
$\mathbb{T}$
to find
 $X_n$
. This is also the number of descents in the sequence
$X_n$
. This is also the number of descents in the sequence
 $(I_1,I_2, \dots, I_n)$
; that is(3.1)
$(I_1,I_2, \dots, I_n)$
; that is(3.1) \begin{equation} D_n = \sum _{i = 1}^{n-1} 1[I_{i} \gt I_{i+1}]. \end{equation}
\begin{equation} D_n = \sum _{i = 1}^{n-1} 1[I_{i} \gt I_{i+1}]. \end{equation}
We refer to this construction as the Bernoulli clock. Figure 1 depicts an instance of the Bernoulli clock for
![]() $n=4$
.
$n=4$
.

Figure 1. The clock is a circle of circumference
![]() $1$
. Inside the circle the numbers
$1$
. Inside the circle the numbers
![]() $1,2, \ldots, 8$
index the order statistics of
$1,2, \ldots, 8$
index the order statistics of
![]() $8$
uniformly distributed random points on the circle. The corresponding numbers outside the circle are a random assignment of labels from the multiset of four pairs
$8$
uniformly distributed random points on the circle. The corresponding numbers outside the circle are a random assignment of labels from the multiset of four pairs
![]() $1^2 2^2 3^2 4^2$
. The four successive arrows delimit segments of
$1^2 2^2 3^2 4^2$
. The four successive arrows delimit segments of
![]() ${\mathbb{T}} \equiv [0,1)$
whose lengths
${\mathbb{T}} \equiv [0,1)$
whose lengths
![]() $X_1,X_2,X_3,X_4$
are independent beta
$X_1,X_2,X_3,X_4$
are independent beta
![]() $(1,2)$
random variables, while
$(1,2)$
random variables, while
![]() $(I_1,I_2,I_3,I_4)$
is the sequence of indices inside circle, at the end points of these four arrows. In this example,
$(I_1,I_2,I_3,I_4)$
is the sequence of indices inside circle, at the end points of these four arrows. In this example,
![]() $(I_1,I_2,I_3,I_4) = (1,4,6,3)$
, and the number of turns around the circle is
$(I_1,I_2,I_3,I_4) = (1,4,6,3)$
, and the number of turns around the circle is
![]() $D_4 = 1$
.
$D_4 = 1$
.
Proposition 3.2. With the above notation, the following hold
-
1. The random spacings
 $X_1, X_2, \dots, X_n$
(defined by the Bernoulli clock above) are i.i.d beta(
$X_1, X_2, \dots, X_n$
(defined by the Bernoulli clock above) are i.i.d beta(
 $1,2$
) random variables.
$1,2$
) random variables.
-
2. The random sequence of indices
 $(I_1, I_2, \dots, I_n)$
is independent of the sequence of order statistics
$(I_1, I_2, \dots, I_n)$
is independent of the sequence of order statistics
 $(U_{1:2n}, \dots, U_{2n:2n})$
.
$(U_{1:2n}, \dots, U_{2n:2n})$
.
3.1. Expanding Bernoulli polynomials in the Bernstein basis
It is well known that, for
![]() $1 \leq k \leq 2n$
the distribution of
$1 \leq k \leq 2n$
the distribution of
![]() $U_{k:2n}$
is beta(
$U_{k:2n}$
is beta(
![]() $k, 2n+1-k$
), whose probability density relative to Lebesgue measure at
$k, 2n+1-k$
), whose probability density relative to Lebesgue measure at
![]() $u \in [0,1)$
is the normalised Bernstein polynomial of degree
$u \in [0,1)$
is the normalised Bernstein polynomial of degree
![]() $2 n - 1$
$2 n - 1$
Proposition 3.3.
For each positive integer
![]() $n$
, the sum
$n$
, the sum
![]() $S_n$
of
$S_n$
of
![]() $n$
independent beta
$n$
independent beta
![]() $(1,2)$
variables has fractional part
$(1,2)$
variables has fractional part
![]() $S_n^\circ$
whose probability density on
$S_n^\circ$
whose probability density on
![]() $(0,1)$
is given by the formulas
$(0,1)$
is given by the formulas
 \begin{equation} f_{S_n}^\circ (u) = 1 - 2^n b_n(u) = \sum _{k = 1}^{2n} p_{k:2n} \ f_{k:2n}(u), \quad \text{for } u \in (0,1). \end{equation}
\begin{equation} f_{S_n}^\circ (u) = 1 - 2^n b_n(u) = \sum _{k = 1}^{2n} p_{k:2n} \ f_{k:2n}(u), \quad \text{for } u \in (0,1). \end{equation}
where
![]() $(p_{1:2n}, \dots, p_{2n:2n})$
is the probability distribution of the random index
$(p_{1:2n}, \dots, p_{2n:2n})$
is the probability distribution of the random index
![]() $I_n$
in the Bernoulli clock construction:
$I_n$
in the Bernoulli clock construction:
Proof. The first formula for the density of
![]() $S_n^\circ$
is read from Corollary 3.1. Proposition 3.2 represents
$S_n^\circ$
is read from Corollary 3.1. Proposition 3.2 represents
![]() $S_n^\circ = U_{I_n: 2n}$
where the index
$S_n^\circ = U_{I_n: 2n}$
where the index
![]() $I_n$
is independent of the sequence of order statistics
$I_n$
is independent of the sequence of order statistics
![]() $(U_{k:2n}, 1 \le k \le 2 n)$
, hence the second formula for the same probability density on
$(U_{k:2n}, 1 \le k \le 2 n)$
, hence the second formula for the same probability density on
![]() $(0,1)$
.
$(0,1)$
.
Corollary 3.4.
The factorially normalised Bernoulli polynomial of degree
![]() $n$
admits the expansion in Bernstein polynomials of degree
$n$
admits the expansion in Bernstein polynomials of degree
![]() $2 n - 1$
$2 n - 1$
 \begin{equation} b_{n}(u) = \frac{1}{2^n} \sum _{k = 1}^{2n} \delta _{k: 2n } \ f_{k:2n}(u) \end{equation}
\begin{equation} b_{n}(u) = \frac{1}{2^n} \sum _{k = 1}^{2n} \delta _{k: 2n } \ f_{k:2n}(u) \end{equation}
where
![]() $\delta _{k:2n}$
is the difference at
$\delta _{k:2n}$
is the difference at
![]() $k$
between the uniform probability distribution on
$k$
between the uniform probability distribution on
![]() $\{1, \dots, 2n \}$
and the distribution of
$\{1, \dots, 2n \}$
and the distribution of
![]() $I_n$
.
$I_n$
.
Proof. Formula (3.3) is obtained from (3.2), in the first instance as an identity of continuous functions of
![]() $u \in (0,1)$
, then as an identity of polynomials in
$u \in (0,1)$
, then as an identity of polynomials in
![]() $u$
, by virtue of the binomial expansion
$u$
, by virtue of the binomial expansion
 \begin{equation*} \sum _{k=1}^{2n} \frac {1}{2n} f_{k:2n}(u) = 1. \end{equation*}
\begin{equation*} \sum _{k=1}^{2n} \frac {1}{2n} f_{k:2n}(u) = 1. \end{equation*}
Remark 3.5. Since
![]() $b_n(1 - u) = ({-}1)^{n} b_{n}(u)$
and
$b_n(1 - u) = ({-}1)^{n} b_{n}(u)$
and
![]() $f_{k:2n}(1-u) = f_{2 n + 1 - k: 2n} (u)$
, the identity (3.3) implies that the difference between the distribution of
$f_{k:2n}(1-u) = f_{2 n + 1 - k: 2n} (u)$
, the identity (3.3) implies that the difference between the distribution of
![]() $I_n$
and the uniform distribution on
$I_n$
and the uniform distribution on
![]() $\{1, \ldots, 2 n\}$
has the symmetry
$\{1, \ldots, 2 n\}$
has the symmetry
Conjecture 3.6.
We conjecture that the discrete sequence
![]() $(\delta _{1:2n}, \dots, \delta _{2n:2n})$
approximates the Bernoulli polynomials
$(\delta _{1:2n}, \dots, \delta _{2n:2n})$
approximates the Bernoulli polynomials
![]() $b_n$
(hence also the shifted cosine functions, see (
1.7
)) as
$b_n$
(hence also the shifted cosine functions, see (
1.7
)) as
![]() $n$
becomes large, more precisely:
$n$
becomes large, more precisely:
Figure 3 does suggest that the difference
![]() $2n \pi ^n \delta _n(k) - (2\pi )^n b_n\left ( \frac{k-1}{2n-1}\right )$
gets smaller uniformly in
$2n \pi ^n \delta _n(k) - (2\pi )^n b_n\left ( \frac{k-1}{2n-1}\right )$
gets smaller uniformly in
![]() $1 \leq k \leq 2n$
as
$1 \leq k \leq 2n$
as
![]() $n$
grows, geometrically but rather slowly, like
$n$
grows, geometrically but rather slowly, like
![]() $C \rho ^n$
for a constant
$C \rho ^n$
for a constant
![]() $C \gt 0$
and
$C \gt 0$
and
![]() $\rho \approx 2^{- 1/100}$
.
$\rho \approx 2^{- 1/100}$
.

Figure 2. Plots of
![]() $2n \pi ^n \delta _n$
(dotted curve in blue),
$2n \pi ^n \delta _n$
(dotted curve in blue),
![]() $(2\pi )^n b_n(x)$
(curve in red) and their difference (dotted curve in black) for
$(2\pi )^n b_n(x)$
(curve in red) and their difference (dotted curve in black) for
![]() $n = 70, 75, 80, 85$
.
$n = 70, 75, 80, 85$
.

Figure 3. Plots of
![]() $2n \pi ^n \delta _{k:2n}$
$2n \pi ^n \delta _{k:2n}$
![]() $- (2\pi )^n b_n$
$- (2\pi )^n b_n$
![]() $(\frac{k-1}{2n -1 })$
for
$(\frac{k-1}{2n -1 })$
for
![]() $n = 100, 200, 300,$
$n = 100, 200, 300,$
![]() $ 400, 500, 600$
.
$ 400, 500, 600$
.
From (3.2) we see that we can expand the polynomial density
![]() $1 -2^n b_n(u)$
in the Bernstein basis of degree
$1 -2^n b_n(u)$
in the Bernstein basis of degree
![]() $2n - 1$
with positive coefficients. A similar expansion can obviously be achieved using Bernstein polynomials of degree
$2n - 1$
with positive coefficients. A similar expansion can obviously be achieved using Bernstein polynomials of degree
![]() $n$
, with coefficients which must add to
$n$
, with coefficients which must add to
![]() $1$
. These coefficients are easily calculated for modest values of
$1$
. These coefficients are easily calculated for modest values of
![]() $n$
(see (3.8)) which suggests the following
$n$
(see (3.8)) which suggests the following
Conjecture 3.7.
For each positive integer
![]() $n$
, the polynomial probability density
$n$
, the polynomial probability density
![]() $1 -2^n b_n(u)$
on
$1 -2^n b_n(u)$
on
![]() $[0,1)$
can be expanded in the Bernstein basis of degree
$[0,1)$
can be expanded in the Bernstein basis of degree
![]() $n$
with positive coefficients.
$n$
with positive coefficients.
Question 3.8.
More generally, what can be said about the greatest multiplier
![]() $c_n$
such that the polynomial
$c_n$
such that the polynomial
![]() $1 - c_n b_n(x)$
is a linear combination of degree
$1 - c_n b_n(x)$
is a linear combination of degree
![]() $n$
Bernstein polynomials with non-negative coefficients?
$n$
Bernstein polynomials with non-negative coefficients?
3.2. The distributions of
 $I_n$
and
$I_n$
and
 $D_n$
$D_n$
Proposition 3.9.
The distribution of
![]() $I_n$
in the Bernoulli clock construction is given by
$I_n$
in the Bernoulli clock construction is given by
 \begin{equation} \delta _{k:2n} = \frac{2^{n-1}}{n \ n!}\sum _{i = 0}^{n} \frac{\binom{k-1}{i} \binom{n}{i} }{ \binom{2n - 1}{i}} B_{n-i}, \quad \text{ for } 1 \leq k \leq 2n. \end{equation}
\begin{equation} \delta _{k:2n} = \frac{2^{n-1}}{n \ n!}\sum _{i = 0}^{n} \frac{\binom{k-1}{i} \binom{n}{i} }{ \binom{2n - 1}{i}} B_{n-i}, \quad \text{ for } 1 \leq k \leq 2n. \end{equation}
Proof. For each positive integer
![]() $N$
, in the Bernstein basis
$N$
, in the Bernstein basis
![]() $(f_{j:N})_{1 \leq j \leq N}$
of polynomials of degree at most
$(f_{j:N})_{1 \leq j \leq N}$
of polynomials of degree at most
![]() $N-1$
, it is well known that the monomial
$N-1$
, it is well known that the monomial
![]() $x^i$
can be expressed as
$x^i$
can be expressed as
 \begin{equation*} x^i = \frac {1}{N \binom {N - 1}{i}} \sum _{j = i+1}^{N} \binom {j-1}{i} f_{j:N}(x) \quad \text {for } 0 \leq i \lt N, \end{equation*}
\begin{equation*} x^i = \frac {1}{N \binom {N - 1}{i}} \sum _{j = i+1}^{N} \binom {j-1}{i} f_{j:N}(x) \quad \text {for } 0 \leq i \lt N, \end{equation*}
see [Reference Riordan35, Table 2.1] for a reference. Plugging this expansion into (1.2) yields the expansion of
![]() $b_n(x)$
in the Bernstein basis of degree
$b_n(x)$
in the Bernstein basis of degree
![]() $N-1$
for every
$N-1$
for every
![]() $N \gt n$
$N \gt n$
 \begin{equation} b_n(x) = \sum _{j = 1}^N \left (\sum _{i = 0}^{n} \frac{\binom{j-1}{i} \binom{n}{i}}{ n! N \binom{N - 1}{i}} B_{n-i} \right ) f_{j:N}(x) \qquad ( 0 \le n \lt N). \end{equation}
\begin{equation} b_n(x) = \sum _{j = 1}^N \left (\sum _{i = 0}^{n} \frac{\binom{j-1}{i} \binom{n}{i}}{ n! N \binom{N - 1}{i}} B_{n-i} \right ) f_{j:N}(x) \qquad ( 0 \le n \lt N). \end{equation}
In particular, for
![]() $N = 2 n$
comparison of this formula with (3.3) yields (3.7) and hence (3.6)
$N = 2 n$
comparison of this formula with (3.3) yields (3.7) and hence (3.6)
Remark 3.10. The error
![]() $\delta _{k:2n}$
is polynomial in
$\delta _{k:2n}$
is polynomial in
![]() $k$
and the symmetry
$k$
and the symmetry
![]() $\delta _{2n + 1 - j : 2n} = ({-}1)^n \delta _{j : 2n}$
is not obvious from (3.7).
$\delta _{2n + 1 - j : 2n} = ({-}1)^n \delta _{j : 2n}$
is not obvious from (3.7).
Let us now derive the distribution of
![]() $D_n$
explicitly. From the Bernoulli clock scheme, we can construct the random variable
$D_n$
explicitly. From the Bernoulli clock scheme, we can construct the random variable
![]() $D_n$
as follows. Let
$D_n$
as follows. Let
![]() $X_1, \dots, X_n$
be a sequence of i.i.d random variables and
$X_1, \dots, X_n$
be a sequence of i.i.d random variables and
![]() $S_n \,:\!=\, X_1 + \dots + X_n$
their sum in
$S_n \,:\!=\, X_1 + \dots + X_n$
their sum in
![]() $\mathbb{R}$
(not in the circle
$\mathbb{R}$
(not in the circle
![]() $\mathbb{T}$
), then
$\mathbb{T}$
), then
Theorem 3.11.
The distribution function of
![]() $S_n$
is given by
$S_n$
is given by
 \begin{equation*} {\mathbb {P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom {n}{k} \binom {n-k}{j} ({-}1)^{n-k-j} \frac {(x-k)_+^{2n - j}}{(2n-j)!}, \quad \quad \text {for } x \geq 0, \end{equation*}
\begin{equation*} {\mathbb {P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom {n}{k} \binom {n-k}{j} ({-}1)^{n-k-j} \frac {(x-k)_+^{2n - j}}{(2n-j)!}, \quad \quad \text {for } x \geq 0, \end{equation*}
where
![]() $x_{+}$
denotes
$x_{+}$
denotes
![]() $\max\! (x,0)$
for
$\max\! (x,0)$
for
![]() $x \in{\mathbb{R}}$
.
$x \in{\mathbb{R}}$
.
Proof. Let
![]() $\varphi$
be the Laplace transform of the
$\varphi$
be the Laplace transform of the
![]() $X_i$
’s i.e.
$X_i$
’s i.e.
We compute
![]() $\varphi _{X}$
and we obtain
$\varphi _{X}$
and we obtain
So for
![]() $n \geq 1$
, the Laplace transform of
$n \geq 1$
, the Laplace transform of
![]() $S_n$
is then given by
$S_n$
is then given by
 \begin{equation} \varphi _{S_n}(\theta ) = \left (\varphi _X(\theta )\right )^n = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{ e^{- k \theta } }{\theta ^{2n - j}}. \end{equation}
\begin{equation} \varphi _{S_n}(\theta ) = \left (\varphi _X(\theta )\right )^n = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{ e^{- k \theta } }{\theta ^{2n - j}}. \end{equation}
The transform
![]() $\varphi _{S_n}$
can be inverted term by term using the following identity
$\varphi _{S_n}$
can be inverted term by term using the following identity
We then obtain the cdf of
![]() $S_n$
as follows:
$S_n$
as follows:
 \begin{equation} {\mathbb{P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{(x-k)_+^{2n - j}}{(2n-j)!}, \quad \text{for } x \geq 0. \end{equation}
\begin{equation} {\mathbb{P}}(S_n \leq x) = 2^n \sum _{k =0}^{n}\sum _{ j = 0}^{n-k} \binom{n}{k} \binom{n-k}{j} ({-}1)^{n-k-j} \frac{(x-k)_+^{2n - j}}{(2n-j)!}, \quad \text{for } x \geq 0. \end{equation}
Remark 3.12. (3.10) was known to Lagrange in the 1700s and it appears in [Reference De Serret11, Lemme III and Corollaire I] where he said the final words on inverting Laplace transforms of the form (3.9):
-
“
 $\ldots$
mais comme cette intégration est facile par les methodes connues, nous n’entrerons pas dans un plus grand detail là-dessus; et nous terminerons même ici nos recherches, par lesquelles on doit voir qu’il ne reste plus de difficulté dans la solution des questions qu’on peut proposer à ce sujet.”
$\ldots$
mais comme cette intégration est facile par les methodes connues, nous n’entrerons pas dans un plus grand detail là-dessus; et nous terminerons même ici nos recherches, par lesquelles on doit voir qu’il ne reste plus de difficulté dans la solution des questions qu’on peut proposer à ce sujet.”
Since
![]() $S_n$
has a density, we can deduce that
$S_n$
has a density, we can deduce that
Combined with (3.11) this gives the distribution of
![]() $D_n$
explicitly. The following table gives the values of the number of permutations of the multiset
$D_n$
explicitly. The following table gives the values of the number of permutations of the multiset
![]() $1^2 \dots n^2$
for which
$1^2 \dots n^2$
for which
![]() $D_n = d$
, which we denote by
$D_n = d$
, which we denote by
![]() $\#(n;\, +, d)$
, for small values of
$\#(n;\, +, d)$
, for small values of
![]() $n$
.
$n$
.
Table 1 The table of
![]() $\#(n;\, +, d)$
$\#(n;\, +, d)$

Remark 3.13. The sequence
![]() $a(n) = \#(n;\, +, 0) = 2^{-n} (2n)! \ {\mathbb{P}}(D_n = 0)$
, which counts the number of permutations of
$a(n) = \#(n;\, +, 0) = 2^{-n} (2n)! \ {\mathbb{P}}(D_n = 0)$
, which counts the number of permutations of
![]() $1^2 \dots n^2$
for which
$1^2 \dots n^2$
for which
![]() $D_n = 0$
(the first column in Table 1), can be explicitly written using (3.11) as follows
$D_n = 0$
(the first column in Table 1), can be explicitly written using (3.11) as follows
 \begin{equation} a(n) ={\mathbb{P}}(S_n \leq 1) = \sum _{j = 0}^{n} ({-}1)^{n-j} \binom{n}{j}\frac{ (2n)!}{(2n-j)!}. \end{equation}
\begin{equation} a(n) ={\mathbb{P}}(S_n \leq 1) = \sum _{j = 0}^{n} ({-}1)^{n-j} \binom{n}{j}\frac{ (2n)!}{(2n-j)!}. \end{equation}
This integer sequence appears in many other contexts (see OEIS entry A006902), among which we mention a few:
-
1.
 $a(n)$
is the number of words on
$a(n)$
is the number of words on
 $1^2 \dots n^2$
with longest complete increasing subsequence of length
$1^2 \dots n^2$
with longest complete increasing subsequence of length
 $n$
. We shall detail this in Section 5.
$n$
. We shall detail this in Section 5. -
2.
 $a(n) = n! \ Z(\mathfrak{S}_n;\, n, n-1, \dots, 1)$
where
$a(n) = n! \ Z(\mathfrak{S}_n;\, n, n-1, \dots, 1)$
where
 $Z(\mathfrak{S}_n)$
is the cycle index of the symmetric group of order
$Z(\mathfrak{S}_n)$
is the cycle index of the symmetric group of order
 $n$
(see [Reference Stanley37, Section 1.3]).
$n$
(see [Reference Stanley37, Section 1.3]). -
3.
 $a(n) = \textrm{B}_n \left (n \cdot 0!, \ (n-1) \cdot 1!, \ (n-2)! \cdot 2!, \ \dots, \ 1 \cdot (n-1)! \right )$
, where
$a(n) = \textrm{B}_n \left (n \cdot 0!, \ (n-1) \cdot 1!, \ (n-2)! \cdot 2!, \ \dots, \ 1 \cdot (n-1)! \right )$
, where
 $\textrm{B}_n(x_1, \dots,x_n)$
is the
$\textrm{B}_n(x_1, \dots,x_n)$
is the
 $n$
th complete Bell polynomial.
$n$
th complete Bell polynomial.
4. Combinatorics of the Bernoulli clock
There are a number of known constructions of the Bernoulli numbers
![]() $B_n$
by permutation enumerations. Entringer [Reference Entringer14] showed that Euler’s presentations of the Bernoulli numbers, as coefficients in the expansions of hyperbolic and trigonometric functions, lead to explicit formulas for
$B_n$
by permutation enumerations. Entringer [Reference Entringer14] showed that Euler’s presentations of the Bernoulli numbers, as coefficients in the expansions of hyperbolic and trigonometric functions, lead to explicit formulas for
![]() $B_n$
by enumeration of alternating permutations. More recently, Graham and Zang [Reference Graham and Zang16] gave a formula for
$B_n$
by enumeration of alternating permutations. More recently, Graham and Zang [Reference Graham and Zang16] gave a formula for
![]() $B_{2n}$
by enumerating a particular subset of the set of
$B_{2n}$
by enumerating a particular subset of the set of
![]() $2^{-n}(2n)!$
permutations of the multiset
$2^{-n}(2n)!$
permutations of the multiset
![]() $1^2 \dots n^2$
of
$1^2 \dots n^2$
of
![]() $n$
pairs.
$n$
pairs.
The number of permutations of this multiset, such that for every
![]() $i \lt n$
between each pair of occurrences of
$i \lt n$
between each pair of occurrences of
![]() $i$
there is exactly one
$i$
there is exactly one
![]() $i+1$
, is
$i+1$
, is
![]() $({-}2)^n ( 1 - 2^{2 n} )B_{2n}$
. Here we offer a novel combinatorial expression of the Bernoulli numbers based on a different attribute of permutations of same multiset (1.13), which arises from the the probabilistic interpretation in Section 3. We call the combinatorial construction involved the the Bernoulli clock. Fix a positive integer
$({-}2)^n ( 1 - 2^{2 n} )B_{2n}$
. Here we offer a novel combinatorial expression of the Bernoulli numbers based on a different attribute of permutations of same multiset (1.13), which arises from the the probabilistic interpretation in Section 3. We call the combinatorial construction involved the the Bernoulli clock. Fix a positive integer
![]() $n \geq 1$
and for a permutation
$n \geq 1$
and for a permutation
![]() $\tau$
of the multiset (1.13),
$\tau$
of the multiset (1.13),
-
• Let
 $1 \leq I_1 \leq 2n-1$
be the position of the first
$1 \leq I_1 \leq 2n-1$
be the position of the first
 $1$
; that is
$1$
; that is
 $I_1 = \min \{1 \leq k \leq 2n \colon \tau (k) = 1 \}$
.
$I_1 = \min \{1 \leq k \leq 2n \colon \tau (k) = 1 \}$
. -
• For
 $1 \leq k \leq n-1$
, denote by
$1 \leq k \leq n-1$
, denote by
 $1 \leq I_{k+1} \leq 2n$
the index of the first value
$1 \leq I_{k+1} \leq 2n$
the index of the first value
 $k+1$
following
$k+1$
following
 $I_k$
in the cyclic order (circling back to the beginning of necessary).
$I_k$
in the cyclic order (circling back to the beginning of necessary). -
• Let
 $0 \leq D_n \leq n-1$
be the number of times we circled back to the beginning of the multiset before obtaining the last index
$0 \leq D_n \leq n-1$
be the number of times we circled back to the beginning of the multiset before obtaining the last index
 $I_n$
.
$I_n$
.
Example 4.1. The permutation
![]() $\tau$
corresponding to Figure 1 is the permutation
$\tau$
corresponding to Figure 1 is the permutation
![]() $\tau = (1,1,4,2,4,3,3,2)$
. For this permutation
$\tau = (1,1,4,2,4,3,3,2)$
. For this permutation
Notice that random index
![]() $I_n$
and the number of descents
$I_n$
and the number of descents
![]() $D_n$
depend only on the relative positions of
$D_n$
depend only on the relative positions of
![]() $U_1, U^{\prime}_1, \dots, U_{n},U^{\prime}_{n}$
i.e. the permutation of the multiset
$U_1, U^{\prime}_1, \dots, U_{n},U^{\prime}_{n}$
i.e. the permutation of the multiset
![]() $1^2 \dots n^2$
. So the distribution of
$1^2 \dots n^2$
. So the distribution of
![]() $I_n$
and
$I_n$
and
![]() $D_n$
can be obtained by enumerating permutations. For
$D_n$
can be obtained by enumerating permutations. For
![]() $n \geq, 1 \leq i \leq 2n$
and
$n \geq, 1 \leq i \leq 2n$
and
![]() $0 \leq d \leq n-1$
, let us denote by
$0 \leq d \leq n-1$
, let us denote by
-
1.
 $\#(n;\,i,d)$
the number of permutations among the
$\#(n;\,i,d)$
the number of permutations among the
 $(2n)!/ 2^n$
permutations of the multiset
$(2n)!/ 2^n$
permutations of the multiset
 $\{1,1, \dots, n,n\}$
that yield
$\{1,1, \dots, n,n\}$
that yield
 $I_n = i$
and
$I_n = i$
and
 $D_n = d$
,
$D_n = d$
, -
2.
 $\#(n;\, i, {+})$
the number of permutations that yield
$\#(n;\, i, {+})$
the number of permutations that yield
 $I_n = i$
,
$I_n = i$
, -
3.
 $\#(n;\, +, d)$
the number of permutations that yield
$\#(n;\, +, d)$
the number of permutations that yield
 $D_n = d$
.
$D_n = d$
.
For
![]() $n = 2$
there are
$n = 2$
there are
![]() $6$
permutations of
$6$
permutations of
![]() $\{1,1,2,2\}$
summarised in the following table
$\{1,1,2,2\}$
summarised in the following table
Table 2 Permutations of
![]() $\{1,1,2,2\}$
and corresponding values of
$\{1,1,2,2\}$
and corresponding values of
![]() $(I_2, D_2)$
$(I_2, D_2)$

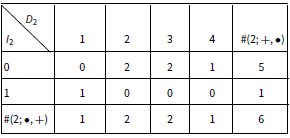
The joint distribution of
![]() $I_2, D_2$
is then given by
$I_2, D_2$
is then given by
Table 3 The table of
![]() $\#(2;\, \bullet, \bullet )$
$\#(2;\, \bullet, \bullet )$
Similarly for
![]() $n=3$
we get
$n=3$
we get
Table 4 The table of
![]() $\#(3;\, \bullet, \bullet )$
$\#(3;\, \bullet, \bullet )$

The distribution of
![]() $(I_n, D_n)$
can be obtained recursively as follows. The key observation is that every permutation of the multiset
$(I_n, D_n)$
can be obtained recursively as follows. The key observation is that every permutation of the multiset
![]() $1^2 2^2 \dots n^2$
is obtained by first choosing a permutation of
$1^2 2^2 \dots n^2$
is obtained by first choosing a permutation of
![]() $1^2 2^2 \dots (n-1)^2$
, then choosing
$1^2 2^2 \dots (n-1)^2$
, then choosing
![]() $2$
places to insert the two values
$2$
places to insert the two values
![]() $n,n$
. There are
$n,n$
. There are
![]() $\binom{2(n-1)}{2}$
options for where to insert the two last values. This corresponds to the factorisation
$\binom{2(n-1)}{2}$
options for where to insert the two last values. This corresponds to the factorisation
Moreover, for
![]() $x \in \{1, \dots, 2(n-1)\}$
the identity of quadratic polynomials
$x \in \{1, \dots, 2(n-1)\}$
the identity of quadratic polynomials
translates, for each integer
![]() $x \in \{1, \dots, 2(n-1)\}$
and each permutation
$x \in \{1, \dots, 2(n-1)\}$
and each permutation
![]() $\sigma$
of
$\sigma$
of
![]() $1^2,\dots (n-1)^2$
, the decomposition of the total number of ways to insert the next two values
$1^2,\dots (n-1)^2$
, the decomposition of the total number of ways to insert the next two values
![]() $n, n$
according to whether:
$n, n$
according to whether:
-
1. both places are to the left of
 $x$
,
$x$
, -
2. both places are to the right of
 $x$
,
$x$
, -
3. one of those places is to the left of
 $x$
and the other to the right of
$x$
and the other to the right of
 $x$
.
$x$
.
Suppose we ran the Bernoulli clock scheme on
![]() $2(n-1)$
hours and obtained
$2(n-1)$
hours and obtained
![]() $(I_{n-1}, D_{n-1})$
. Inserting two new values
$(I_{n-1}, D_{n-1})$
. Inserting two new values
![]() $n, n$
, the index
$n, n$
, the index
![]() $I_{n}$
then depends only on
$I_{n}$
then depends only on
![]() $I_{n-1}$
and the places where the two new values
$I_{n-1}$
and the places where the two new values
![]() $n$
are inserted relatively to
$n$
are inserted relatively to
![]() $I_{n-1}$
. So, the sequence
$I_{n-1}$
. So, the sequence
![]() $(I_1, I_2, \dots )$
is a time-inhomogeneous Markov chain starting from
$(I_1, I_2, \dots )$
is a time-inhomogeneous Markov chain starting from
![]() $I_1 = 1$
and a
$I_1 = 1$
and a
![]() $2(n-1) \times 2n$
transition matrix from
$2(n-1) \times 2n$
transition matrix from
![]() $I_{n-1}$
to
$I_{n-1}$
to
![]() $I_n$
given by
$I_n$
given by
where
![]() $Q_n(x,y)$
is the number of ways to insert the two new values
$Q_n(x,y)$
is the number of ways to insert the two new values
![]() $n$
in the Bernoulli clock in such a way that the first one of them to the right of
$n$
in the Bernoulli clock in such a way that the first one of them to the right of
![]() $x$
is at place
$x$
is at place
![]() $y$
. More explicitly, by elementary counting, we have
$y$
. More explicitly, by elementary counting, we have
 \begin{equation*} Q_n(x,y) = \begin {cases} x - y + 1, \quad \quad \quad \ \ \text {if } 1 \leq y \leq x \\[3pt] 2n - 1 - x, \quad \quad \quad \text {if } y = x+1 \\[3pt] 2n - y + x, \quad \quad \quad \text {if } x+2 \leq y \leq 2n \end {cases} \end{equation*}
\begin{equation*} Q_n(x,y) = \begin {cases} x - y + 1, \quad \quad \quad \ \ \text {if } 1 \leq y \leq x \\[3pt] 2n - 1 - x, \quad \quad \quad \text {if } y = x+1 \\[3pt] 2n - y + x, \quad \quad \quad \text {if } x+2 \leq y \leq 2n \end {cases} \end{equation*}
So the first few transition matrices are
 \begin{equation*} P_2 = \frac {Q_2}{\binom {4}{2}} =\frac {1}{6} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 2 & 2 & 1 \\[3pt] 2 & 1 & 1 & 2 \end {array} \right ), \quad \quad P_3 = \frac {Q_3}{\binom {6}{2}} = \frac {1}{15} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 4 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 3 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 2 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 1 & 4 \end {array} \right ), \end{equation*}
\begin{equation*} P_2 = \frac {Q_2}{\binom {4}{2}} =\frac {1}{6} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} 1 & 2 & 2 & 1 \\[3pt] 2 & 1 & 1 & 2 \end {array} \right ), \quad \quad P_3 = \frac {Q_3}{\binom {6}{2}} = \frac {1}{15} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 4 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 3 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 2 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 1 & 4 \end {array} \right ), \end{equation*}
 \begin{equation*} \text {and} \quad P_4 = \frac {Q_4}{\binom {8}{2}} = \frac {1}{28} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 6 & 6 & 5 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 5 & 6 & 5 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 4 & 6 & 5 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 3 & 6 & 5 & 4 \\[3pt] 5 & 4 & 3 & 2 & 1 & 2 & 6 & 5 \\[3pt] 6 & 5 & 4 & 3 & 2 & 1 & 1 & 6 \end {array} \right ), \end{equation*}
\begin{equation*} \text {and} \quad P_4 = \frac {Q_4}{\binom {8}{2}} = \frac {1}{28} \left ( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 6 & 6 & 5 & 4 & 3 & 2 & 1 \\[3pt] 2 & 1 & 5 & 6 & 5 & 4 & 3 & 2 \\[3pt] 3 & 2 & 1 & 4 & 6 & 5 & 4 & 3 \\[3pt] 4 & 3 & 2 & 1 & 3 & 6 & 5 & 4 \\[3pt] 5 & 4 & 3 & 2 & 1 & 2 & 6 & 5 \\[3pt] 6 & 5 & 4 & 3 & 2 & 1 & 1 & 6 \end {array} \right ), \end{equation*}
see Table 5 for a detailed combinatorial construction of
![]() $Q_3$
. This discussion is summarised by the following proposition.
$Q_3$
. This discussion is summarised by the following proposition.
Table 5 Combinatorial construction of
![]() $Q_3$
: The top
$Q_3$
: The top
![]() $1\times 6$
row displays the column index of places in rows of the main
$1\times 6$
row displays the column index of places in rows of the main
![]() $15 \times 6$
table below it. The
$15 \times 6$
table below it. The
![]() $15$
rows of the main table list all
$15$
rows of the main table list all
![]() $\binom{6}{2} = 15$
pairs of places, represented as two dots
$\binom{6}{2} = 15$
pairs of places, represented as two dots
![]() $\bullet$
, in which two new values
$\bullet$
, in which two new values
![]() $3,3$
can be inserted relative to
$3,3$
can be inserted relative to
![]() $4$
possible places of
$4$
possible places of
![]() $I_2 \in \{1, 2, 3, 4\}$
. The exponents of each dot
$I_2 \in \{1, 2, 3, 4\}$
. The exponents of each dot
![]() $\bullet$
are the values of
$\bullet$
are the values of
![]() $I_2$
leading to
$I_2$
leading to
![]() $I_3$
being the column index of that dot in
$I_3$
being the column index of that dot in
![]() $\{1,2, 3,4,5, 6 \}$
. For example in the second row, representing insertions of the new value
$\{1,2, 3,4,5, 6 \}$
. For example in the second row, representing insertions of the new value
![]() $3$
in places
$3$
in places
![]() $1$
and
$1$
and
![]() $3$
of
$3$
of
![]() $6$
places, the dot
$6$
places, the dot
![]() $\bullet ^{2,3,4}$
in place
$\bullet ^{2,3,4}$
in place
![]() $1$
is the place
$1$
is the place
![]() $I_3$
found by the Bernoulli clock algorithm if
$I_3$
found by the Bernoulli clock algorithm if
![]() $I_2 \in \{2,3,4\}$
. The matrix
$I_2 \in \{2,3,4\}$
. The matrix
![]() $Q_3$
is the
$Q_3$
is the
![]() $4 \times 6$
matrix below the main table. The entry
$4 \times 6$
matrix below the main table. The entry
![]() $Q_3(i,j)$
in row
$Q_3(i,j)$
in row
![]() $i$
and column
$i$
and column
![]() $j$
of
$j$
of
![]() $Q_3$
is the number of times
$Q_3$
is the number of times
![]() $i$
appears in the exponent of a dot
$i$
appears in the exponent of a dot
![]() $\bullet$
in the
$\bullet$
in the
![]() $j$
th column of the main table
$j$
th column of the main table

Proposition 4.2.
For a uniform random permutation of
![]() $1^2 \dots n^2$
the probability distribution of
$1^2 \dots n^2$
the probability distribution of
![]() $I_n$
, treated as a
$I_n$
, treated as a
![]() $1\times 2n$
row vector
$1\times 2n$
row vector
![]() $p_n = (p_{1:2n}, \dots, p_{2n:2n})$
, is determined recursively by the matrix forward equations
$p_n = (p_{1:2n}, \dots, p_{2n:2n})$
, is determined recursively by the matrix forward equations
So the first few of these distributions of
![]() $I_n$
are as follows:
$I_n$
are as follows:
 \begin{align*} p_1 &= (1,0), & p_2 &= \frac{1}{6} (1,2,2,1), \\[3pt] p_3 &= \frac{1}{90} (15,13,14,16,17,15), & p_4 &= \frac{1}{2520} (322,322,312,304,304,312,322,322). \end{align*}
\begin{align*} p_1 &= (1,0), & p_2 &= \frac{1}{6} (1,2,2,1), \\[3pt] p_3 &= \frac{1}{90} (15,13,14,16,17,15), & p_4 &= \frac{1}{2520} (322,322,312,304,304,312,322,322). \end{align*}
As
![]() $n$
become bigger, the distribution
$n$
become bigger, the distribution
![]() $p_{n}$
gets closer to the uniform on
$p_{n}$
gets closer to the uniform on
![]() $\{1, \dots, 2n\}$
. The error
$\{1, \dots, 2n\}$
. The error
![]() $\delta _n(k) = 1/(2n) - p_{k:2n}$
is polynomial in
$\delta _n(k) = 1/(2n) - p_{k:2n}$
is polynomial in
![]() $k$
and satisfies the same forward equation as
$k$
and satisfies the same forward equation as
![]() $p_n$
i.e.
$p_n$
i.e.
The sequence
![]() $\delta _n$
is also closely tied to the polynomial
$\delta _n$
is also closely tied to the polynomial
![]() $b_n(x)$
as (3.3) shows.
$b_n(x)$
as (3.3) shows.
Example 4.3. Let us detail the combinatorics of permutations that yields the matrix
![]() $P_3$
.
$P_3$
.
Notice that the matrices
![]() $Q_n$
have the remarkable symmetry
$Q_n$
have the remarkable symmetry
with
![]() $\widetilde{Q}_{n}(i, j) \,:\!=\, Q_{n}(2n - 1 - i, 2n + 1 -j)$
i.e. the matrix
$\widetilde{Q}_{n}(i, j) \,:\!=\, Q_{n}(2n - 1 - i, 2n + 1 -j)$
i.e. the matrix
![]() $\widetilde{Q}_n$
is the matrix
$\widetilde{Q}_n$
is the matrix
![]() $Q_n$
with entries in reverse order in both axis.
$Q_n$
with entries in reverse order in both axis.
Remark 4.4.
-
1. It is interesting to note that, from (4.1), it is not clear what the Bernoulli polynomials have in relation with the distribution
 $p_{n}$
or the error
$p_{n}$
or the error
 $\delta _n$
. It is not also clear from this recursion, even with (4.3), that
$\delta _n$
. It is not also clear from this recursion, even with (4.3), that
 $\delta _n$
has the symmetry described in (3.5).
$\delta _n$
has the symmetry described in (3.5). -
2. Considering
 $\delta _n$
as a discrete analogue of
$\delta _n$
as a discrete analogue of
 $b_n$
, one can think of the equation
$b_n$
, one can think of the equation
 $\delta _{n+1} = \delta _{n} \ P_{n+1}$
as a discrete analogue of the integral formula (1.4).
$\delta _{n+1} = \delta _{n} \ P_{n+1}$
as a discrete analogue of the integral formula (1.4). -
3. In addition to the dynamics of the Markov chain
 $I = (I_1, I_2, \dots )$
, we can get obtain the joint distribution of
$I = (I_1, I_2, \dots )$
, we can get obtain the joint distribution of
 $(I_n, D_n)$
recursively in the same way. The key observation is that at step
$(I_n, D_n)$
recursively in the same way. The key observation is that at step
 $n$
, having obtained
$n$
, having obtained
 $I_n$
from the Bernoulli clock scheme and inserting the two new values
$I_n$
from the Bernoulli clock scheme and inserting the two new values
 $n+1$
in the clock, we either increment
$n+1$
in the clock, we either increment
 $D_n$
by
$D_n$
by
 $1$
to get
$1$
to get
 $D_{n+1}$
if both values are inserted prior to
$D_{n+1}$
if both values are inserted prior to
 $I_n$
or the number of laps is not incremented i.e.
$I_n$
or the number of laps is not incremented i.e.
 $D_{n+1} = D_n$
if one of the two values is inserted after
$D_{n+1} = D_n$
if one of the two values is inserted after
 $I_n$
. We then obtain the following recursion for
$I_n$
. We then obtain the following recursion for
 $\#(n;\, i, d)$
:
$\#(n;\, i, d)$
:-
1)
 $\#(1 ;\, 1, 0) = 1$
$\#(1 ;\, 1, 0) = 1$
-
2)
 $\#(n+1;\, i, d) = \sum \limits _{1 \leq x \lt h} \#(n;\, i, x) \ \#_{n+1}(x,d) + \sum \limits _{h \leq x \leq 2n} \#(n;\, i-1, x) \ \#_{n+1}(x,d)$
.
$\#(n+1;\, i, d) = \sum \limits _{1 \leq x \lt h} \#(n;\, i, x) \ \#_{n+1}(x,d) + \sum \limits _{h \leq x \leq 2n} \#(n;\, i-1, x) \ \#_{n+1}(x,d)$
.
So one can get the joint distribution of
 $(I_n,D_n)$
recursively with
$(I_n,D_n)$
recursively with \begin{equation*} {\mathbb {P}}(I_{n} = i, \ D_n = d) = \frac {\#(n;\, i, d )}{2^{-n}(2n)!}. \end{equation*}
\begin{equation*} {\mathbb {P}}(I_{n} = i, \ D_n = d) = \frac {\#(n;\, i, d )}{2^{-n}(2n)!}. \end{equation*}
-
5. Generalised Bernoulli clock
Let
![]() $n \geq 1$
,
$n \geq 1$
,
![]() $m_1, \dots, m_n \geq 1$
be positive integers and
$m_1, \dots, m_n \geq 1$
be positive integers and
![]() $M = m_1 + \dots + m_n$
. Let
$M = m_1 + \dots + m_n$
. Let
![]() $\tau _n = \tau (m_1, \dots, m_n)$
be a random permutation uniformly distributed among the
$\tau _n = \tau (m_1, \dots, m_n)$
be a random permutation uniformly distributed among the
![]() $M!/(m_1 ! \dots m_n !)$
permutations of the multiset
$M!/(m_1 ! \dots m_n !)$
permutations of the multiset
![]() $1^{m_1}2^{m_2} \dots n^{m_n}$
. Let us denote by
$1^{m_1}2^{m_2} \dots n^{m_n}$
. Let us denote by
![]() $1 \leq I_1 \leq M$
the index of the first
$1 \leq I_1 \leq M$
the index of the first
![]() $1$
in the sequence
$1$
in the sequence
![]() $\tau _n$
. Continuing from this index
$\tau _n$
. Continuing from this index
![]() $I_1$
, let
$I_1$
, let
![]() $I_2$
be the index of the first
$I_2$
be the index of the first
![]() $2$
we encounter (circling back if necessary) and continuing in this manner we get random indices
$2$
we encounter (circling back if necessary) and continuing in this manner we get random indices
![]() $(I_1, I_2, \dots, I_n)$
. Let us denote by
$(I_1, I_2, \dots, I_n)$
. Let us denote by
![]() $D_n = D(m_1, \dots, m_n)$
the number of times we circled around the sequence
$D_n = D(m_1, \dots, m_n)$
the number of times we circled around the sequence
![]() $\tau _n$
in this process, that is the number of descents in the random sequence
$\tau _n$
in this process, that is the number of descents in the random sequence
![]() $(I_1, I_2, \dots, I_n)$
, as in (3.1).
$(I_1, I_2, \dots, I_n)$
, as in (3.1).
For the continuous model, mark the circle
![]() ${\mathbb{T}} ={\mathbb{R}}/\mathbb{Z} \cong [0,1)$
with
${\mathbb{T}} ={\mathbb{R}}/\mathbb{Z} \cong [0,1)$
with
![]() $M$
i.i.d uniform on
$M$
i.i.d uniform on
![]() $[0,1]$
random variables
$[0,1]$
random variables
![]() $U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$
, …,
$U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$
, …,
![]() $U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$
and let
$U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$
and let
![]() $U_{1:M} \lt \cdots \lt U_{M:M}$
be their order statistics. Starting from
$U_{1:M} \lt \cdots \lt U_{M:M}$
be their order statistics. Starting from
![]() $0$
we walk around the clock until we encounter the first of the variables
$0$
we walk around the clock until we encounter the first of the variables
![]() $U_{1}^{(i)}$
at some random index
$U_{1}^{(i)}$
at some random index
![]() $I_1$
. We continue from the random index
$I_1$
. We continue from the random index
![]() $I_1$
until we encounter the first of the variables
$I_1$
until we encounter the first of the variables
![]() $U_{2}^{(i)}$
(circling back if necessary) and continue like this until we encounter the first of the variables
$U_{2}^{(i)}$
(circling back if necessary) and continue like this until we encounter the first of the variables
![]() $U_{n}^{(i)}$
. We then obtain the random sequence
$U_{n}^{(i)}$
. We then obtain the random sequence
![]() $(I_1, I_2, \dots, I_n)$
and
$(I_1, I_2, \dots, I_n)$
and
![]() $D_{n}$
is the number of times we circled around the clock. Finally, let us denote by
$D_{n}$
is the number of times we circled around the clock. Finally, let us denote by
![]() $(X_1, \dots, X_n)$
the lengths (clockwise) of the segments
$(X_1, \dots, X_n)$
the lengths (clockwise) of the segments
![]() $[U_{I_1:M}, U_{I_2:M}]$
,
$[U_{I_1:M}, U_{I_2:M}]$
,
![]() $\dots$
,
$\dots$
,
![]() $[U_{I_{n-1}:M}, U_{I_{n}:M}]$
,
$[U_{I_{n-1}:M}, U_{I_{n}:M}]$
,
![]() $ [U_{I_{n}:M}, U_{I_{1}:M}]$
on the clock. The model described in Section 4 is the particular instance of this model where
$ [U_{I_{n}:M}, U_{I_{1}:M}]$
on the clock. The model described in Section 4 is the particular instance of this model where
![]() $m_1 = \dots = m_n = 2$
.
$m_1 = \dots = m_n = 2$
.
Remark 5.1. When there is no risk of confusion, we shall suppress the parameters
![]() $m_1, \dots, m_n$
to simplify the notation.
$m_1, \dots, m_n$
to simplify the notation.
Proposition 5.2. The following hold
-
1. The random lengths
 $X_1, X_2, \dots, X_n$
are independent random variables and
$X_1, X_2, \dots, X_n$
are independent random variables and
 $X_i$
has distribution beta(
$X_i$
has distribution beta(
 $1,m_i$
) for each
$1,m_i$
) for each
 $ 1 \leq i \leq n$
.
$ 1 \leq i \leq n$
. -
2. The random sequence of indices
 $(I_1, I_2, \dots, I_n)$
is independent of the order statistics
$(I_1, I_2, \dots, I_n)$
is independent of the order statistics
 $(U_{1:M} \lt \cdots \lt U_{M:M})$
.
$(U_{1:M} \lt \cdots \lt U_{M:M})$
.
Proof. Notice that
![]() $X_1 = \min (U_1^{(1)}, \dots, U_1^{(m_1)})$
is a beta(
$X_1 = \min (U_1^{(1)}, \dots, U_1^{(m_1)})$
is a beta(
![]() $1,m_1$
) random variable. Also, since
$1,m_1$
) random variable. Also, since
![]() $U_2^{(1)}, \dots, U_2^{(m_2)}$
are i.i.d uniform and are independent of the position of
$U_2^{(1)}, \dots, U_2^{(m_2)}$
are i.i.d uniform and are independent of the position of
![]() $X_1$
on the circle, the variables
$X_1$
on the circle, the variables
![]() $U_2^{(i)} - X_1 \mod \mathbb{Z} \in [0,1)$
are still i.i.d uniform so
$U_2^{(i)} - X_1 \mod \mathbb{Z} \in [0,1)$
are still i.i.d uniform so
![]() $X_2$
is also beta(
$X_2$
is also beta(
![]() $1,m_2$
) and independent of
$1,m_2$
) and independent of
![]() $X_1$
. Running the same argument repeatedly we deduce that the variables
$X_1$
. Running the same argument repeatedly we deduce that the variables
![]() $X_1, X_2 \dots, X_n$
are independent with
$X_1, X_2 \dots, X_n$
are independent with
![]() $X_i \sim \textrm{beta}(1,m_i)$
. Also, the random index
$X_i \sim \textrm{beta}(1,m_i)$
. Also, the random index
![]() $I_n$
at which the process stops depends only on the relative positions of the variables
$I_n$
at which the process stops depends only on the relative positions of the variables
![]() $U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$
, …,
$U_{1}^{(1)}, \dots, U_{1}^{(m_1)}$
, …,
![]() $U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$
i.e.
$U_{n}^{(1)}, \dots, U_{n}^{(m_n)}$
i.e.
![]() $I_n$
is fully determined by the random permutation of
$I_n$
is fully determined by the random permutation of
![]() $\{1,\dots, M\}$
induced by the
$\{1,\dots, M\}$
induced by the
![]() $M$
i.i.d uniforms. We then deduce that
$M$
i.i.d uniforms. We then deduce that
![]() $I_n$
is independent of the order statistics
$I_n$
is independent of the order statistics
![]() $(U_{1:M} \lt U_{2:M} \lt \cdots \lt U_{M:M})$
.
$(U_{1:M} \lt U_{2:M} \lt \cdots \lt U_{M:M})$
.
The number
![]() $D_{n}$
of turns around the clock can also be expressed as follows
$D_{n}$
of turns around the clock can also be expressed as follows
Let us denote by
![]() $L_n = L(m_1, m_2, \dots, m_n)$
the length of the longest continuous increasing subsequence of
$L_n = L(m_1, m_2, \dots, m_n)$
the length of the longest continuous increasing subsequence of
![]() $\tau _n$
starting with
$\tau _n$
starting with
![]() $1$
; that is the largest integer
$1$
; that is the largest integer
![]() $1\leq \ell \leq n$
such that
$1\leq \ell \leq n$
such that
Example 5.3. Suppose
![]() $n = 4$
and
$n = 4$
and
![]() $(m_1,m_2,m_3,m_4) = (2,3,2,4)$
and consider the permutation
$(m_1,m_2,m_3,m_4) = (2,3,2,4)$
and consider the permutation
![]() $\tau _n = ({1},4,4,1,4,{2 },4,{3},3,2,2)$
. The the longest increasing continuous subsequence of
$\tau _n = ({1},4,4,1,4,{2 },4,{3},3,2,2)$
. The the longest increasing continuous subsequence of
![]() $\tau _n$
starting from
$\tau _n$
starting from
![]() $1$
(the boldfaced subsequence) has length
$1$
(the boldfaced subsequence) has length
![]() $L_4 = 3$
in this case.
$L_4 = 3$
in this case.
For an infinite sequence
![]() $m = (m_1,m_2, \dots )$
of positive integers, notice that we can construct the sequences of variables
$m = (m_1,m_2, \dots )$
of positive integers, notice that we can construct the sequences of variables
![]() $L_n = L(m_1,\dots, m_n)$
,
$L_n = L(m_1,\dots, m_n)$
,
![]() $D_n = D(m_1,\dots, m_n)$
and
$D_n = D(m_1,\dots, m_n)$
and
![]() $I_n = I(m_1, \dots, m_n)$
on a common probability space. This is done by marking an additional
$I_n = I(m_1, \dots, m_n)$
on a common probability space. This is done by marking an additional
![]() $m_n$
i.i.d uniform positions on the circle
$m_n$
i.i.d uniform positions on the circle
![]() $\mathbb{T}$
at each step
$\mathbb{T}$
at each step
![]() $n$
. Notice then that
$n$
. Notice then that
![]() $(L_n = L(m_1, \dots, m_n))_{n \geq 1}$
is an increasing sequence of random variables so we define
$(L_n = L(m_1, \dots, m_n))_{n \geq 1}$
is an increasing sequence of random variables so we define
Proposition 5.4. We have the following
 \begin{equation*} L_{n} = \sum _{ k = 0 }^{n} 1[S_k \leq 1] \quad \text {and} \quad L_{\infty } = \sum _{k = 0}^{\infty } 1[S_k \leq 1]. \end{equation*}
\begin{equation*} L_{n} = \sum _{ k = 0 }^{n} 1[S_k \leq 1] \quad \text {and} \quad L_{\infty } = \sum _{k = 0}^{\infty } 1[S_k \leq 1]. \end{equation*}
In particular, we have
![]() $(L_n = n) = (D_n = 0)$
and for
$(L_n = n) = (D_n = 0)$
and for
![]() $n \geq k$
we have
$n \geq k$
we have
Proof. The length
![]() $L_n$
of the longest sequence of the form
$L_n$
of the longest sequence of the form
![]() $1 \dots \ell$
is the maximal integer
$1 \dots \ell$
is the maximal integer
![]() $\ell$
such that
$\ell$
such that
![]() $S_\ell \leq 1$
, i.e. the maximal
$S_\ell \leq 1$
, i.e. the maximal
![]() $l$
such that the random walk
$l$
such that the random walk
![]() $(S_k)_{k\geq 0}$
does not shoot over
$(S_k)_{k\geq 0}$
does not shoot over
![]() $1$
. Then we deduce that indeed
$1$
. Then we deduce that indeed
The rest of the statements follow immediately from this equation.
Corollary 5.5.
For
![]() $k \leq n$
we have
$k \leq n$
we have
Proof. Follows immediately from Proposition 5.4.
Remark 5.6. When
![]() $m_1 = m_2 = \dots m_n = 1$
, the random variable
$m_1 = m_2 = \dots m_n = 1$
, the random variable
![]() $S_n$
is the sum of
$S_n$
is the sum of
![]() $n$
i.i.d uniform random variables on
$n$
i.i.d uniform random variables on
![]() $[0,1]$
and the fractional part
$[0,1]$
and the fractional part
![]() $S_n^\circ$
has uniform distribution on
$S_n^\circ$
has uniform distribution on
![]() $\mathbb{T}$
. The index
$\mathbb{T}$
. The index
![]() $I_n$
has uniform distribution in
$I_n$
has uniform distribution in
![]() $\{1,\dots, n\}$
and the distribution of the number of descents
$\{1,\dots, n\}$
and the distribution of the number of descents
is given by the Eulerian numbers
![]() $A_{n,k}$
, see [Reference Stanley37, Section 1.4].
$A_{n,k}$
, see [Reference Stanley37, Section 1.4].
Horton and Kurn [Reference Horton and Kurn18, Theorem and Corollary (c)] gives a formula for the number of permutations
![]() $\tau$
of the multiset
$\tau$
of the multiset
![]() $1^{m_1}2^{m_2}\dots n^{m_n}$
for which
$1^{m_1}2^{m_2}\dots n^{m_n}$
for which
![]() $L_n = n$
; that is a formula for
$L_n = n$
; that is a formula for
We shall interpret this formula in our context and rederive it from a probabilistic perspective.
Theorem 5.7.
The number of permutations
![]() $\tau _n$
of the multiset
$\tau _n$
of the multiset
![]() $1^{m_1} 2 ^{m_2} \dots n^{m_n}$
that contain the sequence
$1^{m_1} 2 ^{m_2} \dots n^{m_n}$
that contain the sequence
![]() $(1,2,\dots,n)$
is given by
$(1,2,\dots,n)$
is given by
 \begin{equation} \frac{M!}{m_1! \dots m_n!}{\mathbb{P}}(L_n = n) = ({-}1)^M \sum _{j = 0}^{M} \binom{M}{j} \frac{c_{j}}{j!}, \end{equation}
\begin{equation} \frac{M!}{m_1! \dots m_n!}{\mathbb{P}}(L_n = n) = ({-}1)^M \sum _{j = 0}^{M} \binom{M}{j} \frac{c_{j}}{j!}, \end{equation}
where
with
![]() $[x^n] f(x)$
denoting the coefficient of
$[x^n] f(x)$
denoting the coefficient of
![]() $x^n$
in the power series expansion of
$x^n$
in the power series expansion of
![]() $f$
.
$f$
.
Proof. Similarly to our discussion in Section 3, we can obtain an expression for
![]() ${\mathbb{P}}(S_{n} \leq x)$
by inverting the Laplace transform of
${\mathbb{P}}(S_{n} \leq x)$
by inverting the Laplace transform of
![]() $S_{n}$
. First recall that the Laplace transform of
$S_{n}$
. First recall that the Laplace transform of
![]() $X_i \sim \textrm{beta}(1,m_i)$
is
$X_i \sim \textrm{beta}(1,m_i)$
is
where
![]() $E_k(x)$
denotes the exponential polynomial
$E_k(x)$
denotes the exponential polynomial
![]() $E_k(x) = \sum \limits _{i = 0}^{k} x^i/i!$
. So the Laplace transform of
$E_k(x) = \sum \limits _{i = 0}^{k} x^i/i!$
. So the Laplace transform of
![]() $S_{n}$
is then given by
$S_{n}$
is then given by
 \begin{equation*} \varphi _{S_{n}}(\theta ) = \frac {({-}1)^M \prod \limits _{i=1}^{n} m_i !} {\theta ^M} \prod _{i = 1}^{n} \left ( e^{-\theta } - E_{m_i - 1}({-}\theta )\right ). \end{equation*}
\begin{equation*} \varphi _{S_{n}}(\theta ) = \frac {({-}1)^M \prod \limits _{i=1}^{n} m_i !} {\theta ^M} \prod _{i = 1}^{n} \left ( e^{-\theta } - E_{m_i - 1}({-}\theta )\right ). \end{equation*}
Using (3.10) to invert this Laplace transform, we get
 \begin{equation*} {\mathbb {P}}(S_{n} \leq x) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{k, j \geq 0} \alpha _{k,j} \frac {(x-k)^{M-j}_+ }{(M-j)!}, \end{equation*}
\begin{equation*} {\mathbb {P}}(S_{n} \leq x) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{k, j \geq 0} \alpha _{k,j} \frac {(x-k)^{M-j}_+ }{(M-j)!}, \end{equation*}
where
![]() $\alpha _{k,j}$
is the coefficient of
$\alpha _{k,j}$
is the coefficient of
![]() $\theta ^j X^k$
in the polynomial
$\theta ^j X^k$
in the polynomial
![]() $\prod _{i=1}^n (X - E_{m_i - 1}({-}\theta ))$
. So we deduce that
$\prod _{i=1}^n (X - E_{m_i - 1}({-}\theta ))$
. So we deduce that
 \begin{equation*} {\mathbb {P}}(L_n = n) = {\mathbb {P}}(S_n \leq 1) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{j = 0}^{M} \frac {c_{j}}{(M-j)!}, \end{equation*}
\begin{equation*} {\mathbb {P}}(L_n = n) = {\mathbb {P}}(S_n \leq 1) = ({-}1)^M \left (\prod \limits _{i=1}^{n} m_i ! \right ) \sum _{j = 0}^{M} \frac {c_{j}}{(M-j)!}, \end{equation*}
with
 \begin{equation*} c_j = \alpha _{0,j} = ({-}1)^n [\theta ^j] \left ( \prod _{i = 1}^{n} E_{m_i - 1}({-} \theta ) \right ). \end{equation*}
\begin{equation*} c_j = \alpha _{0,j} = ({-}1)^n [\theta ^j] \left ( \prod _{i = 1}^{n} E_{m_i - 1}({-} \theta ) \right ). \end{equation*}
Multiplying by
![]() $ M!/ (m_1! \dots m_n!)$
we get the formula (5.2).
$ M!/ (m_1! \dots m_n!)$
we get the formula (5.2).
We suppose from now on that
![]() $m \,:\!=\, m_1 = m_2 = \dots \geq 1$
. Let
$m \,:\!=\, m_1 = m_2 = \dots \geq 1$
. Let
![]() $\mathcal{L}_{n,m}$
and
$\mathcal{L}_{n,m}$
and
![]() $\mathcal{L}_{m}$
denote the expectation of
$\mathcal{L}_{m}$
denote the expectation of
![]() $L_n$
and
$L_n$
and
![]() $L_\infty$
; that is
$L_\infty$
; that is
In [Reference Clifton, Deb, Huang, Spiro and Yoo8], the authors present a fine asymptotic study of
![]() $\mathcal{L}_{m}$
as
$\mathcal{L}_{m}$
as
![]() $m \to \infty$
. In this paper, we provide a pleasant probabilistic framework in which the discussion [Reference Clifton, Deb, Huang, Spiro and Yoo8] fits rather naturally.
$m \to \infty$
. In this paper, we provide a pleasant probabilistic framework in which the discussion [Reference Clifton, Deb, Huang, Spiro and Yoo8] fits rather naturally.
Let
![]() $(N(t), t \geq 0)$
be the renewal process with beta(
$(N(t), t \geq 0)$
be the renewal process with beta(
![]() $1,m$
)-distributed i.i.d jumps
$1,m$
)-distributed i.i.d jumps
![]() $X_i$
i.e.
$X_i$
i.e.
 \begin{equation*} N(t) = \sum _{n \geq 1}^{\infty } 1[S_n \leq t]. \end{equation*}
\begin{equation*} N(t) = \sum _{n \geq 1}^{\infty } 1[S_n \leq t]. \end{equation*}
Notice that, by virtue of Proposition 5.4, the variable
![]() $N(1) = L_\infty - 1$
is the number of renewals of
$N(1) = L_\infty - 1$
is the number of renewals of
![]() $N$
in
$N$
in
![]() $[0,1]$
. Let
$[0,1]$
. Let
![]() $M(t) \,:\!=\, \mathbb{E}[N(t)]$
denote the mean of
$M(t) \,:\!=\, \mathbb{E}[N(t)]$
denote the mean of
![]() $N(t)$
. By first step analysis,
$N(t)$
. By first step analysis,
![]() $M(t)$
satisfies the following equation for
$M(t)$
satisfies the following equation for
![]() $t \in [0,1]$
:
$t \in [0,1]$
:
 \begin{align} M(t) &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx, \\[3pt] &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(x) (1 - t + x)^{m-1} dx. \nonumber \end{align}
\begin{align} M(t) &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx, \\[3pt] &={\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(x) (1 - t + x)^{m-1} dx. \nonumber \end{align}
From (5.3) we can deduce that
![]() $M$
satisfies the following differential equation
$M$
satisfies the following differential equation
 \begin{equation} 1 + \sum _{k = 0}^{m} \frac{({-}1)^{k}}{k!} M^{(k)}(t) = 0. \end{equation}
\begin{equation} 1 + \sum _{k = 0}^{m} \frac{({-}1)^{k}}{k!} M^{(k)}(t) = 0. \end{equation}
Theorem 5.8.
Let
![]() $\alpha _1, \dots, \alpha _m$
be the
$\alpha _1, \dots, \alpha _m$
be the
![]() $m$
distinct complex roots of the exponential polynomial
$m$
distinct complex roots of the exponential polynomial
![]() $E_m(x) = \sum _{k = 0}^{m} x^k/k!$
. Then the mean function
$E_m(x) = \sum _{k = 0}^{m} x^k/k!$
. Then the mean function
![]() $M(t)$
is given by
$M(t)$
is given by
Before we prove Theorem 5.8, we first recall a couple of intermediate results.
Lemma 5.9.
Let
![]() $z$
be a non-zero complex number. Then, for any positive integer
$z$
be a non-zero complex number. Then, for any positive integer
![]() $n$
and
$n$
and
![]() $t \in [0,1]$
, we have the following:
$t \in [0,1]$
, we have the following:
 \begin{equation*} \int _{0}^{t} e^{z x} (1-x)^{n} dx = n! \sum _{j = 0}^{n} \frac { e^{zt}(1-t)^j - 1}{j!} z^{j-n-1}. \end{equation*}
\begin{equation*} \int _{0}^{t} e^{z x} (1-x)^{n} dx = n! \sum _{j = 0}^{n} \frac { e^{zt}(1-t)^j - 1}{j!} z^{j-n-1}. \end{equation*}
Proof. Follows immediately by induction on
![]() $n$
and integration by parts.
$n$
and integration by parts.
The following lemma is an adaptation of [Reference Zemyan40, Theorem 7].
Lemma 5.10.
Let
![]() $\alpha _1, \dots, \alpha _m$
be the
$\alpha _1, \dots, \alpha _m$
be the
![]() $m$
distinct complex zeros of
$m$
distinct complex zeros of
![]() $E_m(x)$
. Then we have the following
$E_m(x)$
. Then we have the following
 \begin{equation*} \sum _{k = 1}^{m} \alpha _k^{-j} = \begin {cases} -1, \quad &\text {if } j = 1,\\[3pt] 0, \quad &\text {if } 2 \leq j \leq m,\\[3pt] 1/m!, \quad &\text {if } j = m+1. \end {cases} \end{equation*}
\begin{equation*} \sum _{k = 1}^{m} \alpha _k^{-j} = \begin {cases} -1, \quad &\text {if } j = 1,\\[3pt] 0, \quad &\text {if } 2 \leq j \leq m,\\[3pt] 1/m!, \quad &\text {if } j = m+1. \end {cases} \end{equation*}
Proof of Theorem
5.8. The mean function
![]() $M(t)$
satisfies (5.4). The latter is an order
$M(t)$
satisfies (5.4). The latter is an order
![]() $m$
ODE with constant coefficients and its characteristic polynomial is
$m$
ODE with constant coefficients and its characteristic polynomial is
![]() $E_m({-}x)$
whose roots are
$E_m({-}x)$
whose roots are
![]() $-\alpha _1, \dots, - \alpha _m$
. So the solution is of the form
$-\alpha _1, \dots, - \alpha _m$
. So the solution is of the form
Setting
![]() $\beta _k = - \alpha _k^{-1}$
for
$\beta _k = - \alpha _k^{-1}$
for
![]() $1 \leq k \leq m$
, it suffices to show that
$1 \leq k \leq m$
, it suffices to show that
![]() $M(t)$
satisfies (5.3). To that end notice that, thanks to Lemma 5.9, we have
$M(t)$
satisfies (5.3). To that end notice that, thanks to Lemma 5.9, we have
 \begin{align*} &{\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx\\[3pt] &\quad= m \int _{0}^{t} (1+M(t-x)) (1-x)^{m-1} dx\\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} \int _{0}^{t} e^{-\alpha _k (t-x)} (1-x)^{m-1} dx \\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} \int _{0}^{t} e^{\alpha _k x} (1-x)^{m-1} dx \\[3pt] &\quad= \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} (m-1)! \sum _{j = 0}^{m-1} \frac{1 - e^{\alpha _k t}(1-t)^j}{j!} \alpha _k^{j - m}\\[3pt] &\quad= m! \sum _{k = 1}^{m} \sum _{j = 0}^{m-1} \frac{e^{-\alpha _k t} - (1-t)^j}{j!} \alpha _k^{j-m-1}. \end{align*}
\begin{align*} &{\mathbb{P}}(X_1 \leq t) + m \int _{0}^{t} M(t-x) (1-x)^{m-1} dx\\[3pt] &\quad= m \int _{0}^{t} (1+M(t-x)) (1-x)^{m-1} dx\\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} \int _{0}^{t} e^{-\alpha _k (t-x)} (1-x)^{m-1} dx \\[3pt] &\quad= - \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} \int _{0}^{t} e^{\alpha _k x} (1-x)^{m-1} dx \\[3pt] &\quad= \sum _{k = 1}^{m} m \alpha _k^{-1} e^{-\alpha _k t} (m-1)! \sum _{j = 0}^{m-1} \frac{1 - e^{\alpha _k t}(1-t)^j}{j!} \alpha _k^{j - m}\\[3pt] &\quad= m! \sum _{k = 1}^{m} \sum _{j = 0}^{m-1} \frac{e^{-\alpha _k t} - (1-t)^j}{j!} \alpha _k^{j-m-1}. \end{align*}
Now notice that, thanks to Lemma 5.10, we have
 \begin{equation*} \sum _{j=0}^{m-1} \sum _{k=1}^{m} \frac {(1-t)^j}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} = \frac {1}{m!}. \end{equation*}
\begin{equation*} \sum _{j=0}^{m-1} \sum _{k=1}^{m} \frac {(1-t)^j}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} = \frac {1}{m!}. \end{equation*}
We also have
 \begin{equation*} \sum _{k=1}^{m} \sum _{j=0}^{m-1} \frac {e^{-\alpha _k t}}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} e^{-\alpha _k t} \sum _{j=0}^{m-1} \frac {\alpha ^j}{j!} = - \frac {1}{m!} \sum _{k=1}^{m} \alpha _k^{-1} e^{-\alpha _k t}. \end{equation*}
\begin{equation*} \sum _{k=1}^{m} \sum _{j=0}^{m-1} \frac {e^{-\alpha _k t}}{j!} \alpha _k^{j-m-1} = \sum _{k=1}^{m} \alpha _k^{-m-1} e^{-\alpha _k t} \sum _{j=0}^{m-1} \frac {\alpha ^j}{j!} = - \frac {1}{m!} \sum _{k=1}^{m} \alpha _k^{-1} e^{-\alpha _k t}. \end{equation*}
The last equation follows from the fact that
![]() $\alpha _k$
is a zero of
$\alpha _k$
is a zero of
![]() $E_m(x) = \sum _{j = 0}^{m} x^j/ j!$
. So combining the last two equations with the previous one, we get
$E_m(x) = \sum _{j = 0}^{m} x^j/ j!$
. So combining the last two equations with the previous one, we get
Corollary 5.11 (Theorem 1.1-(a) in [Reference Clifton, Deb, Huang, Spiro and Yoo8]). The expectation
![]() $\mathcal{L}_{m}$
is given by
$\mathcal{L}_{m}$
is given by
In particular we have
Proof. Since
![]() $L_\infty = 1 + N(1)$
, we deduce that
$L_\infty = 1 + N(1)$
, we deduce that
![]() $\mathcal{L}_{m} = 1 + M(1)$
and the result follows immediately from Theorem 5.8.
$\mathcal{L}_{m} = 1 + M(1)$
and the result follows immediately from Theorem 5.8.
Remark 5.12. Note that derivatives of
![]() $M$
at
$M$
at
![]() $0$
are the moments of the roots
$0$
are the moments of the roots
![]() $\alpha _1, \dots, \alpha _m$
i.e.
$\alpha _1, \dots, \alpha _m$
i.e.
The functional equation (5.3) then gives a recursion that these moments satisfy:
 \begin{equation*} \mu ({-}1,m) = 0 \quad \text {and} \quad \mu (j,m) = (m)_{j+1} - \sum _{i = 0}^{j-1} \ (m)_{i+1} \mu (j-i-1,m), \quad \text {for } j \geq 0. \end{equation*}
\begin{equation*} \mu ({-}1,m) = 0 \quad \text {and} \quad \mu (j,m) = (m)_{j+1} - \sum _{i = 0}^{j-1} \ (m)_{i+1} \mu (j-i-1,m), \quad \text {for } j \geq 0. \end{equation*}
where
![]() $(X)_k = X(X-1)\dots (X-k+1)$
is the
$(X)_k = X(X-1)\dots (X-k+1)$
is the
![]() $k$
th falling factorial polynomial. These moments are polynomials
$k$
th falling factorial polynomial. These moments are polynomials
![]() $\mu (j,\cdot )$
in
$\mu (j,\cdot )$
in
![]() $m$
and it would be interesting to give an expression for
$m$
and it would be interesting to give an expression for
![]() $\mu (j,X)$
and study its properties as suggested in [Reference Zemyan40].
$\mu (j,X)$
and study its properties as suggested in [Reference Zemyan40].
To conclude this section, we give a positive answer to Conjectures 4.1 and 4.2 of [Reference Clifton, Deb, Huang, Spiro and Yoo8]. For any integer
![]() $m \geq 1$
, let
$m \geq 1$
, let
![]() $X_1^{(m)}, X_2^{(m)}, \dots$
be a sequence of i.i.d random variables with beta(
$X_1^{(m)}, X_2^{(m)}, \dots$
be a sequence of i.i.d random variables with beta(
![]() $1,m$
) distribution and denote by
$1,m$
) distribution and denote by
![]() $L_{n,m}$
and
$L_{n,m}$
and
![]() $L_{\infty, m}$
the following random variables
$L_{\infty, m}$
the following random variables
 \begin{equation*} L_{n,m} = \sum _{k = 1}^{n} 1\left [S^{(m)}_k \leq 1\right ] \quad \text {and} \quad L_{\infty, m} = \sum _{k = 1}^{\infty } 1\left [S^{(m)}_k \leq 1\right ], \end{equation*}
\begin{equation*} L_{n,m} = \sum _{k = 1}^{n} 1\left [S^{(m)}_k \leq 1\right ] \quad \text {and} \quad L_{\infty, m} = \sum _{k = 1}^{\infty } 1\left [S^{(m)}_k \leq 1\right ], \end{equation*}
with
Proposition 5.13.
The random variable
![]() $(L_{\infty, m} - m)/ \sqrt{m}$
converges in distribution to a Gaussian measure with mean
$(L_{\infty, m} - m)/ \sqrt{m}$
converges in distribution to a Gaussian measure with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
.
$1$
.
Proof. For
![]() $m \geq 1$
and
$m \geq 1$
and
![]() $x \in{\mathbb{R}}$
let
$x \in{\mathbb{R}}$
let
![]() $u(x,m) \,:\!=\, \lfloor m + x \sqrt{m} \rfloor$
. We then have
$u(x,m) \,:\!=\, \lfloor m + x \sqrt{m} \rfloor$
. We then have
 \begin{align*}{\mathbb{P}}\left ( \frac{L_{\infty, m} - m}{\sqrt{m}} \leq x \right ) &={\mathbb{P}}\left (L_{\infty, m} \leq m + x\sqrt{m}\right )\\[3pt] &={\mathbb{P}}\left (L_{\infty, m} \leq u(x,m) \right )\\[3pt] &={\mathbb{P}}\left (S_{u(x,m) + 1} \gt 1 \right )\\[3pt] &={\mathbb{P}}\left ( \frac{ m S_{u(x,m) + 1} - u(x,m) }{\sqrt{u(x,m)}} \gt \frac{ m - u(x,m)}{\sqrt{u(x,m)}} \right ). \end{align*}
\begin{align*}{\mathbb{P}}\left ( \frac{L_{\infty, m} - m}{\sqrt{m}} \leq x \right ) &={\mathbb{P}}\left (L_{\infty, m} \leq m + x\sqrt{m}\right )\\[3pt] &={\mathbb{P}}\left (L_{\infty, m} \leq u(x,m) \right )\\[3pt] &={\mathbb{P}}\left (S_{u(x,m) + 1} \gt 1 \right )\\[3pt] &={\mathbb{P}}\left ( \frac{ m S_{u(x,m) + 1} - u(x,m) }{\sqrt{u(x,m)}} \gt \frac{ m - u(x,m)}{\sqrt{u(x,m)}} \right ). \end{align*}
Denote by
![]() $(Y_{k,m})$
the array defined as follows:
$(Y_{k,m})$
the array defined as follows:
We then have
![]() $\mathbb{E}[Y_{k,m}] = 0$
and this array satisfies the conditions for the Lindeberg-Feller theorem [Reference Durrett13, Theorem 3.4.10], see Section B. Applying this theorem yields
$\mathbb{E}[Y_{k,m}] = 0$
and this array satisfies the conditions for the Lindeberg-Feller theorem [Reference Durrett13, Theorem 3.4.10], see Section B. Applying this theorem yields
but since
![]() $m - u(x,m) \sim x \sqrt{m}$
as
$m - u(x,m) \sim x \sqrt{m}$
as
![]() $m \uparrow \infty$
we also deduce that
$m \uparrow \infty$
we also deduce that
To conclude, notice that:
and
So we deduce:
6. Wrapping probability distributions on the circle
In the decomposition (1.14) for an exponentially distributed
![]() $X = \gamma _1/\lambda$
with parameter
$X = \gamma _1/\lambda$
with parameter
![]() $\lambda \gt 0$
; that is
$\lambda \gt 0$
; that is
the Eulerian generating function (1.12) is the probability density of the fractional part
![]() $(\gamma _1/\lambda )^\circ$
at
$(\gamma _1/\lambda )^\circ$
at
![]() $u \in [0,1)$
. In this probabilistic representation of Euler’s exponential generating function (1.3), the factorially normalised Bernoulli polynomials
$u \in [0,1)$
. In this probabilistic representation of Euler’s exponential generating function (1.3), the factorially normalised Bernoulli polynomials
![]() $b_n(u)$
for
$b_n(u)$
for
![]() $n\gt 0$
are the densities at
$n\gt 0$
are the densities at
![]() $u \in [0,1)$
of a sequence of signed measures on
$u \in [0,1)$
of a sequence of signed measures on
![]() $[0,1)$
, each with total mass
$[0,1)$
, each with total mass
![]() $0$
, which when weighted by
$0$
, which when weighted by
![]() $({-}\lambda )^n$
and summed over
$({-}\lambda )^n$
and summed over
![]() $n \gt 0$
give the difference between the probability density of
$n \gt 0$
give the difference between the probability density of
![]() $(\gamma _1/\lambda )^\circ$
and the uniform probability density
$(\gamma _1/\lambda )^\circ$
and the uniform probability density
![]() $b_0(u) \equiv 1$
for
$b_0(u) \equiv 1$
for
![]() $u \in [0,1)$
.
$u \in [0,1)$
.
For a positive integer
![]() $r$
and a positive real number
$r$
and a positive real number
![]() $\lambda$
, let
$\lambda$
, let
![]() $f_{r,\lambda }$
denote the probability density of the gamma(
$f_{r,\lambda }$
denote the probability density of the gamma(
![]() $r,\lambda$
) distribution:
$r,\lambda$
) distribution:
It is well known that
![]() $f_{r,\lambda }$
is the
$f_{r,\lambda }$
is the
![]() $r$
-fold convolution of
$r$
-fold convolution of
![]() $f_{1,\lambda }$
on the real line i.e.
$f_{1,\lambda }$
on the real line i.e.
![]() $f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \ast r}$
.
$f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \ast r}$
.
Let
![]() $\gamma _{r,\lambda }$
be a random variable with distribution gamma(
$\gamma _{r,\lambda }$
be a random variable with distribution gamma(
![]() $r,\lambda$
) and let us denote by
$r,\lambda$
) and let us denote by
![]() $\gamma _{r,\lambda }^\circ$
the random variable
$\gamma _{r,\lambda }^\circ$
the random variable
![]() $\gamma _{r,\lambda } \mod \mathbb{Z}$
on the circle
$\gamma _{r,\lambda } \mod \mathbb{Z}$
on the circle
![]() $\mathbb{T}$
. The probability density of
$\mathbb{T}$
. The probability density of
![]() $\gamma _{r,\lambda }^\circ$
on
$\gamma _{r,\lambda }^\circ$
on
![]() ${\mathbb{T}} = [0,1)$
is given for
${\mathbb{T}} = [0,1)$
is given for
![]() $0 \le u \lt 1$
by
$0 \le u \lt 1$
by
 \begin{equation} f_{\gamma _{r,\lambda }}^\circ (u) = \sum _{m \in \mathbb{Z}}^{} f_{\gamma _{r,\lambda }}(u + m) = \frac{\lambda ^r}{\Gamma (r)} e^{-\lambda u} \sum _{m = 0 }^{\infty } (u+m)^{r-1} e^{-\lambda m} \end{equation}
\begin{equation} f_{\gamma _{r,\lambda }}^\circ (u) = \sum _{m \in \mathbb{Z}}^{} f_{\gamma _{r,\lambda }}(u + m) = \frac{\lambda ^r}{\Gamma (r)} e^{-\lambda u} \sum _{m = 0 }^{\infty } (u+m)^{r-1} e^{-\lambda m} \end{equation}
where
![]() $\Phi$
is the Hurwitz-Lerch zeta function
$\Phi$
is the Hurwitz-Lerch zeta function
![]() $\Phi (z,s,u) = \sum _{m \geq 0} \frac{z^m}{(u + m)^s}$
. In particular, for
$\Phi (z,s,u) = \sum _{m \geq 0} \frac{z^m}{(u + m)^s}$
. In particular, for
![]() $r = 1$
the probability density of
$r = 1$
the probability density of
![]() $\gamma _{1,\lambda }^\circ$
, the fractional part of an exponential variable with mean
$\gamma _{1,\lambda }^\circ$
, the fractional part of an exponential variable with mean
![]() $1/\lambda$
, at
$1/\lambda$
, at
![]() $u \in [0,1)$
, is
$u \in [0,1)$
, is
where
![]() $B(x,\lambda )$
, evaluated here for
$B(x,\lambda )$
, evaluated here for
![]() $x = 1-u$
, is the generating function in (1.3). Combined with the reflection symmetry (1.11), this shows that the probability density of
$x = 1-u$
, is the generating function in (1.3). Combined with the reflection symmetry (1.11), this shows that the probability density of
![]() $\gamma _{1,\lambda }^\circ$
can be expanded in Bernoulli polynomials as:
$\gamma _{1,\lambda }^\circ$
can be expanded in Bernoulli polynomials as:
The following proposition generalises this result to all integers
![]() $r \geq 1$
.
$r \geq 1$
.
The expansion (6.4) can be read from (6.2) and formula (11) on page 30 of [Reference Erdélyi, Magnus, Oberhettinger and Tricomi15]. The consequent interpretation (6.5) of
![]() $b_r(u)$
for
$b_r(u)$
for
![]() $r \gt 0$
, as the density of a signed measure describing how the probability density
$r \gt 0$
, as the density of a signed measure describing how the probability density
![]() $f_{\gamma _{r,\lambda }}^\circ (u)$
approaches the uniform density
$f_{\gamma _{r,\lambda }}^\circ (u)$
approaches the uniform density
![]() $1$
as
$1$
as
![]() $\lambda \downarrow 0$
, dates back to the work of Nörlund [Reference Nörlund32, p. 53], who gave an entirely analytical account of this result. See also [Reference Coelho9] for further study of the wrapped gamma and related probability distributions, and [Reference Dilcher, Straub and Vignat12] for various identities related to (6.4).
$\lambda \downarrow 0$
, dates back to the work of Nörlund [Reference Nörlund32, p. 53], who gave an entirely analytical account of this result. See also [Reference Coelho9] for further study of the wrapped gamma and related probability distributions, and [Reference Dilcher, Straub and Vignat12] for various identities related to (6.4).
Proposition 6.1 (Wrapped gamma distribution). For each
![]() $r = 1,2,3, \ldots$
the wrapped gamma density admits the following expansion:
$r = 1,2,3, \ldots$
the wrapped gamma density admits the following expansion:
where the convergence is uniform in
![]() $u \in [0,1)$
. In particular, as
$u \in [0,1)$
. In particular, as
![]() $\lambda \downarrow 0$
$\lambda \downarrow 0$
Proof. Since
![]() $f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \circledast r}$
we deduce that
$f_{\gamma _{r,\lambda }} = (f_{\gamma _{1,\lambda }})^{ \circledast r}$
we deduce that
![]() $f_{\gamma _{r,\lambda }}^\circ = (f_{\gamma _{1,\lambda }}^\circ )^{\circledast r}$
. Then, combining (6.3) and Corollary 1.2 we deduce that
$f_{\gamma _{r,\lambda }}^\circ = (f_{\gamma _{1,\lambda }}^\circ )^{\circledast r}$
. Then, combining (6.3) and Corollary 1.2 we deduce that
 \begin{align*} f_{\gamma _{r,\lambda }}^\circ (u) &= \left(\underbrace{ f_{\gamma _{1,\lambda }}^\circ \circledast \dots \circledast f_{\gamma _{1,\lambda }}^\circ }_{r \textrm{ factors}}\right)(u)\\[3pt] &= 1 + \sum _{k_1,\dots, k_r \geq 1} ({-}1) ^{k_1 + \dots + k_r}\lambda ^{k_1 + \dots + k_r} \left(b_{k_1} \circledast \dots \circledast b_{k_r}\right)(u)\\[3pt] &= 1 + \sum _{n = r}^{\infty } \sum _{ \substack{ k_1,\dots,k_r \geq 1 \\[3pt] k_1+\dots + k_r = n } }^{} ({-}1)^n \lambda ^n ({-}1)^{-r+1 }b_{n}(u)\\[3pt] &= 1+ \sum _{n = r}^{\infty } ({-}1)^{n-r+1} A_{r,n} \lambda ^n b_{n}(u), \end{align*}
\begin{align*} f_{\gamma _{r,\lambda }}^\circ (u) &= \left(\underbrace{ f_{\gamma _{1,\lambda }}^\circ \circledast \dots \circledast f_{\gamma _{1,\lambda }}^\circ }_{r \textrm{ factors}}\right)(u)\\[3pt] &= 1 + \sum _{k_1,\dots, k_r \geq 1} ({-}1) ^{k_1 + \dots + k_r}\lambda ^{k_1 + \dots + k_r} \left(b_{k_1} \circledast \dots \circledast b_{k_r}\right)(u)\\[3pt] &= 1 + \sum _{n = r}^{\infty } \sum _{ \substack{ k_1,\dots,k_r \geq 1 \\[3pt] k_1+\dots + k_r = n } }^{} ({-}1)^n \lambda ^n ({-}1)^{-r+1 }b_{n}(u)\\[3pt] &= 1+ \sum _{n = r}^{\infty } ({-}1)^{n-r+1} A_{r,n} \lambda ^n b_{n}(u), \end{align*}
where
![]() $A_{r,n} = \binom{n-1}{r-1}$
is the number of
$A_{r,n} = \binom{n-1}{r-1}$
is the number of
![]() $r$
-tuples of positive integers that sum to
$r$
-tuples of positive integers that sum to
![]() $n$
. Notice that all the sums we considered are summable uniformly in
$n$
. Notice that all the sums we considered are summable uniformly in
![]() $u \in [0,1]$
since
$u \in [0,1]$
since
![]() $\left \lVert b_n\right \rVert _\infty = O((2\pi )^n)$
as
$\left \lVert b_n\right \rVert _\infty = O((2\pi )^n)$
as
![]() $n \to \infty$
, see (1.7).
$n \to \infty$
, see (1.7).
Remark 6.2. The general problem of expanding a function on
![]() $\mathbb{T}$
as a sum of Bernoulli polynomials was first treated Jordan [Reference Jordan21, Section 85] and Mordell [Reference Mordell31]. In our context, we think of the expansion of a function in Bernoulli polynomials as an analogue of the Taylor expansion where we work with the convolutions
$\mathbb{T}$
as a sum of Bernoulli polynomials was first treated Jordan [Reference Jordan21, Section 85] and Mordell [Reference Mordell31]. In our context, we think of the expansion of a function in Bernoulli polynomials as an analogue of the Taylor expansion where we work with the convolutions
![]() $\circledast$
instead of the usual multiplication of functions; i.e. we view expansions of the form
$\circledast$
instead of the usual multiplication of functions; i.e. we view expansions of the form
as an analogue of Taylor expansions
As we have seen in this section, this point of view is especially fruitful when one wishes to convolve probability measures on
![]() ${\mathbb{T}} = [0,1)$
. If
${\mathbb{T}} = [0,1)$
. If
![]() $f$
is a
$f$
is a
![]() $C^\infty$
function on
$C^\infty$
function on
![]() $[0,1]$
satisfying some dominance condition (see [Reference Mordell31, Theorem 1]), the coefficient of
$[0,1]$
satisfying some dominance condition (see [Reference Mordell31, Theorem 1]), the coefficient of
![]() $b_1^{\circledast }(x)$
in the expansion of
$b_1^{\circledast }(x)$
in the expansion of
![]() $f$
is given by
$f$
is given by
Appendix A: An elementary combinatorial proof of Theorem 1.1
As promised in Remark 2.4, we give an elementary combinatorial proof of Theorem 1.1 using generating functions. We first recall the following identity of the Bernoulli numbers
![]() $B_n$
:
$B_n$
:
 \begin{equation} B_{n} = \frac{-1}{n + 1} \sum _{k = 0}^{n-1} \binom{n+1}{k} B_{k}, \quad \text{for }n \geq 1. \end{equation}
\begin{equation} B_{n} = \frac{-1}{n + 1} \sum _{k = 0}^{n-1} \binom{n+1}{k} B_{k}, \quad \text{for }n \geq 1. \end{equation}
Proof of Theorem 1.1. We proceed by induction. The first two polynomials
![]() $B_0(x)$
and
$B_0(x)$
and
![]() ${B_1}(x)$
obviously satisfy Theorem 1.1. For
${B_1}(x)$
obviously satisfy Theorem 1.1. For
![]() $n \geq 1$
, assume that
$n \geq 1$
, assume that
![]() ${B_n}(x) = ({-}1)^{n-1} n ! \ \underbrace{{B_1(x)} \circledast \dots \circledast{B_1(x)}}_{n \ \textrm{ factors}}$
. We want to show that
${B_n}(x) = ({-}1)^{n-1} n ! \ \underbrace{{B_1(x)} \circledast \dots \circledast{B_1(x)}}_{n \ \textrm{ factors}}$
. We want to show that
For this, we use Proposition 2.3 to compute
![]() ${B_1} \circledast{B_n}$
as follows:
${B_1} \circledast{B_n}$
as follows:
 \begin{align*}{x} \circledast{B_n}(x) &= x \circledast \sum _{k=0}^{n} \binom{n}{k} B_{n-k} x^{k} \\[3pt] &= B_n \ x \circledast{1} + \sum _{k = 1}^{n} \binom{n}{k} B_{n-k}{x} \circledast{x^k}\\[3pt] &= \frac{B_n}{2} + \sum _{k = 1}^{n} \binom{n}{k} B_{n-k} \left ( \frac{x - x^{k+1}}{k+1} + \frac{1}{(k+1)(k+2)}\right )\\[3pt] &=\sum _{k = 1}^{n} \binom{n}{k} B_{n-k} \frac{x - x^{k+1}}{k+1} + \sum _{k = 0}^{n} \frac{\binom{n}{k} B_{n-k}}{(k+1)(k+2)}, \end{align*}
\begin{align*}{x} \circledast{B_n}(x) &= x \circledast \sum _{k=0}^{n} \binom{n}{k} B_{n-k} x^{k} \\[3pt] &= B_n \ x \circledast{1} + \sum _{k = 1}^{n} \binom{n}{k} B_{n-k}{x} \circledast{x^k}\\[3pt] &= \frac{B_n}{2} + \sum _{k = 1}^{n} \binom{n}{k} B_{n-k} \left ( \frac{x - x^{k+1}}{k+1} + \frac{1}{(k+1)(k+2)}\right )\\[3pt] &=\sum _{k = 1}^{n} \binom{n}{k} B_{n-k} \frac{x - x^{k+1}}{k+1} + \sum _{k = 0}^{n} \frac{\binom{n}{k} B_{n-k}}{(k+1)(k+2)}, \end{align*}
and since
![]() $n \geq 1$
we have
$n \geq 1$
we have
![]() $1 \circledast B_n(x) = 0$
. Given that
$1 \circledast B_n(x) = 0$
. Given that
![]() $B_1(x) = x - 1/2$
, we have
$B_1(x) = x - 1/2$
, we have
 \begin{equation} (n+1){B_1(x)} \circledast{B_n(x)} = \sum _{k = 1}^{n} (n+1) \binom{n}{k} B_{n-k} \frac{x - x^{k+1}}{k+1} + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}. \end{equation}
\begin{equation} (n+1){B_1(x)} \circledast{B_n(x)} = \sum _{k = 1}^{n} (n+1) \binom{n}{k} B_{n-k} \frac{x - x^{k+1}}{k+1} + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}. \end{equation}
We now expand the latter polynomial to match the expansion of
![]() $B_{n+1}(x) = \sum _{k=0}^{n+1} \binom{n+1}{k} B_{n + 1 - k} x^{k}$
. From (A.2) we deduce that
$B_{n+1}(x) = \sum _{k=0}^{n+1} \binom{n+1}{k} B_{n + 1 - k} x^{k}$
. From (A.2) we deduce that
 \begin{align*} (n+1) {B_1}(x) \circledast {B_n}(x) & = - \sum \limits _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} x^k + \left ( \sum \limits _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} \right ) x\\[4pt]& + \sum _{k = 0}^{n} \binom {n}{k} \frac { (n+1) B_{n-k}}{(k+1)(k+2)}. \end{align*}
\begin{align*} (n+1) {B_1}(x) \circledast {B_n}(x) & = - \sum \limits _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} x^k + \left ( \sum \limits _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} \right ) x\\[4pt]& + \sum _{k = 0}^{n} \binom {n}{k} \frac { (n+1) B_{n-k}}{(k+1)(k+2)}. \end{align*}
Notice that, thanks to the recursion Equation (A.1), the coefficient of
![]() $x$
in the polynomial
$x$
in the polynomial
![]() $(n+1)x \circledast B_n(x)$
is
$(n+1)x \circledast B_n(x)$
is
 \begin{equation*} \sum _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} = \sum _{k = 0}^{n-1} \binom {n+1}{k} B_{k} = - (n+1) B_n. \end{equation*}
\begin{equation*} \sum _{k = 2}^{n+1} \binom {n+1}{k} B_{n+1-k} = \sum _{k = 0}^{n-1} \binom {n+1}{k} B_{k} = - (n+1) B_n. \end{equation*}
So we deduce that
 \begin{align*} (n+1)({B_1} \circledast{B_n})(x) &= - \sum _{k = 2}^{n+1} \binom{n+1}{k} B_{n+1-k} x^k - (n+1) B_n x + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}\\[3pt] & = - \sum _{k = 1}^{n+1} \binom{n+1}{k} B_{n+1-k} x^k + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}. \end{align*}
\begin{align*} (n+1)({B_1} \circledast{B_n})(x) &= - \sum _{k = 2}^{n+1} \binom{n+1}{k} B_{n+1-k} x^k - (n+1) B_n x + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}\\[3pt] & = - \sum _{k = 1}^{n+1} \binom{n+1}{k} B_{n+1-k} x^k + \sum _{k = 0}^{n} \binom{n}{k} \frac{ (n+1) B_{n-k}}{(k+1)(k+2)}. \end{align*}
All that remains is to deal with the constant coefficient in (A.2), and from Lemma A.1 we can see that the constant coefficient in the polynomial
![]() $(n+1)({B_1} \circledast{B_n})(x)$
is
$(n+1)({B_1} \circledast{B_n})(x)$
is
Hence, we obtain the desired equation
 \begin{equation*} (n+1)( {B_1} \circledast {B_n})(x) = - \sum _{k = 0}^{n+1} \binom {n+1}{k} B_{n+1-k} x^k = - {B_{n+1}}(x), \end{equation*}
\begin{equation*} (n+1)( {B_1} \circledast {B_n})(x) = - \sum _{k = 0}^{n+1} \binom {n+1}{k} B_{n+1-k} x^k = - {B_{n+1}}(x), \end{equation*}
where the last equality is deduced from to (A.1).
Lemma A.1.
For any integer
![]() $n \geq 0$
the following equation holds:
$n \geq 0$
the following equation holds:
Proof. The generating function of the sequence
![]() $\left (\frac{1}{(n+2)!}\right )_{n \geq 0}$
is the function
$\left (\frac{1}{(n+2)!}\right )_{n \geq 0}$
is the function
and the generating function of the sequence
![]() $\left (\frac{B_n}{n!}\right )_{n \geq 0}$
is
$\left (\frac{B_n}{n!}\right )_{n \geq 0}$
is
![]() $B(0,z) \,:\!=\, \sum _{n \geq 0} \frac{B_n}{n!} z^n = \frac{z}{e^z - 1}$
. So the generating function of the convolution of the two sequences is
$B(0,z) \,:\!=\, \sum _{n \geq 0} \frac{B_n}{n!} z^n = \frac{z}{e^z - 1}$
. So the generating function of the convolution of the two sequences is
 \begin{equation*} h(z) \,:\!=\, g(z)B(0, z) = \sum _{n=0}^{\infty } \left ( \sum _{k = 0}^{n} \frac {1}{(k+2)!} \frac {B_{n-k}}{(n-k)!} \right ) z^n = \frac {e^z - z - 1}{ z (e^z - 1)}. \end{equation*}
\begin{equation*} h(z) \,:\!=\, g(z)B(0, z) = \sum _{n=0}^{\infty } \left ( \sum _{k = 0}^{n} \frac {1}{(k+2)!} \frac {B_{n-k}}{(n-k)!} \right ) z^n = \frac {e^z - z - 1}{ z (e^z - 1)}. \end{equation*}
Now, the generating function of the sequence
![]() $\left ( \frac{B_{n+1}}{(n+1)!} \right )_{n\geq 0}$
is
$\left ( \frac{B_{n+1}}{(n+1)!} \right )_{n\geq 0}$
is
We deduce that
![]() $h(z) = - f(z)$
hence the desired result.
$h(z) = - f(z)$
hence the desired result.
Appendix B: Complement to the proof of Proposition 5.13
Here we check that the array
![]() $Y_{k,m} = (m X_k^{(m)} - 1)/ \sqrt{m}$
where
$Y_{k,m} = (m X_k^{(m)} - 1)/ \sqrt{m}$
where
![]() $X_{1}^{(m)}, X_{2}^{(m)}, \dots$
is a sequence of i.i.d beta(
$X_{1}^{(m)}, X_{2}^{(m)}, \dots$
is a sequence of i.i.d beta(
![]() $1, m$
) random variables, satisfies the conditions required in the Lindeberg-Feller theorem [Reference Durrett13, Theorem 3.4.10]. For that we need to check the following:
$1, m$
) random variables, satisfies the conditions required in the Lindeberg-Feller theorem [Reference Durrett13, Theorem 3.4.10]. For that we need to check the following:
-
1.
 $\sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2] \xrightarrow []{m \to \infty } 1$
.
$\sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2] \xrightarrow []{m \to \infty } 1$
. -
2. For any
 $\epsilon \gt 0$
, we have
$\epsilon \gt 0$
, we have
 $\sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] \xrightarrow []{m \to \infty } 0$
.
$\sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] \xrightarrow []{m \to \infty } 0$
.
For the first condition we have
For the second condition, fix
![]() $\epsilon \gt 0$
and note that the density of
$\epsilon \gt 0$
and note that the density of
![]() $Y_{k,m}$
is
$Y_{k,m}$
is
So for large enough
![]() $m$
we get
$m$
we get
 \begin{align*} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \int _{-1/\sqrt{m}}^{(m-1)/\sqrt{m}} y^2 g_m(y) \ 1[|y|\gt \epsilon ] dy \\[3pt] &= \int _{\epsilon }^{(m-1)/\sqrt{m}} y^2 g_m(y) dy \\[3pt] &= \sqrt{m} \int _{\epsilon }^{(m-1)/\sqrt{m}} y^2 \left ( 1 - \frac{\sqrt{m} \ y +1 }{m} \right )^{m-1} dy. \\[3pt] \end{align*}
\begin{align*} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \int _{-1/\sqrt{m}}^{(m-1)/\sqrt{m}} y^2 g_m(y) \ 1[|y|\gt \epsilon ] dy \\[3pt] &= \int _{\epsilon }^{(m-1)/\sqrt{m}} y^2 g_m(y) dy \\[3pt] &= \sqrt{m} \int _{\epsilon }^{(m-1)/\sqrt{m}} y^2 \left ( 1 - \frac{\sqrt{m} \ y +1 }{m} \right )^{m-1} dy. \\[3pt] \end{align*}
With the change of variable
![]() $z = (\sqrt{m}y + 1)/ m$
we get
$z = (\sqrt{m}y + 1)/ m$
we get
 \begin{align*} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \int _{(\epsilon \sqrt{m} +1)/m}^{1} (mz - 1)^2 (1-z)^{m-1} dz\\[3pt] &= \left (1 - \frac{\epsilon \sqrt{m} + 1}{m} \right )^m \frac{m( \epsilon ^2 m (m+1) + 2m + 2 \epsilon \sqrt{m}(m-1) - 4 ) + 2 }{m(m+1)(m+2)}. \end{align*}
\begin{align*} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \int _{(\epsilon \sqrt{m} +1)/m}^{1} (mz - 1)^2 (1-z)^{m-1} dz\\[3pt] &= \left (1 - \frac{\epsilon \sqrt{m} + 1}{m} \right )^m \frac{m( \epsilon ^2 m (m+1) + 2m + 2 \epsilon \sqrt{m}(m-1) - 4 ) + 2 }{m(m+1)(m+2)}. \end{align*}
So we deduce that
 \begin{align*} \sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \left (1 - \frac{\epsilon \sqrt{m} + 1}{m} \right )^m \frac{m( \epsilon ^2 m (m+1) + 2m + 2 \epsilon \sqrt{m}(m-1) - 4 ) + 2 }{(m+1)(m+2)} \\[3pt] & \substack{\simeq \\[3pt] m \to \infty } \ \epsilon ^2 m e^{-\epsilon \sqrt{m}}. \end{align*}
\begin{align*} \sum _{k=1}^{m} \mathbb{E}[Y_{k,m}^2;\, |Y_{k,m}| \gt \epsilon ] &= \left (1 - \frac{\epsilon \sqrt{m} + 1}{m} \right )^m \frac{m( \epsilon ^2 m (m+1) + 2m + 2 \epsilon \sqrt{m}(m-1) - 4 ) + 2 }{(m+1)(m+2)} \\[3pt] & \substack{\simeq \\[3pt] m \to \infty } \ \epsilon ^2 m e^{-\epsilon \sqrt{m}}. \end{align*}
So we deduce that