Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goldwasser, John
and
Hansen, Ryan
2013.
The Exact Turán Number of $F(3,3)$ and All Extremal Configurations.
SIAM Journal on Discrete Mathematics,
Vol. 27,
Issue. 2,
p.
910.
Hefetz, Dan
and
Keevash, Peter
2013.
A hypergraph Turán theorem via lagrangians of intersecting families.
Journal of Combinatorial Theory, Series A,
Vol. 120,
Issue. 8,
p.
2020.
FALGAS-RAVRY, VICTOR
and
VAUGHAN, EMIL R.
2013.
Applications of the Semi-Definite Method to the Turán Density Problem for 3-Graphs.
Combinatorics, Probability and Computing,
Vol. 22,
Issue. 1,
p.
21.
Bellmann, Louis
and
Reiher, Christian
2019.
Turán’s Theorem for the Fano Plane.
Combinatorica,
Vol. 39,
Issue. 5,
p.
961.
Balogh, József
Clemen, Felix Christian
and
Lidický, Bernard
2022.
Solving Turán's tetrahedron problem for the ℓ2$\ell _2$‐norm.
Journal of the London Mathematical Society,
Vol. 106,
Issue. 1,
p.
60.
Chang, An
and
Gao, Guo-rong
2023.
On the Turán Density of Uniform Hypergraphs.
Acta Mathematicae Applicatae Sinica, English Series,
Vol. 39,
Issue. 3,
p.
638.


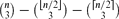 . This sharpens results of Zhou [9] and of the second author and Rödl [7].
. This sharpens results of Zhou [9] and of the second author and Rödl [7].